一道联合协作体高考模拟最值题的破解及拓展

⦿安徽省蒙城县第二中学 丁云婷

1 引言

关于一些多参数(至少三个及以上)的代数式的最值问题，往往涉及轮换式，参数众多，抓住代数式的特征，从一个角度切入，从轮换式的特征进行合理对称处理，利用不等式特征，合理构建数学模型，有效破解最值问题．

2 问题呈现

3 问题剖析

此题是一道关于多参数的不等式问题，结合多参数的分式之和为定值给出对应的条件，进而确定多参数之积的最值问题，主要考查学生推理论证能力，运算求解能力，转化与化归思想，突出逻辑推理、数学运算等核心素养．

其实，确定此类不等式的最值问题的核心就是取“等号”的条件，解决小题(选择题或填空题)时，一般可以借助“先猜后证”的思维方式来处理，根据对称性和猜测确定取“等号”的条件为a1=a2=…=a2 020=4 038，进而再进行分析与处理．

取“等号”的条件确定多参数的最值问题只是一种特殊的思想方法，要根据相应参数之间的等价或轮换条件来合理取“等号”，对于不具有等价或轮换条件时，盲目取“等号”会直接导致错误．取“等号”要谨慎合理，进一步的验证与推理是保证正确性的唯一方式，也是进一步提升准确率的基本步骤．

4 问题破解

方法1：均值不等式法.

解析：由题可得

同理可得

将以上2 020个不等式同向累乘，可得

解得a1a2…a2 020≥4 0382 020，当且仅当a1=a2=…=a2 020=4 038时等号成立.

故填答案：4 0382 020．

点评:结合多参数条件关系式对其中一个参数移项进行变形处理，利用均值不等式进行合理放缩，同理对其他参数进行一样的放缩处理，结合相应不等式的同向累乘，进行变形转化，得以确定对应代数式的最值问题．利用均值不等式法加以处理，直接有效，也是处理此类问题最为常见的基本思维方法．

方法2：代数换元法.

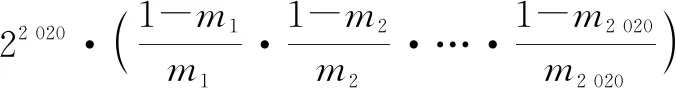
根据均值不等式，可得

对以上2 020个不等式同向累乘，可得

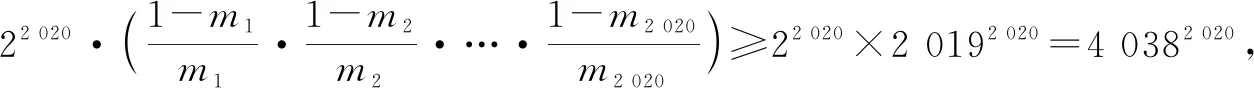
故填答案：4 0382 020．

点评:结合多参数条件关系式的恒等变形，通过代数换元处理，对原问题进行熟知化转化与处理，结合均值不等式进行合理放缩，结合相应不等式的同向累乘，利用所转化的新问题，得以确定对应代数式的最值问题．代数换元处理，将问题熟知化处理，是处理一些创新、陌生问题中比较常用的技巧方法．

方法3：三角换元法.

那么a1a2…a2 020

=22 020(tan2θ1·tan2θ2·…·tan2θ2 020)

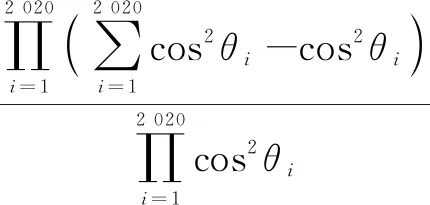
=22 020·2 0192 020

=4 0382 020.

当且仅当cos2θ1=cos2θ2=…=cos2θ2020，即a1=a2=…=a2 020=4 038时等号成立.

故填答案：4 0382 020．

点评:结合多参数条件关系式的恒等变形，通过三角换元处理，对原问题转化为三角函数问题来分析与处理，结合均值不等式对三角关系式进行合理放缩，进而得以确定对应代数式的最值问题．三角换元处理，是破解最值问题中的一种常见技巧，也为问题的进一步推广与拓展具有一定的参考与应用价值．

5 变式拓展

探究1：保留原来的问题背景，结合破解问题的三角换元法处理的应用与归纳，将问题进行一般化升华与提升，变特定常数为更一般的常数，化特殊为一般，得到以下相应的变式问题．

具体破解过程可以参考以上问题中的相关方法，得到对应的答案：mn(n-1)n．具体的破解方法与过程直接参考以上问题的破解过程即可．特别当m=2，n=2 020时，就是原来的问题，对应代数式的最小值就是mn(n-1)n=22 020×(2 020-1)2 020=4 0382 020．

特别地，在变式1的背景中，取常数m=1，是以上问题的一个特例，可得到一个比较常见的最值问题.

对应答案为：(n-1)n．这就是一个比较常规的数学问题，往往以n=3或是相近的数字形式出现，在一些竞赛题中有其影子．

6 教学启示

此类涉及多参数代数式且与不等式有关的最值问题，创新新颖，变化多端，难度适中，解法多样，是高考或联赛中比较常见的重点与难点，主要考查学生综合运用不等式思想解决问题的能力．

6.1 借助不等式思维切入

抓住多参数的轮换变化规律，结合已知条件中的多参数代数式的特征，通过代数式的恒等变换与巧妙运算，结合不等式思维，特别是基本不等式、均值不等式以及一些不等式的基本性质等加以合理应用．

6.2 建立熟知数学模型

对于一些比较陌生或创新的数学问题，经常可以利用换元处理等思维方式，化陌生为熟知，借助已有熟知的数学模型加以分析或处理．这种转换过程就是一个对问题重新加工、理解与应用的过程，也是已有数学模型的应用．从而更加有效地形成良好的数学品质，提高数学能力，培养数学核心素养．Z