基于随机森林的水质监测指标预测
李旭杰,史 灵,花思洋,孙 颖,黄凤辰
(1.河海大学海洋与近海工程研究院,江苏 南通 226300;2.河海大学计算机与信息学院,江苏 南京 210098;3.钛能科技股份有限公司,江苏 南京 211806;4.江苏开放大学信息工程学院,江苏 南京 210017)
1 概 述
本文以江苏省南京市秦淮新河为代表站进行研究。秦淮新河属秦淮河水系,起于河定桥经西善桥至金胜村入江口,总长16.8 km,是下游入江分洪道的一条重要通道[1]。选取2020年6月至2021年6月的水质监测各类监测指标数据,利用Pearson相关系数对指标间进行相关性分析,得到各监测指标间的相关系数,对变量关系间的强弱进行有效度量,对影响水质的主导因素进行识别,然后采用多元线性回归算法进一步分析水质指标间的统计关系[2],确定变量之间的因果关系,并对多元线性回归算法的可信程度进行检验。根据符合评价标准的多元回归方程,通过随机森林模型用自变量指标对因变量指标做出进一步预测,若之后监测到的水质指标值与预测值相比有较大差异,则可以说明该河段水质有较大变化,可起到预警作用[3],能够对水质可能出现的问题进行有效预防,构建一个高效的水质监测预测模型,能够为秦淮新河的水环境保护提供科学指导依据。
2 国内外研究现状
传统的水质监测一般是进行人工操作,这种监测方法不能及时、准确地获得水质不断变化的动态数据。而通过各类监测水质指标的传感器实现对水体中的COD、NH3-N、pH值等进行在线精确监测,能有效提升水质监测效率,避免手工测定的耗时费力甚至不精确的一系列缺陷,结合计算机以及通信等技术手段,可以对所采集到的数据进行分析处理,为进一步产生和研究数据奠定基础。
2017年,郑德论[4]通过监测汕头湖沟中上游河段水体的水质状况,采用单因子评价方法确定该河段水体的主要污染物。2018年,汤云[5]针对闽江流域的多项水质指标监测数据,利用小波分解、遗传算法改进的BP神经网络方法,分析闽江流域内水质时空分布特征并解析污染源,构建基于小波分解和遗传算法改进的BP 神经网络的水质预测模型。2019年,杨娜等[6]以雄安新区白洋淀水质为研究对象,用灰色聚类分析法并结合变异系数法赋权,对其水质进行分级与评价,为白洋淀的综合治理提供更加客观科学依据。2020年,秦无双等[7]对蓬溪县主要地表水体进行水质现状分析,采用主成分分析法确定了主要污染因子。2021年,国内杨志民[8]针对契爷石水库进行水质监测,采用综合水质评价法和模糊综合评价法对水库水质进行综合评价。
水质自动监测在我国出现的时间较晚,尚处于起步阶段。就现阶段而言,我国水质监测较国外尚存在一定的差距。目前对水质监测数据的自动采集研究比较多,集中在对水质的在线自动监测上,而对于水质监测所采集到的数据进行分析处理的研究还不多,此方面研究有待拓展。本文对水质监测数据进行分析,构建水质监测指标预测模型,提供一定水质监测的科学依据。
3 水质监测指标预测模型构建
构建水质监测指标预测模型体系,采用统计分析方法,包括相关性分析以及多元回归分析,结合随机森林模型,对水质监测指标进行主导性因素指标的相关预测,构建预测模型见图1。对获取水质监测项目监测过程中所用的各类监测指标数据进行清洗,剔除无效、异常数据。无效、异常数据主要指超过各类水质监测指标传感器的测量范围内的异常数据。
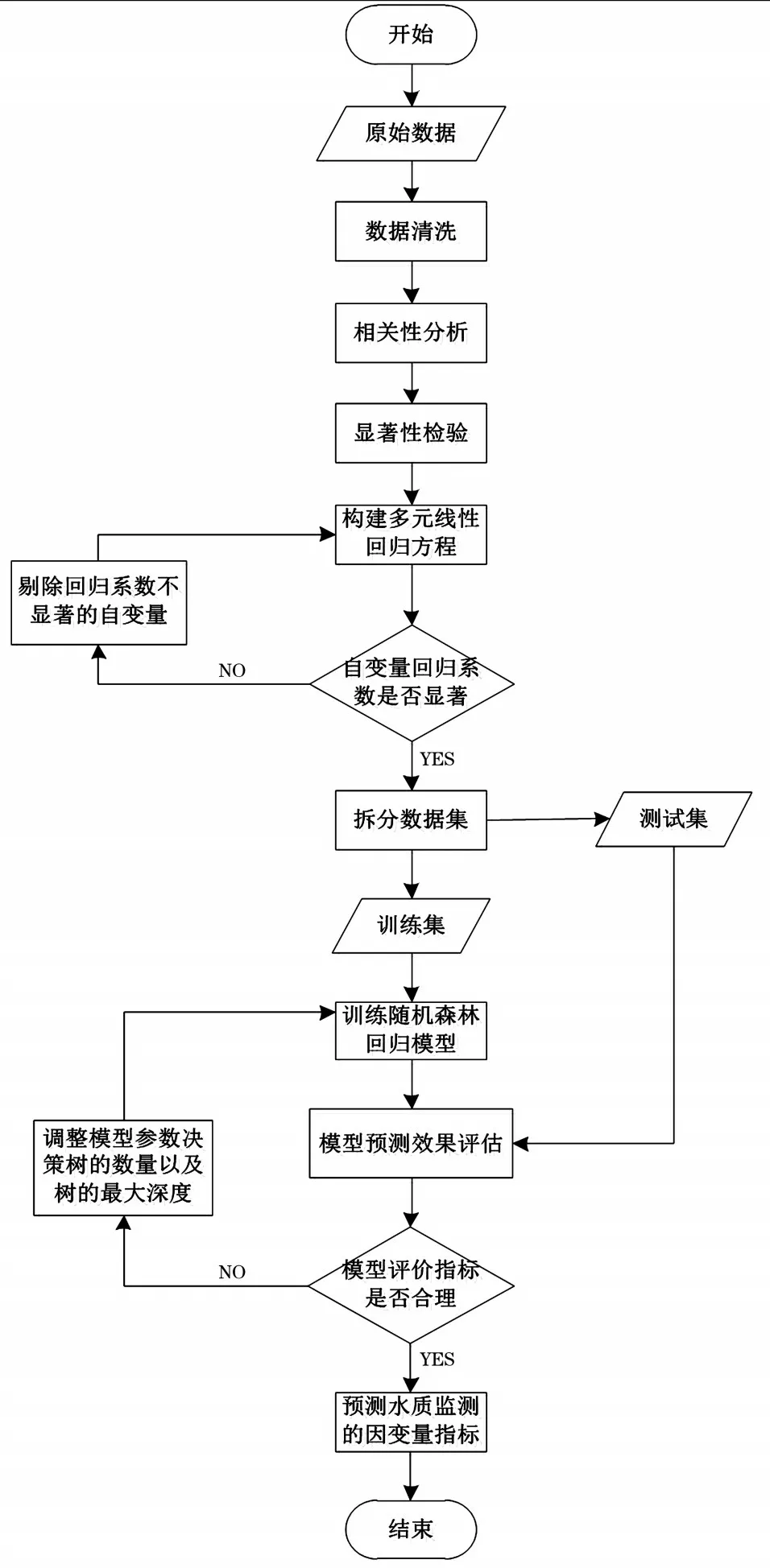
图1 水质监测指标预测模型
3.1 水质监测指标相关性分析
利用相关系数对各类水质监测指标进行相关性分析,常见的相关系数主要有Pearson 相关系数、Spearman 相关系数以及Kendall 秩相关系数,其中Pearson相关系数适用于衡量线性相关关系,针对其适用性,本文采用Pearson相关系数来对6类水质监测指标进行相关程度强弱的度量,定义其公式为
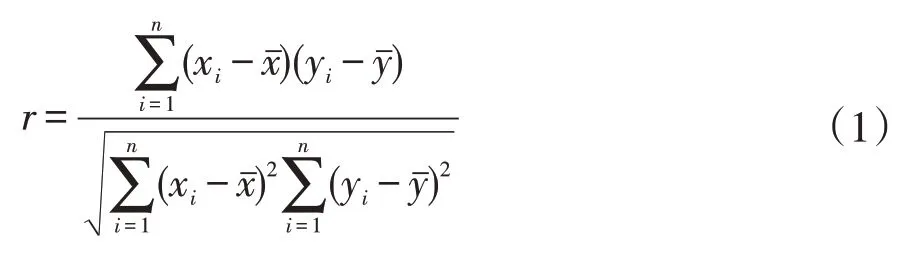
式中:n为样本量;xi和yi分别为2个监测指标的变量值;xˉ和yˉ分别为xi和yi样本的平均值。
图2是6类水质监测指标间Pearson相关系数矩阵热力图,根据热力图颜色的深浅分别可以得到各监测指标间的相关程度强弱。其中,CODcr表示化学需氧量,NH3-N 为氨氮,DO 为溶解氧,WT 为水温,TURB为浊度。
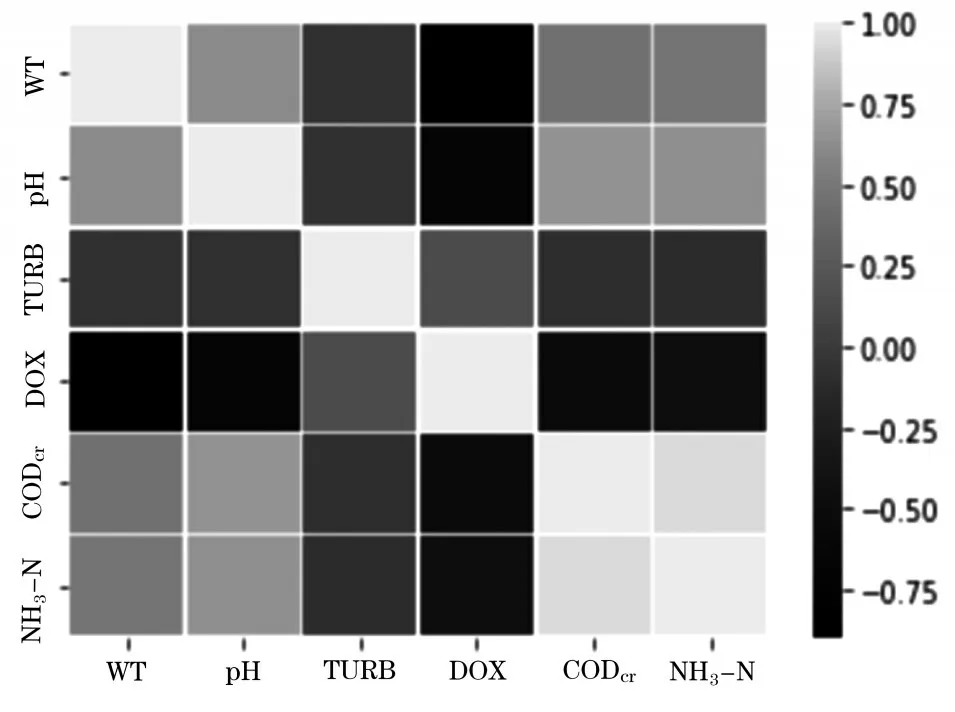
图2 Pearson相关系数矩阵热力
Pearson相关系数矩阵如表1所示。其中,Pearson相关系数的绝对值结果越接近于1表示变量之间的相关性越强,结果越接近于0 表示变量之间的相关性越弱。其绝对值结果在0~0.3 之间,呈现弱相关性;在0.3~0.5之间,呈现低相关性;在0.5~0.8之间,呈现显著相关性;在0.8~1之间,呈现高度相关性[9]。根据表1的分析结果可以得出高度相关的变量有两对,一对是WT 和DO,2 个监测指标间的Pearson 相关系数为-0.8965,明显呈现高度负相关性;另一对是CODcr指标和NH3-N 指标,它们的相关系数为0.9478,明显呈现高度正相关性。

表1 Pearson相关系数矩阵
然后,采用显著性检验的方法对Pearson相关系数进行检验,验证各监测指标间的相关性非偶然因素引起,所得结果能够代表总体指标数据上的相关程度。在本文中,显著性检验的P值均小于选定的显著性水平0.05,故变量之间的相关性都通过显著性检验,显著性检验结果P值列于表2。
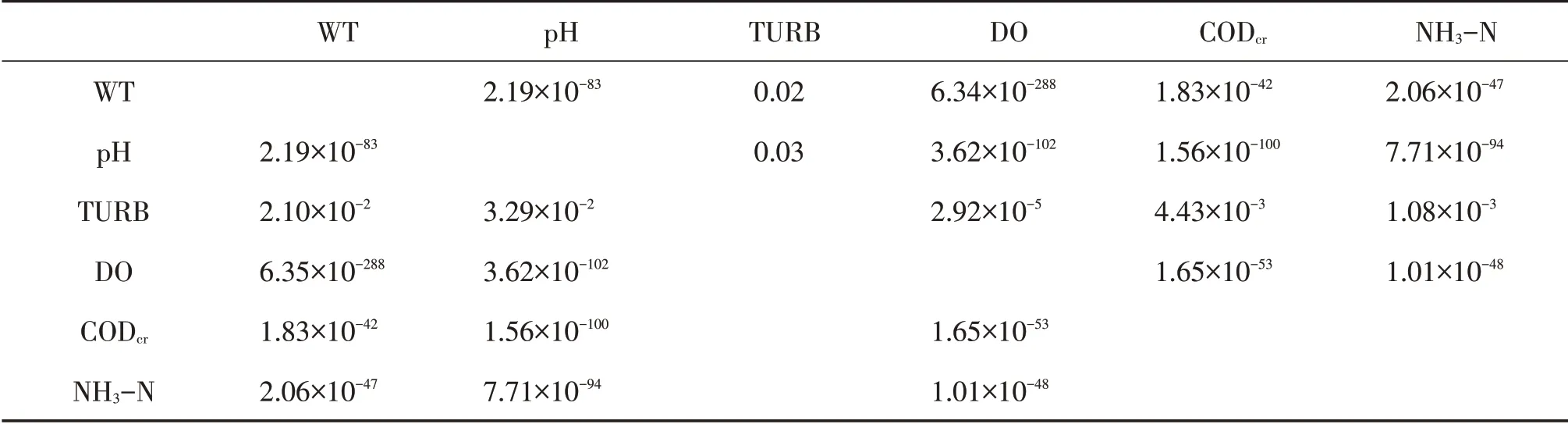
表2 Pearson相关系数显著性检验结果P值
3.2 多元线性回归算法
相关性分析是回归分析的基础和前提,而回归分析则是认识变量间相关程度的具体形式。采用构建多元线性回归方程的方法可进一步得到监测指标间相关程度的具体形式。本文通过回归方程的形式,进一步分析水质指标间的统计关系。
利用多元回归算法,设因变量为y,k个自变量分别为x1,x2,…,xk,描述因变量y如何依赖自变量x1,x2,…,xk和误差项ε的方程。多元线性回归方程可表示如下:
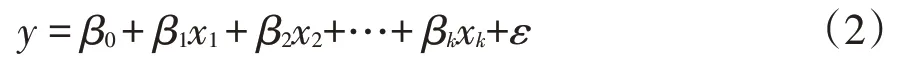
式中:β0,β1,β2,…,βk是模型的参数,ε为误差项,式(2)表明y是x1,x2,…,xk的线性函数加上误差项ε。误差项反映了除x1,x2,…,xk与y的线性关系之外的随机因素对y的影响,是不能由x1,x2,…,xk与y之间的线性关系所解释的变异性[10]。
对得到的多元线性回归方程,剔除回归系数异常以及不显著的自变量,此时的多元线性回归方程可得以成立。回归系数反映的是回归方程中表示自变量x对因变量y影响大小的参数,异常回归系数为回归系数的正负号与Pearson 相关系数相反的数值,不显著的回归系数是指不符合回归系数检验的数值。根据高度相关的变量对可得到2个多元线性回归方程为


3.3 随机森林模型
构建多元线性回归方程后,对整个数据集进行拆分,得到训练集和测试集:训练集用于训练随机森林回归模型,测试集用于模型预测效果的评估。在本文中,取测试集样本数为数据集总样本数的25%。建立随机森林回归模型,采用5 折交叉验证方法利用训练集对模型进行训练。相关参数设置随机值random_state=0,通过5折交叉验证寻找到模型的最佳参数,不重复抽样将原始数据随机分成5份;每次挑选其中1 份作为测试集,剩余4 份作为训练集用作模型训练;重复该步骤5 次,使得每个子集拥有一次作为测试集的机会,其余机会作为训练集;计算5组测试结果的平均值作为模型的准确率[11-12]。
基于上述方法,针对CODcr指标的预测模型可得到决策树的数量n_estimators=50,树的最大深度max_depth=7;针对DO 指标的预测模型得到决策树的数量n_estimators=150,树的最大深度max_depth=6。然后,利用测试集对随机森林回归模型进行预测效果评价,可求得该随机森林回归模型的3 种评价指标的值分别为:均方根误差RMSE=0.2883、平均绝对误差MAE= 0.1813、确定系数R2=0.9831。当随机森林回归模型的确定系数R2已经达到最接近于1,则停止对随机森林回归模型的参数继续调整。根据训练得到的最佳随机森林回归模型,利用水质监测指标中自变量监测指标对因变量指标进行预测。
4 实验结果分析
根据随机森林模型,得到根据水质监测指标中的自变量指标对因变量指标的预测,由水质监测指标的相关性分析以及通过构建多元线性回归方程,得到高度相关的变量对及其因果关系。由训练结果得到相应的随机森林回归模型预测值与水质监测指标中的因变量指标实际值对比图。其中,化学需氧量监测指标实际值与预测值的对比图,见图3,溶解氧监测指标实际值与预测值的对比图,见图4。图3~4 中因变量水质监测指标的实际值为蓝色线,因变量水质监测指标的预测值为黄色线。从图3~4中明显可见因变量水质监测指标的预测值和实际值几乎重合,有效说明本文提出的基于随机森林回归模型的水质监测指标预测方法能够实现因变量水质监测指标的准确预测。
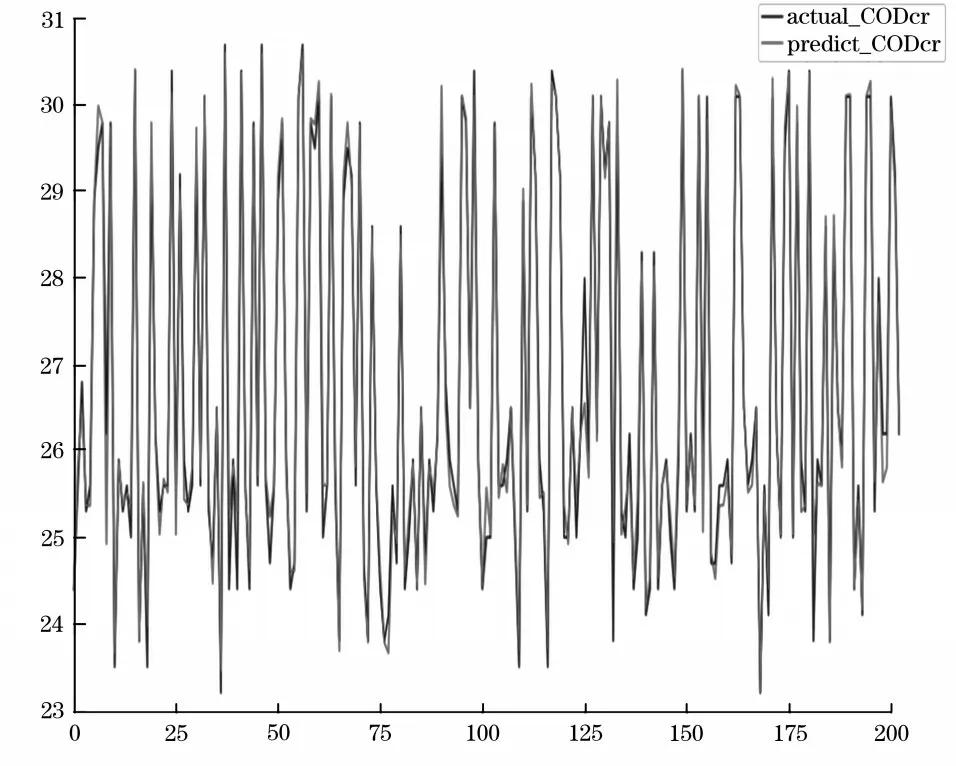
图3 COD监测指标对比
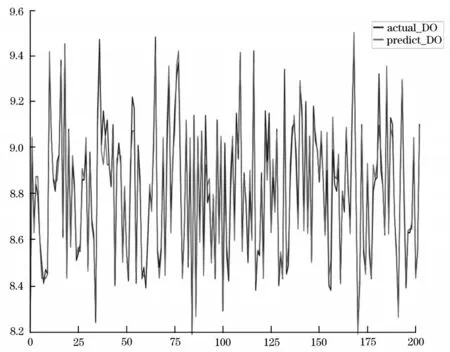
图4 DO监测指标对比
5 结 语
近年来我国水质监测发展迅速,对水质状况进行监测时往往监测的指标种类众多,监测成本较高且信息量巨大,难以从中提取有效信息,对数据进行有效分析势在必行。为有效降低监测成本,对监测指标项目进行合理降维,利用Pearson相关系数对指标间进行相关性分析,对变量关系间的强弱进行有效度量,但由于并未对变量之间的关系进行固化形成模型,无法利用这种关系对数据进行预测,需要进一步进行回归分析,在实际应用中一个参数指标往往受到多个参数指标的影响,多元线性回归算法易于实施,具有较大的应用前景。
在水质监测对各类指标进行监测的实践中,利用多元线性回归得到高度相关的监测指标间统计方程,可以准确得知自变量指标和因变量指标之间的关系,对因变量指标进行有效预测可减低监测成本。利用随机森林模型中的回归模型对监测指标进行预测,相对于其他模型而言,随机森林回归模型具有预测准确度高、泛化能力强的优势。实验结果也能够有效表明随机森林回归模型可利用因变量水质监测指标实现对自变量水质监测指标的准确预测,随机森林回归模型在水质监测指标分析预测的应用研究具有重要意义。

