基于NSST与引导滤波的医学图像融合算法*
石平霞, 陈世国, 丁冬冬
(贵州师范大学 物理与电子科学学院, 贵州 贵阳 550025)
0 引 言
对于获取不同模态的医学图像需要选用不同的成像仪器,不同模态的医学图像也携带着不一样的组织信息。比如计算机断层扫描(computerized tomography,CT)图像和磁共振成像(magnetic resonance imaging,MRI),CT图像可以提供骨骼硬组织的信息,MRI中则是显示了软组织信息;单一模态的图像并不能携带人体组织的全部信息,这对医生的诊断是不利的。为了提高医生对病情诊断的准确性,并制定合理和完善的治疗方案,这需要将不同模态的医学图像中的有用信息在同一图像中呈现出来。正是由于医学临床中存在这种需求,医学图像融合也越来越受到图像处理人员的关注[1]。
图像融合按融合算法来分,一般分为空间域算法和变换域算法[2]。空间域算法只能进行简单的融合处理,其优点是简单,运行时间短,可以抑制人造纹理,缺点是没有考虑时间域与频率域的关系,所以融合图像不仅视觉效果较差,客观评价因子也不理想。变换域算法是对图像进行多尺度变换,并对多尺度变换下的系数进行处理。金字塔变换的融合方法,融合效果从主客观评价来看,均优于空间域算法[3]。但在融合过程中容易产生大量的冗余数据。Ranchin T和Wald L首次提出了基于小波分析的图像融合这一概念[4],降低了数据处理量,但其分解的方向性有限。
李凯等人[5]提出一种基于四元小波变换与Copula模型的融合方法,融合图像清晰,但在边缘处出现信息丢失的现象。Yin H等人[6]通过将源图像作为训练数据获得联合字典,然后使用最大加权多范数融合规则融合图像,但融合图像存在细节信息丢失的问题。而非下采样剪切波变换(non-subsampled shear wave transformation,NSST)不仅具有平移不变性的优点,还有较强的方向选择性。
因此,为了进一步提高融合图像质量,本文提出了基于非下采样剪切波与引导滤波[7,8]相结合的融合方法。用NSST可以获取源图像的更多细节信息;引导滤波器用于图像处理不仅可以增强空间的连续性,避免引入人造纹理[9],而且设计复杂度比较低。
1 本文算法
1.1 NSST
NSST是通过多尺度分解和方向局部化来实现。使用非下采样金字塔滤波器组NSLP实现多尺度分解,使用剪切滤波器SF实现方向局部化。对源图像进行N级分解,得到1个低频分量和N个大小相同但尺度不同高频分量。3级NSST分解过程如图1所示。
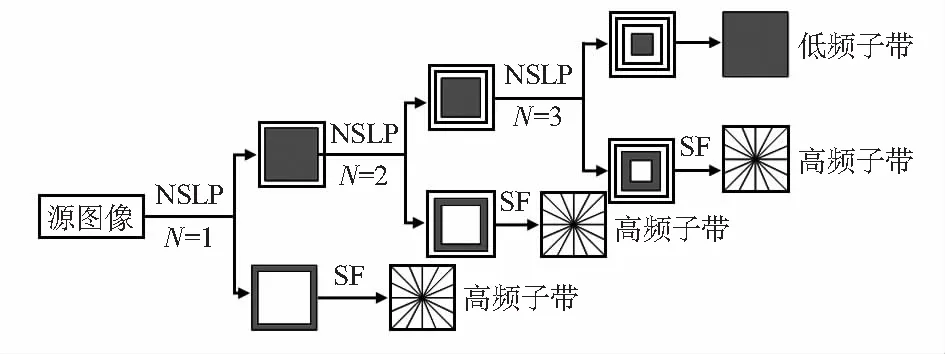
图1 3级NSST分解
1.2 引导滤波
记用于引导的图像为F,输入的图像为I,输出图像为O。输出图像O与引导图像F存在以下的线性关系
Oj=ajFj+bj,∀i∈wi
(1)
式中aj,bj为线性系数,且在窗口wj均为常数。j为窗口wj的中心像素点,wj窗口大小为(2r+1)×(2r+1)。
为确定线性系数aj,bj,则必须对输出图像O有所约束,保证输入图像I和输出图像O之间的差值最小,从而将问题转换为最优求解问题
(2)
式中ε为防止系数aj过大而设定的正则化参数。通过最小二乘法,可以求出线性参数aj和bj
(3)
(4)
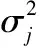
(5)

2 融合规则
2.1 算法流程
对图像进行融合处理时,融合规则是融合处理的核心,它会从运行速度和图像融合的质量两个方面来影响融合处理。因此,选择合适的融合规则在融合处理中具有举足轻重的意义。基于CT和MRI图像融合步骤如下:1)对两幅源图像分别进行NSST分解,得到各自的高低频分量。2)低频部分采用基于引导滤波的加权平均融合方法;高频子带系数采用平均梯度、区域能量指导加权系数和绝对值取大相结合的融合规则。3)对低频子带和高频子带进行NNST逆变换,得到融合图像。本文融合算法流程图如图2所示。
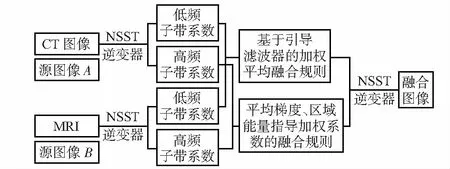
图2 算法流程
2.2 低频融合规则
低频部分包含图像的大部分能量,并且图像中的信息都是存在相关性的,每个像素不是独立的存在,像素在任何位置的像素点都能表现出很强的相关性,因此,不能对低频部分进行简单取最大值或加权平均。但加权平均法有消除部分噪声、源图像信息损失较少的优点。因此,频部分采用基于引导滤波的加权平均融合方法,先将源图像A的低频分量作为引导滤波器的输入图像,源图像B的低频分量作为引导图像。再将源图像B的低频分量作为引导滤波器的输入图像,源图像A的低频分量作为引导图像。即
O=guidedfilter(I,F,r,eps)
(6)
式中O为输出图像,I为输入图像,F为引导图像,r为窗口半径(本文取9)决定引导图像的显著性差异,eps为正则化参数(本文取0.01)决定经过引导滤波的图像模糊度,一般来说,eps越大,图像模糊得越厉害。
用源图像A,B的低频分量分别减去各自的经引导滤波器的输出图像,得到其锐化图像,再根据得到的锐化图像的改进的区域拉普拉斯能量和(SML)来确定融合权值,则融合图像的低频子带系数为
(7)
式中A(i,j)为融合图像在像素点(i,j)的融合系数。wt1和wt2分别为源图像A和B的改进的拉普拉斯能量和
(8)
式中SMLe为第i幅图像的局部区域大小为M×N下的改进的拉普拉斯能量和,本文的区域大小取为3×3。则
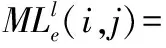
|2Il(i,j)-Il(i,j-p)-Il(i,j+p)|
(9)
2.3 高频融合规则
高频子带系数主要是源图像的轮廓、细节及纹理等信息。人眼的视觉系统对像素不敏感,但对图像的边缘、方向和纹理信息敏感,区域能量保留图像细节信息的同时也反映了图像的相关性。区域能量越大,图像的细节信息也就越丰富。图像的平均梯度反映了图像的清晰度, 同时还反映出图像对微小细节反差的表达能力和图像的纹理变换特征。所以,本文针对高频分量提出区域平均梯度、区域能量和改进的S函数[10]共同指导加权系数的融合规则。
对于高频分量采取如下规则
(10)
式中m,n分别为图像的行和列,f(i,j)为源图像A和B高频分量在像素点(i,j)处的系数值,Tl,k(i,j)为像素点(i,j)处平均梯度,本文中高频子带领域窗口设置为5×5。有
(11)
式中v(i,j)为以像素点(i,j)为中心的大小m×n的邻域窗口,本文中高频子带邻域窗口设置为5×5,El,k(i,j)为像素点(i,j)的局部区域能量。
加权系数w由改进的S函数确定
(12)
式中k为S函数的伸缩因子且大于1,本文取k=5。则高频分量在像素点处(i,j)的高频融合系数
(13)
3 实验结果与分析
3.1 实验环境与图像选取
实验环境:电脑配置为Lenovo XiaoXin I2000,操作系统为Windows7,实验软件为MATLAB。本文选取的是已经经过严格配准的三组CT和MRI图像作为源图像,三组图像大小均为256×256。
3.2 实验结果
将本文算法与基于拉普拉斯金字塔(LP),基于引导滤波(GF),基于自适应稀疏表示的融合(ASR),基于压缩感知融合(SA),基于卷积稀疏的形态成分分析融合(CSMCA)[11],这五种算法进行对比。基于拉普拉斯金字塔算法的分解层数为4,采用加权平均的融合规则,其他算法的。图3(c)、图4(c)、图5(c)为LP融合算法的融合图像,图3(d)、图4(d)、图5(d)为GF融合算法的融合图像,图3(e)、图4(e)、图5(e)为ASR融合算法的融合图像,图3(f)、图4(f)、图5(f)为SA融合算法的融合图像,图3(g)、图4(g)、图5(g)为CSMCA融合算法的融合图像。图3(h)、图4(h)、图5(h)为本文算法的融合图像。融合结果如图3、图4、图5所示。
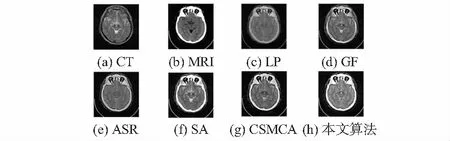
图3 第一组实验结果
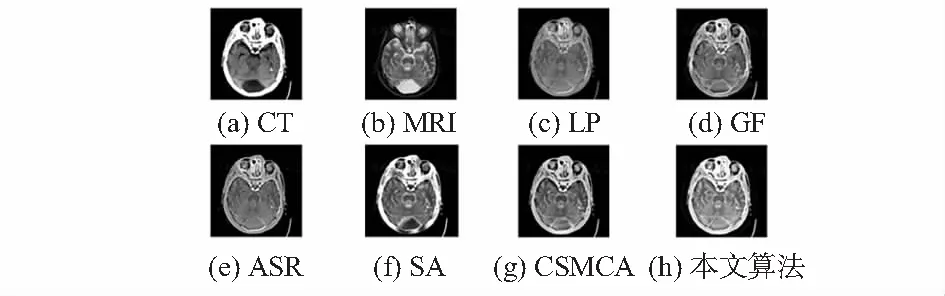
图4 第二组实验结果
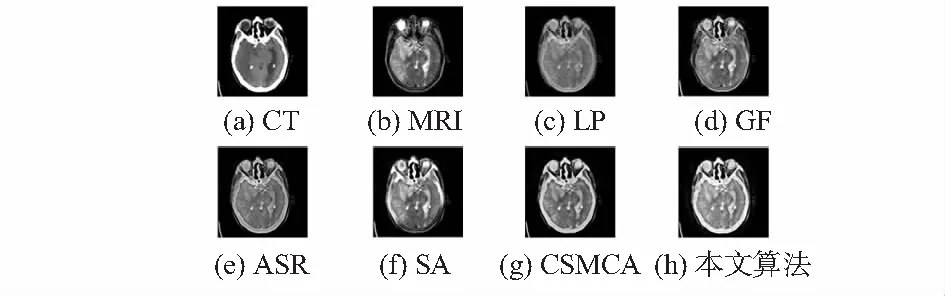
图5 第三组实验结果
3.3 实验分析
从主观评价来看,图3(c)、图3(d)、图3(e)、图3(g)存在图像亮度不足的问题;图3(f)在边缘处出现伪影。图4(c)、图4(d)、图4(e)、图4(f)和图4(g)融合图像较暗,纹理不够清晰;图4(f)在边缘处出现伪影。图5(c)和图5(e)的对比度不强,视觉效果不足;图5(d)和图5(g)的轮廓信息不完整。图3(h)、图4(h)、图5(h)的融合图像中可以看出,融合的图像纹理清晰,细节信息较为丰富,视觉效果较好,为了进一步验证该算法的优越性,本文选取的信息熵(EN)、标准差(STD)、空间频率(SF)、边缘强度(EIN)和图像清晰度(FD)作为图像融合的客观评价标准。评价指标如表1所示。
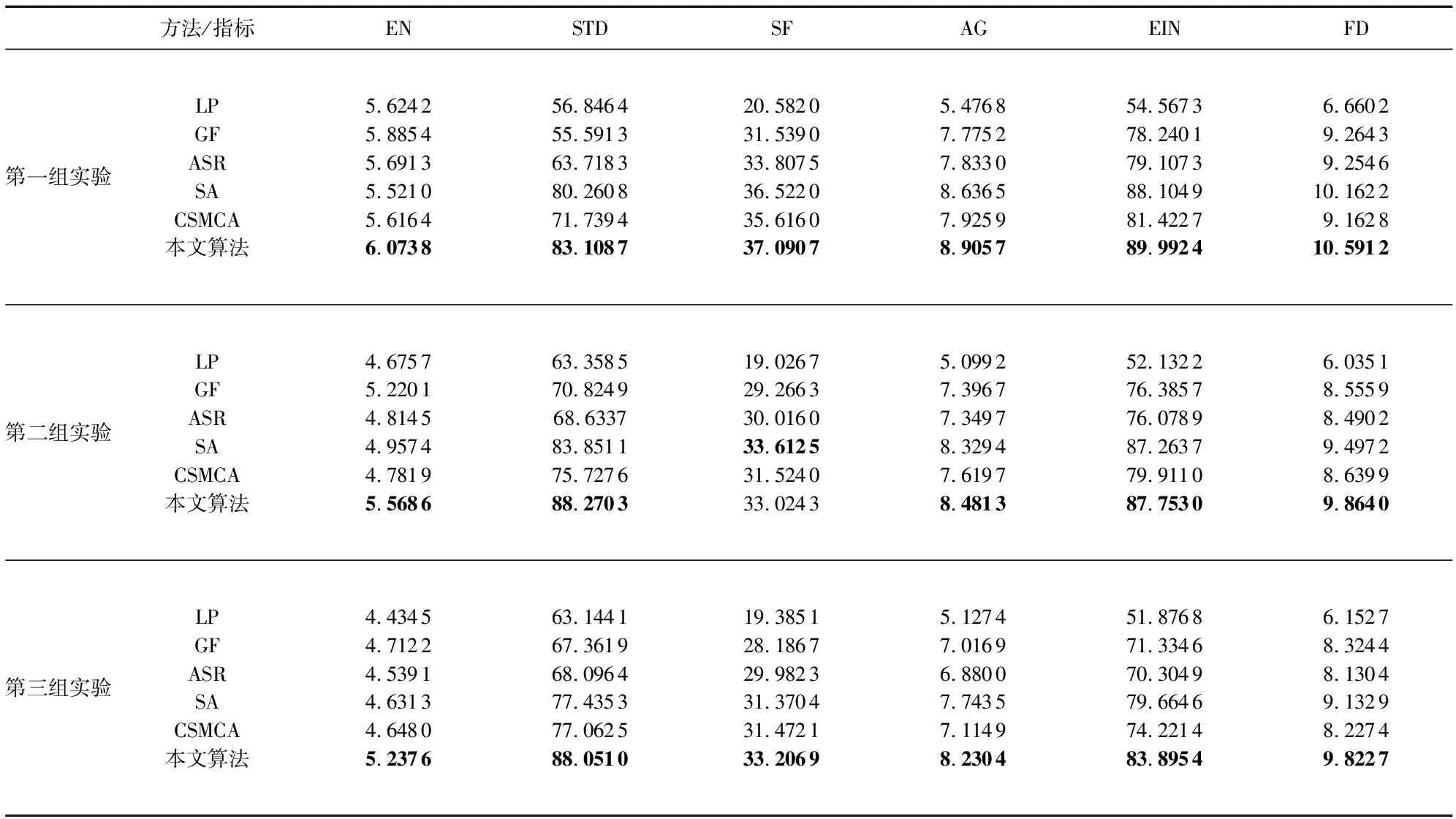
表1 第一组实验客观评价指标表
由表1可知,本文算法在第一组实验和第三组实验中,6个评价指标均优于其他5种算法,本文算法在第二组实验中,仅有空间频率略低于SA算法。
4 结束语
由于医学图像在融合后会存在细节信息不够清晰及信息丢失问题,结合NSST与引导滤波的特性,提出了一种基于NSST与引导滤波相结合的医学图像融合算法。该算法充分利用NSST方向选择性强的特性,结合引导滤波保持边缘特征的优势,对低频部分采用基于引导滤波的加权融合算法,对高频部分采用平均梯度、区域能量指导加权系数的融合策略,很好地完成了CT与MRI图像的融合。实验结果表明:该算法有效的保留了图像的细节信息,提高融合图像的清晰度,避免融合图像的信息丢失。不仅主观上有较好的视觉效果,客观评价中评价指标也有较好的结果,从而说明了该算法是一种较为有效的图像融合算法。

