二维分布式光纤形状传感应变传递研究*
冯雨钦, 王 佩, 刘泽华, 张锦龙
(河南大学 物理与电子学院,河南 开封 475004)
0 引 言
分布式光纤传感技术是利用光在光纤中的散射原理,对沿光纤轴向分布的物体进行连续分布式测量,获得被测物体的应变、温度、空间分布状态的实时监测的技术[1]。由于光纤传感系统具有高精度、高空间分辨率、传感距离远和抗电磁干扰等优点[2,3],近些年来,该项技术在铁路、管道、飞机等大型结构的应力场分布和温度场分布的有效监测有着重要的应用价值[4,5]。由于光纤比较脆弱,在工程应用中需要对光纤进行封装,封装结构材料弹性模量不匹配将导致测量应变与真实应变之间存在传递损失[6]。因此,为提高检测精度,有必要对光纤传感器的应变传递规律进行分析研究。
近年来,国内外学者对光纤传感应变传递规律做了一定的研究。其中,王钰茹等人建立了表贴式光纤—胶结层—基体的模型,得到了应变传递模型中粘贴长度与胶体剪切模量与分布式裸光纤应变传递率的关系[7]。章征林等人建立了光纤—胶结层—基体三层应变传递模型,验证了应变传递模型的准确性和适用性,并得出了涂覆层剪切模量和粘贴长度对传递效果的影响[8]。Li Z X等人建立了嵌入式混凝土应变传递模型,验证了复合模型的可行性,得出了应变传递效率与应变光纤的护套特性和包埋长度的关系[9]。
之前的学者主要研究的是表贴式结构的应变传递率,对无衬底层合式结构研究较少。无衬底层式传感器对比表贴式传感器最重要的区别在于光纤传感器不会固定于某一地方,因此可以用于微创介入手术等场景中。
本文提出一种无衬底层合式结构,并通过建立涂布层—胶结层—传感层三层应变传递耦合理论模型,推导应变传递规律,得到了此结构的应变传递系数k,并分析了各结构参数对应变传递率的影响。
1 应变传递变化分析
1.1 光纤传感特性
光频域反射(optical frequency domain reflection technology,OFDR)技术是基于光纤中瑞利散射原理,通过分析光纤中背向瑞利散射光光谱的变化,继而检测出被测物体应变的变化[10]。
考虑到光纤中存在的瑞利散射效应是在光纤中所有方向上的等概率散射,且在所有散射中散射光强最强,易被检测出。因此,对于应变解调方法通常采用检测光纤中瑞利背向散射光谱变化,从而得到光纤应变变化。
对于特定传感光纤,瑞利背向散射光谱的变化受温度与应变的影响如式(1)所示[11]
Δλ/λ=-Δv/v=kTΔT+kεε
(1)
式中 Δλ为瑞利光波长变化,kT为温度比例系数,kε为应变比例系数。
又因为在纯弯条件下,轴向应变和曲率之间存在式(2)所示关系[12]
(2)
式中ε为光纤轴向检测应变值,ρ为被测物体感测位置曲率半径,κ为相对应的曲率,D为纤芯到中性面距离。通过将式(1)与式(2)相结合,就可对二维形状进行检测与重构。
1.2 建立应力应变传递分析模型
针对层合结构各层之间耦合影响进行分析,提出了图1的传感结构,并对结构应变传递率进行了理论建模与推导。传感器结构由内向外依次是光纤传感层—胶结层—涂布层。此结构有以下两点优势:通过在传感结构中放置两根光纤传感,在检测时将两根光纤所测得的数据取平均,对比传统检测方式可有效地提高测量精度,提高系统的鲁棒性;将传感器上下底面设计为平面,对比传统圆形结构可以更方便地对二维平面做测量,不易松动。

图1 三层传感结构剖面
测量时将底面与被测物体相粘结,当被测物体形状发生变化时,涂布层在外部载荷作用下产生轴向应力,由于模型各层材料的弹性模量不匹配,导致各层之间产生轴向剪应力,涂布层的形变通过轴向剪应力传递到胶结层,胶结层再通过轴向剪应力将形变传导至光纤处,因此,涂布层应变与光纤处应变存在不同,代入基底与光纤之间应变传递率公式,可以检测出各点应变值。
由于传感层采用光纤作为传感器,光纤是一种各向同性材料,为便于对模型进行分析,因此,对模型有以下假设:纤芯与包层机械特性相同,性质变化不大,因此,在分析的过程中可以将两者统一当作玻璃纤维材料分析;轴向外力作用于基材之上,通过胶结层传递到光纤上,胶结层与传感层不直接承受外力作用;涂布层、粘贴层、传感层三层紧密贴合,不发生相对滑移;由于传感器各层结构厚度较薄,因此认为各层截面的轴向应力是均匀的。
1)建立微元段
各层微元应力传递如图2所示。

图2 各层微元应力传递
2)建立各层受力平衡方程并进行受力分析轴向各层受力平衡,光纤微元段力的平衡方程
(3)
粘贴层微元段力的平衡方程
(4)
光纤与粘贴层与涂布层紧密粘结,不发生相对滑移,同步变形,应变变化一致,dεf=dεp。根据材料力学公式可得σ=Eε。由于光纤较细,在发生形变时径向变化较小,可忽略泊松效应及径向位移,因此
(5)
则有在区间[rf,rp]内切应力
(6)
在区间[rp,rm]内切应力
(7)
(8)
由上式可得
(9)
(10)
对x求导可得
(11)
解微分方程可得εf(x)的通解为
(12)
3)结构的应变传递率
(13)
4)平均应变传递率
(14)
式中rf为光纤半径,rp为胶结层最外侧到纤芯距离,rm为涂布层最外侧到纤芯距离,Er为光纤弹性模量,Ep为胶结层弹性模量,Em为涂布层弹性模量,Gp为胶结层剪切模量,Gm为涂布层剪切模量。
2 有限元数值模拟结果分析与验证
2.1 模型参数设置
通过查询相关文献,对所选用的材料特性与结构参数(如表1)做以下假设[13],假设光纤纤芯半径rf为0.125 mm,rp为1 mm,rm为2 mm。

表1 各层结构参数
2.2 传感层应变特性分析
通过以上建立相应的应变传递模型,并对不同长度结构计算得到当L为100,75,50,25,10 mm情况下应变传递率理论变化值,如图3所示。

图3 结构轴向应变传递率理论分布
2.3 应变传递理论与有限元仿真对比
采用Ansys APDL建立三层光纤传感结构的有限元模型,对比验证模型准确度。将这三层结构粘接在一起,假设各层结构相接触的界面都为理想界面。对结构网格划分后如图4所示。

图4 复合材料结构有限元模型
对结构两端的涂布层施加5 MPa的轴向压应力,此复合材料的轴向压应力如图5所示。通过有限元仿真分析得到,从图5(a)中可以清楚地看到,由于剪切滞后效应,在模型的末端形成了一个漏斗状的不均匀变形区域。从图5(b)可以看到,由于不同材料弹性模量不匹配导致各层之间受到的应力不同,应力大小由内向外不断增大,光纤位于应力较小的区域。

图5 复合材料结构数值仿真模拟结果
Ansys结构轴向应变仿真结果如表2。

表2 Ansys结构轴向应变仿真结果
通过表2可见,在模型的末端,被测结构的变形并没有完全传递到光纤上,模型末端的光纤产生的形变变化不如基底明显,光纤不会随着结构的变形而压缩。
将表1中的参数代入到所建立的数学模型中,得到如图6所示的相对误差。分析得出,理论值与仿真值的应变传递率变化趋势是一致的,在中间位置处的应变传递率非常接近,但由于在理论分析过程中对模型的端部做出了无应力传递的假设,并且有限元的分析结果也是近似解,因此,在传感器的两端理论分析值与仿真结果误差较大。

图6 结构轴向应变传递率仿真分布
3 材料结构参数应变率的影响分析
3.1 粘贴层结构对平均应变传递率影响分析
胶结层作为中间层,其物理参数对光纤传感器的应变传递率有重要影响。为尽量减少应变传递率,对胶结层结构参数进行理论分析。胶结层结构参数取值:胶结层厚度为1~5 mm,弹性模量为1~4 GPa,泊松比为0.38~0.5。
3.1.1 胶结层厚度对平均应变传递率影响
当胶结层弹性模量Ep=1 GPa时,分析了胶结层厚度对平均应变传递率的影响效果,从图7可以看出,随着胶结层厚度由1 mm增加至5 mm时,平均应变传递率减小,变化趋势近似直线下降。因此,为保证较高的应变传递率,应缩小胶结层厚度,胶结层厚度取1 mm较为合适。
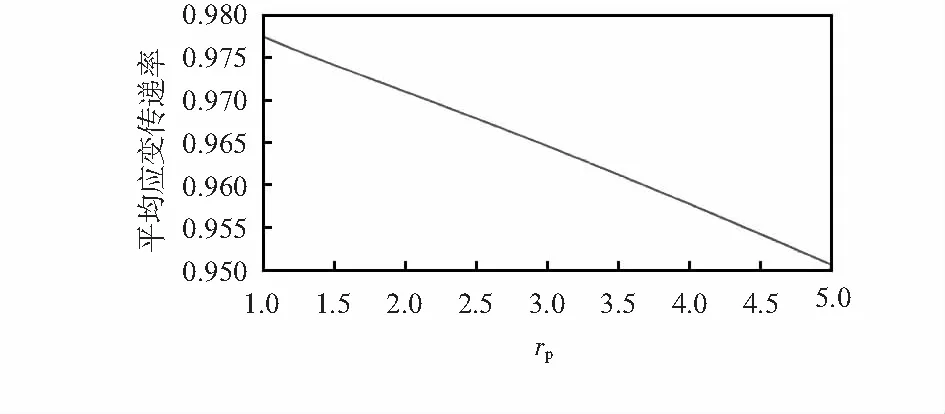
图7 胶结层厚度对平均应变传递率的影响
3.1.2 胶结层弹性模量与泊松比对平均应变传递率影响
图8为胶结层弹性模量与泊松比对平均应变变传递率影响,图中胶结层弹性模量Ep取1~4 GPa,泊松比取0.38~0.5。数据表明,随着胶结层弹性模量的增大,平均应变传递率增大,变化趋势近似直线上升。因此,胶结层选取较高弹性模量、硬度较小的材料可以有效地提高结构的应变传递率,减小传递率的损耗。随着胶结层泊松比的增大,平均应变传递率减小,变化趋势近似直线,但减小的幅度有限,应变传递率变化仅在0.005以内,所以实际应用中可忽略其影响。

图8 胶结层弹性模量与泊松比对平均应变传递率影响
3.2 涂布层对平均应变传递率的影响分析
涂布层作为结构最外层,对应变传递率的影响至关重要。提高涂布层和胶结层的平均应变传递率,有利于提高结构传感精度。表3胶结层的结构相关参数取值情况。

表3 涂布层结构参数
3.2.1 涂布层厚度对平均应变传递率影响
当涂布层弹性模量Em=3.59 GPa时,分析了基涂布层厚度对平均应变传递率的影响效果。从图9可以看出,随着涂布层厚度由0 mm增加至10 mm时,平均应变传递率增大,变化趋势近似直线上升。因此,为保证较高的应变传递率,应适当增加涂布层厚度。

图9 涂布层厚度对平均应变传递率的影响
3.2.2 涂布层弹性模量与泊松比对平均应变传递率影响
图10为涂布层弹性模量和泊松比对平均应变传递率的影响,图中涂布层弹性模量Em在2~10 GPa波动,泊松比在0.3~0.5波动。数据表明,随着涂布层弹性模量增大,平均应变传递率曲线下降。因此,涂布层选取较低弹性模量与硬度较大的材料可以起到保护光纤与提高结构的应变传递率的作用。

图10 涂布层弹性模量与泊松比对平均应变传递率影响
3.3 误差来源分析
通过建立应变传递率数学模型,结合Anays有限元仿真结果分析可得,结构中间区域应变传递率为1,两端逐渐减小。在实验与应用中,选用弹性模量为4 GPa,泊松比为0.38的胶粘剂粘接1 mm;涂布层选用弹性模量为2 GPa,泊松比为0.3,厚度半径为10 mm的材料,可有效提高应变传递率。
在实际应用中应考虑到以下几点问题导致误差:
1)由于理论计算时将光纤的纤芯与包层统一当作玻璃纤维材料,采用玻璃的材料参数进行理论计算,得到的结果会存在一些偏差;同时,在实际问题中考虑到材料结构并不均匀,会对测量过程产生较大影响。
2)由于在现实中难以匹配到与理论计算出的最优结构参数一致的材料,因此,在实际应用过程中只能选用参数相近的材料,而这将会在实验与应用过程中与理论值产生一定的偏差。
3)用于检测瑞利背向散射光的过程存在误差[14],由于在采用OFDR测量时,被测光纤与参考光纤存在光路差,反射光干扰本地光,产生位置依赖信号。当轴向应变或温度发生变化时,由于弹性光效应和热光效应,光程随长度和折射率的变化而变化,将会导致光谱位错。在不同空间分辨率下,OFDR光谱位错约为25 %(2 mm),50 %(1 mm)和62.5 %(0.8 mm)。
4)在被测物体发生形变过程中,结构各层、结构与被测物体之间也会产生相对滑移,在实际检测过程中会对测量结果产生一定的影响。
4 结束语
通过分析光纤分布式形状传感器传感层与涂布层微观应变传递率理论模型表明:所构建的理论模型与有限元仿真结果变化趋势一致。通过分析模型中各个参量变化对传递率的影响,发现结构平均应变传递率随涂布层厚度增加而增大,随胶结层厚度增大而减小。涂布层与胶结层材料弹性模量与泊松比同样对结构应变传递率有很大的影响。结构平均应变传递率随涂布层泊松比与弹性模量减小而提高,胶结层弹性模量增大,泊松比减小同样会提高结构的平均应变传递率。因此,在工程应用中,通过适量调整材料结构参数,从而提高应变传递率,可较为精确地得到被测物体的形变值。

