基于主成分回归的土壤有机质高光谱特性分析

曾远文

(重庆市地理信息和遥感应用中心, 重庆 401147)

0 引言

土壤有机质(soil organic matter,SOM)作为作物生长的重要养分来源,其含量的多少对作物的生长发育有着显著的影响[1]。因此，如何准确快速地获取土壤有机质含量,科学指导农业现代化管理,已成为相关专家学者积极探索的热点问题。光谱分析技术的飞速发展,为上述问题的研究提供了新的路径,由于其具有的快速、便捷、无污染的特点,已在农业及其他领域得到了广泛的应用[2-6]。实验和研究表明,土壤有机质作为影响土壤光谱特性的重要因素之一,其在可见光和近红外区域有独特的光谱特性[7]。土壤光谱反射率与有机质含量呈显著负相关,有机质含量可以从土壤反射光谱中得到一定程度的反映[8-9]。

为进一步研究土壤有机质的高光谱反射特性,以及土壤样本的不同粒径水平和不同光谱变换形式对土壤有机质反演模型的影响程度,本研究通过相关分析和主成分回归分析探讨了不同粒径水平下和不同光谱数学变换形式下的土壤有机质的光谱特性,并浅析了实验室土壤样本制备的最优粒径大小及光谱变换形式,以期为后续研究提供一定的参考和借鉴。

1 材料

1.1 土壤样本的制作与处理

将野外采集的37个土壤样本自然风干,并研磨成1 mm、0.5 mm、0.25 mm、0.125 mm、0.075 mm这5个不同等级的粒径。由于在试验中使用了样本粉碎机,导致有的样本中1 mm和0.5 mm粒径的样本数量较少,结果0.075 mm、0.125 mm、0.25 mm粒径的样本数都为37个,0.5 mm的有24个,1 mm粒径的样本量为22个。土壤有机质含量采用重铬酸钾氧化—外加热法测定,主要原理和操作步骤详见《土壤农化分析》[10]。各粒径水平下有机质统计结果如表1所示。

表1 不同粒径样本有机质含量统计表

1.2 室内光谱测量与处理

1.2.1光谱测定

用ASD FieldSpec 3光谱仪进行室内光谱测量,测量时将装有样品的石英玻璃皿放置在黑色天鹅绒中心,并使用功率为50 W的卤素灯和8°视场角的探头,探头垂直于土样表面,到土样表面距离15 cm,光源入射方向与垂直方向夹角15°,光源到土样中心的距离为30 cm,各几何参数在实验过程中保持不变。把适量经过处理的土壤样品放入盛样皿中,用玻璃压实,使其表面尽量平整,为了消除土样反射光谱各向异性的干扰,测量时转动盛样皿三次,测量土样的4个方向的光谱曲线(每个方向取5条,一共20条光谱曲线),将各方向的光谱曲线算术平均后得到该土样的反射光谱数据。

1.2.2光谱数据预处理

对获取的光谱曲线进行断点校正、10 nm间隔重采样、低信噪比波段及水吸收峰剔除,具体的剔除范围为：350～395 nm、1 345～1 515 nm、1 795～2 025 nm、2 405～2 500 nm,经过以上预处理之后最终剩下158个波段。

1.2.3光谱曲线数学变换

本研究除了直接用原始光谱反射率进行分析外,参照前人的研究还对土壤光谱曲线进行数学变换,包括反射率求对数lgR、反射率倒数1/R、反射率倒数的对数lg (1/R)、反射率对数的倒数1/lgR、反射率求一阶微分R′、反射率倒数求一阶微分(1/R)′、反射率对数的一阶微分(lgR)′、反射率倒数的对数的一阶微分(lg (1/R))′、反射率对数的倒数的一阶微分(1/lgR)′、反射率求二阶微分R″、反射率倒数求二阶微分(1/R)″、反射率对数的二阶微分(lgR)″、反射率倒数的对数的二阶微分(lg (1/R))″、反射率对数的倒数的二阶微分(1/lgR)″、吸收深度(Depth)提取等。

2 研究方法

2.1 主成分回归

在进行主成分分析时按以下步骤进行：

(1)对反射光谱进行预处理和相应的数学变形;

(2)土壤有机质含量和反射率及其数学变形进行单相关分析,筛选出相关性达到显著的波段(P<0.01);

(3)用这些被筛选出来的波段进行主成分回归分析。

这样保证了在进行主成分分析时不丢失与土壤有机质相关性显著的波段,又相当于进行了数据降维,增加了数据处理的效率。

2.2 模型质量评价参数

回归模型的精度和预测能力通过以下参数进行评价：

(1)决定系数R2。包括建模决定系数、交叉检验绝对系数和预测绝对系数。

(2)均方根误差。包括建模均方根误差Rc、交叉检验均方根误差Rcv和预测均方根误差Rp。计算公式如下所示：

(1)

(2)

(3)

式中,Ym和Yp分别表示实测值和预测值;Nc、Ncv、Np分别表示建模、交叉检验和预测样本数。

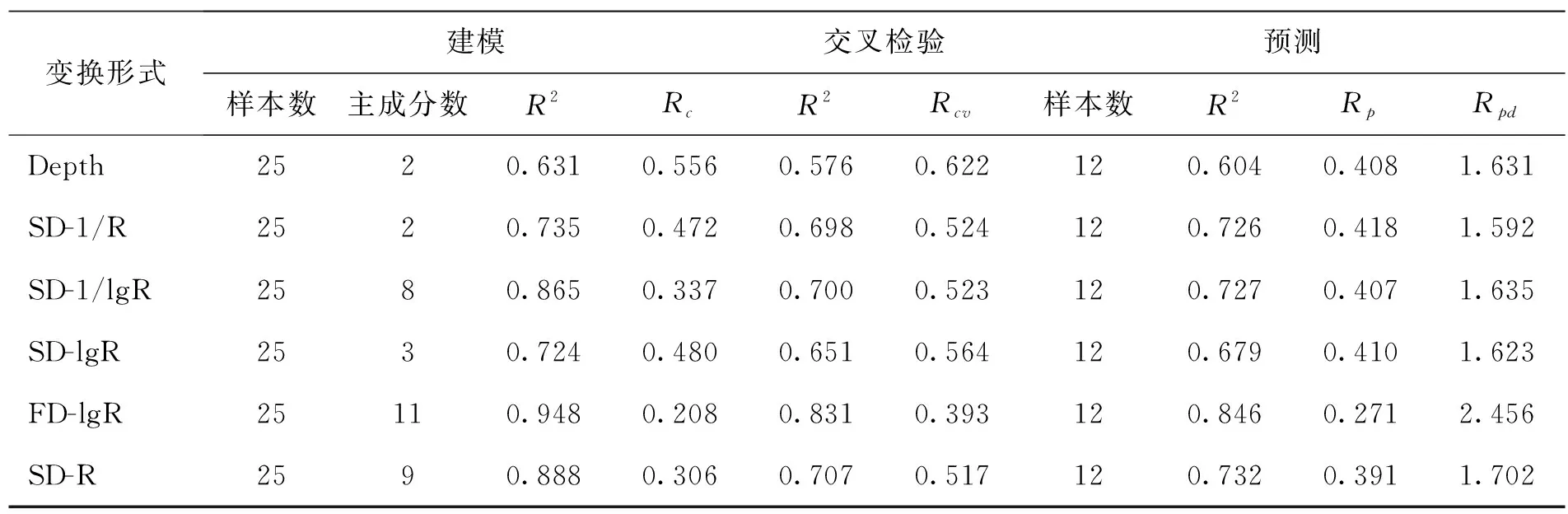
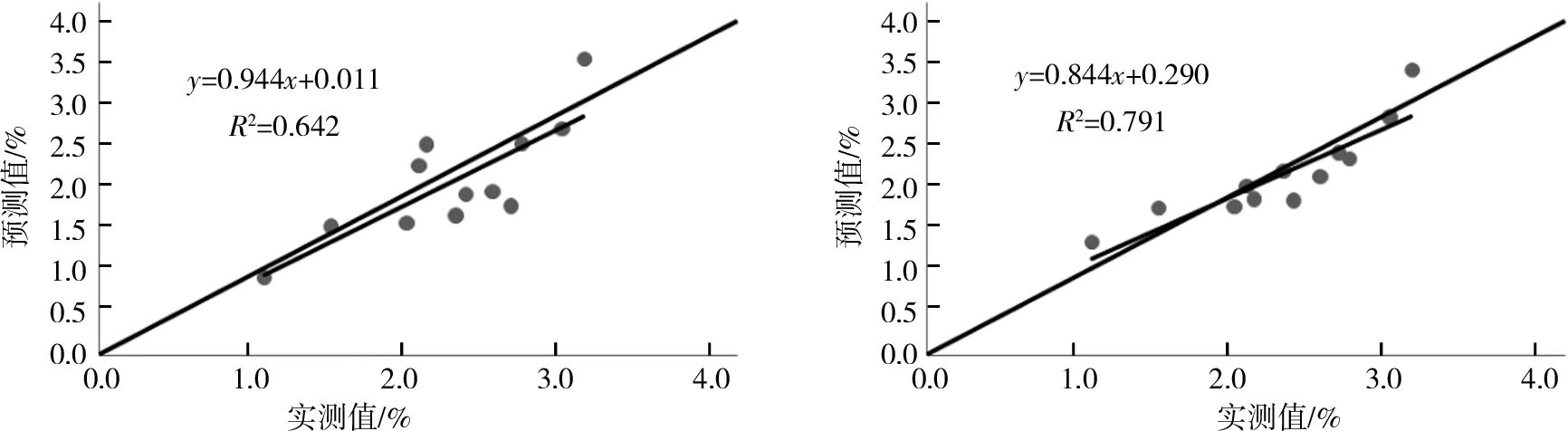
(3)预测相对偏差Rpd。当Rpd>2时,回归模型具有极好的预测能力;当1.4

模型的决定系数R2和预测相对偏差Rpd越大,均方根误差Rc、Rcv、Rp越小,说明模型的精度越高。

3 结果与分析

3.1 相关性分析

将有机质含量和土壤光谱反射率及其变化形式在各个不同的粒径水平下进行相关性分析。结果显示，有的变换形式在有的粒径水平上全波段范围内与有机质的相关性均未达到显著水平(P<0.01),其中只有吸收深度(Depth)、反射率对数的一阶微分(FD-lgR)、反射率对数的二阶微分(SD-lgR)、反射率的二阶微分(SD-R)、反射率倒数的二阶微分(SD-1/R)和反射率对数的倒数的二阶微分(SD-1/lgR)这6种变换在5个粒径水平上均有与有机质含量显著相关的波段存在。

比较这6种变换形式各个粒径水平下与有机质含量的相关性,如表2所示,结果显示，达到显著相关性的波段大都集中在UV ～VNIR波段范围内,且最大相关波段主要分布在475～600 nm波段范围内(对数的一阶微分除外),这与前人的研究结论相似;达到显著相关性的波段数无论在哪个粒径水平下都是对数的一阶微分这种变换形式最多,倒数的二阶微分最少,且相关系数的均值在各个粒径水平下也是前者大于后者,说明就这两种变形而言对数的一阶微分比倒数的二阶微分更为有效;各个粒径水平下相关系数均值最大的都是对数的二阶微分。

表2 反射率各种变换形式与有机质含量相关分析结果

3.2 主成分回归分析

筛选出的波段相互之间存在多重共线性,直接进行回归分析将不能解决数据冗余问题,而且还难以得到精确的模型,因此用筛选出来的波段进行主成分分析,消除自变量间的自相关性。数据集分为建模集和预测集,在0.075 mm、0.125 mm、0.25 mm三个粒径水平下按随机的原则选取建模集样本25个,预测集12个,0.5 mm粒径水平为16个和8个,1 mm粒径水平为15个和7个。

主成分分析之前需要对数据进行标准化处理,建模过程中选用“Full Cross validation”的方法来确定模型需包含的潜变量的个数和防止过度拟合,分析结果如表3～表7所示。

表3 0.075 mm粒径水平下的回归分析结果

表4 0.125 mm粒径水平下的回归分析结果

表5 0.25 mm粒径水平下的回归分析结果

表6 0.5 mm粒径水平下的回归分析结果

表7 1 mm粒径水平下的回归分析结果

从主成分回归分析结果可以看出,同一个粒径水平下不同的变换形式所建立的模型精度有很大的差异性,同理，一种数学变换形式在不同的粒径水平下所建立的模型精度也不一样,说明光谱数据的处理方法和土壤样本的粒径大小共同影响着回归模型的结果。

在0.075 mm粒径水平下，以反射率的对数的一阶微分这种变换形式建立的模型预测精度最高,决定系数为0.848,预测均方根误差最小为0.230。其次是对数的倒数的二阶微分这种变换形式的模型预测的决定系数为0.788,均方根误差为0.267；在0.125 mm水平下，预测精度最高的也是对数的一阶微分,决定系数为0.846,均方根误差为0.271,反射率二阶微分、反射率对数的倒数二阶微分、反射率倒数二阶微分三种形式预测精度相当；0.25 mm水平下预测精度最高的依然是对数的一阶微分这种变换形式,其次是对数的二阶微分和Depth；0.5 mm水平下最好的倒数的二阶微分其决定系数为0.831,紧随其后的是对数的二阶微分为0.818；1 mm水平下最优模型为对数的二阶微分建立的,决定系数达到了0.922，远高于其他变形,最差的为反射率的二阶微分,决定系数仅为0.383。

观察各个结果的Rpd可以发现，0.075 mm水平下均大于了1.4,说明均可对有机质做出粗略的估计,其中最大的为反射率对数的一阶微分达到了2.518,能准确地估算土壤有机质含量。0.125 mm水平各个变形的Rpd也都大于了1.4,最大的也是反射率对数的一阶微分为2.456。0.25 mm水平下反射率对数的倒数的二阶微分为1.399，与1.4非常接近,其他的都大于1.4,最大值还是对数的一阶微分为2.797,且总体上说这组值都比其他水平的要大。0.5 mm水平下有一半的变形未达到1.4,但都很接近1.4,最大值是对数的二阶微分为1.973。1mm水平也有一半未达到1.4,最大的是对数的二阶微分为2.938。

在各个粒径水平上分别求取预测决定系数和均方根误差的平均值,其中决定系数最大的是0.25 mm水平，为0.750。其次是0.075 mm水平，为0.724。呈现出0.25 mm> 0.075 mm>0.125 mm>0.5 mm>1 mm的规律,均方根误差最小的是0.25 mm水平,排序为0.25 mm<0.075 mm<0.5 mm<1 mm<0.125 mm。所以，从模型的预测精度考虑，0.25 mm水平总体优于其他粒径水平,当粒径从0.25 mm减小到0.125 mm时决定系数有所降低,但是在继续减小到0.075时决定系数却开始增大,但是未达到0.25 mm水平的值,说明土壤样本并不是越细越好,而是存在一个度。当粒径从0.25 mm增大到0.5 mm时模型决定系数迅速减小，伴随着的是均方根误差的增大,继续增大粒径时这种规律依然存在,所以可以粗略地认为当粒径大于0.25～0.5 mm这个范围之后,模型的精度随着粒径的增大而减小,但是这个结论可能会受到样本容量的影响。0.075 mm、0.125 mm、0.25 mm水平的样本数都是37个,但是0.5 mm是24个,1 mm是22个,所以决定系数的大小是否还受到样本容量大小的影响还有待进一步验证,比较前3个粒径水平可以发现,0.25 mm水平明显优于其他两个水平,比较0.5 mm和1 mm发现前者优于后者,所以可以断定回归模型建立的最优粒径水平存在于0.125 mm～0.5 mm之间,但具体是哪个值本文未做深究,这为今后实验室样本的制备提供了一定的参考。

同理,分析各个变换形式的决定系数和均方根误差,决定系数排序为SD-lgR> FD-lgR> SD-1/R>Depth> SD-1/lgR>SD-R,均方根误差排序为FD-lgR

为了研究粒径大小和反射率变换形式两者对模型精度的作用大小,同时又排除样本容量大小的影响,因此摒弃1 mm和0.5 mm这两个粒径水平之后,分别求不同变换形式和粒径水平下建立的回归模型的决定系数的变异系数。其中，不同粒径水平决定系数的变异系数为2.28%,同理可得不同变换形式的为8.37%。可知两者决定系数的变异系数相差很大,说明数学变换对回归模型预测精度的影响要大于粒径水平,所以在实验室对土壤样本进行预处理固然重要,但是对光谱数据的数学变形同样不可忽视。

3.3 模型精度和预测能力分析

图1展示的是在0.25 mm粒径水平下各个变换形式主成分回归模型预测值与实测值的散点图。可以看出，除了反射率的二阶微分和吸收深度之外,其他变换形式的样点多半分布在1∶1直线下端,说明预测值普遍比实测值偏小,反射率的二阶微分样点虽然均匀分布在1∶1直线两端但是平均距离较大。综合来说，反射率对数的一阶微分建立的模型最优,且当有机质含量在2.0%～2.5%时预测结果不佳,样点距离1∶1直线明显远于其他值。

(a)对数的一阶 (b)吸收深度

(c)对数的倒数的二阶 (d)对数的二阶

(e)反射率的二阶 (f)倒数的二阶

4 结束语

利用主成分分析的方法实现了土壤有机质反演模型的建立,在分析前首先通过相关性分析筛选出与有机质含量有显著相关性的波段,实现了数据的降维但又不丢失土壤有机质的敏感波段,然后用筛选出来的敏感波段来进行主成分分析,消除自变量之间的多重共线性,最后用求出的主成分与有机质含量进行多元线性回归分析,建立了反射率的各种数学变形在各个粒径水平下的回归模型。

分析粒径大小对模型精度的影响发现,土壤样本并不是研磨得越细越好,也不是越粗越好而是存在一个度。实验中建立回归模型的最优粒径水平存在于0.125 mm～0.5 mm之间,分析不同变换形式对模型预测精度的影响可知，建模之前对光谱数据进行预处理是相当有必要的,特别是进行对数变化之后再求微分。研究还发现，不同变换形式对模型精度的影响要大于不同的粒径水平,这将为今后相关研究提供一定的参考。