对线性调频步进频雷达相参干扰方法研究

郭慧峰，鲁永为，山世浩，徐亚波

（光电对抗测试评估技术重点实验室，河南 洛阳 471003）

0 引言

线性调频步进频雷达通过发射一组载频线性跳变的脉内线性调频脉冲串，兼具线性调频信号和步进频率信号的优点，在不增加系统瞬时带宽的情况下用数字信号处理的方法合成高分辨距离像，同时采用宽脉冲发射保证了足够大的作用距离。由于步进频雷达利用回波信号的延时相位通过IFFT 处理得到高分辨率位置信息，而传统的噪声干扰信号不相参，干扰效果不明显，因此线性调频步进频雷达具备较强的抗干扰能力，在精确制导武器中得到了广泛的应用。

文献[1]分析了噪声干扰对单脉冲频率步进雷达的影响，并分析了基于DRFM 的频率步进频雷达欺骗干扰；文献[2]分析了移频干扰对脉冲压缩雷达的影响；文献[3]提出采用多假目标欺骗和随机脉冲卷积调制干扰对步进频雷达实施干扰，但没有考虑由采样时长带来的干扰信号相对真实目标回波的延时，使得假目标无法进入检测波门，也就无法对真实目标进行有效干扰，随机脉冲卷积调制干扰扩大了假目标分布范围，但也降低了干扰信号的处理得益，降低了干扰效果。

1 线性调频步进频信号处理

线性调频步进频雷达信号是把步进频信号中的常载频子脉冲换成线性调频子脉冲，每个子脉冲都是线性调频信号，子脉冲的中心频率均匀步进，如图1所示。

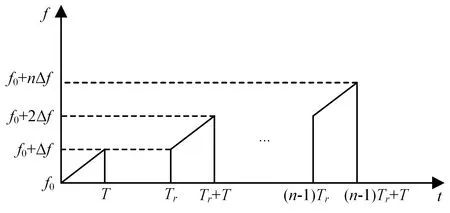
图1 线性调频步进频信号频率变化规律

线性调频步进频雷达接收到回波信号后首先对子脉冲进行脉冲压缩，然后再进行脉冲串间的相参合成，如图2 所示。这样既保留了子脉冲信号低采样率和窄带处理的优点，又具备线性调频信号大时宽带宽积的特点，集目标探测跟踪和输出高分辨一维距离像2 种功能于一体，极大提高了对目标的精确识别和跟踪能力。

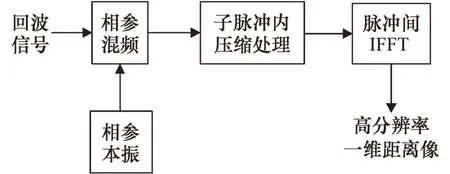
图2 线性调频步进频信号处理流程

设线性调频步进频信号回波表达式为：

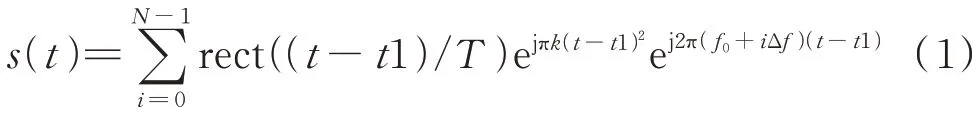
式中，1=iT+，T为脉冲重复周期，Δ为频率步进大小，=/为子脉冲调频斜率，为调频信号带宽，一般不大于Δ，为信号脉宽，为调频子脉冲个数，为雷达起始频率,为目标回波的时间延时。

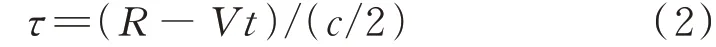
式中，为目标距离，为目标速度，本文假设=0，为光速。

()与接收机参考信号混频后的输出为：

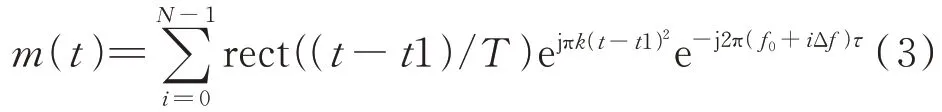
根据脉冲压缩原理，()经过匹配滤波器后输出为：

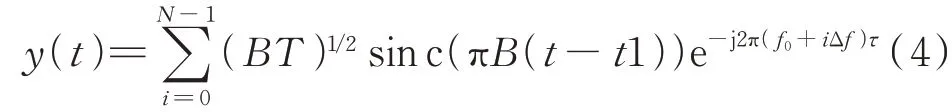
取采样时刻为=iT+2/，可以得到慢时间维脉压输出采样为：

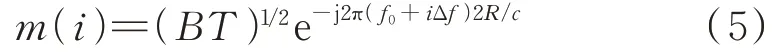
由式（5）可以看出脉压后子脉冲在慢时间维进行了e相位调制，对其进行IFFT 处理后的结果为：

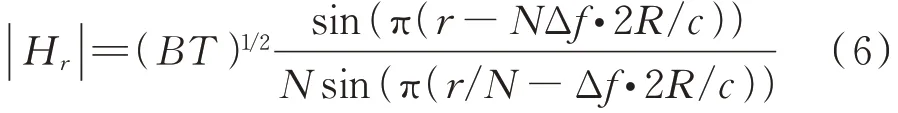
式（6）为离散sin c 函数，距离分辨力为c/(2Δ)，相对单个子脉冲至少提高倍。

2 间歇采样干扰模型

间歇采样干扰是一种基于DRFM 的收发分时干扰样式，通过利用雷达对回波信号的匹配处理，可以产生假目标干扰效果。基本的间歇采样干扰样式为单次转发干扰方式，如图3 所示。

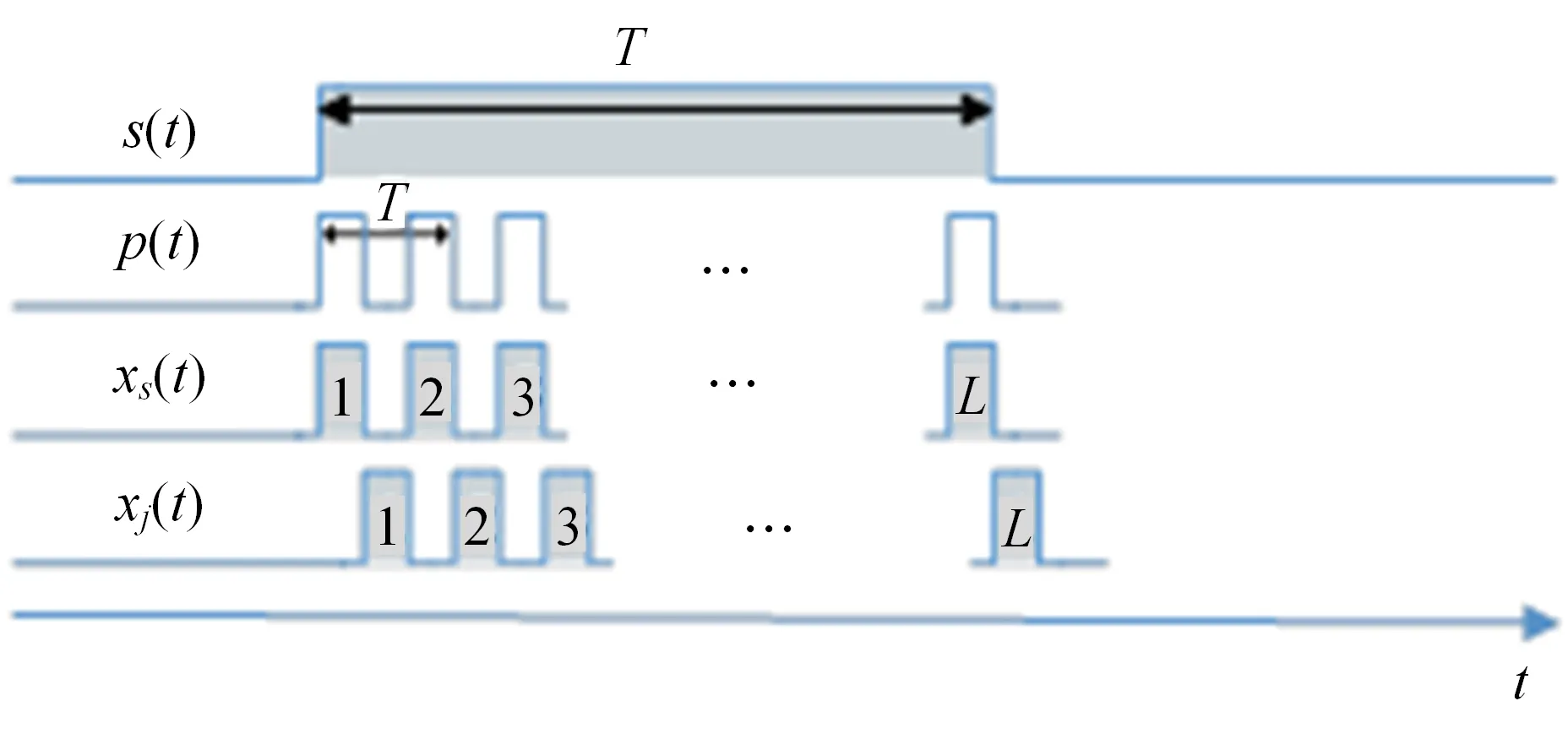
图3 间歇采样单次转发干扰时序

其干扰时序为：

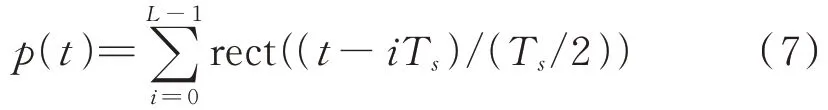
式中，间歇采样周期为T，对于单次转发干扰方式，其单次采样时长和单次干扰时长均为T/2。

()频谱表达式为：

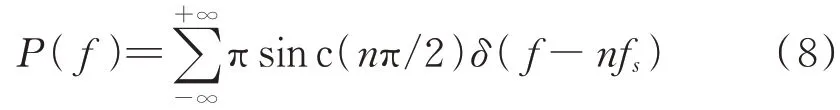
设对线性调频步进频信号间歇采样后的信号为x()，则x()=()()，干扰信号x()为对采样信号x()进行T/2 的延时，结合频率搬移对脉冲压缩的影响可得到x()对应脉压输出为：

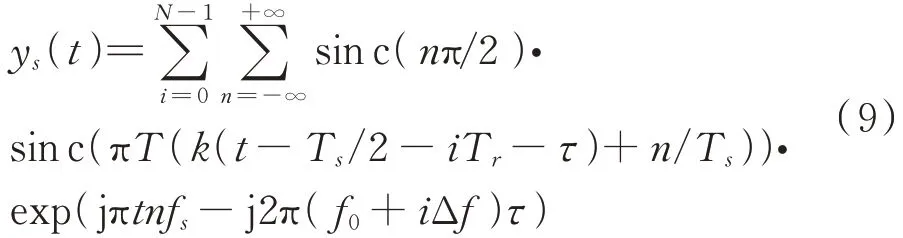
可以看出，对于每个调频子脉冲的脉压结果，当=T/2+iT+-nf/时刻出现峰值，且=0，=iT+幅度最大，称为主假目标。

设真实目标位置=19.7 km，脉宽=80 μs，带宽=5 MHz，T=4 μs，间歇采样干扰信号脉压结果如图4 所示，形成主假目标位于距离20 km 处，滞后于目标0.3 km，幅度明显高于其它假目标。

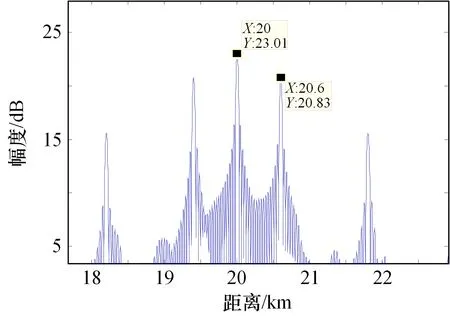
图4 间歇采样信号脉压结果

3 间歇采样延时叠加移频干扰

步进频雷达通过多脉冲相参合成实现高距离分辨力，假设频率步进大小Δ=16 MHz，子脉冲个数=16，则距离分辨力/(2Δ) 为0.59 m。基 于DRFM 体制的间歇采样干扰受硬件资源限制，目前采样时长最小约0.5 μs，采用常规的间歇采样干扰产生的假目标至少滞后于真实目标75 m 左右，超出目标检测波门范围，不能达到干扰目的。

本文提出在间歇采样单次转发干扰的基础上，一方面对转发样本进行频率调制，使得干扰信号经脉压处理后形成的假目标前移至真目标检测参考单元内，获得对真目标干扰的效果；另一方面对转发样本进行基于FPGA 时钟周期的纳秒级延时叠加，形成覆盖一定距离范围间距为米级的多扰时序，如图5 所示，其中Δ为转发样本延时大小，f为移频大小，为延时叠加个数。

图5 间歇采样延时叠加移频干扰时序

干扰信号表达式为：

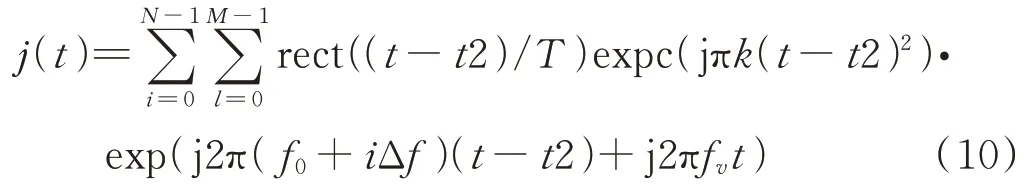
式中，2=T/2+iT+()+Δ。

()与接收机参考信号混频后的输出为：

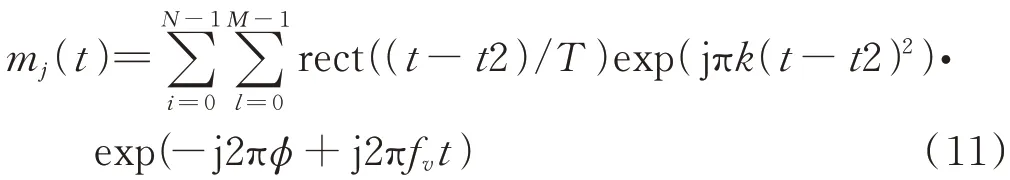
式中，=(+Δ)(()+T/2+Δ)。

m()经过匹配滤波器后输出为：

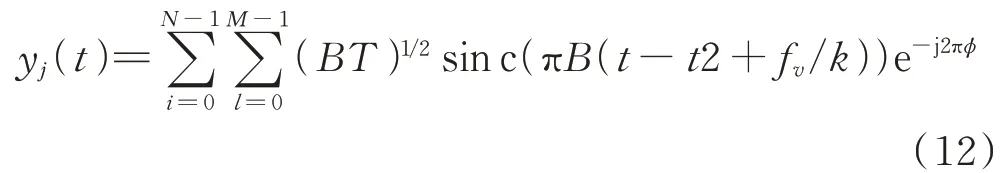
由式（12）可以看出，对于每个子脉冲干扰信号，脉压后生成了个假目标，但由于假目标间距小，无法从距离上分辨，假设真目标和所有假目标位于真目标附近同一个距离单元/(2)内，取采样时刻为=2-f/，由式（11）可以得到采样数字信号为：

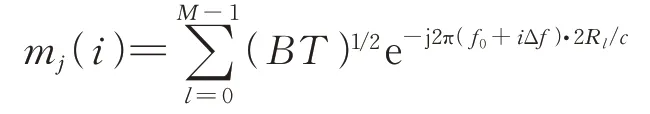
式中，R=+(T/2+Δ)/2。

对其进行IDFT 处理后的结果为：

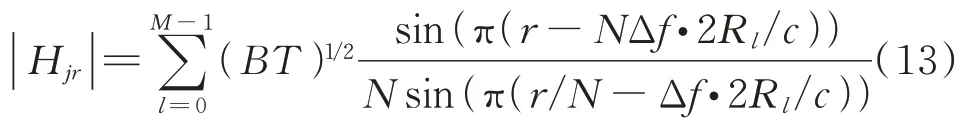
式（13）距离分辨力为/(2Δ)，其包络为个离散sin c 函数的叠加。结合式（11）可以看出，采用间歇采样延时叠加移频干扰，可以形成个间距为Δ/2的假目标，假目标与真实目标距离为(T/2+Δtf/)/2，结合雷达信号调频斜率合理设计间歇采样周期T及移频大小f，可以使假目标密集分布于真实目标周围，获得对步进频雷达相参压制干扰的效果。

4 仿真实验

设步进频雷达信号脉宽=16 μs，带宽=16 MHz，频率步进大小Δ=16 MHz，子脉冲个数=16，干扰机采样时长0.5 μs，延时叠加个数为10，目标位于656.2 m 处，对雷达信号和干扰信号进行脉冲压缩仿真处理。

取Δ=1 μs，f=0 时，仿真结果如图6 所示。

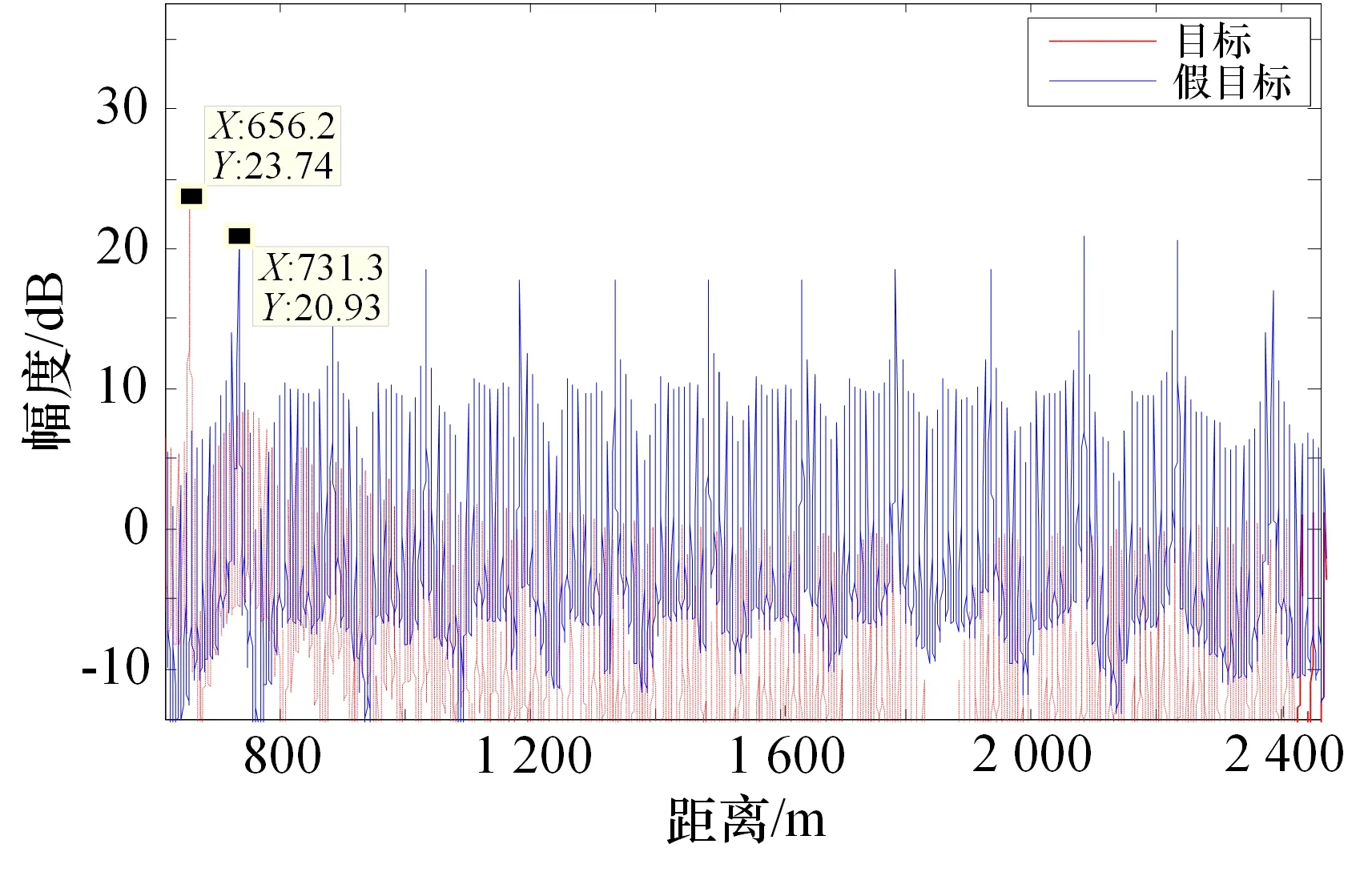
图6 Δt=1 μs 时延时叠加干扰仿真结果

由图6 可以看出，经脉压后相邻假目标间隔约150 m，且第一个假目标滞后于真实目标约75 m，与干扰机采样时长0.5 μs 相对应。此时假目标距离真实目标过远，且分布过于分散，达不到压制干扰目的。

图6 定位误差的分布图（12 h）

取Δ=10 ns，f=0 时，仿真结果如图7 所示，假目标集中分布，但第一个假目标滞后真实目标约75 m，仍达不到压制干扰目的。

图7 定位误差的分布图（24 h）

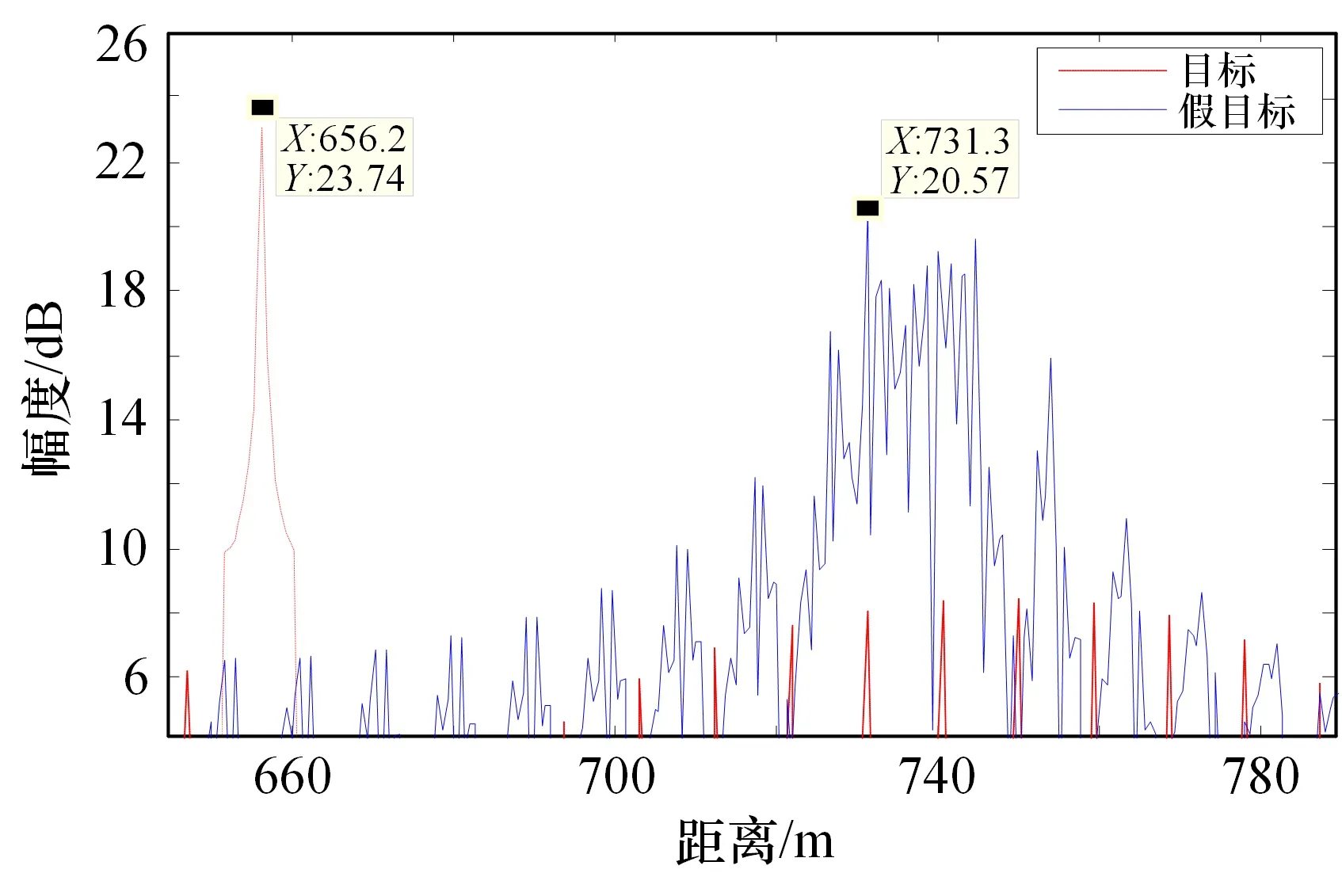
图7 Δt=10 ns 时延时叠加干扰仿真结果

取Δ=10 ns，f=0.55 MHz 时，仿真结果如图8所示，假目标密集分布于真实目标前后约10 m 内，在雷达检测单元内形成压制干扰态势。

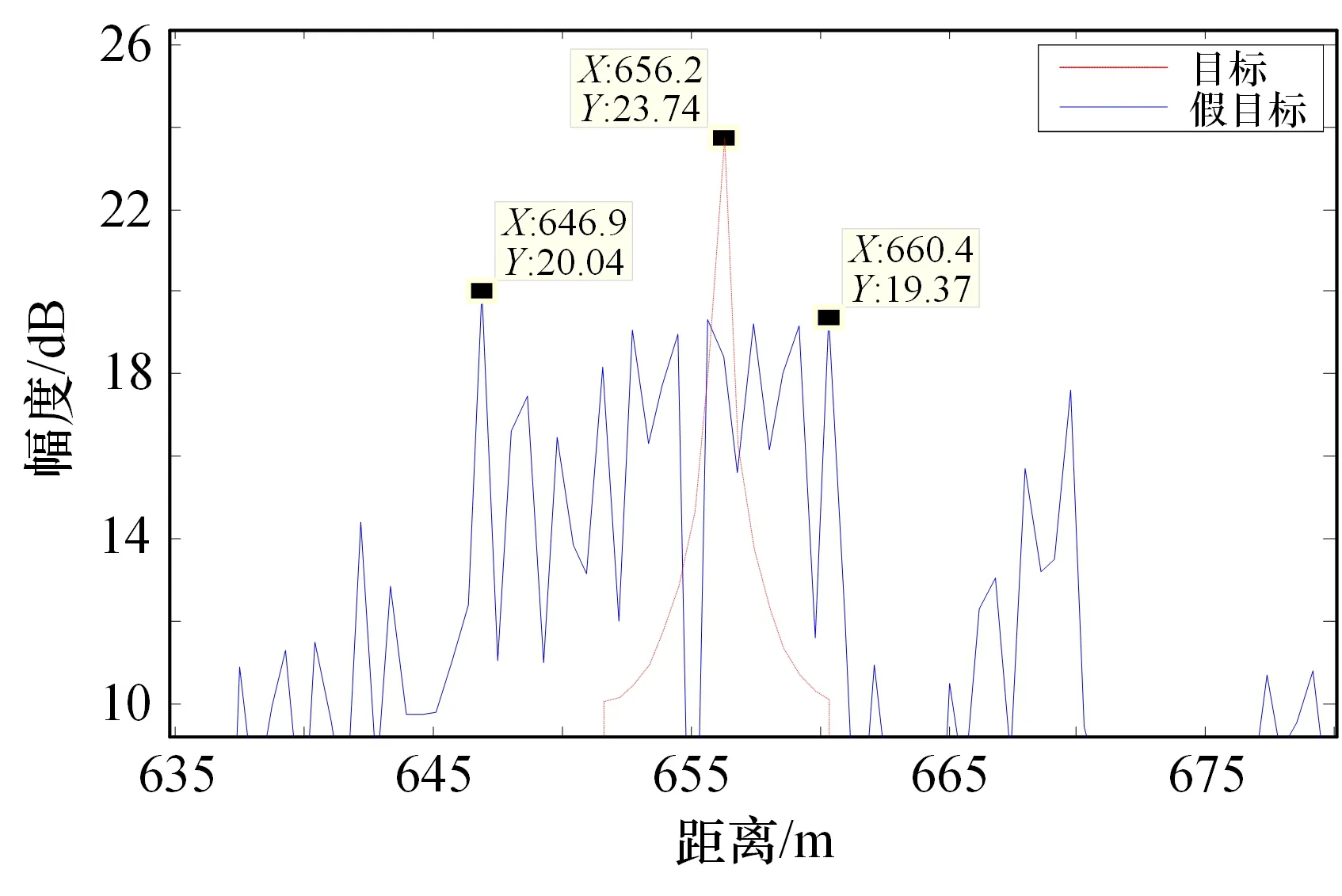
图8 纳秒级延时叠加+移频干扰仿真结果

5 结束语

本文针对线性调频步进频雷达的信号处理特点，在延时叠加间歇采样干扰的基础上，提出了一种基于FPGA 时钟周期的纳秒级叠加+频率调制的干扰时序设计，形成对真实目标的密集压制干扰。通过对干扰信号处理过程进行理论推导，并结合仿真实验，验证了该干扰设计的可行性。■