基于队形控制的电子对抗智能体协同方法

姜福涛，黄学军

（1.中国人民解放军92768 部队，广东 汕头，515800；2.国防科技大学电子对抗学院，安徽 合肥，230037）

0 引言

第二次纳卡冲突让世人领略了无人作战的威力，电子对抗无人装备（简称无人装备，下同）运用问题成为关注热点。对海军濒海要地防御来说，适当增加无人装备可以提高作战效费比，而且电子对抗无人装备集群（简称集群，下同）已经成为研究无人作战的新课题。但受某些特定地域地理环境、电磁环境影响以及部署要求，集群需保持一定的队形，并通过优化队形充分获取战场态势、利用火力和电磁盲区规避海上高威胁区。队形控制是集群协同的基础性问题，根据相关文献提出“领导跟随”和“邻接跟随”2 种协同队形控制模式，并根据C++仿真结果，提出集群协同的相关建议。

1 “领导跟随”模式下集群协同控制方法

在未来局部战争中，战场上的电子对抗无人装备可能来自不同军种，发射点随机性较大，组织协同时需要对其位置进行初始化处理。参照当前演训任务中对作战模块的编号方法，也可对无人装备进行编号。

1.1 “领导跟随”模式下无人装备编号序列生成方法

“领导跟随”模式运用在作战层面，关键是确定领航无人机。根据“领导跟随”算法，一般取集群的几何中心作为中心点，把距离中心最远的点定为领航无人机，把与的连线作为初始运动方向，最后构建一个坐标系（→→），为所有无人装备分配序号，并按升序排列轴坐标值。在轴方向，如果坐标值为负则编号为奇数，若为正则编号为偶数，按照此规律轮流编号，直到无人装备都被编号。在另一个半平面内的成员紧随先编号的半平面的最后一个成员连续编号，如图1 所示。通过计算机仿真演示了无人装备的序列分配结果，如图2 所示。

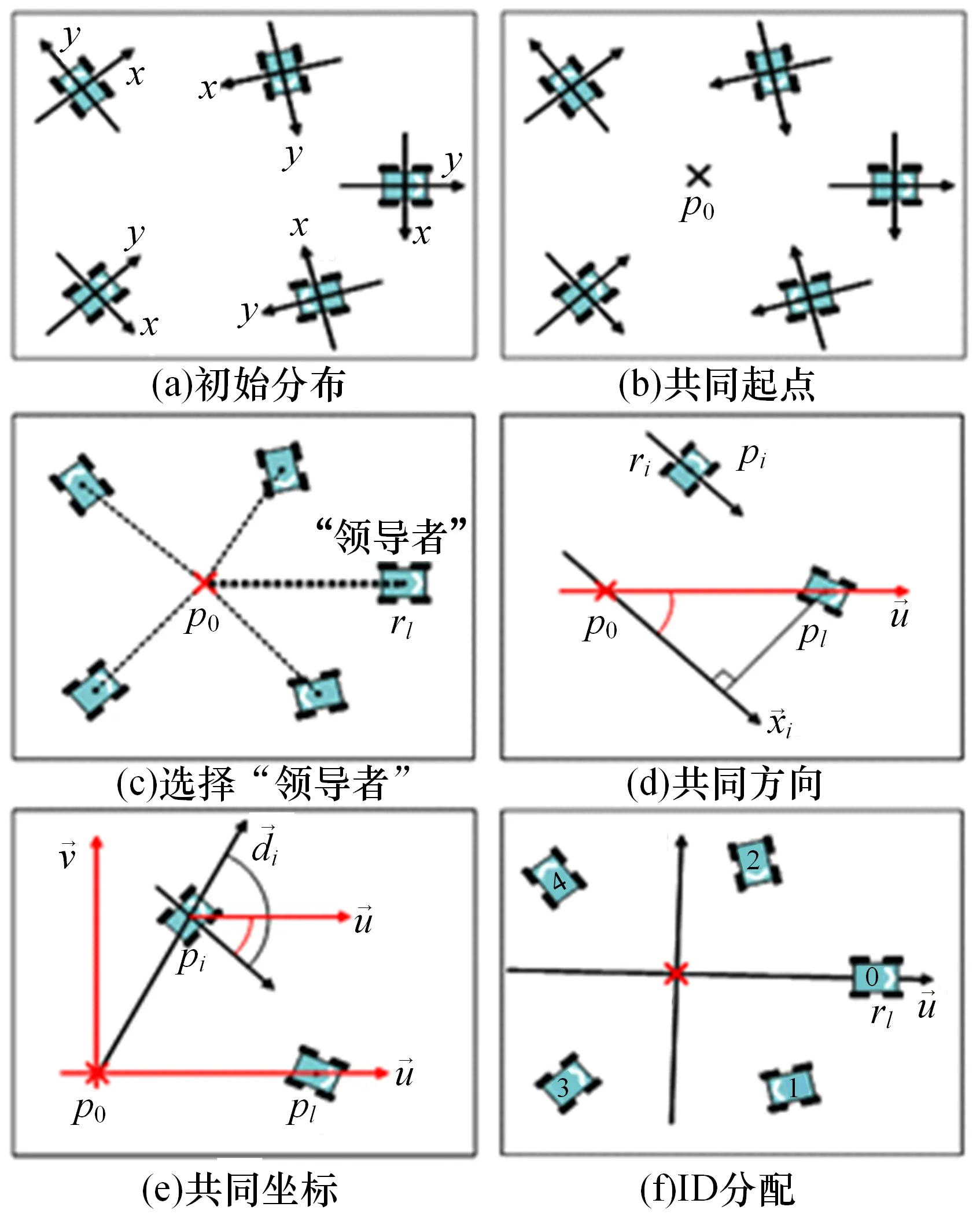
图1 集群序列实现示意图

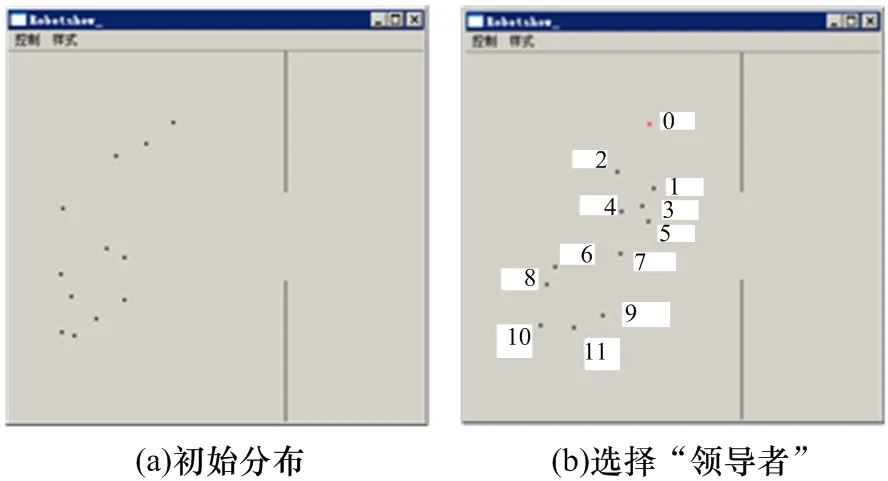
图2 无人装备序列分配仿真结果

1.2 “领导跟随”模式下无人装备协同算法

一般情况下，无人装备进行集群机动时，要考虑在三维空间的编组，为简化问题，本文暂时以平面研究为主，主要分析单线和多线队形。单线队形包括水平线、垂直线、弧形、圆、楔形等，重点要考虑无人装备之间的距离和角度。其算法为：

Step1：输入序列号，的坐标和队形结构。

Step2：判断序列号奇偶性，若为偶数，标记为1，反之为-1。

Step3：计算目标位置坐标。

Step4：输出目标坐标值。

多线队形还要考虑水平线的数目，判断队形是水平型还是垂直型，具体算法如下：

Step1：输入序列号，的坐标和协同队形结构。

Step2：计算水平线数，假设无人装备数目为,如果是多线纵队（列数为），且%=0，等于[]，反之，：=[/]+1；如果是多线横队，:=。

Step3：计算队形长度。如果/2 的余数是0，：=[((ID%)+1)/2]×d；如果余数不为零，则需进一步判定

①当ID/的商是偶数时，：=[((ID%)+1)/2]×d，

②若为奇数且序列号为偶数时，：=[((ID%)+2)/2]×d，

③若为奇数且序列号为奇数时：=[(ID%)/2]×d。此处ID为第个无人 装备的序列号。

Step4：进行标记，同单线队形标记。

Step5：计算第个无人装备目标位置坐标，u:=u-[ID/]×d,v:=×。此处，代表Step4 中的标记值。

Step6：输出目标坐标值。

确定无人装备在集群中的目标位置后，下一个重要问题就是正确设置移动路径，以节省队形形成时间、缩短形成路程。由于电子对抗力量时效性要求高，经常需要紧急编队，所以缩短编队时间、赢得时间优势很重要。但在设置路径时，还需要解决避碰问题，为此提出以下算法：根据初始位置和在目标位置建立模型，计算任意2 点之间是否有碰撞点。假设无人装备速度一致，在每个运动周期内距离记为一个步长，当2 个起始位置和路径形成等腰三角形，则会出现碰撞点，记为，此时序列号小的先通过。

依上述算法仿真得到图3-4 所示结果。图3 仿真了12 个无人装备如何形成圆形队形；图4 通过改变角度值，形成不同队形；图5 演示不同数量的无人装备形成扇形。

图3 领导跟随法中圆形队形生成仿真

图4 12 个无人装备形成5 种队形的仿真结果

图5 不同数目的无人装备形成的扇形

1.3 无人装备协同运动与队形转换

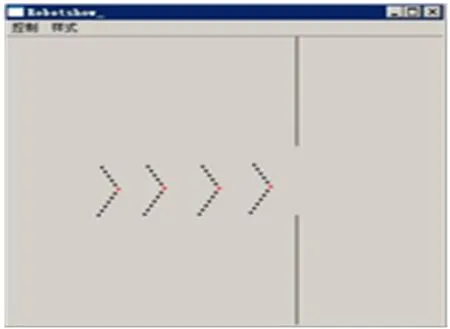
图6 楔形队伍协同运动仿真（任务完成需要5.74 s）

队形转换算法的核心思想是确定最短距离和最小时间。传统算法会采用两点位移法，计算新旧坐标位移向量，但会存在延迟。为此进行适当优化，建立一个包含不同队形参数和队形转换参数数据库，在转换队形时可直接调用子函数。立足于队形优化研究背景，本节研究集群队形转换，目的在于解决集群利用盲区规避对方侦察或打击，如图7 所示。图中集群形成圆形疏散队形，通过对方侦察盲区（图中缺口处）时，需要形成密集队形进行隐蔽机动。同时，集群在面临任务调整时需要在机动过程中进行队形转换，例如从纵队式的战斗队形转换为圆形的侦察队形，如图8 所示。

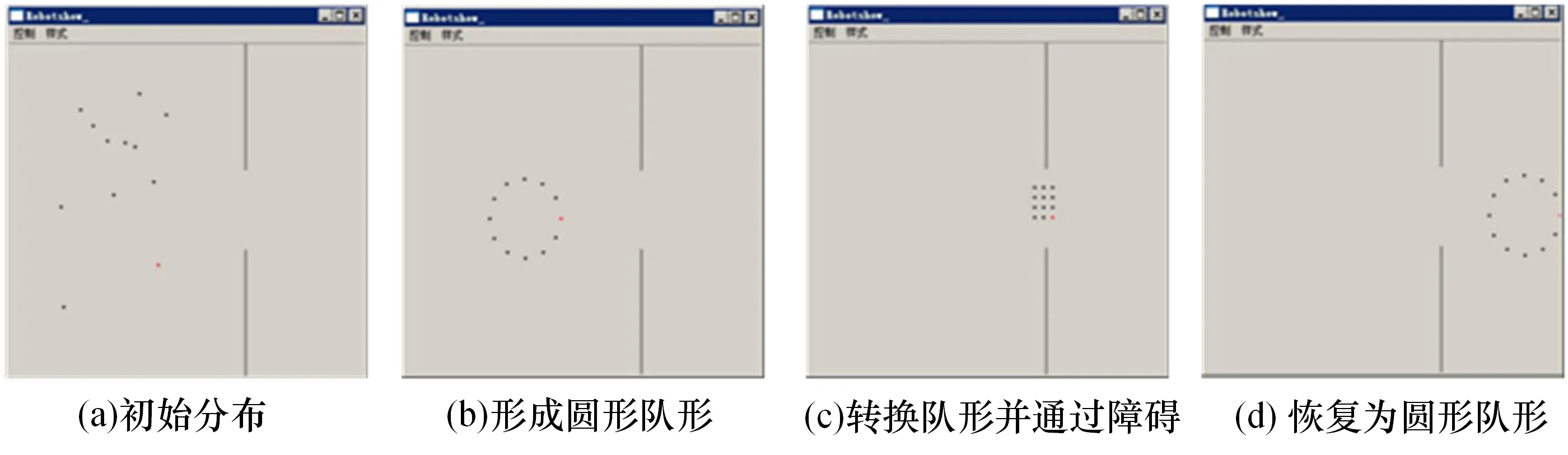
图7 “领导跟随”仿真结果（环境适应性）

图8 无人装备动态转化仿真

1.4 无人装备协同方式选择

上文介绍了基于队形控制的集群协同方法，落实到电子对抗力量运用层面，需要讨论协同方式的选择。有2 种序列生成方法，即自组织方法（A）和固定序列方法（F），对应的分别是有数据库索引和无数据库索引2 种方式。利用程序计算机动距离（可按照计算机屏幕尺寸比较）和时间，得到数据如表1-2 所示。可以看出，在数据库支撑下效率更高，这要求当前在大规模作战准备期间，加快无人装备协同方法研究，丰富战法数据库。利用EXCEL 软件可以将表格转化为图9。

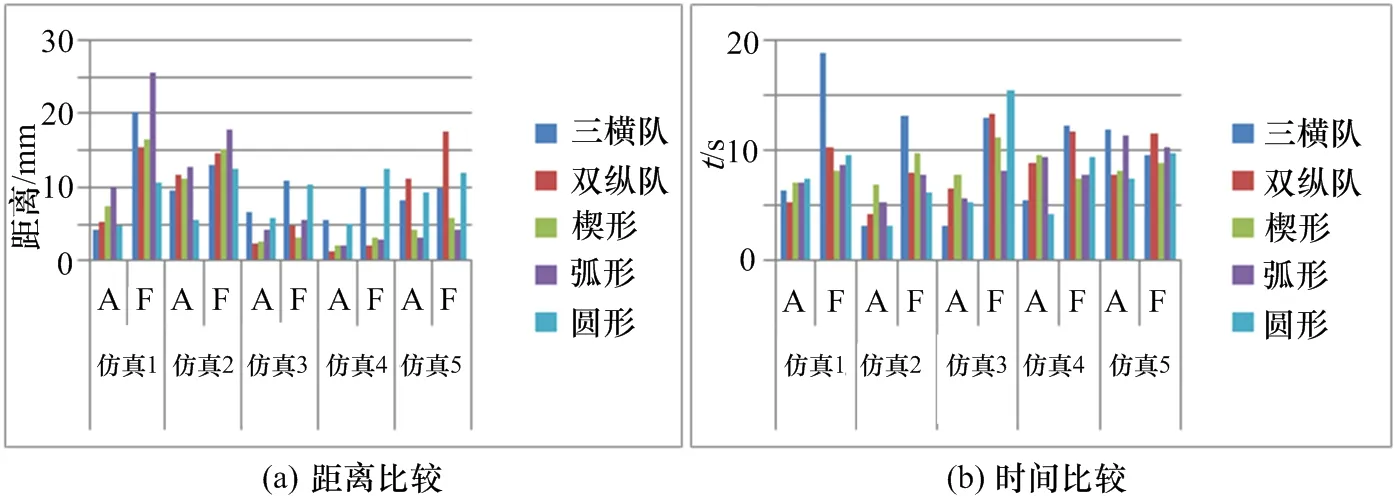
图9 “领导跟随”模式对比

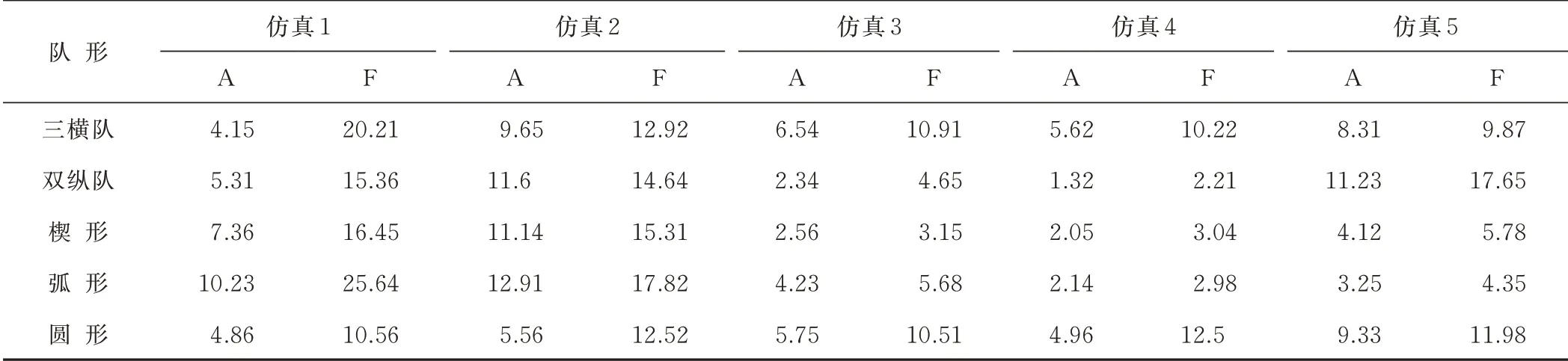
表1 “领导跟随”模式生成的A、F 队形的距离数据（一个基本单位：1 mm）

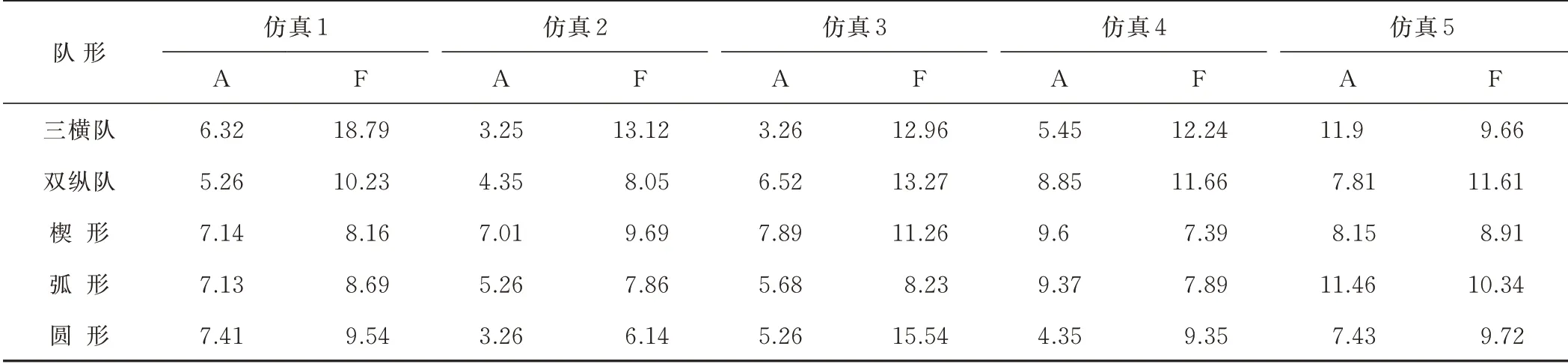
表2 “领导跟随”模式生成的A、F 队形的时间数据

2 “邻近引导”模式下集群协同方法

“领导跟随”模式属于基于“中心化”的协同方式，领航装备一旦失效，整个集群会失去控制。为此，提出了一种优化模式，即“邻近引导”，该模式等同于“领导跟随”模式，不同点在于选取的参考点不同。在该模式下，各无人装备实时位置的确定基点是其“邻近者”。所以算法重点是寻找每个无人装备的“邻近者”。同样为简化问题，首先先讨论F 类队形（无数据库索引）情况。

2.1 确定“邻近者”与队形生成

单线队形中，无人装备对称分布于→轴两侧，规定第个装备（序列号定义为）将第2 个装备作为“邻近者”。如果小于3，则“邻近者”为第1 个装备。多线队形中，的余数即为第个装备所在行数（），例如，0 时，第个装备就在第0 行。在第0 行可以通过求的值确定“邻近者”。≠0 时，则先求（+1）/2 的商，再求-的值，即为“邻近者”的序列号N。

确定“邻近者”后，需要从初始状态形成队形，方法同于“领导跟随”法。但需要在算法上做出优化：当0 位装备损坏后，后续装备依次担任0 位；当装备的非0 位“邻近者”损坏后，自动将损坏装备的“邻近者”作为新的“邻近者”。

2.2 无人装备协同与队形转换

确定好目标队形后，第1 个装备带领其他装备形成队形。在队形机动过程中，每一个装备都与其“邻近者”保持一定的距离，并且保持自身轴方向与向量→之间角度不变。向量→即为装备与其“邻近者”之间的距离向量。图10 对弧形队形进行演示，按照100 单位的速度和30°的舷角朝目标运动，在每个时节都进行点迹检验。

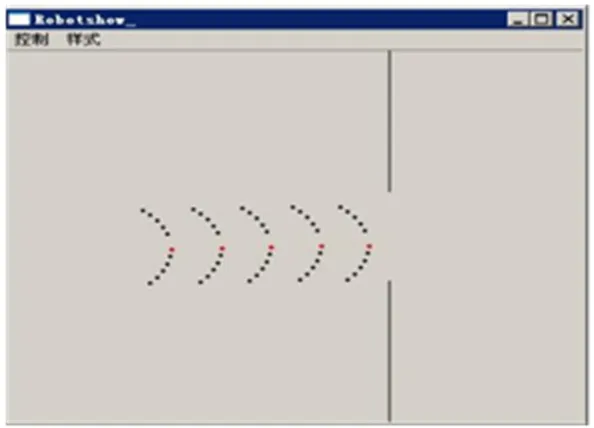
图10 弧形队形的集群协同仿真

利用仿真来演示集群利用“邻近引导”模式提高战场适应性。仿真距离为75 个单位，角度取15°。在机动过程中，遇到障碍或利用盲区机动时，能从疏散队形变换为密集队形，如图11 所示。

图11 基于“邻近者引导”的仿真

2.3 无人装备协同方式选择

同样对比自组织方法（A）和固定序列方法（F），利用程序计算机动距离（可按照计算机屏幕尺寸比较）和时间，得到数据如表3-4 所示。可以看出，在数据库索引下协同效率更高，更加验证了平时做好协同战法研究的必要性。图12 为表格转化图。

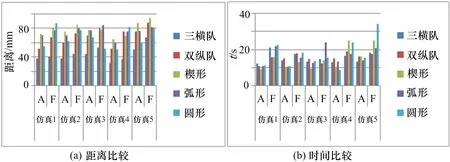
图12 “邻近者引导”方法模式对比

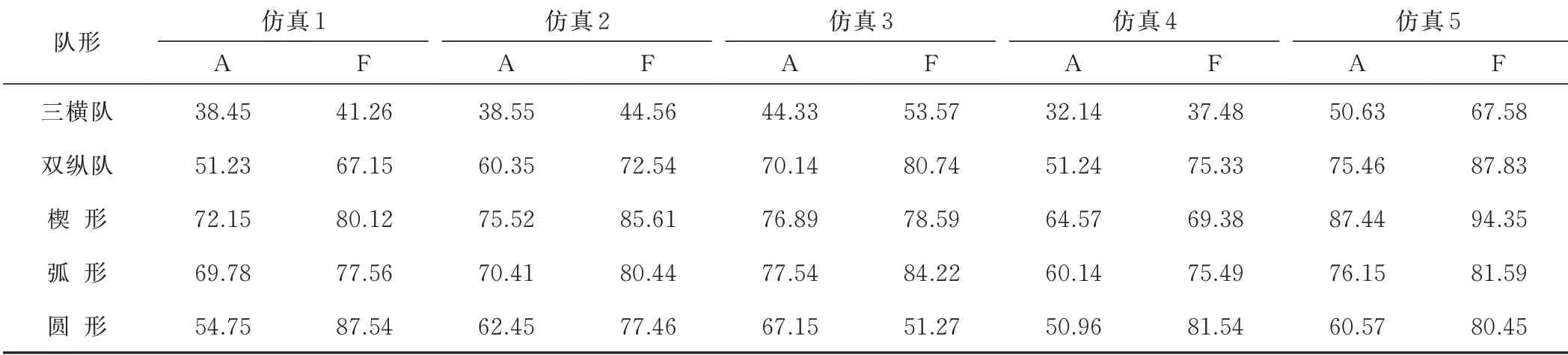
表3 “邻近者引导”方法生成的A 队形与F 队形的距离数据（一个基本单位：1 mm）

表4 “邻近者引导”方法生成的A 队形与F 队形的时间数据

对比图9、12，可以发现“领导跟随”时效性更高，所以在防空反导等对时间要求比较高的行动中，可以采取这种协同方式；而在抗海上袭扰时，由于目标抗毁性能大，对集群的抗毁性、稳定性要求更高，此时“邻近引导”协同可以发挥在不规则图形中保持固定间隔的优势，提高集群的稳定性。另外，还可以采取混合策略，例如，通过某电磁盲区前，基于“领导跟随”的集群变换成四路横队，此时四路横队的机动采取“邻近引导”方法，通过盲区后恢复队形。

3 结束语

本文主要对比了2 种队形控制方法在电子对抗智能体协同中的稳定性和时效性，其中稳定性参照的是形成队形的距离，遵循距离越短能耗越低、稳定性越高的先验准则。在衡量距离要素时，采用的是测量智能体集群的“领航者”或“零号”智能体在形成队形或转换队形时，在显示器上的位移。由于不同性能计算机影响，队形形成距离和时间差距较大，但对2 种队形的对比来说，影响较低，具有一定的参考价值。作为电子对抗指挥领域最复杂的问题，协同始终是推动电子对抗力量体系这一复杂巨系统效能发挥的驱动力，好的协同方法可以达成量变到质变的战场非线性态势转换。本文主要从数理层面进行了初步研究，而对于复杂系统理论中的突变和混沌等机理在电子对抗智能体协同中的表现还未深入探究。■