直升机红外诱饵干扰研究与仿真

向 宇，方 航

（中国船舶集团有限公司第七一〇研究所，湖北 宜昌 443000）

0 引言

红外制导导弹一直是各型武装直升机的最大威胁，保护直升机免遭红外制导导弹攻击是一个重大课题。原有的红外对抗手段已经落后，各国都在寻求新的红外对抗方法，一方面是研究新型红外干扰技术，另一方面是寻找红外对抗最佳战法。

红外导引头的发展经历了旋转扫描、圆锥扫描、十字交叉扫描和玫瑰花扫描，对这些红外制导导引头的干扰方式一般分为“隐真”和“示假”2 种。“隐真”是指消除红外目标的特征或使红外目标和背景的探测特征一致；而“示假”是通过制造假目标来干扰红外制导导引头，转移导引头对真实目标的注意力。目前“示假”的主要方法是通过释放红外诱饵进行干扰、迷惑和欺骗导引头，即质心式干扰。当一个或者多个红外辐射源存在于导引头红外视场范围内时，导引头不会只跟踪其中任意某个辐射源，而会跟踪所有辐射源形成的能量中心，这个能量中心通常被称为质心。通常的干扰策略是增加红外诱饵投放数量，形成多方位、高密度、大空域覆盖，增加导引头识别载机的难度，提升载机逃离概率，但该策略效费比很低。相比于战斗机，直升机的负载能力一般不高，无法携带大量红外诱饵，所以并不适用该策略进行作战，需要寻求更加适用于直升机的干扰策略。

红外诱饵的性能指标包括投放速度、光谱特性、辐射强度、上升时间、持续时间和气动特性。基于这些指标，本文对投放压制比、投放时间间隔、投放时机和载机机动方向进行了理论分析并给出了结论，最后通过仿真实验对理论分析结论进行了验证和改进。

1 机载点源红外诱饵干扰原理[7-9]

导引头接收到的红外诱饵的红外辐射强度只要大于直升机，质心就偏向诱饵，即导引头视场中心线偏向诱饵。随着时间推移，当诱饵和直升机距离拉大后，由于该中心线是偏向诱饵的，直升机就会越来越靠近导引头视场范围的边缘，只要诱饵的持续时间够长，直升机就会脱离导引头视场范围。反之，如果直升机的红外辐射强度大于诱饵，质心就会偏向直升机，即中心线偏向直升机，诱饵反而会先于直升机脱离导引头视场范围。所以实现红外干扰的必要条件是导引头接收的诱饵辐射强度大于直升机。辐射强度质心的计算如式（1）所示：

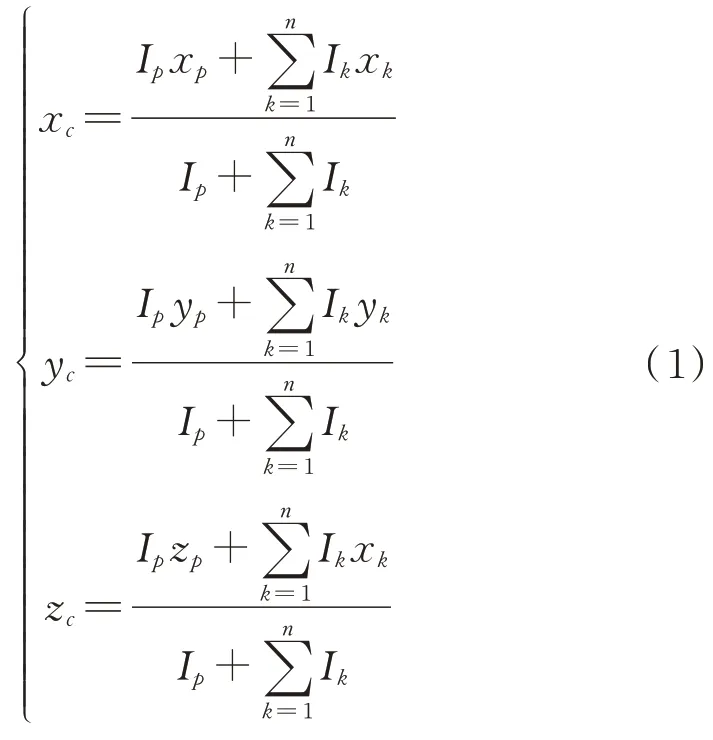
式中，x、y、z代表质心位置，I是直升机的红外辐射强度，x、y、z是直升机的空间坐标，I是第发诱饵的红外辐射强度，x、y、z是第发诱饵的空间坐标。

通过式（1）获得的质心位置如图1 所示，可以看到由于导引头跟踪质心，飞机脱离了导引头视场范围。

图1 红外质心示意图

2 干扰策略研究

研究直升机红外诱饵干扰投放策略的目的，是为了避免像传统战斗机那样通过大量的红外诱饵投放来实现干扰，所以需要对一些关键的投放指标进行分析，力求发挥诱饵的最大效用，在提升诱饵干扰成功率的同时尽可能地减少诱饵投弹量。为了构建这种策略，下面对一些相关投放指标进行分析和推导。

2.1 诱饵弹投放时机

用诱饵进行干扰的过程如图2 所示，图中t是投放装置的响应时间，t是从投放到点火的时间，t是从点火到额定功率的时间，t是大于额定功率阶段的持续时间。

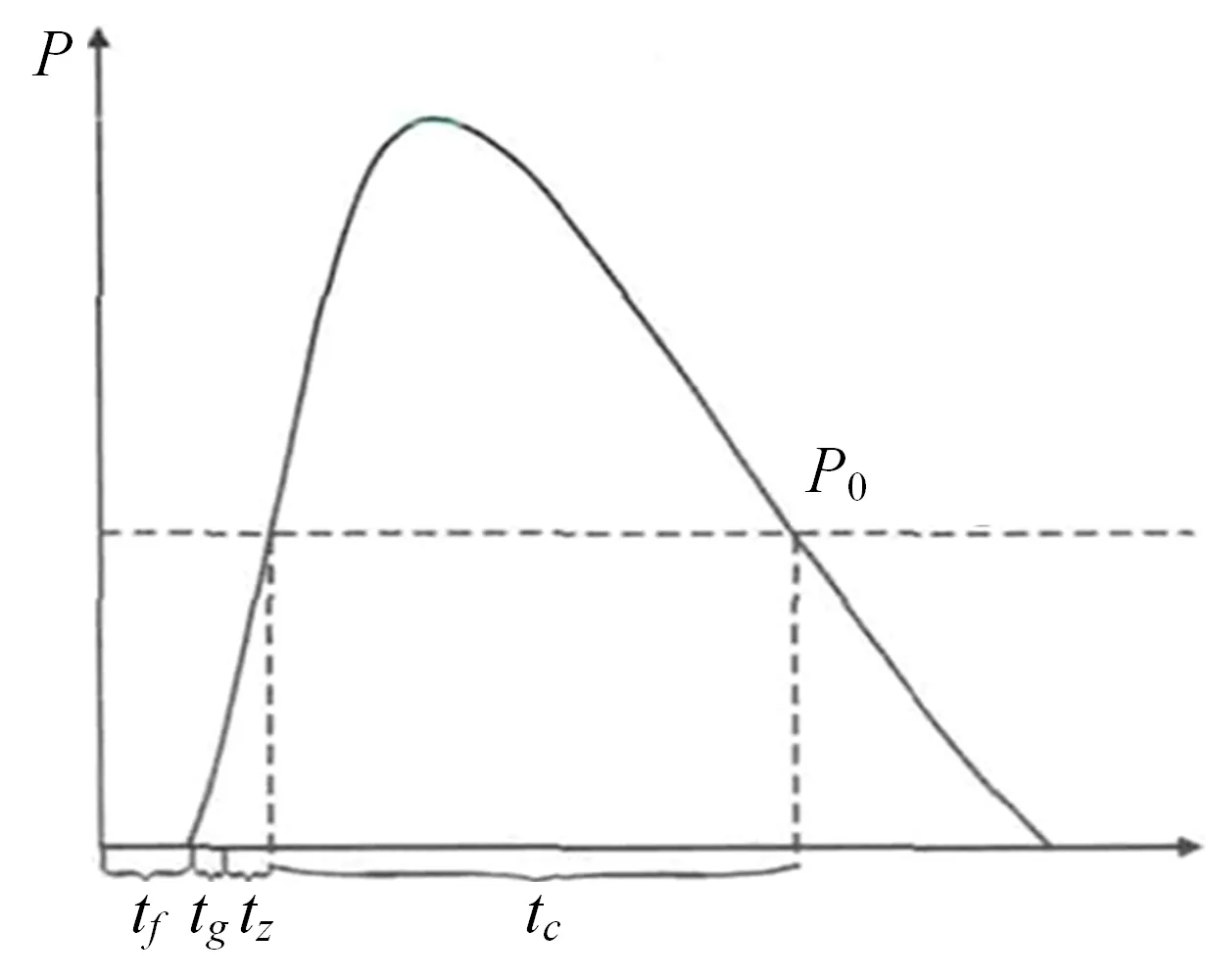
图2 诱饵干扰过程示意图

下面以尾向攻击的红外制导导弹为例说明红外诱饵不同持续时间对应的弹机距离。令诱饵的发射方向与直升机的飞行方向垂直，且与垂线间的夹角为。令为诱饵不同持续时间下质心干扰对应的最大距离。该距离和导弹、直升机以及诱饵需要满足：

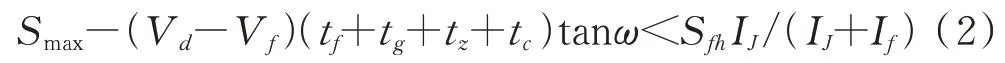
式中，是导引头半视场角，V是导弹的飞行速度，V是直升机的飞行速度，S是诱饵从发射到额定辐射功率时诱饵和直升机之间的距离。S可由式（3）计算：

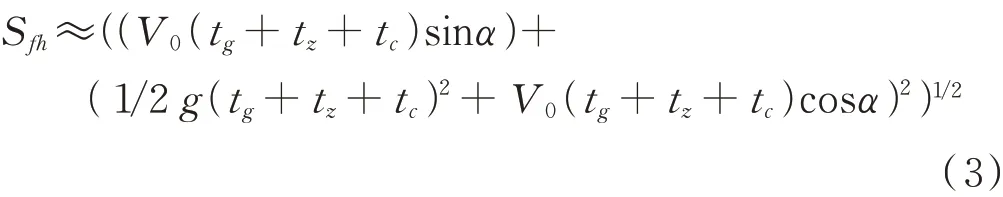
式中，是诱饵发射速度，是重力加速度。由式（2）—（3）算出诱饵持续时间和最大作用距离间的关系如表1 和图3 所示。

表1 诱饵持续时间和最大作用距离关系

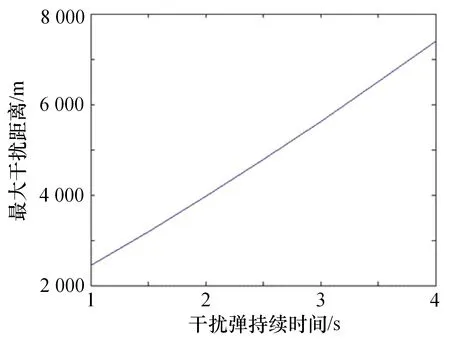
图3 诱饵持续时间和最大作用距离间的关系

当大于表1 中距离时，诱饵的辐射功率会降到额定功率以下，此时直升机还在导引头跟踪视场范围内，即发射一枚红外诱饵可能无法干扰成功，需要发射第二枚诱饵。

另外，存在红外诱饵先于直升机飞出导引头视场范围的情况，即诱饵发射时导弹距直升机太近，诱饵在到达额定功率前就飞出了导引头视场范围，仿真实验中就存在这种案例。为了更好地了解诱饵应用范围，需要考虑诱饵发射时的最小弹机距离。该距离是指经过发射和上升时间后，诱饵依然能够存在于导引头视场范围内的距离最小值。令诱饵从点火到发射的时间为t，上升时间为t，诱饵坐标为C()，直升机坐标为C()，导弹坐标为C()，直升机、诱饵间距为S(C,C)，直升机、导弹间距为S(C,C)，导引头视场角为。为了诱饵能够发挥干扰作用，在经过t+t时间后，直升机、诱饵间距与直升机、导弹间距需满足：

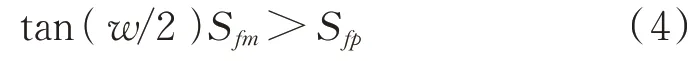
用尾追举例，即=(V-V)(t+t)。显然，在尾追情况下，诱饵弹最小发射弹机距离是所有情况下是最大的，当无法实时解算最小弹机距离或不需要知道精确的最小弹机距离时，可以将该距离作为发射的最小弹机距离。

2.2 压制比

该指标和诱饵红外辐射强度及载机红外辐射强度相关，从数据上反应了诱饵能发挥的诱偏程度。但考虑到实际情况，压制比无法做到无限大，所以需要选择一个合适的压制比值。压制比、作战需要的导弹诱偏程度、抗干扰系数和诱饵及直升机的辐射强度具有如式（5）所示的函数关系：

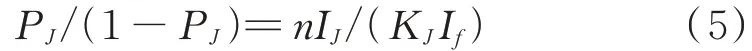
式中，表示压制比；K表示导引头抗干扰系数；I表示诱饵弹辐射强度；P表示需要的导弹诱偏程度；I是直升机的红外辐射强度。当P确定后，就可以计算压制比，如式（6）所示：

绘制出式（6）的曲线图如图4 所示。可以看到当压制比为2 时，诱偏程度的增长率达到了峰值，而当压制比为4 时，诱偏程度的增长开始大幅减缓。所以，压制比取2 时诱饵效费比最高，最大取4，再大就没有意义了。

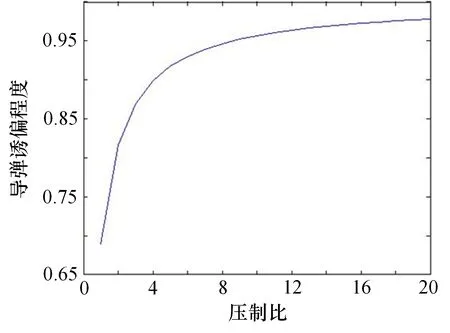
图4 压制比的诱偏效果示意图

2.3 投放间隔时间

诱饵的投放间隔时间也是决定诱饵弹使用效率的重要指标。投放间隔时间越长，单枚诱饵弹发挥的效用越高。但在一枚诱饵无法完成干扰时，过长的间隔可能导致诱饵飞出导引头视场范围时，直升机还处于视场范围内。这种情况下导弹会重新跟踪直升机，该枚诱饵的干扰效果就完全被导弹屏蔽掉了。另一方面，过短的间隔虽然能保证导引头不会重新跟踪直升机，但对诱饵的使用效率偏低。而且过于密集的诱饵投放会将导引头跟踪视场中心线从偏向距离最远的诱饵拉向直升机，当导弹靠近直升机时会由于视场范围内新发射的诱饵到达额定功率需要时间而直接跟踪载机。所以，不能简单地设置过长或过短的投放间隔，需要寻找一个合适的投放间隔时间。如果一枚诱饵弹无法完成诱偏，直观上来说最佳投放间隔时间是前一枚诱饵在飞出导引头视场范围时下一枚诱饵达到额定功率。假设起燃时间为0，则上述最佳投放间隔时间变为前一枚诱饵即将飞出导引头视场范围时投放下一枚诱饵。图5 中导弹在时直升机投放第一枚诱饵。

图5 最佳投放时间间隔示意图

导弹到达时，如果诱饵位于视场边缘，由三角形近似性可得：

式中，φ为导引头视场角，为红外诱饵到质心的距离，为导弹来袭角度，为诱饵和导弹间距。

由式（7）可知诱饵的最佳投放间隔时间∆需满足：

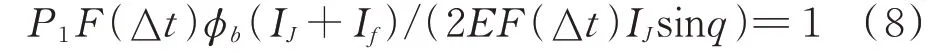
有一种情况是不考虑上述投放间隔时间的，如果来袭距离较大，投放间隔时间将会很大，这是因为该式没有考虑诱饵持续时间，所以对投放间隔时间需要取一个上限。考虑当直升机还在导引头视场范围中时，应时刻有诱饵对导引头做出干扰。所以这个合理的上限应是第一发诱饵的辐射功率降到额定辐射功率时，第二枚诱饵的辐射功率刚好上升到额定辐射功率，也就是一枚红外诱饵的持续时间t。所以诱饵的投放时间间隔如式（9）所示：

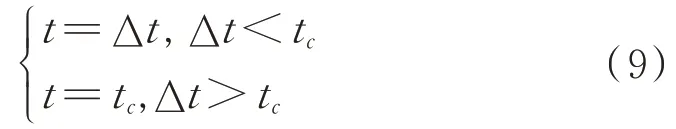
所以，如果能获得足够数据并实时计算出诱饵到达导引头视场边缘的时间，就以该时间作为精确投弹时间间隔。如果无法计算该时间，则以诱饵弹额定功率持续时间为投弹间隔时间。

诱饵弹被飞机投放后，主要受到重力和空气阻力。定向上为速度正方向。假定飞机飞行的速度为，飞机的俯仰角为，诱饵弹初速度为, 垂直飞机飞行方向投放。假设诱饵弹出膛后发生燃烧反应的质量为，诱饵弹的受力情况如式（10）所示：

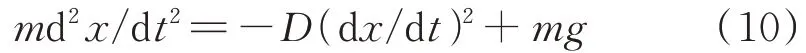
将式（10）用速度导数表示：

式中，为重力加速度，为空气阻力系数，=/2。

干扰弹水平方向速度变化如式（12）所示，式（13）是该式的解析解。

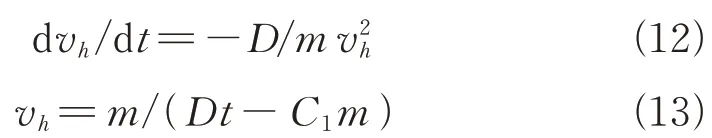
最终可推导出飞机俯仰角大于等于0 和小于0 时的水平方向速度，如式（14）和式（15）所示：

当≥0 时，在=0 时刻

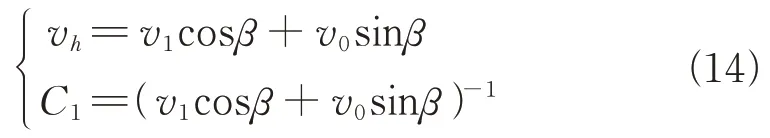
当＜0 时，在=0 时刻

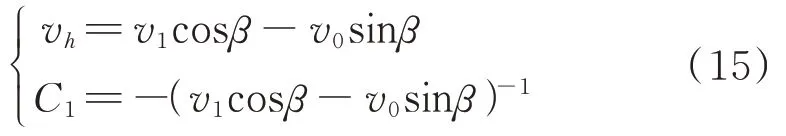
根据式（14）、（15）绘制出诱饵水平速度变化，如图6 所示，可看出诱饵在水平方向的速度是快速趋向于0 的。

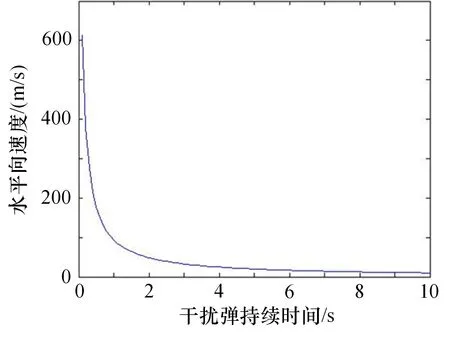
图6 诱饵水平速度变化示意图

接下来推导诱饵垂直速度。当＞0 且sincos＞0 时，干扰弹的飞行分上升段和下降段，诱饵在垂直方向的速度受力如式（16）所示：

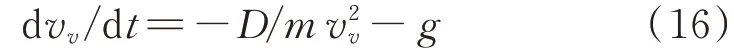
解式（16）可得：

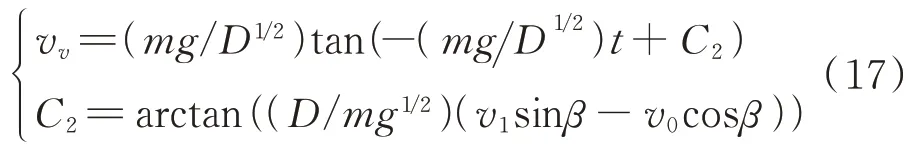
当干扰弹飞行至最高点时，v=0，此时=(/)/。当≥(/)/时，干扰弹的飞行处于下降段，有：

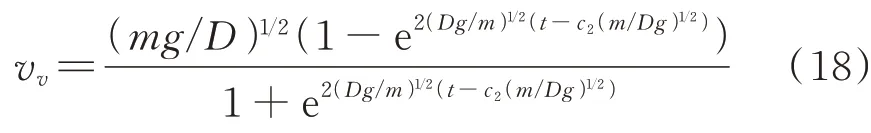
当||cos-||sin＞0 时，得到干扰弹垂直地面方向的速度变化为：

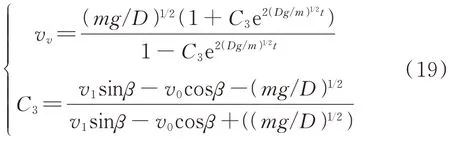
垂直速度变化如图7 所示，由图可知垂直方向速度由于空气阻力和重力，最终将趋于匀速运动。

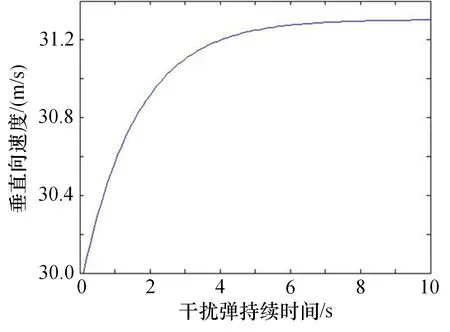
图7 垂直方向速度变化示意图

整个诱饵的运动轨迹如图8 所示。

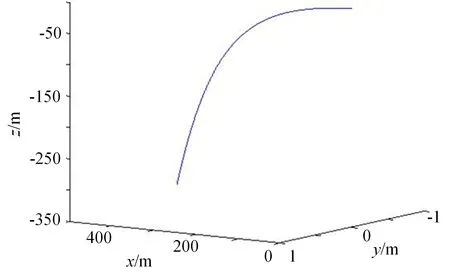
图8 诱饵运动轨迹示意图

由诱饵运动相关计算式和投放间隔时间相关计算式可算出诱饵的最佳投放间隔时间在[0.3 s,4 s]范围内，如果红诱饵的持续时间t小于4 s，则最佳投放间隔时间在[0.3 s，t]范围内。图9 是针对不同来袭距离和来袭俯仰角计算的诱饵最佳投放间隔时间。

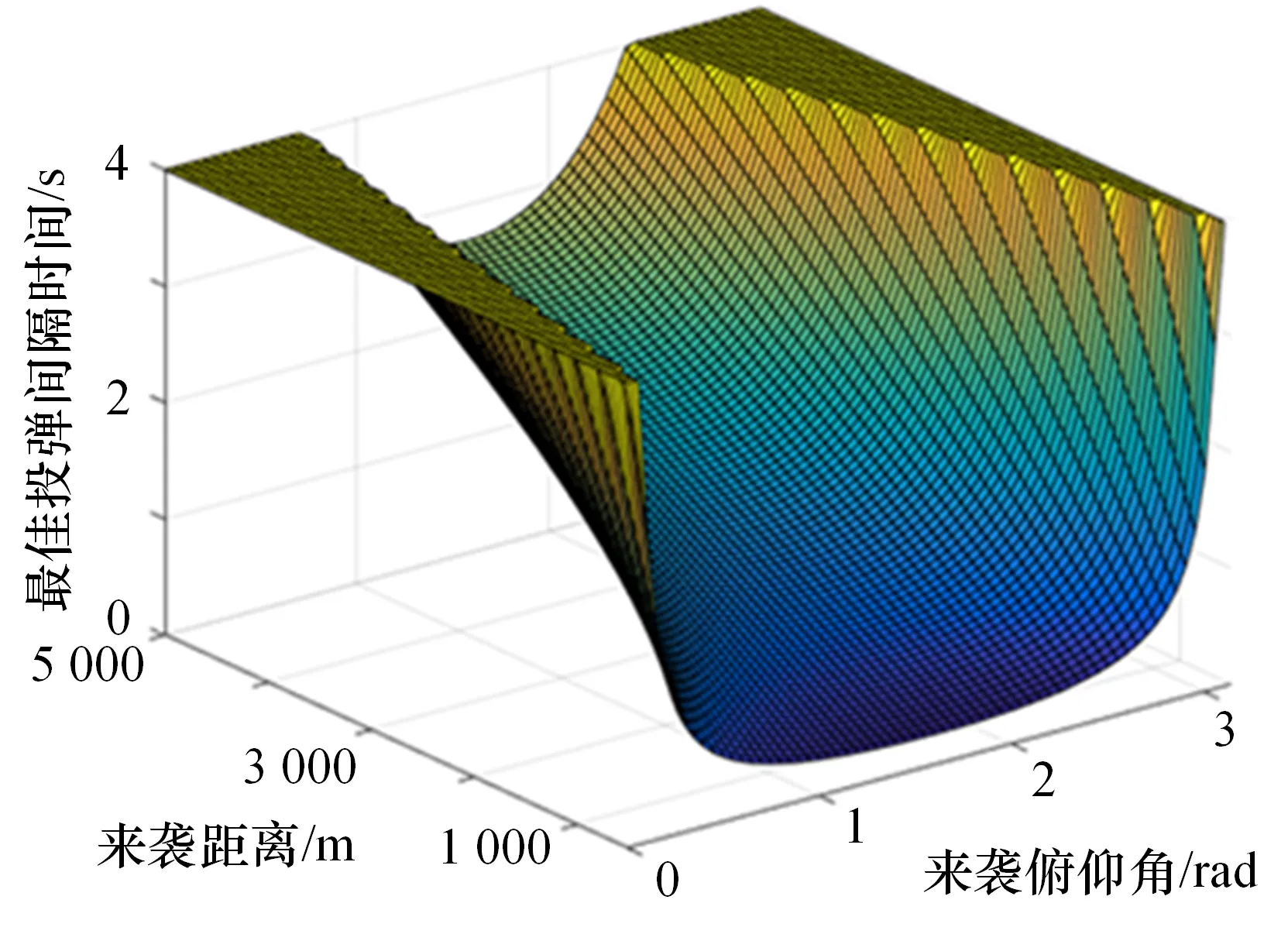
图9 不同来袭距离俯仰角下的投弹时间间隔

2.4 机动方向

在最后一枚诱饵弹有效的情况下，即诱饵投放时的导弹和直升机距离大于最小弹机距离，此时直升机、诱饵在导弹处的红外辐射强度与它们和导弹的距离成正比。所以，提升直升机逃脱成功率的关键就是使直升机对导引头的红外辐射强度增长率为负。机动的方向就是使直升机和导引头的距离增长率为最大负值的方向。

3 仿真实验及数据分析

该仿真实验主要在VTR32-EG7 平台上进行，分别针对压制比和投弹间隔时间进行了2 组实验。在进行压制比选取实验时，主要是为了验证前文的理论分析结论，即压制比为2 时的效费比增长速率最高以及压制比为4 时基本达到最大诱偏性能。而进行投弹间隔时间实验则是为了从理论分析的投弹间隔时间区间范围内寻找最佳投弹间隔时间。

3.1 压制比实验

该实验中分别测试了压制比为1、2、3、4 四种情况时的诱饵干扰成功率。对于每种压制比，本文都测试了不同来袭方位角和来袭距离下的诱饵干扰成功率。来袭方位角的测试范围是[0°，180°]，步长20°，即选取从迎头到追尾共10 个来袭方位角，来袭距离的范围是[500 m，5 000 m]，步长500 m，共10 个来袭距离，投放间隔时间取诱饵达到额定功率后的持续时间。每种压制比分别进行了100 次干扰仿真实验。图10 是四种压制比下干扰仿真实验的结果。

图10 中深蓝色方块代表干扰完全失败导弹正中直升机的毁伤中心，褐红色代表导弹被诱骗至完全脱离毁伤半径范围。其它颜色越接近深蓝色表示越接近毁伤中心，越接近褐红色表示越远离毁伤中心。由实验结果可知，压制比为2 时诱饵干扰效果确实比压制比为1 时有了明显提升。而压制比为4 时基本对于所有情况都能干扰成功。通过观测失败的实验录像，本文发现当直升机比诱饵弹更快接近导引头时，导引头将不再按照诱饵弹发射时设置的压制比进行视线偏转，会更多地偏向直升机，诱饵弹会先出导弹视场角。造成这一现象的原因应该是导引头端直升机辐射强度提升速率高于诱饵。对于500 m 来袭距离，所有压制比实验均干扰失败，这说明由于距离太近，可能因诱饵达到额定功率需要时间或者导引头在500 m距离时已经进入惯导阶段而无法进行干扰。

图10 四种压制比下干扰仿真实验的结果

3.2 投放间隔时间实验

该实验中分别测试了投放间隔时间为0.5 s、1 s、2 s、3 s 四种情况下的诱饵干扰成功率。对于每种投放间隔时间，本文测试了不同来袭方位角和来袭距离下的诱饵干扰成功率。来袭方位角的测试范围是[0°，180°]，步长20°，即选取从迎头到追尾共10 个来袭方位角，来袭距离的范围是[500 m，5 000 m]，步长500 m，共10 个来袭距离。在3.1 节的压制比实验中，当压制比取3、4 时，诱饵干扰基本都成功了，所以压制比取3或4 可能无法很好地体现投弹间隔时间对干扰成功率的影响。同理，压制比也不能取1。另外，从理论分析和3.1 的实验结果也可以看出效费比最大的压制比为2，最具实际意义。所以，在本实验中压制比固定为2。对每种投弹间隔时间进行了100 次实验。图11 是四种投弹间隔下的干扰仿真实验结果。

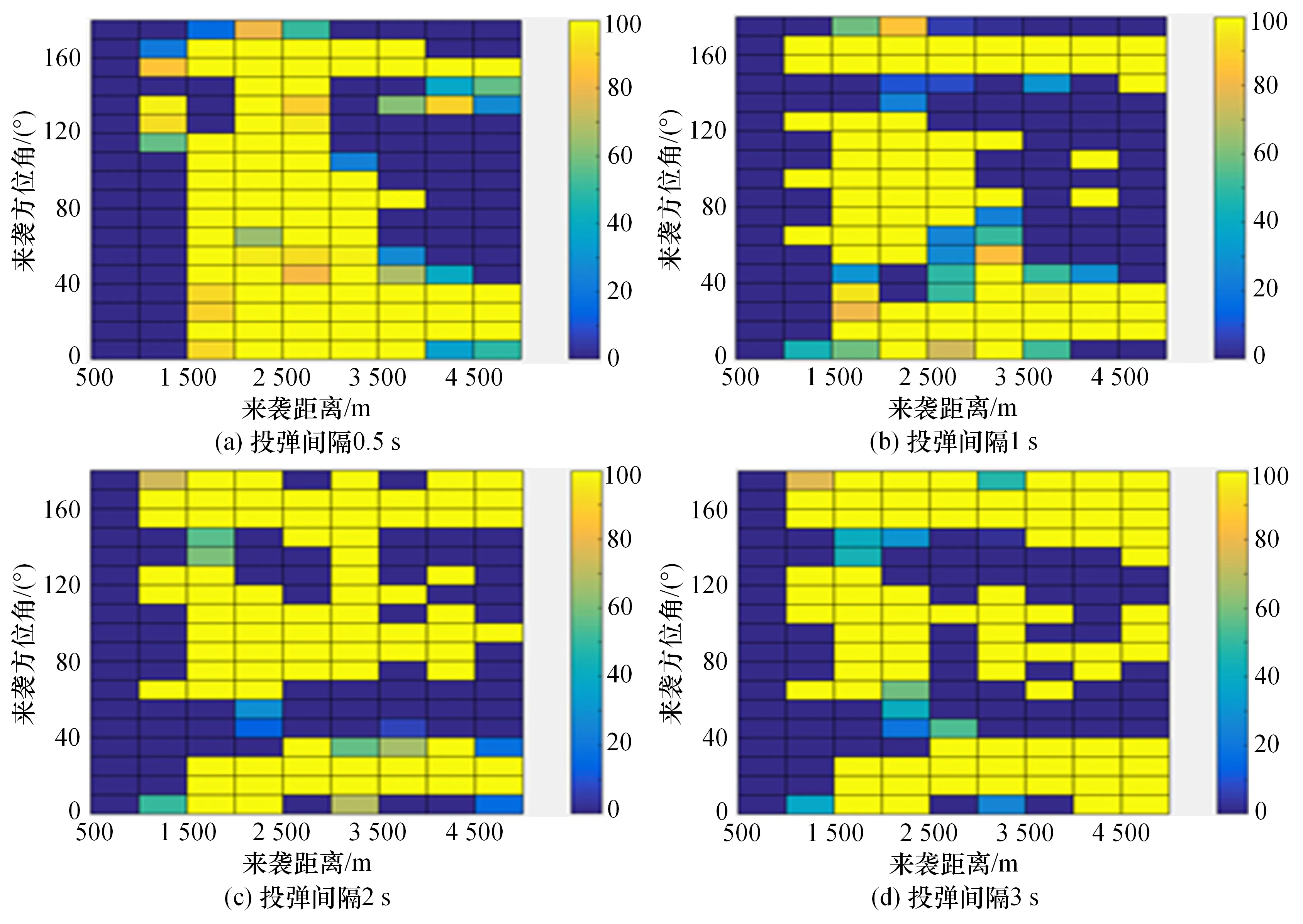
图11 四种投弹间隔下的干扰仿真实验结果

图11 中深蓝色方块代表干扰完全失败导弹正中直升机的毁伤中心，明黄色代表导弹被诱骗至完全脱离毁伤半径范围。其它颜色中越接近深蓝色表示越接近毁伤中心，越接近明黄色表示越远离毁伤中心。由上述仿真结果可知，在0.5 s、1 s、2 s、3 s 投弹间隔下的干扰成功率大体相同，说明在无法实时精确计算诱饵弹运动至导引头视场边缘的时间时，无法找到近似最优解。所以，根据前面的理论分析和3.1 节压制比实验结果可知，此时以诱饵的持续时间为投弹间隔时间即可。

4 结束语

本文从现有点源红外诱饵干扰原理入手，通过诱饵、飞机和导弹的一些性能指标研究了诱饵弹的最大作用距离和最小投放距离，通过这些距离可以进行投放时机和投放枚数的选取。另外，本文对投放策略中的重要指标压制比、投放间隔时间以及机动方向进行了理论分析，推导出相应结论。最后，本文通过实验验证了这些结论的合理性，对直升机红外诱饵投放策略具有极大的参考价值。当然，本文限于作者的理论水平及仿真平台性能，还存在很多缺陷和不足，这些将是进一步研究的方向。■