油纸绝缘混联模型含水率定量评估参数的提取及研究

林朝明，林超群，叶晨欣，叶 荣

（1.福建水利电力职业技术学院 电力工程学院，福建 永安 366000；2.国网福建省电力有限公司超高压分公司，福建 福州 350009；3.国网福州市长乐区供电公司，福建 长乐 350200；4.国网福州供电公司，福建 福州 350009）

0 引言

当前，以油浸式变压器为代表的电气设备的稳定运行对构建一个可靠、优质的电网具有重要意义。由绝缘纸和绝缘油组成的复合绝缘系统是该类设备内绝缘的典型结构[1]，而复合绝缘系统受潮老化会严重影响设备的稳定运行[2]。在绝缘介质受潮老化的过程中，水分既是产物，同时又对老化过程起到促进作用，此外，在水分平衡条件下，绝缘纸中的水分含量是绝缘油中的104倍[3]。因此，对设备绝缘纸含水率的准确评估成为了保障电网可靠运行的关键问题之一[4]。

近年来，对油纸绝缘设备进行状态评估的介电响应方法有回复电压法（recovery voltage method，RVM）、极化去极化电流法（polarization and depolar‐ization current，PDC）以及频域介电谱法（frequency domain spectroscopy，FDS）[5-7]。 其 中 ，RVM 法 和PDC法由于测量设备的最高采样频率限制，使得时域谱线在高频部分的测量精度较低，加之时域小信号易受到噪声干扰，两者的测量结果总体误差较大，使其现场应用受限较大。而FDS法测试所得的曲线携带丰富的油纸绝缘信息，且易于实现实验室数据与现场测试数据之间的对接[8-9]，因此FDS成为了当前的研究热点。

在FDS的应用方面，基于等效模型分析绝缘介质受潮状态的方法因建立在电介质微观介电行为之上，使得模型参数具有明确的物理意义，有助于建立起绝缘介质受潮状态与参数间的数学联系。当前广泛采用的模型是扩展Debye模型及其优化模型，如Cole-Cole模型、Davidson-Cole模型及Havril‐iak-Negami模型[10-12]等，所描述的对象均是单一介质的弛豫极化过程[13]，而电气设备的绝缘信息往往十分复杂，简单的R-C等效支路难以确切描述油纸绝缘系统的多种极化过程。

鉴于此，本文立足于油纸绝缘混联模型——一种在扩展Debye模型基础上引入界面极化支路的拓扑结构，首先结合FDS实测数据对模型极化支路数的多种取值情况进行讨论，确定最贴近实验室条件与现场测试环境下油纸绝缘实际弛豫极化过程的极化支路数取值范围；然后采用FDS实验数据与实测数据相结合的方式，重构数据在两个不同等效模型下的FDS计算值曲线，通过吻合度法可以直观反映两个模型在表达绝缘纸受潮介电响应信息的差异，凸显混联模型拓扑结构的优势；最后在有效分析绝缘纸含水率对模型参数影响规律的基础上提取模型各支路中对水分敏感的特征参数，通过建立拟合方程实现绝缘纸含水率的定量评估。

1 混联模型极化支路取值范围的确定

1.1 油纸绝缘混联模型

现有研究表明，油纸绝缘系统受潮老化后其内部存在的极化过程主要为电子位移极化、偶极子转向极化、界面极化[14]。其中界面极化所描述的是具有不同电导率的夹层介质在外施电场作用下界面空间电荷的生成及聚集现象，其极化速度与两种介质的电导率、相对介电常数相关[15]。为更加真实地反映绝缘介质的极化响应特性，本研究引入油纸绝缘混联模型[16]，其拓扑结构如图1所示。其中，绝缘电阻Rg、几何电容Cg构成了几何电路，m条Rsm-Csm串联组合所构成的极化支路反映单一介质的弛豫特性，M条CiM、Ri(2M-1)、Ri2M所组成的界面极化支路表征油纸绝缘系统的界面极化过程。

图1 油纸绝缘混联模型Fig.1 Hybrid model of oil-paper insulation

由图1可知，与扩展Debye模型相比，该模型增添了界面极化支路，该支路的时间常数不仅取决于CiM、Ri(2M-1)，还与Ri2M密切相关，因此混联模型理论上蕴含的介质极化响应特性信息更丰富。模型参数分析作为一种探索绝缘介质极化响应特性行之有效的手段，本研究将聚焦于混联模型参数的有效求取及深入分析，以进一步说明该模型的优越性。

由图1可得油纸绝缘混联模型导纳方程Y(w)为式（1）。

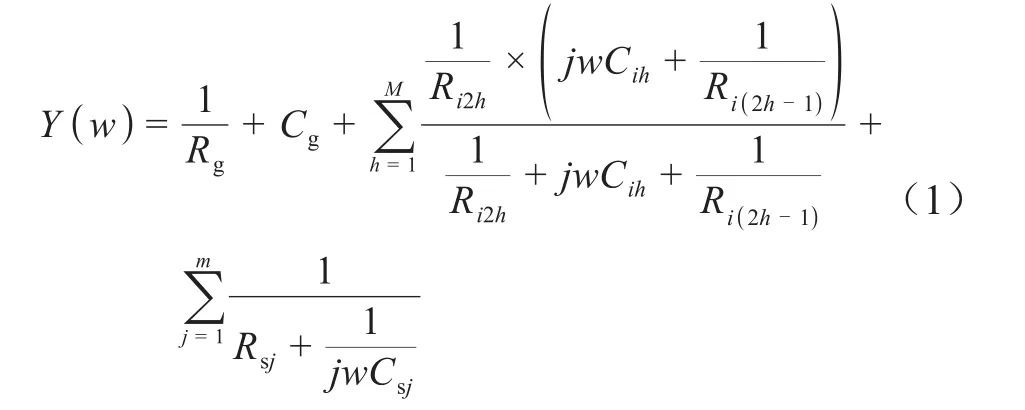
式（1）中：i=1,2,…,M；j=1,2,…,m；Ri2h、Ri(2h-1)、Cih、Csj为模型支路的等效电阻与电容；w为测试频率。

1.2 频域混联模型的参数求取

从理论上解释电介质的微观介电过程是油纸绝缘介质响应等效模型的最基本用途，为使建立的模型具有一定的实用价值，需结合频域介电响应数据进行模型的参数估计。

首先，根据需要建立一组只包含C'(w)、C"(w)的非线性方程组，如式（5）所示。

式（5）中：wj为FDS测试的角频率；C'实测(wj)、C″实测(wj+1)分别为FDS实测的复电容实部、虚部值；C'求取(wj)、C″求取(wj+1)分别为模型中待求取的复电容实部、虚部值。

其次，建立总体优化目标函数，如式（6）所示。

式（6）中：k为FDS采样次数；w1i、w2i为权重值，令w1i=1/C'实测(wi)，w2i=1/C''实测(wi)。

最后，采用自适应收缩因子粒子群算法[17]对式（6）进行迭代求取，当f(w)接近0时，便获得了最优解。

1.3 极化支路（m，M）不同取值分析

由图1可知，不同取值的（m，M）会产生不同个数的混联模型参数，要有效辨识模型参数，必须先确定（m，M）的具体取值范围。

图2为两台感应调压器（均已退役）的FDS实测数据，以型号为TSJA-20/0.5的数据为基础，结合吻合度法获取能够精准反映绝缘纸受潮时介电响应信息的极化支路数取值情况。

图2 感应调压器FDS现场测试数据Fig.2 FDS test data of induction voltage regulator

参数吻合度W的计算方法如式（7）所示。

式（7）中：li实测为FDS第i次采样点的测试值；li计算为同一频率下依据式（3）～（4）得到的计算值。

目前，就等值电路的极化支路数取值情况学者们已展开一定的研究，发现3～7条极化支路能较准确地描述不同受潮老化状态下变压器油纸绝缘系统的弛豫极化过程[18]。按照混联模型极化支路的多种取值情况，依据TSJA-20/0.5感应调压器数据求取得到的各参数吻合度如表1所示。由表1可以发现：

表1 TSJA-20/0.5的各参数吻合度Tab.1 Consistency of parameters of TSJA-20/0.5

（1）M+m越小，频域介电量的吻合度越低，这是因为所测试的感应调压器为已退役的油纸绝缘设备，其内部绝缘受潮老化严重，由此产生的介电响应较复杂，需要多条极化支路来表达内部的微观介电响应过程；

（2）当M大于m时，频域介电量的吻合度均出现负数的情况，这是由于此时的参数辨识结果远超过实测值，由式（7）可知会出现吻合度小于0的情况；考虑到所测试的感应调压器具有较为复杂的介电弛豫极化过程，由此可说明混联模型中一般只需添加较少数量的界面极化支路，R-C串联极化支路在极化支路总数中所占的比重应较大；

（3）当（M+m）为5～7时，M大于m除外，参数辨识效果较好，特别是当M+m=6时的吻合度更高；同时在M+m=6中，当m=4，M=2时，3个频域介电量实测值与计算值的吻合度最高。

2 混联模型与扩展Debye模型的对比

为证明混联模型相较于扩展Debye模型能更真实地反映油纸绝缘系统复杂的介电响应，基于不同测试环境下的FDS数据进行两个模型的参数辨识，对两个模型的实测曲线与计算曲线吻合度情况进行分析。

2.1 基于实验数据的两模型对比

参照文献[19]中方法进行不同含水率油纸绝缘样品的制备，实验材料为25号环烷基矿物油及普通纤维绝缘纸板，采用高精度电子称获取纸中水分含量，测试结果如图3所示。

图3 不同含水率油纸绝缘样品的FDS测试结果Fig.3 FDS test results of oil-paper insulation sample with different water content

选取含水率为3.63%的测试数据，进行两个模型未知参数的求取，且保持两模型的极化支路总数一致。混联模型参数的求取结果如表2～4所示，扩展Debye模型参数的求取结果如表5～6所示。

表2 含水率为3.63%样品的混联模型中Rg、Cg计算结果Tab.2 Calculation results of Rgand Cgin hybrid model of sample with 3.63% of water content

表3 混联模型中界面极化支路参数计算结果Tab.3 Calculation results of interface polarization branch parameters in hybrid model

表4 混联模型中R-C串联极化支路参数计算结果Tab.4 Calculation results of R-C series polarization branch parameters in hybrid model

表5 含水率为3.63%样品的扩展Debye模型中Rg、Cg计算结果Tab.5 Calculation results of Rgand Cgin extended Debye model of sample with water content 3.63%

表6 扩展Debye模型中R-C串联极化支路参数计算结果Tab.6 Calculation results of R-C series polarization branch parameters in extended Debye model

基于表2～6中的结果重构FDS曲线，并与实测曲线进行对比，所求得的吻合度如表7所示。

由表7可以看出，经混联模型重构FDS曲线后的实测值与计算值吻合度均高于扩展Debye模型，说明基于实验频域介电数据的FDS辨识混联模型参数效果优于扩展Debye模型。

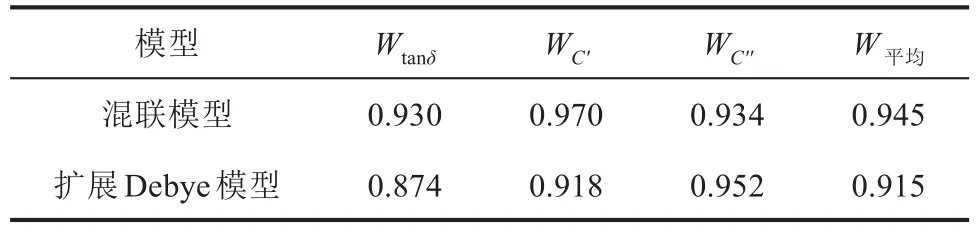
表7 不同模型下重构FDS曲线的吻合度对比Tab.7 Comparison of consistency of reconstructed FDS curves under different models

2.2 基于油纸绝缘设备测试数据的两模型对比

通过2.1节可知，两模型的差距不是十分明显，这主要是因为测试样品的介电响应过程相较于油纸绝缘设备而言较为简单。为此，以图2中TSJA-30/0.5感应调压器的测试数据进一步说明两模型在表达油纸绝缘系统介电响应信息上的差异。

由1.3节的分析，当（M+m）为5～7时谱线的吻合度均可达到0.85以上，因此对TSJA-30/0.5的参数辨识应考虑（M+m）为5～7时所有可能的情况，最终取吻合度最高的参数辨识结果。根据TSJA-30/0.5的FDS数据，混联模型的参数求取结果如表8～10所示，扩展Debye模型的参数求取结果如表11～12所示。其中混联模型的极化支路总数为5，m、M的取值分别为3和2，因而扩展Debye模型的极化支路总数与混联模型保持一致。

表8 TSJA-30/0.5的混联模型中Rg、Cg计算结果Tab.8 Calculation results of Rgand Cgin hybrid model for TSJA-30/0.5

表9 TSJA-30/0.5的混联模型中界面极化支路参数计算结果Tab.9 Calculation results of interface polarization branch parameters in hybrid model for TSJA-30/0.5

表10 TSJA-30/0.5的混联模型中R-C串联极化支路参数计算结果Tab.10 Calculation results of R-C series polarization branch parameters in hybrid model for TSJA-30/0.5

表11 TSJA-30/0.5的扩展Debye模型中Rg、Cg计算结果Tab.11 Calculation results of Rgand Cgin extended Debye model for TSJA-30/0.5

基于表8～12求取两模型的各参数吻合度，结果如表13所示。由表13可以看出，混联模型重构FDS曲线后的实测值与计算值吻合度均高于扩展Debye模型，其中扩展Debye模型的介质损耗因数和复电容实部的吻合度仅分别为0.660和0.801，平均吻合度也仅为0.803，且两个模型实测值与计算值的吻合度差距相较于2.1节中结果更加明显，这是因为TSJ-30/0.5为已退役的油纸绝缘设备，经过长时间外部水分的入侵其油纸绝缘系统受潮老化严重，内部产生多种具有不同介电常数的杂质，不同电介质之间形成的界面极化更加复杂，绝缘系统内的弛豫极化过程无法由扩展Debye模型简单的拓扑结构得到真实反映。

表12 TSJA-30/0.5的混联模型中R-C串联极化支路参数计算结果Tab.12 Calculation results of R-C series polarization branch parameters in extended Debye model for TSJA-30/0.5

表13 TSJA-30/0.5数据重构FDS曲线的吻合度对比Tab.13 Comparison of the consistency of FDS curves reconstructed from TSJA-30/0.5 data

为了更进一步凸显扩展Debye模型拓扑结构的不足，在5条极化支路总数的基础上逐渐增加支路数使得计算值曲线不断逼近测试曲线，当参数吻合度在一段区间基本保持不变时停止极化支路总数的增加，具体结果如图4所示。从图4可以看出，就参数平均吻合度而言，当扩展Debye模型的极化支路总数为6～8时，参数平均吻合度均低于0.9，在极化支路总数为9时达到最高，在极化支路总数为10～15时，参数平均吻合度在0.9以上；从图4还可以看出，当扩展Debye模型的极化支路总数超过8时，各频域介电量的吻合度在一个较高的值附近上下波动。

图4 扩展Debye模型不同极化支路总数的各参数吻合度Fig.4 The consistency of parameters of different polarization branches in extended Debye model

因此，为了有效地反映感应调压器TSJA-30/0.5内部油纸绝缘复杂的弛豫极化过程，扩展Debye模型至少需要9条极化支路总数，而混联模型只需5条即可达到这一目标，而且在9条极化支路总数的情况下需要辨识20个参数，混联模型只需辨识12个参数。混联模型可大幅提高模型参数的辨识速度，简化参数求解结果的复杂性，对现场变压器绝缘状态的快速、无损诊断具有重要意义。

综合2.1节及2.2节分析结果可知，考虑了油纸绝缘界面极化的混联模型能够很好地表达不同测试环境下油纸绝缘的介电响应信息，特别的，当油纸绝缘受潮老化严重时，混联模型相较于扩展De‐bye模型的优势将更加明显，因此混联模型在现场油纸绝缘设备的水分含量评估方面更具应用价值。

3 混联模型参数求取及分析

3.1 混联模型特征参数的提取

由前文分析可知，本文构建的频域混联模型为剖析FDS蕴含的油纸绝缘受潮状态信息提供了重要的模型基础。为进一步挖掘混联模型参数与绝缘纸含水率的潜在联系，现求取剩下3组不同含水率样品的混联模型参数，结果如表14所示。

基于表2～4及表14分析含水率对混联模型各参数的影响规律，与含水率具有明显数学关系的参数（记为X1、X2、X3、X4）分别如图 5(a)、(b)、(c)、(d)所示。更进一步分析，X1、X2、X3、X4一一对应于模型中的绝缘电阻Rg、R-C串联极化支路极化电阻最大值、界面极化支路极化电阻最大值、R-C串联极化支路极化电容最小值。各参数与油纸绝缘含水率的拟合曲线及数学关系分别如图5、表15所示。

表14 3组样品混联模型参数求取结果Tab.14 Calculation results of parameters in hybrid model for three samples

表15 敏感参数与含水率的数学关系Tab.15 Mathematical relationship between sensitive parameters and water content

图5 混联模型中敏感参数与样品含水率的拟合曲线Fig.5 Fitting curves between sensitive parameters in hybrid model and water content

3.2 特征参数有效性的验证

为验证本研究提出的混联模型特征参数及其拟合方程的有效性，采用与前文同等材料及相同制备方法另行制作两组含水率分别为2.5%及3.1%的样品，分别编号为1、2。两个样品的测试结果如图6所示，对应的混联模型特征参数及含水率（MC）评估结果如表16所示。从表16可以看到，由于两个样品的含水率比较高，各自的评估误差比较大，但仍十分接近真实值，初步验证了本文提出的混联模型特征参数的有效性。

表16 验证样品的特征参数及含水率评估结果Tab.16 The characteristic parameters of the samples for verification and the evaluation results of their water content

图6 验证样品的FDS实验测试数据Fig.6 FDS test data of the sample for verification

4 结论

以混联模型为研究对象，结合实验与油纸绝缘设备实测的FDS数据，研究了基于混联模型的油纸绝缘受潮状态评估方法，主要得到以下结论：

（1）在辨识混联模型拓扑结构中的各参数时，当极化支路总数为5～7时，参数辨识效果较好，因此对绝缘状态不同的油纸绝缘设备应按照5～7条的极化支路总数进行模型的参数辨识，且一般来说m应不小于M。

（2）混联模型的拓扑结构相较于扩展Debye模型在表达油纸绝缘系统受潮老化后的介电响应信息更加精确，特别是当油纸绝缘受潮老化严重时这一优势更加突出，扩展Debye模型需要多条极化支路（本研究至少9条）才能达到与混联模型相同的表达效果（5条极化支路）。

（3）提取了对油浸绝缘纸水分含量敏感的混联模型特征参数：绝缘电阻Rg、R-C串联极化支路极化电阻最大值、R-C串联极化支路极化电容最小值以及界面极化支路极化电阻最大值，并分别建立了上述参数与水分含量的定量关系式。

值得说明的是，本文提出的混联模型特征参数与绝缘纸含水率的估计关系式是基于未发生老化纸板的FDS测试数据得出的。为提高本文所提含水率评估方法的可靠性，还需进一步研究不同老化程度样品的FDS特性与含水率的关系，丰富绝缘纸的含水率评估方法。