交联聚乙烯绝缘电缆老化的介电响应与局部放电特性研究

丰利军，祝 曦，尹 毅，余林刚

（1.海军研究院，上海 200235；2.上海交通大学，上海 200240；3.南京工业大学，江苏 南京 211816）

0 引言

交联聚乙烯（XLPE）因其优异的绝缘性能而广泛用于电力系统的输配电电缆中[1]。但是电缆在长期运行过程中，电缆绝缘会受到电应力和热应力的影响，造成绝缘老化降解、电气绝缘性能下降[2-3]。随着电网电压等级的不断提高，电缆绝缘将承受更高的电场应力并面临更严苛的运行环境。因此，电缆绝缘的状态诊断和老化评估对电力系统的安全可靠运行具有重要意义。

针对长期服役条件下电缆绝缘材料的电气性能、理化特性以及机械结构等演变规律，国内外学者提出了多种检测分析方法以及表征老化特性的特征参数，如泄漏电流、介质损耗因数、电压耐受指数、羰基指数、断裂伸长率等[4-8]。尽管通过对上述特征参数的分析可间接获得材料化学成分和物理结构等信息，但基于实验测试的分析结果仍不能直接从分子或原子的微观角度来解释材料的降解与老化行为。因此，应用分子模拟方法来研究交联聚乙烯绝缘的老化特性，从而准确获取样品的微观参数，可以弥补常规测试无法直接获得材料微观特征参数的不足。

近些年，基于分子模拟方法的量子化学计算在聚合物绝缘中得到了广泛的应用[9]。T TAKADA等[10]通过量子化学仿真指出，聚乙烯绝缘中的化学缺陷会影响材料中陷阱能级的分布；WANG W等[11]研究发现聚乙烯分子链的交叉取向会产生电子陷阱，而分子链之间的相互作用是引入空穴陷阱的主要原因；ZHU X等[12]结合实验测试进一步探究了聚乙烯物理缺陷与化学缺陷的成因，并通过仿真获得了聚乙烯固有电气强度的绝对上限。但目前对不同老化状态下聚乙烯材料的量子化学计算与研究较少。而分析并构建老化聚乙烯分子链的仿真模型，开展相关的量子化学计算，对揭示电缆绝缘的降解行为与老化机理有重要意义。

本文以国产XLPE模型电缆为研究对象，对不同老化状态的模型电缆进行等温松弛电流与局部放电检测，并建立聚乙烯分子链的量子计算仿真模型，获得其在电场应力下的能级分布、电荷分布等微观参数，探究聚乙烯分子链微观变化对电缆绝缘介电性能的影响规律。

1 实验

1.1 实验对象及老化实验

以国产XLPE模型电缆为研究对象，其原料为超净低密度聚乙烯基础树脂，添加0.2%～0.3%硫代双酚类抗氧剂以及1.6%～1.8%过氧化二异丙苯交联剂。对模型电缆进行加速热老化实验，利用穿心变压器控制老化实验温度为135℃，使用橡塑海绵管对电缆进行保温，同时使用高压直流源对该模型电缆进行极化，控制其绝缘中的平均电场为15 kV/mm。分别取未老化电缆、老化第10天电缆与老化第30天电缆作为待测试样。

1.2 等温松弛电流（IRC）测试

将电缆两端外屏蔽层剥离，剥离长度为20 cm，用沾有无水乙醇的无纺布擦拭掉绝缘表面污垢。在测试前，短路电缆24 h以排除绝缘中的残余电荷。等温松弛电流三相同步测试系统如图1所示。电缆线芯与测试系统高压端相连，铜带屏蔽与测试系统的信号线相连。极化电压为700 V，极化时间和去极化时间都为1 800 s。

图1 等温松弛电流测试系统Fig.1 IRC measurement system

1.3 局部放电检测

局部放电检测回路如图2所示。无局放变压器输出工频交流高压，保护电阻为10 kΩ。测试回路中所有接线使用直径为28 mm的蛇皮管与直径为150 mm的均压环，耦合电容为1 000 pF。局放仪检测频带为10 kHz～1 MHz，测试现场背景噪声为0.04 V。待测电缆样品两端半导电剥离80 cm，剩余半导电接地，线芯一端通过均压环与高压相连，另一端浸入变压器油中以避免线芯放电。测试电压最大值分别为5 kV和9 kV，测试时间为1 800 s。

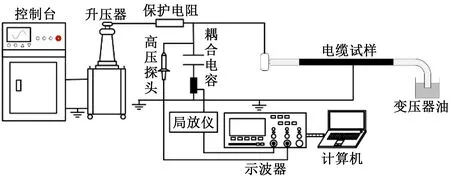
图2 局部放电检测系统Fig.2 Partial discharge measurement system

1.4 量子化学计算

为描述聚乙烯材料中微观粒子的运动状态，可采用量子化学计算方法。该方法可将电子的运动状态描述为波函数，使得对电子的求解转化为对电子波函数的求解。常用的量子化学计算方法有从头计算法、半经验法与密度泛函理论等[13-15]。本文使用Gaussian 09软件，采用半经验法PM6进行求解计算。构建3种聚乙烯分子模型，分别为聚合度为12的聚乙烯链（C24H50）、包含1个羟基的聚乙烯链（C23H47CH2OH）和包含1个羧基的聚乙烯链（C23H47COOH），相应地命名为P1、P2和P3，如图3所示。另外，沿x轴及聚乙烯主链方向上施加电场，场强由0.001 a.u.（1 a.u.=5.142×1011V/m）逐渐增大至0.004 a.u.，研究聚乙烯分子链在不同电场下的极化率、电荷分布等。需要说明的是，在量子化学计算中电场会直接作用在化学键上而改变分子系统的哈密顿量，进而改变分子能级分布。但这一过程不考虑载流子在电场作用下的热失控与自持加速行为，因此仿真中的电场强度会远大于聚乙烯材料的实际击穿场强。

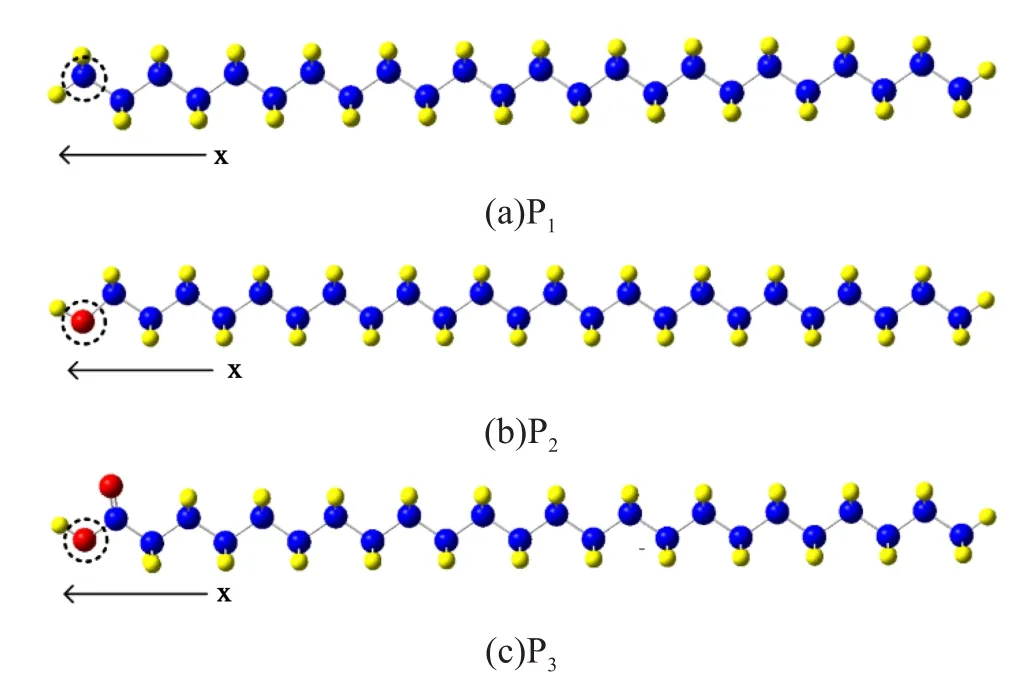
图3 具有不同官能团的聚乙烯长链Fig.3 Polyethylene chains with different functional groups

2 实验结果

2.1 等温松弛电流

根据J G SIMMOMS等[16]提出的等温松弛电流理论，聚合物中的陷阱呈非连续离散分布，其电子陷阱深度ΔE与时间t存在式（1）所示关系。

式（1）中：Ec为导带能级；Et为陷阱能级；k为玻尔兹曼常数；T为温度；v为逃逸频率。

去极化电流I(t)的表达式如式（2）所示。

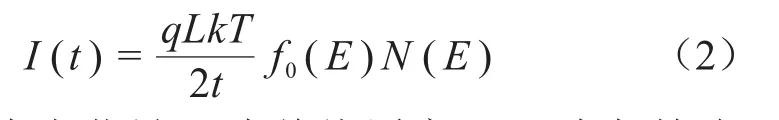
式（2）中：q为电荷量；L为绝缘厚度；f0(E)为起始陷阱能量密度；N(E)为陷阱密度。

从式（1）～（2）可以看出，t和ΔE呈正相关，I(t)·t与N(E)呈正相关。因此，利用I(t)·t-t曲线可有效地反映介质内部的陷阱分布。进一步，可利用三阶指数对去极化电流数据进行拟合，如式（3）所示。

式（3）中，αi和τi是与绝缘状态有关的量；I0为电缆松弛电流最终达到平衡时的稳态值。

最终得到I(t)·t-t的分峰曲线如图4所示。从图4可以看出，不同老化状态电缆的等温松弛电流分峰曲线出现了明显的差异。在未老化的电缆中，整体峰峰值出现在10 s附近，而随着老化程度的加深，整体峰向右移动。当老化30天后，整体峰峰值出现在100 s附近。根据式（1）中t与ΔE之间的关系，可以推测出材料中陷阱深度随老化时间的增加而变大。另外，在老化初期，分峰曲线中峰2和峰3的幅值差别较小，但随着老化程度的加深，二者之间的差异逐渐增大。尤其在老化30天后，代表老化新增缺陷的峰3占据了总体曲线的大部分，这说明老化电缆绝缘中的深陷阱密度大幅增加。

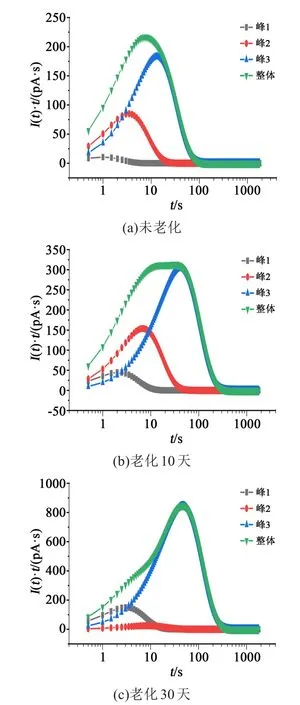
图4 不同老化状态电缆的等温松弛电流测试结果Fig.4 IRC test results of cables with different ageing states

基于等温松弛电流理论，给出老化因子A的计算方法，如式（4）所示[17]。

式（4）中：Q(τ3)代表因老化造成的界面极化决定量；Q(τ2)代表晶区与无定形区的界面极化决定量，一般认为Q(τ2)的变化不大，因此可作为计算老化因子A的基准，老化因子A越大，材料的老化程度越高。Q(t)的计算方法如式（5）所示。

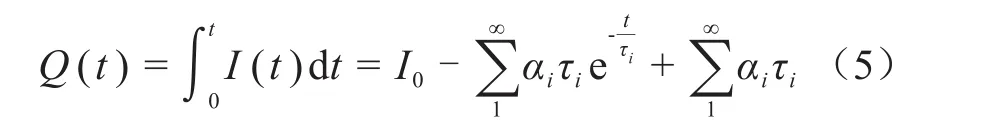
等温松弛电流的三阶指数拟合结果与计算得到的老化因子A如表1所示。从表1可以看到，随着老化时间的增加，反映电介质去极化过程的时间常数τ增大，老化因子A也增大。

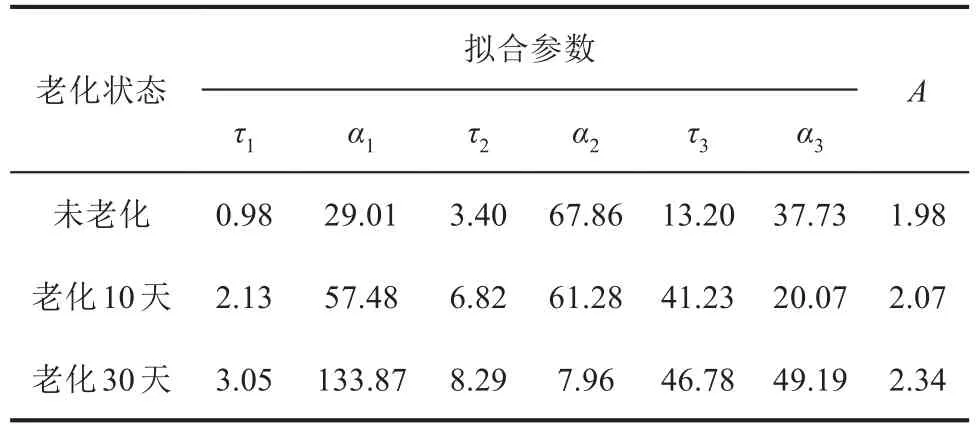
表1 电缆等温松弛电流的拟合结果Tab.1 Fitting results of IRC in cable samples

2.2 局部放电

电缆局部放电测试结果如图5所示，其中左侧图对应的施加电压为5 kV，右侧图对应的施加电压为9 kV。为直观地描述放电的密度分布，将放电-相位平面进行网格划分，统计落在各个网格中的放电次数，并利用网格中的最大放电次数对其他网格数据归一化，放电越密集则数值越接近1，网格颜色更接近红色。从图5可以看到，电缆样品的放电存在典型的相位分布特征，即电压正半周下的放电相位分布较宽，但放电幅值较小；而电压负半周下的放电相位分布较窄，但放电幅值较大。此外，随着老化时间的增加，放电强度显著增大。尤其在9 kV电压下，未老化电缆的放电幅值最小，最大放电量仅为2.2 V，而老化10天后电缆的最大放电量增至3 V，老化30天后达到4 V，且放电更为密集。

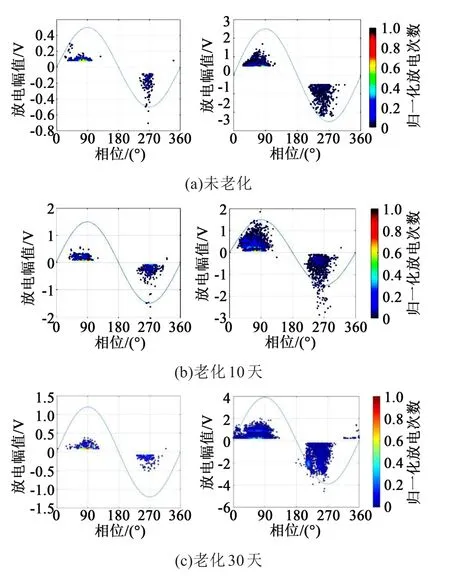
图5 不同老化状态电缆的局部放电测试结果Fig.5 Partial discharge test results of cables with different ageing states

对平均放电次数进行统计，结果如图6所示。从图6可以看出，随着老化程度的加深，电缆绝缘中的放电次数显著增加。在9 kV电压下，未老化电缆的平均放电次数为13 s-1，而老化10天和老化30天电缆的平均放电次数分别达到67 s-1和107 s-1。

图6 不同老化状态电缆的局部放电次数Fig.6 Partial discharge number of cables with different ageing states

2.3 量子化学计算

2.3.1 陷阱能级分布

3种聚乙烯链的能级分布结果如图7所示，其中前线轨道LUMO和HOMO分别代表导带的最低能级和价带的最高能级，即高于LUMO能级的能带上没有电子，而低于HOMO能级的能带上都被电子占据[18]。

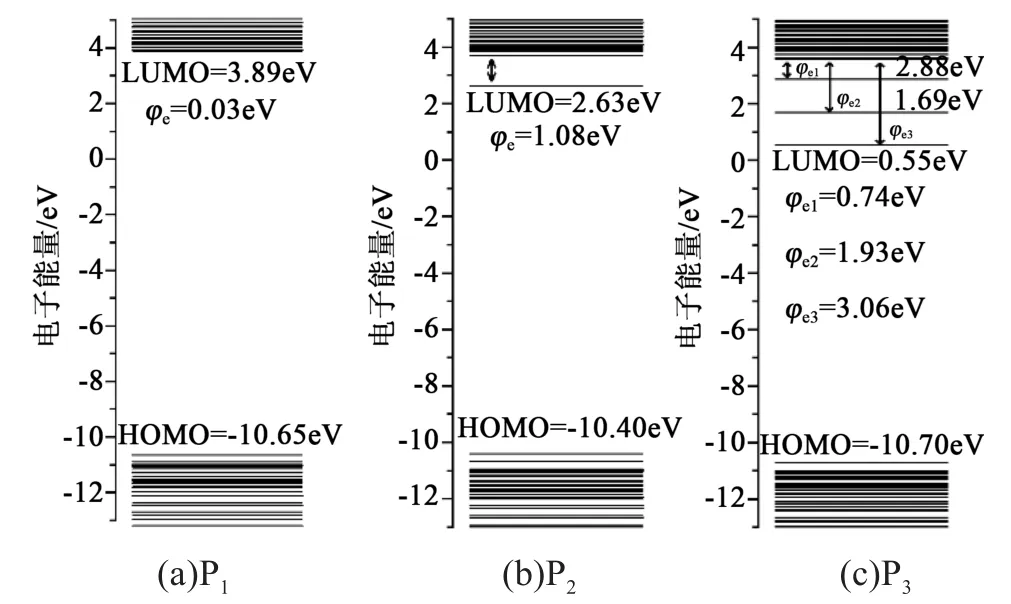
图7 聚乙烯分子链的能级分布Fig.7 Energy level distribution of polyethylene molecular chain

从图7可以看到，3种分子链的HOMO轨道能级差别不大，均在-10.65 eV左右，但LUMO轨道出现了明显的差异。P1的LUMO为3.89 eV，P2降至2.63 eV，而P3最小，仅为0.55 eV。LUMO轨道的不同造成了导带附近能级分布的变化，如P1中导带附近能级分布较为均匀，并未出现孤立能级；而P2中LUMO轨道孤立，与临近能级存在一定的距离；在P3中，除了LUMO，还存在两个孤立能级，分别为1.69 eV和2.88 eV。

根据聚乙烯分子链的能级分布，计算电子陷阱深度φe，φe定义为孤立能级与临近最近导带能级之差[19]。P1中几乎不存在陷阱，陷进深度仅为0.03 eV，P2中形成的陷阱深度为1.08 eV，其相比与P1有所增加。而在P3中，由于其能带中存在3个孤立能级，因此P3中形成3个陷阱，深度分别为0.74、1.93、3.06 eV。

2.3.2 电子云分布

设置等密度面数值为0.02，给出P1、P2和P3陷阱能级上的电子云分布，如图8所示。从图8可以看出，P1中的电子云在分子长链上均匀分布，P2中的电子云聚集在-OH附近，形成了聚乙烯分子链中典型的陷阱点；而在P3中的3个陷阱能级处，电子云均在-COOH附近聚集。表明聚乙烯链中碳氧官能团的出现会改变分子链的能级分布，从而引入陷阱能级。另外，随着基团成分与结构的变化，陷阱数量与深浅也会随之变化。

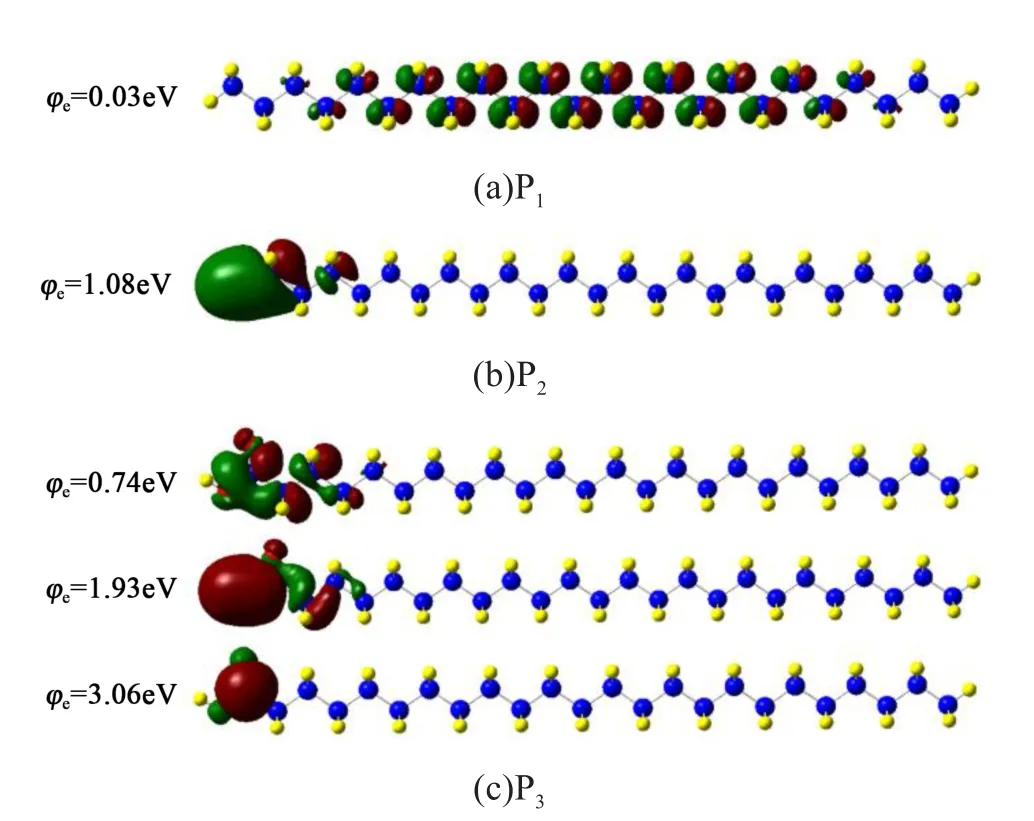
图8 聚乙烯分子链的电子云分布Fig.8 Electron cloud distribution of polyethylene molecular chain

2.3.3 能量变化

对3种聚乙烯分子链施加电场，获得不同电场下分子链的能量，结果如图9所示，其中1 hartree=4.359 7×10-18J。由于分子体系处于束缚态，原子间的相互作用能是负值，因此能量的数值为负数，即数值越小能量越大。为便于描述，后文中对能量数值的描述均使用取绝对值后的结果。

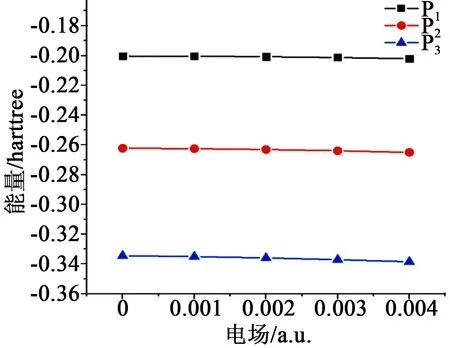
图9 不同电场下的分子链能量Fig.9 Molecular chain energy under different electric fields

从图9可以看出，对于同种聚乙烯分子链而言，分子能量（绝对值）随电场的增大而增大，这说明在电场作用下原子间的键能增大，分子中库仑势增大，造成了分子总能量的增大。通常，分子体系的稳定性与能量大小密切相关，体系越稳定则能量越小[20]。因此，随着电场的增大，聚乙烯链的分子稳定性降低。在相同的电场下，3种聚乙烯分子链的能量从小到大依次为 P1、P2、P3，可见P1分子链的稳定性最好，而碳氧官能团的引入会降低分子体系的稳定性，其中-COOH对分子稳定性的影响最大。

2.3.4 偶极矩与电荷

不同电场下聚乙烯分子链的偶极矩如图10所示。对于同一分子链而言，偶极矩会随电场的增大而增大。这是由于分子链内的电荷在电场作用下发生迁移，且随着电场的增大，更多的电荷会在分子链的端部聚集，从而造成偶极矩增大。

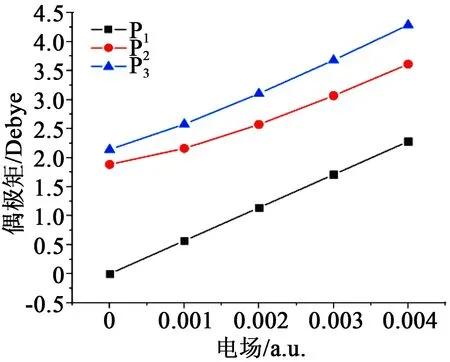
图10 聚乙烯分子链在不同电场下的偶极矩Fig.10 Dipole moment of polyethylene molecular chain under different electric fields

从图10可以看出，当电场强度为0时，P1的偶极矩为0，而P2、P3的偶极矩分别为1.88 Debye和2.14 Debye，可见碳氧基团的引入使非极性的聚乙烯分子变成了极性分子。在相同的电场下，3种聚乙烯分子链的偶极矩从小到大依次为P1、P2、P3，说明-COOH的引入使聚乙烯分子链在电场作用下的极化效果更明显。

同时，分析电场作用下聚乙烯分子链左侧端部非氢原子（图3中虚线圈出的原子）负电荷量的变化情况。考虑到3种聚乙烯分子链的结构不同且不同原子的电负性也不同，直接对比原子电荷量的高低是没有意义的。因此，这里以电场为0时该原子的电荷量为参照，计算不同电场下电荷量的变化值，结果如图11所示。从图11可以看出，随着电场的增大，P1中碳原子的电荷量变化极小，而P2、P3中氧原子电荷量的变化量显著增加。可见，对于不存在缺陷的聚乙烯分子链P1，其在电场作用下的电荷增减量较小；而对于存在碳氧基团的分子链，由于其自身所存在的电子陷阱，使电荷更容易入陷，从而造成端部原子电荷量增加。

图11 不同电场下的电荷量变化量Fig.11 Variation of charge under different electric fields

3 讨论

从等温松弛电流与局部放电实验结果可以看到，伴随着电缆老化的加深，聚乙烯绝缘的介电响应会发生变化，具体表现在等温松弛电流时间常数变大、陷阱密度与深度增大、局部放电强度增大。通过对绝缘材料的宏观电气性能分析、微观理化性能检测，可揭示聚乙烯绝缘的老化降解机理。本研究基于量子化学仿真结果，从分子与原子尺度对聚乙烯绝缘因老化所产生的介电性能变化进行探究。

首先，对聚乙烯分子链的热氧老化过程进行分析，化学反应过程如图12所示。烷烃在热氧作用下被氧化，聚乙烯长链中可能会引入氧原子，形成饱和基团羟基（-OH）或不饱和基团醛基（-CHO），且这两种中间态分子可相互转换。随着热氧老化进一步推进，中间态分子可能会进一步被氧化，形成羧基（-COOH）。因此，本研究所构建的P1、P2与P3分子链可近似模拟聚乙烯老化发展的3个阶段。

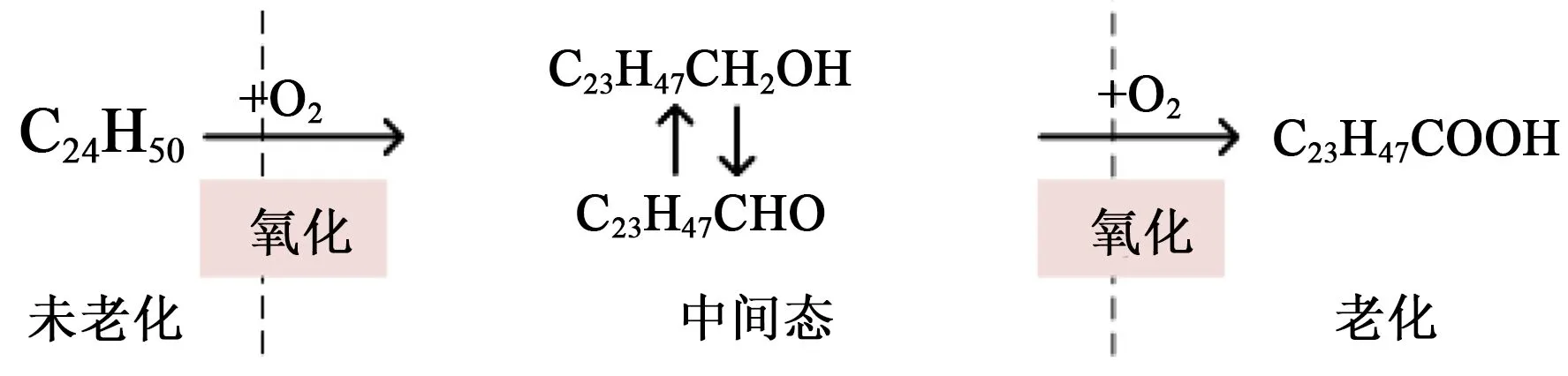
图12 聚乙烯分子链的氧化过程Fig.12 Oxidation process of polyethylene molecular chain

从量子化学仿真中可以看到，未老化的P1分子中能级分布均匀，而老化的P2分子中出现1个孤立能级，陷阱深度达1.08 eV；随着老化加剧，在P3分子中陷阱数量不但增加到3个，而且陷阱深度也增大到3.06 eV。这是由于羟基与羧基基团的引入使聚乙烯分子链中出现化学陷阱，且陷阱的数量与缺陷分子的结构密切相关。以羧基（-COOH）为例，提高等密度面数值为0.05以显示主要电荷分布，如图13所示。可以看到羧基中的C=O构成了最深的陷阱，而C-O形成了1.93 eV的次深陷阱。另外，由于羧基基团对聚乙烯分子链整体结构的影响，形成了结构型浅陷阱，陷阱深度为0.74 eV。因此，在电缆的老化过程中，聚乙烯绝缘不断氧化降解，形成数量更多、成分更为复杂的官能团，从而造成陷阱数量与陷阱深度的增加，这一过程也与等温松弛电流的测试结果一致。

图13 羧基附近电子云分布Fig.13 Electron cloud distribution near carboxyl group

同时，在电场作用下，未老化的P1分子表现出最低的分子能量、最小的偶极矩以及最小的电荷增量。随着老化的加深，聚乙烯分子链的稳定性进一步降低，极化率与电荷转移显著提高。因此，在进行局部放电测试时，老化的电缆绝缘材料有更大的极化强度，极化所产生的电荷更多，材料内数量更多且能级更深的陷阱会使电荷入陷，从而造成局部电场集中，最终造成更强的局部放电。

4 结论

（1）随老化程度的加深，材料中陷阱密度与深度增大，这与热氧作用下聚乙烯分子链中出现的碳氧基团有关。同时，碳氧官能团的种类会直接影响聚乙烯分子链的陷阱能级分布。在老化前期，分子链中出现的羟基会引入1个能级陷阱（1.08 eV），而进一步老化形成的羧基会产生3个能级陷阱（0.74、1.93、3.06 eV），从而造成老化的电缆绝缘中陷阱数量与深度的增加。

（2）相比于纯聚乙烯分子链，含碳氧基团聚乙烯分子链在电场作用下的稳定性更差、偶极矩更大、分子链内电荷转移更明显，电荷也更易被陷阱俘获。当官能团由羟基变为羧基时，聚乙烯分子链的稳定性进一步降低，使电缆绝缘中空间电荷更易于聚集，从而造成电场集中，提升了老化电缆中局部放电的强度。