单点混合磁悬浮系统的自抗扰控制仿真研究

苏芷玄，杨杰，彭月，彭飞

(1.江西理工大学 永磁磁浮技术与轨道交通研究院，江西 赣州 341000；2.江西省磁悬浮技术重点实验室，江西 赣州 341000；3.北京电子科技职业学院 汽车工程学院，北京 100176)

磁悬浮列车具有非接触、少磨损、低噪音、更智能等优势，是发展下一代地面交通工具的首选制式。自上世纪80年代以来国内开始对磁悬浮运行技术进行研究，经过科研院所近40年的努力，2016年长沙磁浮快线正式通车运营。2019年5月我国时速600 km/h的高速磁浮实验样车在青岛下线，并于2020年6月在上海同济大学磁浮试验线顺利试跑。这标志着我国在磁悬浮轨道交通领域实现了技术突破，也意味着新的磁浮交通发展阶段的开启。在混合悬浮技术发展的数十载里，国内外学者先后提出并发展了多种混合悬浮模式，例如：电磁永磁混合悬浮[1]、高温超导与永磁结构的钉扎悬浮[2]、超声悬浮−气浮混合式[3]等。对于单自由度混合悬浮结构的研究，郭建光[4]提出一种悬浮球在上、磁−电结构在下的磁斥型单点混合悬浮结构；马凤莲等[5]提出将永磁体置于悬浮球内部，将主动反馈控制与具有出色负载优势的永磁体技术结合，取长补短，由此充分发挥磁悬浮技术的性能优势。然而，由于混合悬浮系统本质是一个不稳定的非线性系统，且在实际悬浮环境中受风力、传感器温漂等外界因素均有可能导致车辆悬浮环境的变化[6]，因此，在仿真试验平台设计和工程实现中，采用较强抗扰动能力、鲁棒性以及不依赖于被控对象精确模型等优势的控制算法显得尤为重要。目前，在磁悬浮系统的控制方法中，逐步形成了多种控制策略，例如，经典PID控制器[7]、神经网络控制[8]、滑模变结构控制[9]等。其中，基于反馈控制框架下的自抗扰算法(ADRC)[10-11]不完全依赖于精准数学模型，且具有响应快速性与较强的抗扰动能力等优点，可逐步探索性向磁悬浮控制领域发展，如此为本文的课题研究提供借鉴与参考。本文以“红轨”系统[12-13]为研究基础，现有悬浮列车采用多组悬浮架，面临点与点之间耦合的复杂环境，现有研究往往通过机械防滚梁结构解耦以及电气解耦等方式[14-15]将其间接转化为独立悬浮系统控制问题。单点混合悬浮系统作为多点悬浮的一个基本单元，对于其模型的研究可作为混合悬浮列车应用的理论基础，研究其控制性能与抗扰动能力对于混合悬浮列车运行安全具有一定意义。由于永磁材料存在非线性磁力与不可控特性[16]等问题，因而混合悬浮车辆面临着如何实现电磁控制的难点。本文将基于Levant微分器的自抗扰控制算法引入到单点混合悬浮球系统中，也为未来实现“永磁材料为基础，电磁控制为手段”的工程实践提供了一定的理论论证。

1 单点混合悬浮系统数学模型

本文以单点悬浮球系统[17]为基础，在小球上端加入一个永磁体，通过永磁体所产生的吸力克服小球自身重力，而电磁力作为稳定性调节作用。本文采用垂向串联式混合悬浮结构，为研究方便，在不影响仿真结果的前提下，作如下假设：

1)磁路中铁磁材料的磁导率无穷大并且磁势均匀地分布于气隙和永磁体上；

2)忽略绕组和永磁体的漏磁通。

混合悬浮球系统参数如下：电磁铁线圈匝数为N，悬浮间隙为x，线圈的电压为u(t)，电流为i(t)，永磁体磁化方向向上、厚度为hmp，半径为r mp，永磁体矫顽力为Hc，磁导率为μr，铁球质量为m，重力加速度为g，永磁体截面积与铁芯截面积均为S，悬浮状态受力分析如图2所示。Rmp为永磁体的磁阻，Rc为气隙的磁阻，Rl为铁芯磁阻，在上述假设下，混合磁铁的等效磁路模型如图3所示。

图2 单点混合悬浮球系统模型Fig.2 Single point hybrid suspension ball system

图3 单点混合磁铁等效磁路模型Fig.3 Equivalent magnetic circuit model of single point hybrid suspension ball system

由于铁芯的磁阻远小于空气磁阻与永磁铁磁阻，可忽略不计，因而磁路总磁阻如式(1)所示，其中，μ0为空气的磁导率，永磁体相对磁导率μr=μmp/μ0。

由磁路定律计算磁路磁通可得式(2)：

磁铁绕组在气隙x(t)处的线圈电感L与气隙磁密B如式(3)所示：

则在t时刻的电磁力如式(4)所示：

由式(4)可以看出，混合悬浮系统的电磁力与纯电磁悬浮的电磁力不同，在加入了永磁体后，混合悬浮系统的电磁力与电流、气隙的平方不再呈线性关系。

混合悬浮球在垂直方向的力学方程如式(5)所示。其中，fd(t)为外界扰动量。

综上所述，系统的动态模型总结如下：

单点混合悬浮球在平衡点处的边界条件如式(8)所示：

利用泰勒级数将方程(7)在平衡点处线性化，可得到一个近似的线性化模型，忽略高阶项可得到如下线性方程组，如式(9)所示：

其中：

以电压为输入变量，(Δx,̇,Δi)T作为状态变量，那么可以得到状态方程为式(10)：

忽略扰动量的影响后，由状态空间方程可以得到系统的特征方程，如式(11)所示：

由劳斯判据可知，若劳斯表第1列出现负值，则该系统为不稳定系统。由于式(11)特征方程中s0的系数为负，因而该系统是一个不稳定的系统，因此需要增加一个控制器来保证系统的稳定悬浮。

现选取系统状态变量x1=x(t),x2=ẋ(t)，取控制输入为u=u(t)，f(x1,x2)为内扰作用，w(t)为外扰作用，由此可将单点混合悬浮球系统近似成一个2阶系统。将表1参数代入混合悬浮球系统状态方程(10)，可得实参化模型如式(12)所示：

表1 控制对象参数Table 1 Parameters of the controlled object

2 自抗扰控制器的设计

结合上一小节的理论分析，本节将根据欠稳定系统进行控制算法设计。通过利用系统输出反馈信息对混合悬浮系统施加主动调控的控制策略，分别设计传统PID与自抗扰控制算法，并在此基础上进行抗扰动等方面性能的分析与对比。

传统的PID控制算法简单、可靠性较高，通过利用误差信号的比例、积分、微分的线性组合而成的控制量，进而对被控对象进行控制，控制原理框图如图4所示。然而在实际的工业控制过程中往往存在非线性以及时变不确定性等问题，进而难以建立完全精确的数学模型。

图4 PID控制系统原理框图Fig.4 Structure diagram of PID controller

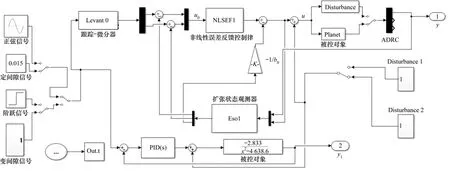
由跟踪−微分器(TD)、扩张状态观测器(ESO)以及非线性状态误差反馈控制律(NLSEF)组成的自抗扰控制器，通过跟踪−微分器安排过渡过程以解决快速性与超调量的矛盾；以扩张状态观测器为手段对总扰动实时估计并消除，进而将复杂的非线性被控对象转化为简单的积分串联型，且不完全依赖于精确的数学模型，其基本结构如图5所示。

图5 自抗扰控制器结构Fig.5 Structure of active disturbance rejection controller

2.1 跟踪-微分器的设计

Levant微分器[18-22]能够保证在随机噪声环境中的信号跟踪与微分求取能力都较好的前提下，还对信号的测量误差具有鲁棒性，以及具有控制参数相对较少、结构简单的优点。因此，本文采用Levant微分器作为跟踪-微分器及安排过渡过程的环节。Levant微分器表达式如(13)所示，其中，C是输入信号v(t)导数的拉普拉斯常数上界，且满足α>C>0，λ2>4C(α+C)/(α-C)。

Levant微分器中υ实现对v(t)的跟踪，u1则实现对微分信号dv(t)/dt的跟踪。

为验证Levant微分器性能，设定输入为带有噪声的正弦信号sin(2πt)，在MATLAB/SIMU‐LINK仿真平台分别验证其信号跟踪性能与微分获取性能，仿真结果如图6～7所示。

图6 Levant微分器信号跟踪Fig.6 Signal tracking by Levant differentiator

由仿真结果知，图6上图中的噪声信号已完全把理想正弦信号掩盖，下图的Levant微分器较好地跟踪上理想正弦信号，对比可得Levant微分器的跟踪性能和降噪性能都比较好。图7上图为差分法求得导数信号与理想导数信号，下图为Levant微分器估取的导数信号，由于噪声毛刺的存在差分法无法很好的获取理想导数信号，对比可得Le‐vant微分器具有较好的微分估计性能。

图7 Levant微分器微分信号获取Fig.7 Differential signal acquisition by Levant differentiator

2.2 扩张状态观测器的设计

对于一个受到外界干扰的2阶对象：

式中：f(x1,x2,t)为内扰作用，w(t)为外扰作用，b为对象已知参数，u(t)为控制输入。将控制过程中的包括外扰与内扰在内的所有扰动作用量当作一个新的未知的状态变量x3(t)加入原系统中，如式(14)所示，即在原系统的基础上扩张出一个新的状态，此时原系统方程如式(15)所示：

由于单点混合悬浮球系统是一个2阶对象，所以对其设计一个3阶的扩张状态观测器，观测器表达式如式(16)所示：

其中，fal函数表达式如(17)所示：

这样，在参数b已知或者接近的情况下，就能使扩张观测器的状态变量z3(t)跟踪系统的状态变量x3(t)，且有较大的适应范围。z1,z2,z3为悬浮间隙的估计值、输出悬浮间隙的微分以及单点混合悬浮系统的扩张状态观测量，分别跟踪x1,x2,x3。

x3为单点混合悬浮系统的扩张状态即系统总扰动，结合式(12)将总扰动的作用扩张为一个新的未知的状态变量如式(18)所示：

其中：-10.09ẋ1-4 638.6x1为系统内扰；fd为系统外扰。

2.3 非线性状态误差反馈控制律的设计

本文采用fal函数构造非线性组合，表达式如式(19)所示：

其中：e1为预设悬浮间隙与实际悬浮间隙之差；e2为微分器输出的悬浮间隙微分信号与扩张状态观测器输出的悬浮间隙微分信号之差。fal函数表达式同式(17)，且满足0

通过将实参化模型式(12)转化为式(20)形式的串联标准型，简化控制系统，化繁为简。

单点混合系统的控制量u为：

式中：b=-2.833为单点混合悬浮系统实参化模型式(12)中控制量u的系数，是对总扰动分量的补偿，是用非线性反馈去控制积分串联型的分量。

3 仿真实验

为了与ADRC的仿真控制效果进行对比，本文还设计了PID控制器，选取仿真结果较好时的参数为：Kp=-5 000,Ki=-37 640,Kd=-60。

单点混合悬浮球系统的控制算法参照上节所设计的基于Levant微分器的非线性自抗扰控制器，按照图5所示的非线性自抗扰控制器结构框图进行设计，非线性自抗扰控制器参数设定如表2所示，通过MATLAB/SIMULINK仿真平台搭建仿真模型如图8所示，设定初始悬浮间隙x为15 mm开展仿真实验。

图8 单点混合悬浮系统的ADRC与PID的仿真模型Fig.8 Simulation model of ADRCand PID algorithm for single point hybrid suspension system

表2 自抗扰控制器参数Table 2 Parameters of active disturbance rejection controller

为了验证自抗扰控制器的性能优越性，仿真设计方案如下：1)阶跃响应实验：无扰动状态下，将ADRC算法与PID算法的阶跃信号跟踪情况进行对比；2)冗余性实验：在0.7 s和1.3 s时刻，同时突加一个5 N和50 N的外界扰动，比较2种算法的抗扰动能力；3)适应性实验：给定变化范围为12 mm与15 mm的方波间隙信号，对比观察2种算法的跟踪性能。4)鲁棒性实验：改变模型参数b，将参数b=−2.5，b=−1.5，b=−0.7代入仿真模型，得到悬浮高度响应曲线。

1)阶跃响应实验

在simulink仿真环境下，初始时预设15 mm的悬浮间隙，观察PID与ADRC的响应情况，仿真结果如图9所示。

由图9可以看出，给定间隙情况下ADRC与PID都可以在短时间内达到稳定，ADRC可在0.1 s内跟上响应并恢复稳定且最大间隙变化量仅为0.02 mm，而此时PID正处于给定悬浮间隙1.86倍的间隙变化中。由此可得ADRC有效地处理了快速性和超调量的矛盾。

图9 ADRC与PID定间隙的阶跃响应对比Fig.9 Step response comparison of the setting suspension gap between ADRCand PID

2)冗余性实验

在0.7 s与1.3 s时刻同时给2个控制器突加5 N与50 N的阶跃干扰，观察其冗余能力，仿真结果如图10所示。

图1 江西理工大学自主研发的永磁悬浮轨道交通系统“红轨”Fig.1“Red Rail”permanent magnet suspension rail transit system developed by Jiangxiuniversity of science and technology

图10 ADRC与PID突加阶跃负载时的冗余响应对比Fig.10 Suspension gap response of ADRC and PID

由图8可以看出，0.7 s突加5 N的阶跃干扰后，ADRC与PID控制均能重新达到悬浮状态，此时ADRC的最大间隙变化量只有0.3 mm，而PID的最大间隙变化量为1.3 mm，为ADRC的4.3倍，并且恢复稳定的时间也较ADRC而言缓慢了近4倍。当干扰量增大10倍时，可以明显看出ADRC稳定性能较强，其最大间隙变化量约为2.5 mm，远小于此时PID控制器的间隙变化量13.8 mm。由于ADRC中的扩张状态观测器可通过补偿扰动的方式将内扰与外扰进行估计与消除，因此ADRC比PID更能适应大范围负载的变化。由此可以得出结论：若存在悬浮列车中电磁铁或相邻控制点出现故障等问题时，ADRC具有更强的冗余能力和抗扰动能力。

3)适应性实验

结合“红轨”系统悬浮列车，考虑到Halbach阵列在拼接的轨道接口等处存在永磁材料，因此轨道面无法做到完全平整，如此极可能导致列车运行时出现悬浮间隙小范围波动的情况，因而研究PID算法与ADRC算法在悬浮间隙发生变化时对悬浮状态的跟随效果很有必要。通过改变预设的悬浮间隙，观察其适应与跟随间隙能力，具体设置如下：初始时刻设定悬浮间隙为12 mm，在0.6 s和1.2 s时刻分别将悬浮间隙提高3 mm，持续时间约0.3 s，仿真结果如图11所示。

图11 设定变间隙的ADRC与PID跟随响应对比Fig.11 Following response of ADRCand PID with changing suspension gap

从仿真结果可以得到，在初始时刻PID控制悬浮高度响应存在较大的超调，超调输出约为7.6 mm，而ADRC在初始时刻的超调输出仅约为0.6 mm。在设定方波信号的每一次间隙变化跳跃时刻PID控制和ADRC均存在超调，但是ADRC仅存在0.3 mm的微弱超调，而PID控制的超调量比ADRC高出约10.7%，这意味着ADRC在瞬时信号的跳变情况下，具备良好的适应性与跟随性，优于PID控制。

4)鲁棒性实验

在实际工程应用中，由于设备老化、工作环境变化等原因容易导致系统模型参数发生变化，而系统模型参数主要包括内外扰动系数、状态变量系数以及参数b。因为前2类系数变化都可被扩张状态观测器视为总扰动进行估计与消除，而参数b的变化会造成依据原系统参数设计的控制器的控制性能变差，所以研究参数b变化时自抗扰控制器的鲁棒性对于工程实现的具体应用有一定意义。

单点混合悬浮系统模型参数b=−2.833，现改变模型参数b，将参数b=−2.5，b=−1.5，b=−0.7分别代入模型，得到仿真结果如图12所示，可得结论如下：1)在模型参数b发生变化时，自抗扰控制器比PID控制表现出更强的鲁棒性。2)模型参数b在一定范围内改变时，ADRC基本可以保证铁球的稳定悬浮，但是随着其取值逐渐偏离原模型参数b，鲁棒性会随之减弱，抗扰动性能变差，但仍然能在0.2 s内恢复稳定，且超调量不超过1 mm。

图12 参数b分别为−2.5，−1.5，−0.7时悬浮高度响应曲线Fig.12 Response curves of suspension height when b is−2.5，−1.5，−0.7

4 结论

1)在给定间隙响应方面，ADRC相比PID响应速度提升了近4倍、超调量降低约43%。

2)在外加阶跃干扰量时，ADRC的悬浮间隙波动量为PID的0.23倍，且负载量越大ADRC适应性越强。

3)当模型参数b减小时，ADRC较PID而言仍能展示出较好的鲁棒性能。

基于Levant微分器的自抗扰算法的引入保证了跟踪效果以及抑制噪声能力的同时还降低了调参难度，提高了混合磁悬浮系统的控制性能。仿真表明，该算法具备快速性、稳定性、冗余性以及鲁棒性等优势，由此可对自抗扰算法用于控制混合悬浮系统的实际工程应用提供一定参考意义。就仿真结果中出现的轻微抖振现象，下一步可在跟踪微分器的基础上对自抗扰控制算法进行改进，如在设计跟踪微分器时采用在开关曲线附近引进线性区域或者使用光滑函数处理线性区域与非线性区域的切换等方法，进一步提高微分跟踪器的性能，由此可更加优化混合悬浮系统的控制性能。