抚仙湖历史水位反演与未来30年水位变化预测*
李加龙,李慧赟,罗潋葱,龚发露,张如枫,刘凤龙,吴松涛,罗碧瑜
(1:云南大学国际河流与生态安全研究院,昆明 650500) (2:中国科学院南京地理与湖泊研究所,南京 210008) (3:云南大学生态与环境学院高原湖泊生态与治理研究院,昆明 650500) (4:湖南人文科技学院,娄底 417000) (5:浙江省浦江县气象局,金华 321000) (6:广东省梅州市气象局,梅州 514021)
水位作为湖泊水情变化最直接和最重要的指标,在现代湖泊研究中具有重要意义. 水位波动不仅会直接引起水质的变化[1],还会通过影响水体中悬浮物浓度、透明度、溶解氧等指标进而影响水生植被[2];湖泊水位的持续上升会改变湖区原有的生态结构以及湖泊上下游的水文情势,当水位超过控制水位时还会引发洪水灾害[3];水位的持续下降会给生态环境安全带来严重威胁,并影响流域内水资源的利用[4]. 抚仙湖作为我国最大的深水型淡水湖,也是珠江源头的第一大湖,在水资源供给、防洪调控和生物多样性保护等方面发挥着重要作用[5]. 近年来,受气候变化和人类活动的共同影响,抚仙湖水位波动显著,尤其在遭遇2009-2010年百年一遇的极端干旱事件后,其水位于2014年降至历史最低(1720.87 m),给流域内居民生活用水和工农业用水带来严重影响,并危及湖泊生态系统健康. 因此,在极端气候事件频发和人类活动加剧的背景下,研究湖泊未来水位变化趋势,寻求有效的湖泊水位模拟方法,无论对湖泊生态系统健康稳定维持,还是对湖泊水环境保护和水资源合理利用,均至关重要.
近年来,已有诸多学者在湖泊水位模拟和预测方面展开了详细的调查和研究[6-7],取得了很好的成效. 例如,李云良等[8]基于BP神经网络对鄱阳湖水位进行模拟,结果表明神经网络模型可很好地反映鄱阳湖水位变化情况;万中英等[9]通过逐步回归法成功建立了鄱阳湖水位预测模型,实现了对鄱阳湖水位的短期精准预测. 上述方法虽然模拟效果较好,但需要大量数据对模型进行训练,且湖泊水位、水量变化属于物理过程,而上述方法的物理基础相对较弱,很难达到对未来湖泊水位进行有效预测的目的. 随着研究方法的深入,湖泊水动力模型因其完善的物理机制和对水动力学过程的全面考虑可实现对水位的精准模拟,深受广大学者欢迎. 目前广泛应用的湖泊水动力模型有EFDC[10-11]、MIKE系列(MIKE3、MIKE11和MIKE21)[12-14]、Delft3D[15-16]等,上述模型均可实现对湖泊水动力过程和水质的精确模拟. 本文选用的DYRESM水动力模型,与上述模型相比,具有代码开源且输入参数相对简单的优点,被国内外学者广泛应用于模拟不同类型的湖泊水动力和水质情况,并用来评估和预测未来气候变化对湖泊热力学及水质的影响[17-19].
抚仙湖属断陷型深水湖泊,其水位不仅受降水和地表径流影响,还受人类活动用水、水表面蒸发和河道出湖[20-21]以及地下水补给的影响. 张月霞等[22]利用IWIND-LR模型对抚仙湖水位进行了为期一年的模拟和验证,结果表明模拟水位与实测水位误差较小,但该模型在模拟过程中,未考虑河道出湖水量和人类活动用水对抚仙湖水位的影响. 实际上,历史上抚仙湖和星云湖通过隔河相互连通而具有一定的水量交换[23]. 此外,出流改道工程[24]以及工农业和居民生活用水均对抚仙湖的水位变化具有不可忽略的影响. 由于抚仙湖集水域尚无长时间序列的历史水文监测数据,故在无实测入湖水量的条件下,通过调节DYRESM水动力模型物理参数,并利用水量补偿法对2011-2017年入湖水量(地表径流和地下水量总量)进行反推,通过上述方法得到的2011-2017年逐月入湖水量与实测逐月降水量进行拟合,建立降水-入湖水量回归方程,便于在入湖水量缺测的情况下根据降水量计算入湖水量. 通过2007年抚仙湖实测入湖水量数据和1959-2010年长达52年的水位模拟结果,分别对回归方程准确性和DYRESM模型的精度进行验证. 为明晰未来气候变化对抚仙湖水位水量的影响,利用CMIP6(Coupled Model Intercomparison Project Phase 6)[25]中BCC-CSM2-MR模式下SSP245和SSP585两种情景中预测的未来气候状况,对抚仙湖2021-2050年水位变化趋势进行了预估,以期为应对气候变化情况下水资源合理调度提供科学依据和决策支持,也为其他类似的研究提供参考方法.
1 研究区概况
抚仙湖地处云南省玉溪市,位于昆明市东南部[26],距昆明市区约60 km,跨澄江、华宁和江川三县,为我国蓄水量最大的湖泊,隶属于南盘江水系,与星云湖通过隔河相连[27](图1). 其流域面积为674.69 km2,当湖面高程为1722.5 m时,水域面积约为216.6 km2,湖容量约为2.06×1010m3,约为滇池水量的12倍之多,占云南省湖泊总蓄水量的78%. 抚仙湖最大水深为158.9 m[28],位于北部,岸线长度为100.8 km,呈南北长条形,南北最大长度为31.4 km,东西最宽处位于北部(11.8 km),最窄处位于南部(3.4 km). 抚仙湖流域涉及8个镇,238个自然村,流域内总人口17.88万人[29]. 流域内农业、工业和城镇居民年均用水量分别约为3.8×106、3×106和2.6×106m3[30].
抚仙湖地处亚热带季风气候区,常年平均气温15.6℃,年内平均最高和最低气温分别为22.7和9.8℃;年均降水量为800~1100 mm,蒸发量在1200~1900 mm之间,年日照时数达2153 h,日照率为50%,全年无霜期近300 d[31-32]. 雨季分明,汛期为5-10月,汛期降水量占全年降水量的80%~90%[33]. 全湖无大河注入,主要靠降水和周围山间小溪汇集补给. 流域内有大小河流103条,其中主要河流35条. 入湖河流大多较短且具有间歇性特征,即水流大小依降水而定,旱季断流[34]. 天然出口河为海口河(图1),多年平均出流量为9.02×107m3[35]. 自2007年12月抚仙湖-星云湖出流改道工程建成运行后,改变了两湖间的千古流向,隔河也成为抚仙湖的出口河,平均每年有4.98×107m3水量注入星云湖,而海口河仅在特殊年份行使泄洪功能[23]. 经2020年8月-2021年8月逐月环抚仙湖考察,目前抚仙湖出湖闸门(海口河与隔河)均已关闭.

图1 抚仙湖地理位置、水深分布和主要出入流河道Fig.1 Location, water depth and main tributaries of Lake Fuxian
2 方法与数据来源
2.1 DYRESM模型
本文中使用的水动力模型为DYRESM(dynamic reservoir simulation model)[36-37]. 该模型最初由西澳大利亚大学水研究中心研发,为面向湖泊和水库的一维水动力模型,可以用来预测水温和盐度在垂直深度上的变化情况. DYRESM模型可单独运行进行水温和盐度的模拟,亦可与生态模型CAEDYM(computational aquatic ecosystem dynamic model)进行耦合,用来模拟水质和浮游植物、浮游动物、鱼类、底栖动物等生物有机体的生命过程[38],也可模拟水体和沉积物之间的营养盐交换,已在诸多水体中进行了成功应用. 例如,陆顶盘等[39]利用DYRESM对红枫水库水体热分层特征进行了模拟;Saddek等[40]利用DYRESM-CAEDYM模拟了萨瓦河水库水体的热分层结构和沉积物内源磷的释放;崔杨等[41]运用DYRESM-CAEDYM对中国沙河水库外源营养盐减少的潜在影响进行了模拟.
2.2 模型边界条件及参数设定
DYRESM模型需要的基础数据为水域地形信息(即各深度上的水面面积),和出流入流河道的数量以及各河口高程;边界条件包括气象信息和出入流流量与水质;初始条件即为模拟起始时刻的水温或者水质在垂直方向上的分布信息. 所需输入的气象信息包括太阳辐射(W/m2)、气温(℃)、水汽压(hPa)、平均风速(m/s)、云量(0~1)或太阳长波辐射(W/m2)、降雨量(m)和降雪(m,无降雪区域设为0)7个气象指标. 水域地形信息由抚仙湖湖底高程-面积关系生成,将抚仙湖以0.1 m水深进行分层,最大水深为158.9 m,分别计算各深度上的水面面积. 入流文件由抚仙湖9条省控入湖河流的逐日流量、水温及水质数据组成,由于仅考虑水位变化,故入湖河流水质浓度均设为0;出流文件由海口河、隔河两条出湖河道水量(两条河道根据各自运行时间进行处理)和人类活动用水量组成. 初始剖面文件中,在模拟不同时段水位时,只需调整文件中的初始水位数据即可. 模型参数文件和配置文件中主要物理参数,借鉴文献提供的各参数取值范围,并在抚仙湖模拟中逐个对物理参数进行调试,调试后得到的各参数值见表1.

表1 DYRESM模型主要物理参数
2.3 湖泊水量变化和水量补偿法计算原理
2.3.1 模型中湖泊水量变化计算原理 (1)湖面蒸发量计算
水表面蒸发所需消耗的热量由下式计算[37]:
(1)
式中,Qlh(quantity of latent heat)为Δt时间段内,水表面蒸发所需消耗的热量(J/m2);P为大气压(hPa);CL为10 m参考高度处风速的潜热传导系数(1.3×10-3);ρA为空气密度(kg/m3);水的蒸发潜热(LE)取2.453×106(J/kg)[37];Ua为10 m参考高度处的风速(m/s);ea(vapour pressure of the air)代表水汽压(hPa);es(saturation vapour pressure)为水体表面温度(Ts)条件下的饱和水汽压(hPa);Δt为模型的计算时间步长,模型中时间步长设置为3600 s[37].
因蒸发引起湖泊第N层水体质量变化(kg)的计算公式为:
(2)
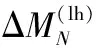
(2)湖面降水量计算
因降水而导致的湖泊水位升高计算公式为:
(3)
式中,rh代表第N层水体由降雨导致的水位变化(m),Rh为日总降雨量(m),Nd为日降雨持续时间(s).
因降水引起湖泊第N层水体质量变化的公式为:
(4)

模型中在Δt时间段内,湖泊第N层水体由蒸发和降水共同引起的总质量变化公式为:
(5)
模型根据公式(1~5),自动完成逐日湖面蒸发量、降水量及其共同导致的水位变化的计算.
2.3.2 水量补偿法计算原理 水量补偿法计算原理如图2所示,首先将模型中逐日出、入流数据均设为0 m3/d,在仅考虑湖面降水和蒸发对湖体库容的影响下,运行模型得到逐日模拟水位;利用水下地形图(比例尺1∶2000)中提供的不同深度对应的面积和体积数据,通过线性拟合构建抚仙湖水位库容曲线,拟合方程为y=2.1634x-3520.3,式中,y为库容(108m3),x为水位(m),相关系数(r)=0.99;基于抚仙湖水位-库容变化曲线,分别计算每日模拟库容和实测库容值,将计算的模拟库容和实测库容从第2天开始相对于前一天的库容值分别求差值,即得到每日模拟库容差值和实测库容差值,计算公式为:
Day(x)实测库容差值=Day(x+1)实测水体积-Day(x)实测水体积
(6)
Day(x)模拟库容差值=Day(x+1)模拟水体积-Day(x)模拟水体积
(7)
式中,x≥1.
将上步骤中计算得到的每日实测库容差值与模拟库容差值求差值,得到的就是模型中每日需要调整的补偿值,即:
Day(x)补偿值=Day(x)实测库容差值-Day(x)模拟库容差值
(8)
补偿值有正有负,正值表明模拟库容低于实测库容,说明模型中入湖水量需增加,故将补偿值补充到入流文件中,一般情况下直接补充到地下水中,反之,说明模型中出湖水量需要增加,将补偿值取绝对值后补充至出流流量,便完成了一次水量补偿计算. 更新出入流文件一次以后,再次运行模型对比模拟水位与实测水位,若误差较小可停止计算,若误差较大则再次使用水量补偿法,计算新的出入流补偿值,再相应修改入(出)流量. 一般运行两次后,即可达到理想效果,完成出入湖水量平衡的计算.
2.4 模型评估标准
模型误差通过计算实际测量值与模型模拟值之间的均方根误差(RMSE)、纳什效率系数(NSE)和相关系数(r)来进行验证[44],其中RMSE和NSE的计算方法为:
(9)
(10)
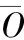
2.5 数据来源
为保证DYRESM模型模拟精度,本文收集了非常详细的有关抚仙湖流域水文、气象和地形等数据(表2),用来进行模型参数率定.
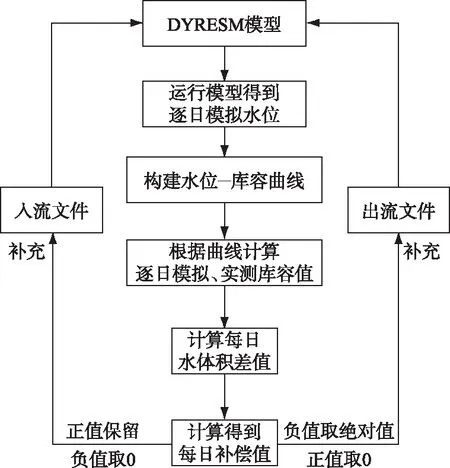
图2 DYRESM水量补偿法计算原理Fig.2 Flowchart of water balancing method for DYRESM

表2 数据汇总*
3 结果与讨论
3.1 抚仙湖入湖水量计算
在出、入湖流量均设为0 m3/d的条件下,模型在仅考虑湖面降水量和蒸发量对库容的影响下,模拟水位呈波动下降趋势,这与抚仙湖年蒸发量大于降水量的结论一致[52](图3a). 经过3次水量补偿计算后,更新出、入流数据,并对模型中逐个物理参数进行调试,再次运行模型得到模拟与实测水位的对比(图3b),对模拟值与实测值进行误差计算,得到RMSE为0.11 m,NSE为0.96,r=0.99,表明经水量补偿法计算和模型物理参数率定后,模型模拟效果良好,并利用率定好的模型,计算出2011-2017年逐日入湖水量.
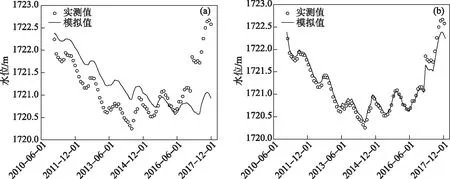
图3 2011-2017年逐月水位模拟与实测对比(a:水量补偿前;b:水量补偿后)Fig.3 Comparison of simulated and measured monthly water levels from 2011 to 2017 (a: before water balancing; b: after water balancing)
本文分别从日、月、年尺度上建立降雨-入湖水量回归方程,发现通过月尺度上建立的回归方程精度最高,故本文利用2011-2017年逐月实测降雨和入湖水量(补偿法计算)数据,建立降雨-入湖水量回归方程. 如图4a所示,回归方程为y=0.0076x+0.85,r=0.71. 用2007年抚仙湖实测逐月总入湖水量对拟合方程计算结果进行验证,实测数据散点和模拟数据散点能够较均匀地分布于1∶1直线两侧(图4b),经误差分析计算得到NSE为0.67,r=0.94. 因此,在入湖水量缺测情况下,通过此回归方程计算得到入湖水量的方法可靠,满足精度要求.

图4 抚仙湖降水量-入湖水量拟合关系(a:拟合方程构建;b:拟合方程验证)Fig.4 Regressed equation between precipitation and inflow volume for Lake Fuxian (a: regression; b: validation)
3.2 DYRESM模型验证

图5 1959-2010年抚仙湖流域 人类活动用水量与农业用水量Fig.5 Water consumption by human activities and agriculture at Lake Fuxian catchment from 1959 to 2010
3.2.1 出湖水量计算 1959-2006年抚仙湖海口河多年出湖水量为9.02×107m3,2007-2010年由于出流改道工程的完成,抚仙湖倒流星云湖年均水量为4.98×107m3,而海口河仅在特殊年份泄洪[49];由于模型中出湖水量以日为单位,且河道出湖水量与降雨之间密切相关,为保证模拟水位趋势的准确性,将河道出湖水量根据研究时段年内各月降水量占年总降水量占比进行重新分配,得到1959-2010年的逐月出湖水量,再在各月内根据天数计算平均值,得到各月份的逐日出湖水量;因1959-2010年跨越的时间尺度较大,且起始年份较早,无详细实测人类活动用水数据,本文通过农业用水量对其进行估算. 根据文献[50]查得1974-2014年抚仙湖耕地面积,利用线性插值法补全1959-2010年抚仙湖流域耕地面积. 据《抚仙湖水环境保护及水污染防治规划》中提供的2007年抚仙湖流域农业用水量和人类活动用水总量可知,农业用水占人类活动用水总量的80.9%,抚仙湖流域耕地的作物类型主要有蔬菜(大蒜、菜豌豆为主)、粮食(水稻、小麦为主)和经济作物(烤烟为主),其种植方式以大小春水旱轮作为主,农业用水主要集中在5-9月(种植水稻、烤烟)和10-12月(种植大蒜、小麦、菜豌豆)[53]. 对此根据2007年耕地面积及对应的农业用水量,通过线性对应关系,在插值得到1959-2010年抚仙湖流域耕地面积条件下,反推其余年份农业用水总量,并在农业用水量占人类活动用水总量比重不变条件下,计算出1959-2010年人类活动用水总量,具体计算结果如图5所示. 将人类活动用水总量中除农业用水量外做日平均计算,将逐年农业用水量平均分配至5-9月和10-12月后做日平均计算,与逐日河道出湖水量相加得到逐日总出湖水量.
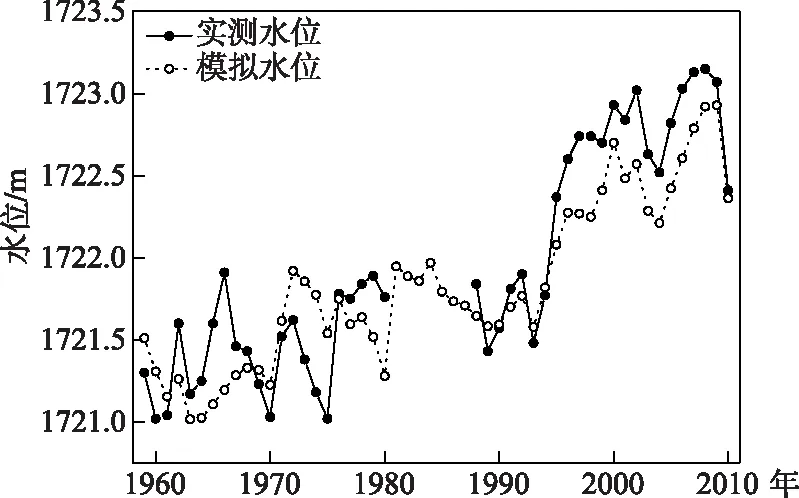
图6 1959-2010年抚仙湖逐年 模拟与实测水位对比Fig.6 Comparison of simulated and measured annual water levels for Lake Fuxian from 1959 to 2010
3.2.2 年际水位变化 在长达52年模拟时长下,DYRESM模型模拟的水位与实测水位变化趋势基本一致(图6). 模拟水位与实测水位间的RMSE为0.4 m,NSE为0.63,r=0.89,模型可良好地反映抚仙湖水位的变化趋势. 模型能有效捕捉到抚仙湖的水位峰值,例如1999年和2008年. 但仍有部分年份的模拟结果不理想,与实测水位有一定偏差,主要出现在1962-1966年和1972-1975年两个时段,误差一方面是在缺少实测入湖水量条件下,根据回归方程计算的入湖水量所造成的;二是由于早期抚仙湖耕地面积数据缺失,采用插值方法计算得出,并反推出湖水量产生了一定误差. 此外,在收集1959-2010年水位数据时,1981-1987年无实测水位数据,本文通过模型计算出1981-1987年多年平均水位为1721.84 m.

图7 1959-2010年水位年内变化特征Fig.7 Inner-annual variation of water levels at Lake Fuxian from 1959 to 2010
3.2.3 年内水位变化 模拟得到的1959-2010年年内水位呈现先下降、后上升再下降的变化趋势(图7). 年内水位最低值(1721.71 m)和最高值(1721.98 m)分别出现在5月和10月,这与贺克雕等[21]分析得到的1988-2015年抚仙湖年内水位变化特征一致,表明模型可有效模拟年内水位变化特征.
3.3 抚仙湖水位预测
影响抚仙湖水位变化的主要因素包括气候变化和人类活动两方面. 气候条件无论从短时间尺度还是长时间尺度上均直接影响水位,人类活动不仅可在短时间内对湖泊水位产生很大的影响,对自然因素还有放大作用. 因此,对湖泊未来水位变化趋势进行预测的基本前提是掌握流域内的未来气候变化和未来人类活动的可能用水量.
3.3.1 未来气候场景选择 全球气候系统模式是进行当代气候模拟和不同排放情景下未来气候变化预估的重要工具. 大量学者[54-55]利用第五次国际耦合模式比较计划(CMIP5)中多种气候模式对云南省及周边地区的未来气候变化展开了研究和预测,结果表明:无论多模式集合、高分辨区域气候模式(如CCLM)还是单气候模式(如FIO-ESM),对于年总降水量的模拟效果均不佳,但能反映降水的季节性变化,且对降水峰值模拟效果较好[55-56];对于气温模拟无论年际还是年内均优于降水模拟效果[57-58];3种气候情景(RCP2.6、RCP4.5和RCP8.5)条件下云南省未来(2021-2050年)气温和降水均呈持续上升趋势,且RCP8.5情景下降水较RCP4.5情景偏多[59].
目前第六次国际耦合模式比较计划(CMIP6)[25]正在有序开展. 相比于CMIP5,CMIP6同时使用共享社会经济途径(SSPs)和典型浓度路径(RCPs)的矩阵框架,并显著提高了大气和海洋模式的分辨率精度[60-61]. CMIP6中4种气候情景[62]SSP126(低强迫情景,辐射强迫在2100年达到2.6 W/m2)、SSP245(中等强迫情景,辐射强迫在2100年达到4.5 W/m2)、SSP370(中等至高强迫情景,辐射强迫在2100年达到7.0 W/m2)和SSP585(高强迫情景,唯一可以实现2100年辐射强迫达到8.5 W/m2的SSP情景)综合考虑了SSPs和RCPs,其中SSP126、SSP245和SSP585分别为CMIP5中RCP2.6、RCP4.5和RCP8.5更新后的情景.
本文采用CMIP6中BCC-CSM2-MR模式的气候预估数据,相比于CMIP5中BCC-CSM1-1模式,该模式对大气辐射、深对流过程和重力波方案等诸多方面进行了改进,使其更适应气候分布[63-64]. 在过去几十年中抚仙湖流域由于气温不断升高,降水呈下降趋势,导致极端干旱事件频发,对此结合各排放情景的特点,在未来情景中选择SSP245和SSP585两个典型气候情景,研究未来(2021-2050年)气温在不同增幅条件下抚仙湖水位变化趋势. 根据云南省边界对全球数据做裁剪和平均处理,并采用初征等[65]提出的数据同化方法,对气象模式数据中的降水、平均气温和太阳辐射等数据进行校正.

图8 基于DYRESM模型预测的抚仙湖 2021-2050年平均水位变化趋势Fig.8 Annual water level for 2021-2050 predicted by DYRESM for Lake Fuxian
3.3.2 抚仙湖未来水位的变化趋势及应对策略 2021-2050年入湖水量采用降水-入湖水量回归方程进行计算;河道出湖流量为0 m3/d;未来人类活动用水量,采用冯海涛等[51]基于抚仙湖最新保护治理政策与未来社会经济的基础上,预测的抚仙湖流域中期(2025年)用水需求量(6.091×107m3)和远期(2035年)用水需求量(6.513×107m3)数据. 将用水需求量数据线性插值处理后补全2021-2050年人类活动用水总量.
利用模型模拟SSP245和SSP585两种情景下,抚仙湖未来(2021-2050年)水位变化趋势(图8). 在SSP245和SSP585两种情景下,抚仙湖2021-2050年平均水位分别为1722.98和1723.93 m,较1959-2017年平均水位1721.77 m分别升高1.21和2.16 m. 两种情景下2021-2040年抚仙湖水位变化趋势均呈先上升后下降的趋势,但SSP585情景下水位要远大于SSP245情景下水位;在2040-2050年期间,SSP245情景下水位呈显著上升趋势,而SSP585情景下水位呈波动下降趋势. 两种情景下模拟水位最高值分别出现在2048和2029年,水位分别为1724.08和1724.75 m;最低值均出现在模拟初始年份2021年,水位分别为1722.12和1722.17 m.
SSP245情景中,在2021-2040年期间,由于降水和气温波动增加,导致水位呈波动变化趋势(图9);2040年后降水增幅显著增加[66],且于2045年达到峰值,气温升温趋势则较为缓慢[54],从而使得湖体蓄水量增加,水位显著上升. SSP585情景中,在2021-2040年期间,其平均降水量显著大于SSP245情景下的平均降水量,其平均气温小于SSP245情景下的平均气温[54,58],故在2021-2040年期间,SSP585情景下的水位要远高于SSP245情景下的水位;而后2040-2050年期间,SSP585情景下升温趋势明显,温度于2045年达到峰值,温度升高使得湖体表面蒸发量增加,导致水位下降[62].
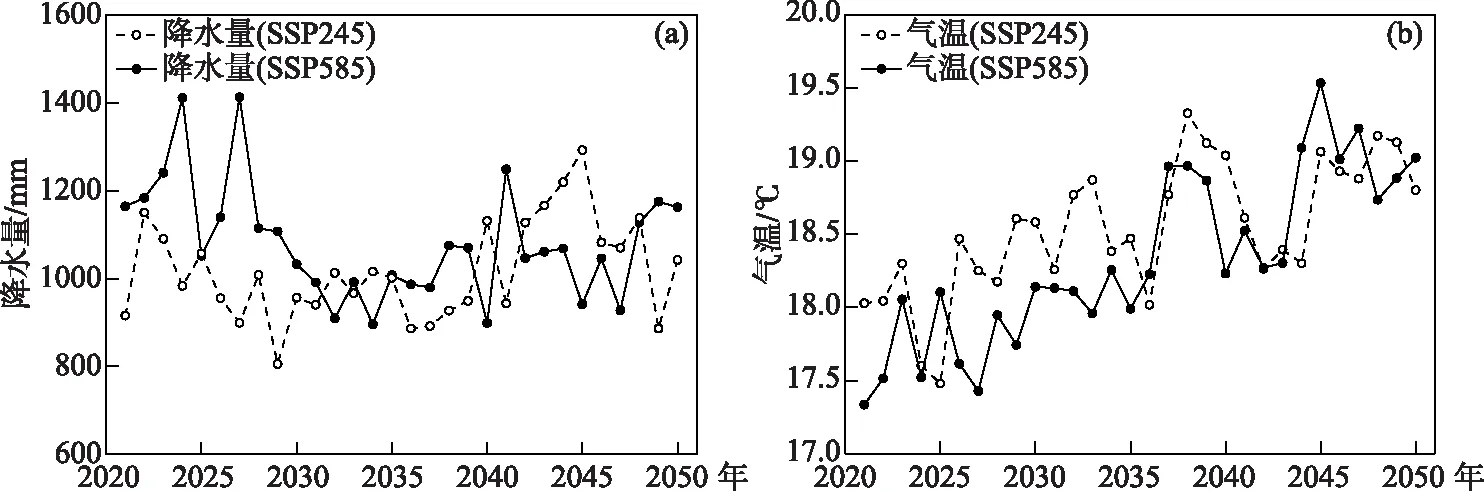
图9 气候模式BCC-CSM2-MR在情景SSP245和情景SSP585下模拟的 2021-2050年平均降水量(a)与气温(b)Fig.9 Annual precipitation (a) and air temperature (b) for 2021-2050 predicted by BCC-CSM2-MR under Scenario SSP245 and Scenario SSP585
在出湖河流流量设为0 m3/d情况下,SSP245情景中未来时段(2021-2044年)抚仙湖水位处于正常蓄水范围,但2045-2050年抚仙湖水位超过法定最高蓄水位(1723.35 m);SSP585情景中未来时段(2021-2024年)水位处于正常蓄水范围,但2025-2050年抚仙湖水位始终高于法定最高蓄水位;两种情景下,抚仙湖未来水位均有部分时段超过法定最高蓄水位,水位过高会破坏湖区原有的生态结构并引起洪水灾害,危害流域内居民生命财产安全. 因抚仙湖为人工调控湖,目前其出湖闸门关闭,当水位接近最高蓄水位时,可开闸泄流至海口河与隔河,以保证水位控制在合理范围内;未来两种情景下水位均高于法定最低运行水位(1721.65 m),水量充足,可满足抚仙湖生态需水、流域内工农业用水和居民生活用水需求.
4 结论
本文运用DYRESM水动力模型对抚仙湖1959-2050年水位进行了模拟,结论如下:
1)构建的降水-入湖水量回归方程精度较高,在入湖水量缺测情况下,可通过此回归方程计算得到抚仙湖的入湖水量.
2)DYRESM模型对抚仙湖水位变化的模拟结果较好,能很好地反映抚仙湖水位的年际和年内变化规律,且能有效捕捉到抚仙湖的水位峰值.
3)模拟结果表明,在SSP245和SSP585两种气候情景下,2021-2050年抚仙湖平均水位均有部分时段超过法定最高蓄水位,但均不低于法定最低运行水位.

