Nonclassicality of photon-modulated spin coherent states in the Holstein–Primakoff realization

Xiaoyan Zhang(张晓燕) Jisuo Wang(王继锁) Lei Wang(王磊)Xiangguo Meng(孟祥国) and Baolong Liang(梁宝龙)

1Shandong Provincial Key Laboratory of Laser Polarization and Information Technology,School of Physics and Physical Engineering,Qufu Normal University,Qufu 273165,China

2Shandong Provincial Key Laboratory of Optical Communication Science and Technology,School of Physical Science and Information Engineering,Liaocheng University,Liaocheng 252059,China

3School of Physics and Electronic Engineering,Heze University,Heze 274015,China

Keywords: the photon-modulated spin coherent state,nonclassicality,photocount distribution,Wigner distribution function

1. Introduction

As a new class of physical carriers, non-Gaussian states play a significant role for many quantum information theory applications. This is mainly because they can improve some important quantum information processes addressing the practical problems of state generation, entanglement and nonclassicality.[1–3]

At present, there has been considerable interest in the engineering of non-Gaussian states, especially, their theoretical and experimental aspects. Both photon-addition and photon-subtraction operations are considered as two kinds of effective methods for producing the non-Gaussian states[4–8]that may provide advantages in metrology and quantum computation.[9–11]The notion of photon addition to a quantum state was suggested by Agarwal and Tara[12,13]and subsequently a number of earlier studies of photon-added and photon-subtracted states was carried out.[14–18]For example, the experimental realization and tomographic analysis of quantum states by adding and subtracting single photon to a classical thermal field have been clarified in Ref.[19]. In addition,the potential usefulness of entangled states concerning precision measurements using entangled input states has been presented.[20]

2. Photon-modulated spin coherent states

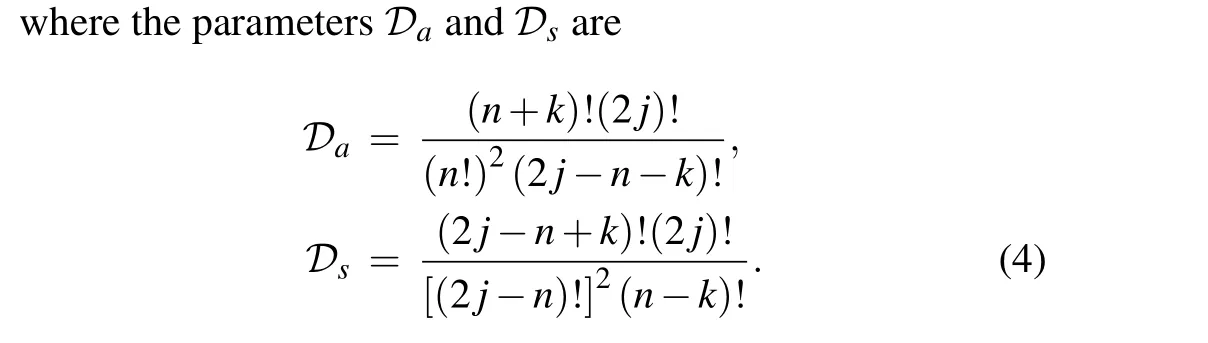
3. Photon number distribution

For the photon-modulated SCSs|z,j〉a(s), their photon number distributions are given as

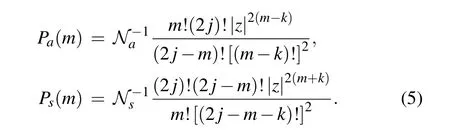
For a given value of|z|(e.g.,|z|=1),we plot the photon number distributionsPa(s)(m)of the states|z,j〉a(s)for different values of the parameterskandjin Fig.1. Figure 1 shows that the photon number distribution only appears in several photon numbers and almost approaches zero for others. With increasing the parameterskandj,the peak of the state|z,j〉amoves to a higher photon numberm,but both a smallerkand a largerjcan lead to a wider photon number distribution. However,for the state|z,j〉s,with increasingjor decreasingk,the peak moves to a higher value of photon number and shows a wider photon number distribution.

Fig.1. Photon number distribution of the state|z,j〉a as a function of photon number m with|z|=1 for(a) j=3,k=1;(b) j=3,k=3;(c)j=5.5, k=3. Photon number distribution of the state |z,j〉s as a function of photon number m with |z|=1, for the same values of |z,j〉a,respectively,refer to(d),(e)and(f).

4. Photocount distribution

Nonclassicality of light fields can be measured using a photon counting apparatus to judge the nonclassical features in experiment,which greatly simplifies the theoretical research of photocount distribution. For a single-mode quantum stateρof light field,the new formula of calculating the photocount distribution is defined as[24]

wherePn-k=Ds|z|2n/Ns. Clearly, Eqs. (10) and (11) show thatPa(s)(m)are the familiar Bernoulli distributions,which indicate that counting the success probability formout ofn±kphotons depends linearly on the probability of countingmphotonsξmmultiplied by the probability of countingn±k-mphotons(1-ξ)n±k-m.

Fig.2. Photocount distribution of the state|z,j〉a versus the number of detected photons m for some different values of k and ξ,with|z|=1,j=3 (a) k=1, ξ =0.1; (b) k=5, ξ =0.1; (c) k=1, ξ =0.99. Photocount distribution of the state |z,j〉s versus the number of detected photons m,with the same values as|z,j〉a,respectively,refer to(d),(e)and(f).

Here we are interested in how the photon counting distributionsPa(s)(m) are affected by varying the parametersξandk,which reveal the variations of the distributionsPa(s)(m)with the quantum efficiencyξof the detector and photon modulated numberk.From Fig.2,we can see that the distributionsPa(s)(m) are related toξandk, only emerge in several numbers of countingm, and are close to zero for others, which indicates that the probability of countingmhas more complicated nonclassical features. For a fixed poor efficiencyξ(e.g.,ξ=0.1),the maximum probability of counting photons gradually decreases and the range being larger askincreases for the state|z,j〉a. However,for the state|z,j〉s,the changes of photocount distributions with the increase ofkare just contrary[see Figs. 2(a), 2(b), 2(e), and 2(f)]. For a fixed modulated numberk(e.g.,k=1),as quantum efficiencyξincreases,the maximum probability of counting photons slowly decreases and its position moves to the large countingmalmost to 0.35 regardless of|z,j〉a(s). In sum,the states|z,j〉a(s)can become more robust and highly nonclassical by modulating the quantum efficiencyξand photon modulated numberk.

5. Second-order correlation function

Fig.3.The second-order correlation function of the state|z,j〉a as a function of amplitude|z|(a) j=3,k=1,2,3;(b)k=2, j=2.5,3.5,5. The secondorder correlation function of the state |z,j〉s as a function of amplitude |z|with the same values as|z,j〉a,respectively,refer to(c)and(d).

6. Wigner distribution

Usually, for a single-mode quantum stateρ, its Wigner distribution is defined asW(α)=tr[Δ(α)ρ], whereΔ(α)=π-1D(2α)(-1)Nis the coherent state representation of singlemode Wigner operator,[26–29]D(2α) = e2(αa†-α*a)is displacement operator andN=a†ais number operator.To obtain the Wigner distributions of the states|z,j〉a(s), we first calculate the normal ordering product of the operatoramD(α)a†n.Inserting the completeness of coherent states into the operatoramD(α)a†nleads to

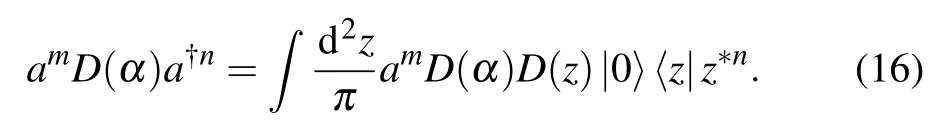
In Fig. 4, we present the Wigner distributions of the photon-modulated SCSs|z,j〉a(s)as a function of Reαand Imαfor different values of photon modulated numberk,spinjand amplitude|z|. Intuitively, the distributionsWa(s)(α)always have negative regions and non-Gaussian features in phase space for certain parameter values, as a signal of the nonclassicality aspect of the quantum state of interest. Specially, the distributionWs(α) of the state|z,j〉sexhibits the multi-peak structure with a main peak and a large negative region in phase space. For small|z|,the distributionWs(α)loses completely its negative region and becomes a single upward Gaussian peak at the central position without the photon modulated numberkand spin numberj, which is similar to the distribution for 2j=k,whereas it exhibits gradually the negative region with increasing|z|. The negative region of the distributionWs(α) increases with increasing integerj, however decreases with the increase of even (or odd)k. On the other hand, for the distributionWa(α), its partial negative region becomes larger with increasingkfor a fixedjand almost keeps unchanged with the spinjfor a givenk. Therefore,photon modulated operation can enhance the nonclassicality of the state|z,j〉by modulating the parametersk,jand|z|.

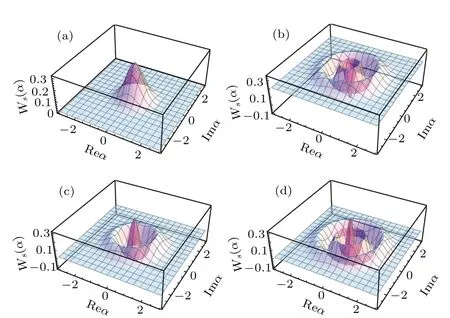
Fig.4. The Wigner function of the state|z,j〉s for different parameters k, j and |z|, where the values of (k, j, |z|) are respectively (a) (2, 2.5,0.01);(b)(2,2.5,20);(c)(3,2.5,20);(d)(2,3,20).

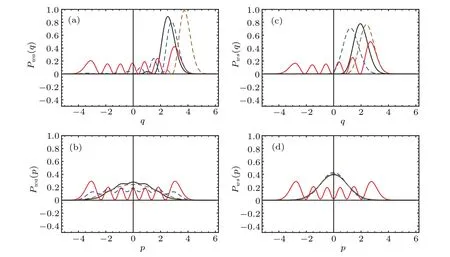
Fig.5. Marginal distributions Pwa(ws) for the functions Wa(s)(α)in the p–q phase space for different values of(j,k,|z|),where(3,1,1,black curves),(3,1,10,red curves),(3,3,1,blue curves),(5.5,3,1,brown curves),respectively.

Figure 5 shows the marginal distributionsPwa(s)(q) andPwa(s)(p)for different values ofj,kand|z|. As seen in Fig.5,the probability distributions only occur in a certain range ofqandpand tend to zero for other ranges. With the increase ofk,the peak of the distributionsPwa(q)andPws(q)moves to the opposite direction along theqaxis,and its peak value decreases. With increasingj, both the peak of the distributionsPwa(q) andPws(q) moves toward the largerq, and its peak value changes are quite on the contrary. In other words, the maximum marginal distribution probability moves to different positionsqwith the changingkandj. On the other hand,we have found that both the states|z,j〉a(s)show probability distributionsPwa(s)(p) with a series of small peaks that have symmetrical feature. Askandjget larger the peak value of the distributionPwa(p)decreases,however the distributionPws(p)is just opposite. Moreover, with increasing|z|, the nonclassical oscillations are enhanced,and the probabilities to detect the particles decrease.

7. Conclusions

In summary,we have repeatedly acted the spin operatorsJ+andJ-on the SCS that leads to theoretically producing two new photon-modulated SCSs,and studied their nonclassical properties via photon number distribution,photocount distribution,second-order correlation function and Wigner function.For the state|z,j〉a,the maximum probability of counting photons gradually decreases askincreases, while it is completely contrary for the state|z,j〉s. Regardless of the states|z,j〉a(s),the maximum probability tends to the large countingmand the value is almost to a fixed value as quantum efficiencyξincreases. Furthermore,using the coherent state representation of Wigner operator, we have obtained the Wigner functions and their marginal distributions for the states|z,j〉a(s)that are always related to Hermite polynomials. The Wigner distributions obviously exhibit the multi-peak structures and some negative regions, which shows that the photon modulated operations can enhance the nonclassicality to a certain degree. Moreover, we have particularly analyzed the peaks of the maximum marginal distribution probability along theqaxis and interference fringes along thepaxis with the different modulated numberskand spinsj. Noting that various types of nonclassicality can be obtained by selecting the appropriate control parameters, and the nonclassicality of the states can remarkably be improved,these results may make the features of the photon-modulated SCSs as a good reference implementation of different schemes of quantum optics and quantum information.

Acknowledgements

This work was supported by the National Natural Science Foundation of China(Grant No.11347026)and the Natural Science Foundation of Shandong Province,China(Grant Nos.ZR2020MA085 and ZR2020MF113).