Ti6554钛合金脉冲电流辅助压缩本构模型的建立及应用

刘斌，武川，周宇杰

Ti6554钛合金脉冲电流辅助压缩本构模型的建立及应用

刘斌，武川，周宇杰

（天津职业技术师范大学 汽车模具智能制造国家地方联合工程实验室，天津 300222）

基于电辅助压缩试验，建立Ti6554钛合金的电辅助压缩本构模型，并对本构模型进行验证。针对Ti6554钛合金材料，在一定脉冲电流参数（电流密度为40、32、24 A/mm2，频率为1、5、10 Hz，占空比为0.7、0.5、0.3）以及应变速率为0.002、0.005、0.01 s−1、下压量为50%的条件下，进行电辅助压缩试验，并基于唯象和物理机制，建立电辅助压缩的本构模型，采用回归拟合的方法确定本构模型参数，得到具体方程，并基于电辅助压缩试验的应力–应变曲线，分析脉冲电流参数对应力–应变的影响规律。将电辅助压缩试验测得的试验值与本构模型得到的预测值进行相对误差分析，得到最大相对误差小于7%。采用回归拟合的方法建立的本构模型相对误差较小，能够准确预测材料在不同脉冲电流参数下的流动应力。

电致塑性；Ti6554；本构方程；脉冲电流

Ti6554（Ti–6Mo–5Cr–5V–4Al）钛合金是一种亚稳定高强韧β型钛合金，因其具有密度小、比强度大、无磁性、强度高等特点，成为制造航空器结构件的重要材料[1-2]。钛合金拥有较高的屈服强度和较低的弹性模量，室温条件下塑性变形范围小，在传统成形过程中变形阻力大、成形性能差，如采用冷冲压法冲压，所需的冲压吨位大，容易开裂，一般采用高温成形和热成形，然而在高温成形和热成形过程中能量损耗大，并且会对材料表面造成氧化进而导致材料利用率低，对模具性能影响较大[3]。鉴于以上因素，发展了一种将脉冲电流引入金属塑性成形过程的成形方式，其原理是在金属成形过程中，利用漂流电子促进位错运动，降低流动应力，提高成形性能，并在一定程度上细化晶粒，从而改善钛合金成形性能，是一种很有前景的成形方法[4-6]。

过去大量科研人员对钛合金热变形过程中的变形行为、组织演化和本构建模进行了系统深入的研究，相关结论对材料变形机理的理解和实际热变形工艺制定起到一定作用。Wu等[7]在Gleeble–3800D模拟机上进行了温度为860～900 ℃、应变速率为0.001～ 10 s−1的热压缩试验，研究了Ti55531合金在β单相区的变形和显微组织演变。王立颖等[8]通过热模拟试验机对Ti–6Al–4V进行热压剪处理，对比分析了不同热机械加工参数下的流变行为和微观组织演变规律。Wu等[9]在回火状态、应变速率为0.001～10 s−1的条件下对Ti55531进行热压缩试验，根据热变形对实测应力进行修正，建立了整个应变范围内的Arrhenius型本构模型。肖寒等[10]通过使用双曲正弦形式修正的Arrhenius本构方程描述了TC4钛合金高温压缩变形时的峰值应力。朱鸿昌等[11]通过材料参数与真应变之间的关系，利用Arrhenius本构方程和参数建立了流动应力和变形温度、应变速率和真应变之间的本构关系。目前国内外研究人员主要针对钛合金热变形宏观和微观变化进行了大量研究，但是针对材料电辅助变形的研究还比较少。

杜引等[12]基于铝锂合金电辅助单向拉伸试验的流动应力曲线，建立了2060–T8铝锂合金电塑性本构方程，进而为制定电辅助铝锂合金成形工艺提供理论依据。张宁等[13]建立了耦合脉冲电流密度和脉冲频率的超塑性本构方程，预测了1420铝锂合金在电致超塑性变形中流动应力的变化规律。彭书华[14]通过分析脉冲电流对金属应力–应变的影响，选择合理的经验方程以简化金属材料的应力–应变模型，得到了脉冲电流对金属应力–应变的影响函数，并结合不同加工硬化模型，提出了新的电致塑性效应本构方程—— H–V模型。尽管针对铝锂合金和铝合金的本构方程的研究较多，但是钛合金与这些材料的变形机理有本质区别，而针对Ti6554钛合金电塑性的变形行为以及本构方程的建立研究较少，因此建立钛合金的电塑性本构方程具有十分重要的意义。文中基于此背景开展了钛合金电塑性压缩本构模型的研究，为后续有限元模拟提供理论和数据支撑。

1 试验

1.1 材料

试验材料采用Ti6554钛合金，其化学成分如表1所示，采用4 mm×8 mm的圆柱体试样，采用矩形方波直流脉冲电源对压缩试样施加电脉冲，方波电源可调节脉冲电流的电流密度、占空比、频率。试验装置及原理如图1所示，由压缩试验机的上下压块为试样提供下压力，电源电极为试样提供脉冲电流，并通过FLIR热成像仪检测其温度变化。

表1 Ti6554钛合金化学成分

Tab.1 Chemical composition of Ti6554 titanium alloy wt.%

图1 电塑性压缩试验装置及原理

1.2 方法

在万能压缩试验机上进行试验。首先在常温不施加脉冲电流时，测得压缩变形量为50%时Ti6554钛合金圆柱试样的屈服极限强度为1 277 MPa，然后进行电塑性压缩试验，在应力达到屈服极限、开始转向塑性阶段时施加脉冲电流，分别测得电流密度为40、32、24 A/mm2，占空比为0.7、0.5、0.3，频率为1、5、10 Hz，测量压缩过程中的应力–应变曲线，具体试验方案如表2所示。

表2 电塑性压缩试验方案

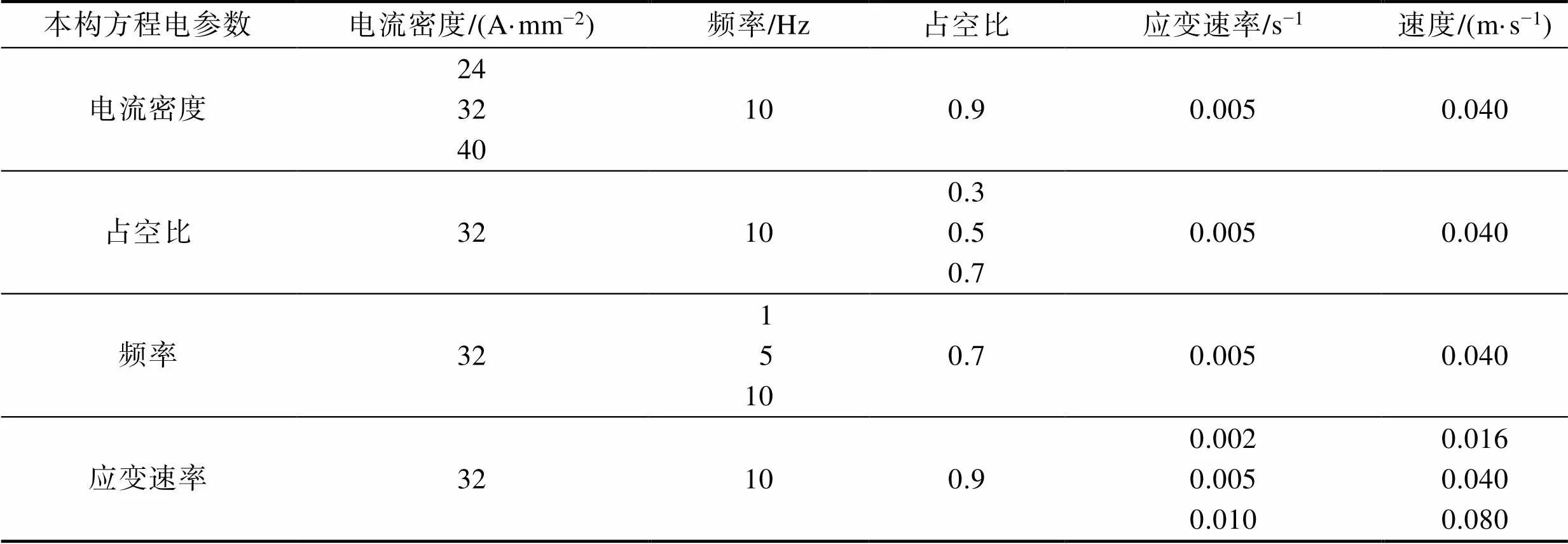
Tab.2 Electro-plastic compression experiment plan

2 结果与分析

Ti6554钛合金电辅助压缩在不同电流密度、占空比、脉冲频率和应变速率下的真实应力–应变曲线如图2所示。可以看出，在塑性阶段加入脉冲电流后，流动应力迅速下降。由图2a可以得出，在相同试验条件下，随着电流密度的增大，塑性阶段的流动应力减小，电流密度为40 A/mm2时的应力最小；从图2b可以发现，脉冲频率对金属的流动应力影响较大，当频率为10 Hz时几乎不产生应力降，当脉冲频率为1 Hz时，塑性阶段流动应力最小，随着频率减小，塑性阶段产生的流动应力减小；从图2c可以得出，当应变速率增大时，塑性阶段的流动应力减小；从图2d可以得出，随着占空比的增大，金属在塑性阶段产生的流动应力减小，当占空比为0.7时，塑性阶段的流动应力最小。

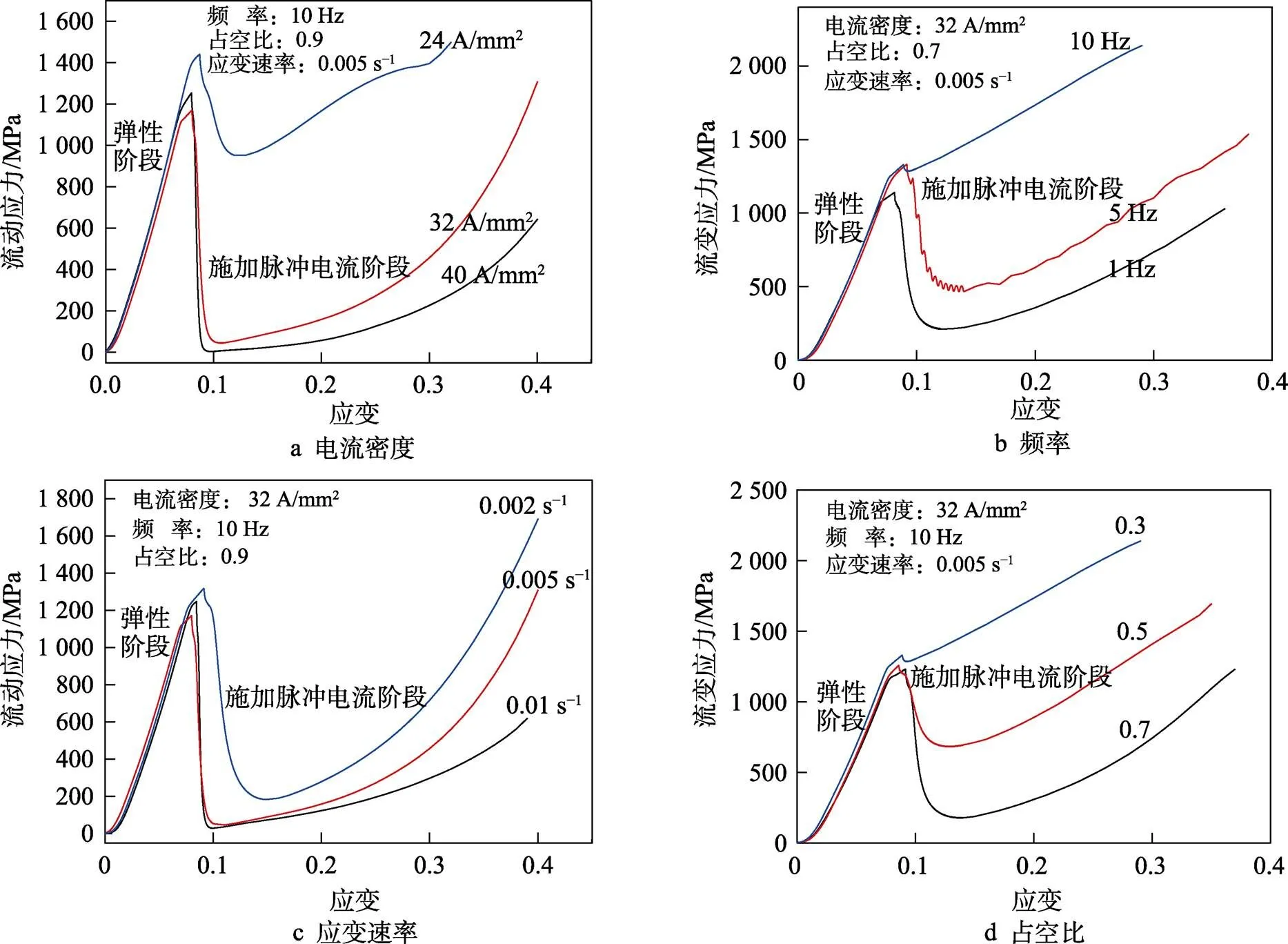
图2 不同脉冲电流因素下的应力–应变曲线

Ti6554的压缩变形进入塑性阶段后，试样的流动应力在通电后迅速下降，随着对试样载荷的加大，应力逐渐升高。这种现象可以通过钛合金塑性变形时内部发生的位错进行解释：压缩过程的弹性阶段没有施加脉冲电流，此时可以发生滑移的位错密度较低，滑移时的动力来源于试样的压缩力，此阶段金属的位错增殖还未发生；当金属的变形进入塑性阶段后，位错密度成倍增殖，脉冲电流可作用的晶界大幅增加，因此在通电的瞬间迅速促进金属塑性流动，宏观上表现为“软化”现象，进而流动应力随之降低[15]。金属通电后，流动应力先迅速降低后逐渐上升，这是因为对试样持续通电会使试样产生温升，发生热膨胀[16]，进而表现为金属的变形抗力升高，流动应力升高。

3 流动应力本构模型建立

3.1 唯象本构模型

唯象模型本构是基于试验数据建立的流动应力与工艺参数之间的数学模型，该模型形式较为简单，不能反映材料变形的物理机制和物理意义。目前常用的本构模型一般不考虑电流密度、占空比、频率这些电参数对变形的影响，文中将电流密度、占空比、频率参数引入唯象模型中，建立钛合金电辅助压缩的变形本构模型。

在金属材料的研究过程中建立本构模型预测应力–应变的变化规律尤为重要，在众多金属塑性研究中，有很多不同形式的本构方程，其中大部分包含金属的变形温度、应变速率、晶粒尺寸等影响因素，而脉冲电流与应力、应变之间的函数关系仍然处于探索阶段。文中基于电辅助压缩实验脉冲电流对应力–应变曲线的影响规律，建立唯象的电塑性本构模型，该本构模型是在Johnson–Cook模型的基础上添加了多个函数来考虑电塑性效应，其中基础的Johnson–Cook模型如式（1）所示。

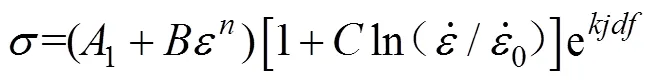
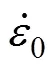
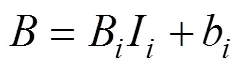
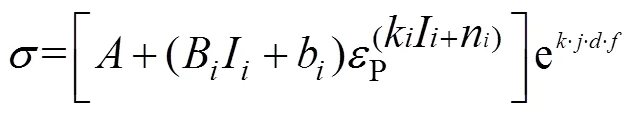
式中：1为电流密度；2为占空比；3为频率；1为电流密度影响下的应变强化系数；2为占空比影响下的应变强化系数；3为频率影响下的应变强化系数；1为电流密度影响下的应变强化常数；2为占空比影响下的应变强化常数；3为频率影响下的应变强化常数；1为电流密度影响下的应变硬化系数；2为占空比影响下的应变硬化系数；3为频率影响下的应变硬化系数；1为电流密度影响下的应变硬化常数；2为占空比影响下的应变硬化常数；3为频率影响下的应变硬化常数；为流动应力。

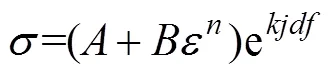
对求解时，不考虑e对的影响，因此将式（5）取对数得到式（6）。

ln()=ln+ln(6)

针对40、32、24 A/mm2电流密度下–曲线，对ln–ln()拟合如图3所示，由式（6）可知，ln为ln与ln()拟合曲线的截距，为ln与ln()的斜率。

由截距ln和斜率得到电流密度1为40、32、24 A/mm2时的应变强化系数和应变硬化指数，根据式（7）在不同电流密度下对应变强化系数与电流密度1进行拟合，如图4a所示，得到1=1 860.71，1=−42 926.72。

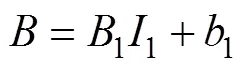
根据式（8）在不同电流密度下对应变硬化指数n与电流密度I1进行拟合，其拟合曲线如图4b所示，得到k1=0.231，n1=−4.86。

式（5）两边取对数后用lnln(A+Bε)除以电参数的乘积，得到电流系数，因此电流密度影响下的电流系数=0.000 023，故得到电流密度的电塑性本构模型如式（9）所示。

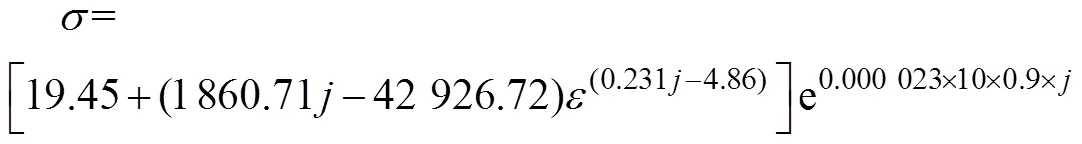
在电辅助压缩试验中发现占空比对流动应力的影响较大，占空比为一个工作周期内，脉冲所占用的时间与总时间的比值。试验方案具体参数如表2所示，采用占空比大小为0.3、0.5、0.7，其余各项参数不变。因此式（4）中当2时，式（4）为针对占空比的电塑性本构模型表达式。对占空比影响的电塑性本构参数进行求解时，用占空比为0.3、0.5、0.7下的曲线，在不考虑e对的影响下，对式（5）中的应变强化系数和应变硬化指数进行拟合，得到lnln(−)拟合曲线如图5所示，因此ln为式（7）中ln与ln(−)的截距，为ln与ln(−)的斜率。

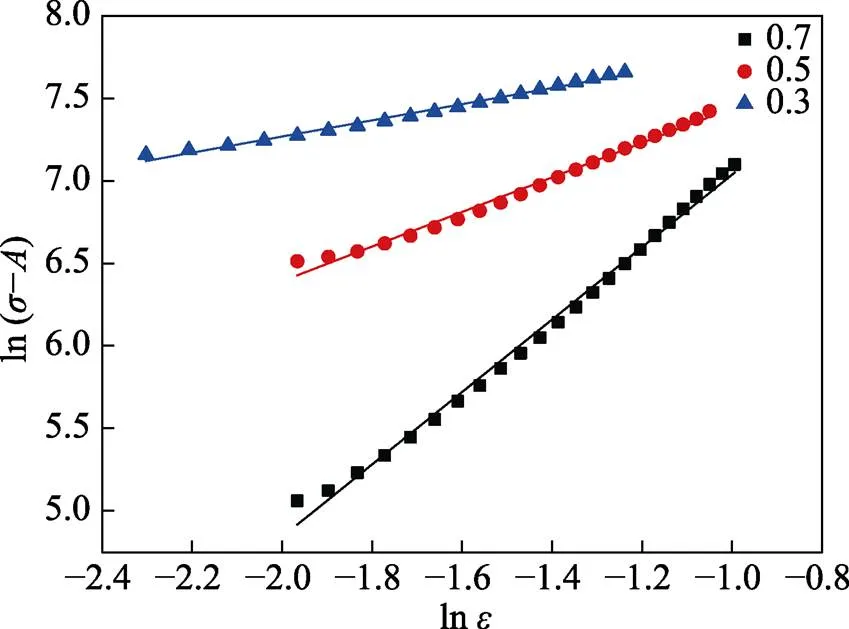
图5 不同占空比下的ln ε与ln(σ–A)拟合曲线

由截距ln和斜率得到占空比2为0.3、0.5、0.7时对应的应变强化系数和应变硬化指数，根据式（10）对不同占空比下的应变强化系数与占空比2进行拟合，如图6a所示，得到2=15 969.95，2=−1 397.90。

根据式（11）对不同占空比下应变硬化指数与占空比2进行拟合，如图6b所示，得到2=4.26，2=−0.85。

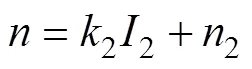
式（5）两边取对数后用lnln(A+Bε)除以电参数的乘积，得到电流系数，因此占空比影响下的电流系数=0.003 9，故得到占空比的电塑性本构模型如式（12）所示。

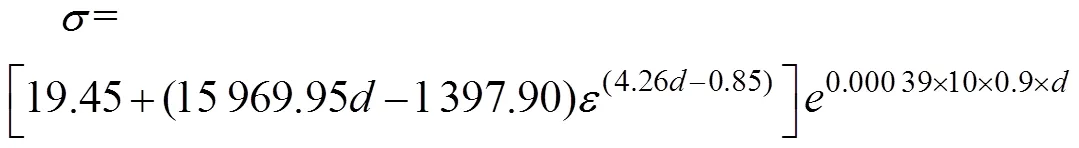
为建立频率的电辅助压缩本构方程，试验方案采用的具体参数如表2所示，频率大小为1、5、10 Hz，其余各项参数不变。因此式（4）中当=3时，式（4）为针对频率的电塑性本构模型表达式。用1、5、10 Hz频率下的曲线对频率的电塑性本构参数求解，在不考虑e对的影响时，对式（5）中的应变强化系数和应变硬化指数进行拟合，得到参数和。对lnln(−)进行拟合如图7所示，ln为式（7）中ln与ln(−)的截距，为ln与ln(−)的斜率。

由截距ln和斜率得到频率3为1、5、10 Hz时的应变强化系数和应变硬化指数，根据式（13）对不同频率下的应变强化系数与频率3进行拟合，如图8a所示，得到3=−267.77，3=6 491.19。

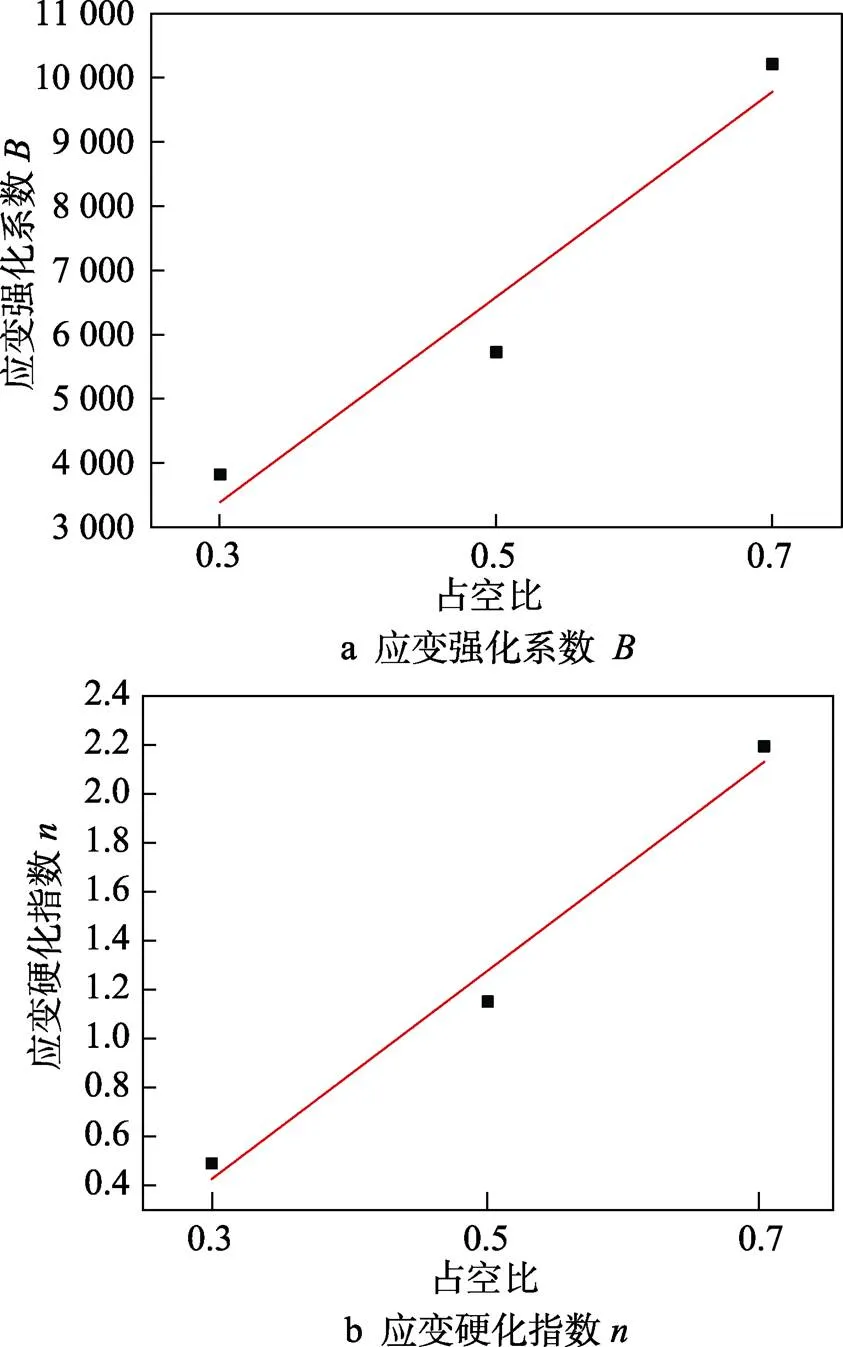
图6 不同占空比下的材料参数和值的确定

图7 针对于占空比的ln ε与ln(σ−A)拟合曲线

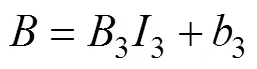
根据式（14）对不同频率下的应变硬化指数与频率3进行拟合，如图8b所示，得到3=−0.143，3=1.942。

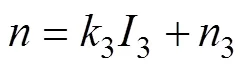
式（5）两边取对数后用lnln(A+Bε)除以电参数的乘积，得到电流系数，因此频率影响下的电流系数=0.004 22，故得到频率的电塑性本构模型，如式（15）所示。

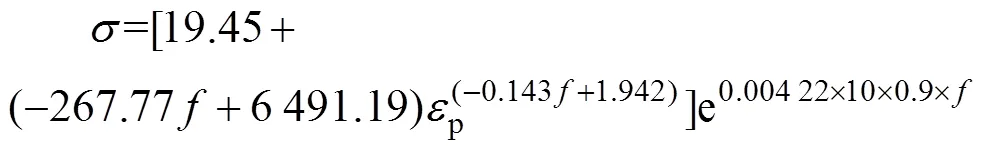
3.2 基于位错密度的物理机制本构模型

鉴于唯象本构模型不能反映相应的物理意义，文中以位错密度为中间变量，建立Ti6554钛合金材料电塑性压缩的物理机制本构模型，以反映钛合金电辅助压缩变形流动应力变化的物理机制。其物理机制是金属在施加脉冲电流后，定向漂流电子加快位错滑移速率，在外力作用下降低了应变速率[17]。施加脉冲电流后的应变速率是由外力压缩产生的应变速率和电塑性效应引起的应变速率同时作用而产生的，根据式（16）可得，在脉冲电流对试样进行压缩试验的过程中，流动应力降低是因为脉冲电流引起金属的应变速率发生变化，在试样压缩过程中应变速率始终不变，在不通电的情况下压缩材料产生的应变速率全部源于外力，在有脉冲电流参与压缩时，应变速率由外力和脉冲电流同时作用而产生变化的，从而宏观上表现为金属的电塑性效应导致流动应力下降。由此可知，位错密度可以从微观角度解释脉冲电流对应变速率的影响，因此文中基于位错密度的物理机制建立应变速率的电辅助压缩的本构模型。

文中对Ti6554在0.002、0.005、0.01 s−1不同应变速率条件下进行脉冲电流的压缩试验，采用的K–M位错密度模型如式（17）所示，设定初始位错密度为6×105m−2，随着应变增加，位错密度也随之递增，每迭代一步应变增加量为0.01，位错密度迭代改变量见式（17），位错密度与流动应力之间的关系见式（18）[18]。

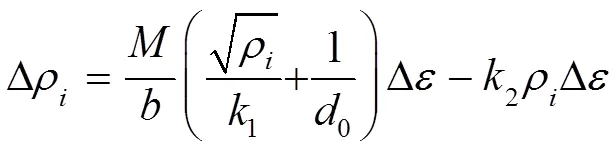
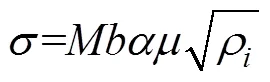
式中：Δρ为位错密度增量；Δ为应变增加量；为泰勒因子，=3.1；为柏氏矢量，=2.86×10−6；ρ为当前位错密度；1为加工硬化系数；2为动态软化系数；1为初始位错密度，1=10−7m−2；为流动应力；为位错间强度，=0.3；为剪切模量，=67 kPa。

在位错密度迭代过程中对参数进行拟合，得到式（19）中1、1、2、2共4个参数的最优解如下：1=424 015.3，1=−348.587，2=1 401，2=−29.918。

3.3 模型准确性验证

3.3.1 唯象本构模型验证

文中所建立的本构方程可以准确预测电流密度为40、32、24 A/mm2，占空比为0.7、0.5、0.3，频率为1、5、10 Hz条件下的流动应力，电流密度本构模型的相对误差=7.3%，频率本构模型的相对误差=5.6%，占空比的本构模型相对误差=6.4%，总体误差小于7%，相对误差计算见式（20），因此唯象本构模型能够准确预测不同电参数下材料的流动应力。为进一步验证本构模型的准确性，对电流密度为28 A/mm2、频率为0.1 Hz、占空比为0.9时的流动应力做出预测，如图9所示，随着电流密度增大，金属的流动应力减小，随着频率的减小，金属的流动应力也减小，随着占空比的增加，金属的流动应力随着减小，由图9可知，基于文中所建立的本构模型预测的流动应力趋势与试验数据相同，符合文中所建立的唯象本构模型规律，能够对圆柱试样电塑性压缩做出较好的预测。

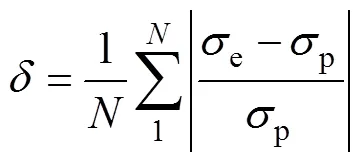
式中：e为峰值应力的预测值；p为峰值应力的实验值；为实验次数。

3.3.2 位错密度本构模型验证

文中基于位错密度所建立的本构模型，可以准确预测应变速率为0.002、0.005、0.01 s−1时的流动应力，总体误差=7.4%，如图10所示，位错密度本构模型具有较高的准确度。为进一步验证位错密度本构模型的准确性，文中在应变速率为0.05 s−1下进行预测，可以得到当应变速率为0.05 s−1时，与电辅助压缩试验具有相同变化趋势，因此基于位错密度的本构模型，能够对电辅助压缩的流动应力进行准确预测。

图10 基于所建位错密度模型对不同应变速率下的流动应力预测

4 结论

1）针对Ti6554钛合金在压缩过程中的塑性阶段对试样施加脉冲电流，使材料在塑性阶段出现较大的应力降。其中电流密度越大、频率越小、占空比越大以及应变速率越小，所产生的应力降越大。

2）采用数学回归拟合的方法建立了电流密度、频率和占空比的唯象本构模型，以及基于位错密度的物理机制本构模型。

3）对建立的本构模型进行验证，其中唯象本构模型误差为6.4%，位错密度本构模型误差为7.4%，总体误差小于7%，因此建立的本构模型对电辅助压缩的流动应力能进行准确的预测。

[1] LI Chang-min, HUANG Liang, ZHAO Ming-jie, et al. Hot Deformation Behavior and Mechanism of a New Metastable β Titanium Alloy Ti-6Cr-5Mo-5V-4Al in Single Phase Region[J]. Materials Science & Engineering A, 2021, 814: 141231.

[2] 武川, 刘斌, 周宇杰, 等. Ti6554钛合金高温变形行为与微观组织演化机制研究[J]. 精密成形工程, 2022, 14(1): 114-125.

WU Chuan, LIU Bin, ZHOU Yu-jie, et al. Investigation on Hot Deformation Behavior and Microstructural Evolution of Ti6554 Titanium Alloy[J]. Journal of Netshape Forming Engineering, 2022, 14(1): 114-125.

[3] LI Xi-feng, JI Bo-yu, ZHOU Qiang, et al. Influence of Grain Size on Electrically Assisted Tensile Behavior of Ti-6Al-4V Alloy[J]. Journal of Materials Engineering and Performance, 2016, 25(10): 4514-4520.

[4] 张昕, 李智军, 李宏伟, 等. 镍基高温合金初始织构对电辅助拉伸宏微观行为的影响[J]. 精密成形工程, 2019, 11(5): 32-36.

ZHANG Xin, LI Zhi-jun, LI Hong-wei, et al. Effects of Initial Texture on Macro-Micro Behaviors of Ni-Based Superalloy during the Electrically-Assisted Tensile[J]. Journal of Netshape Forming Engineering, 2019, 11(5): 32-36.

[5] 江双双, 汤泽军, 杜浩, 等. 钛合金电流辅助成形工艺研究进展[J]. 精密成形工程, 2017, 9(2): 7-13.

JIANG Shuang-shuang, TANG Ze-jun, DU Hao, et al. Research Progress of the Forming Process of Titanium Alloy Assisted by Current[J]. Journal of Netshape Forming Engineering, 2017, 9(2): 7-13.

[6] RUSZKIEWICZ B J, RAGAI I, ROTH J T, et al. A Review of Electrically-Assisted Manufacturing with Emphasis on Modeling and Understanding of the Electroplastic Effect[J]. Journal of Manufacturing Science and Engineering, 2017, 139(11): 110801.

[7] WU Chuan, HUANG Liang. Hot Deformation and Dynamic Recrystallization of a Near-Beta Titanium Alloy in the β Single Phase Region[J]. Vacuum, 2018, 156: 384-401.

[8] 王立颖, 杨友, 刘春兰. 热机械加工Ti-6Al-4V钛合金的流变行为和显微组织演变[J]. 锻压技术, 2020, 45(12): 183-190.

WANG Li-ying, YANG You, LIU Chun-lan. Rheological Behavior and Microstructure Evolution on Ti-6Al-4V Titanium Alloy by Hot Machining[J]. Forging & Stamping Technology, 2020, 45(12): 183-190.

[9] WU Chuan, HUANG Liang, LI Chang-min. Experimental Investigation on Dynamic Phase Transformation and Texture Evolution of Ti55531 High Strength Titanium Alloy during Hot Compression in the α+β Region[J]. Materials Science & Engineering A, 2020, 773: 138851.

[10] 肖寒, 丁平, 张宏宇, 等. TC4钛合金EB炉扁锭高温压缩变形行为和热加工图[J]. 材料热处理学报, 2021, 42(4): 175-182.

XIAO Han, DING Ping, ZHANG Hong-yu, et al. High Temperature Compression Deformation Behavior and Hot Processing Map of TC4 Titanium Alloy Slab Smelted by Electron Beam Cold Bed Furnace[J]. Transactions of Materials and Heat Treatment, 2021, 42(4): 175-182.

[11] 朱鸿昌, 罗军明, 朱知寿. TB17钛合金高温压缩变形行为[J]. 航空材料学报, 2019, 39(3): 44-52.

ZHU Hong-chang, LUO Jun-ming, ZHU Zhi-shou. High Temperature Compression Deformation Behavior of TB17 Titanium Alloy[J]. Journal of Aeronautical Materials, 2019, 39(3): 44-52.

[12] 杜引, 赵亦希, 于忠奇, 等. 2060-T8铝锂合金电致塑性本构方程[J]. 塑性工程学报, 2017, 24(1): 133-139.

DU Yin, ZHAO Yi-xi, YU Zhong-qi, et al. Constitutive Equation of Electroplastic Effect for 2060-T8 Al-Li Alloy[J]. Journal of Plasticity Engineering, 2017, 24(1): 133-139.

[13] 张宁, 张艳苓, 毕静, 等. 1420铝锂合金电致超塑性本构方程[J]. 锻压技术, 2015, 40(5): 63-68.

ZHANG Ning, ZHANG Yan-ling, BI Jing, et al. Constitutive Equation of Electro-Superplastic for 1420 Al- Li Alloy[J]. Forging & Stamping Technology, 2015, 40(5): 63-68.

[14] 彭书华. 电致塑性效应本构方程的研究[J]. 塑性工程学报, 2018, 25(2): 202-206.

PENG Shu-hua. Study on Constitutive Equation of Electroplastic Effect[J]. Journal of Plasticity Engineering, 2018, 25(2): 202-206.

[15] 武伟超, 王永军, 孙宝龙, 等. Al-Cu合金脉冲电塑性效应研究[J]. 热加工工艺, 2014, 43(2): 82-85.

WU Wei-chao, WANG Yong-jun, SUN Bao-long, et al. Study on Electroplastic Effect of Al-Cu Alloy[J]. Hot Working Technology, 2014, 43(2): 82-85.

[16] 杨以鹏. TC4曲面构件自阻加热电塑性成形工艺研究[D]. 秦皇岛: 燕山大学, 2019.

YANG Yi-peng. Study on Resistance Heating and Electro Plastic Forming Process of TC4 Curved Surfaces[D]. Qinhuangdao: Yanshan University, 2019.

[17] 李大龙. 电塑性效应中金属流动应力的理论及实验研究[D]. 秦皇岛: 燕山大学, 2014.

LI Da-long. Theoretical and Experimental Study on Metal's Flow Stress in Electroplastic Effect[D]. Qinhuangdao: Yanshan University, 2014.

[18] YANAGIMOTO J, KARHAUSEN K, BRAND A J, et al. Incremental Formulation for the Prediction of Flow Stress and Microstructural Change in Hot Forming[J]. Journal of Manufacturing Science and Engineering, Transactions of the ASME, 1998, 120(2): 318-322.

Establishment and Application of Ti6554 Titanium Alloy Pulse Current Assisted Compression Constitutive Model

LIU Bin, WU Chuan, ZHOU Yu-jie

(National-local Joint Engineering Laboratory of Intelligent Manufacturing Oriented Automobile Die & Mould, Tianjin University of Technology and Education, Tianjin 300222, China)

This paper is to establish the electro-assisted compression constitutive model of Ti6554 titanium alloy and verify the constitutive model based on the electro-assisted compression experiment. For Ti6554 titanium alloy material, under certain pulse current parameters (current density is 40, 32, 24 A/mm2, frequency is 1, 5, 10 Hz, duty cycle is 0.7, 0.5, 0.3) and strain rate is 0.002, 0.005, 0.01 s−1and the depression amount is 50%, the electro-assisted compression experiment is carried out, and the constitutive model of electro-assisted compression is established based on the phenomenological and physical mechanisms. The constitutive model parameters are fitted with experiment data by the regression fitting method and the specific equation is obtained. Based on the stress-strain curve of the electro-assisted compression experiment, the influence of pulse current parameters on the stress-strain is analyzed. The result shows that the relative error analysis is carried out between the experimental value measured by the electro-assisted compression experiment and the predicted value obtained by the constitutive model, and the maximum relative error is less than 7%.The constitutive model established by the regression fitting method has a small relative error and can accurately predict the flow stress of the material under different pulse current parameters.

electro-plasticity; Ti6554; constitutive equation; pulse current

10.3969/j.issn.1674-6457.2022.05.005

TG306

A

1674-6457(2022)05-0027-09

2021–07–17

国家自然科学基金面上项目（52075386）；中国博士后科学基金面上项目（2020M672309）；天津市教委科研项目（2020KJ107）

刘斌（1996—），男，硕士生，主要研究方向为金属材料塑性成形工艺。

武川（1981—），男，博士，讲师，主要研究方向为金属材料塑性成形工艺。

责任编辑：蒋红晨