基于深度神经网络及隐马尔科夫模型的生猪状态音频识别

彭 硕 刘东阳 时国龙 李广博 慕京生 辜丽川 焦 俊*

(1.安徽农业大学 信息与计算机学院，合肥 230036； 2.蒙城县京徽蒙农业科技发展有限公司,安徽 亳州 233524)

生猪音频包含大量语义，能够体现生猪的行为特征，识别出生猪音频信号中的信息对生猪养殖至关重要。早期的生猪叫声主要靠技术人员人工识别，不仅成本较高，而且效率低下。随着现代信息技术、人工智能、信号处理等技术的快速发展，将音频特征分析与计算机技术相结合能提高效率，有助于养猪业的发展。

目前，对生猪音频的研究已经有一定的进展。在生猪音频的预处理方面，董红松等采用基于离散余弦变换的音频增强算法，对生猪音频中夹杂的风扇噪声去除明显；吴亚文等将改进EMD-TEO倒谱距离的端点检测方法应用到生猪音频信号的端点检测，准确度可达90.293%。在生猪音频的识别研究方面，Exadaktylos等采用模糊C均值聚类算法识别猪咳嗽声，识别率可达85%；Van Hirtum等利用模糊算法对猪声进行分析，准确率为79%；Chedad等提出了一种将咳嗽声与其他声音区别开来的神经网络分类方法，在不同的背景下都有着较高的分辨率；Chung等通过支持向量机对不同疾病的猪声信号进行分类识别，为养殖场猪的患病状况提供了有效参考；刘振宇等使用隐马尔可夫模型对生猪的咳嗽声进行识别，结果表明该模型可完成对猪患呼吸疾病的诊断，识别率为80%；Cho等通过将一维声音信号转换为二维灰度图，带入到卷积神经网络，对猪的消瘦病检测，准确率可达96%；徐亚妮设计了一种基于音频识别技术的母猪咳嗽监测系统,为母猪呼吸系统疾病的早期诊断提供判断依据；黎煊等将双向长短时记忆网络-连接时序分类模型应用到连续猪咳嗽声的检测，准确率达到93.77%；龚永杰使用基于改进MFCC和短时能量与改进的MFCC融合得到的特征参数，构建VQ、SVM和HMM猪咳嗽声识别模型，对猪咳嗽声与非咳嗽声有着较高识别率；李江丽等通过构建支持向量数据描述模型识别生猪咳嗽声，识别率为87.3%；龚永杰等通过改进MFCC并构建矢量量化模型来实现对猪咳嗽声的识别，识别率为94.21%；苍岩等利用MobileNetV2网络对3种状态生猪声音进行分类识别，对异常声音的识别率为97.3%；王文静构建了基于Gradient Boosting、Random Forest以及Extra Trees算法的3种集成学习方法的猪只声音识别模型，对生猪3种状态进行识别。国内外对生猪音频的研究主要集中于猪咳嗽声，对于生猪其他状态下的音频识别研究较少，且考虑的音频种类有限，与需要区分的目标音频一般差异较大，所学习的识别模型对于生猪其他状态下的叫声无法做出识别判断，模型实用性受限。

本研究拟采用基于深度神经网络及隐马尔可夫模型，以期能够有效识别不同状态的生猪音频信号，促进生猪福利化养殖，为生猪智能化健康养殖提供技术支持。

1 材料与方法

1.1 试验材料

本研究运用NanoPc-T4作为主控制器，外接iTalk-02麦克风、USB接口等资源，自主实现声音采集传输的硬件系统。为了获取高质量的单通道音频信号，麦克风采用PCM编码，输出WAV音频格式，通道数设置为1，采样大小设置为8 位，采样率设置为44.1 kHz；试验使用的猪声音频主要源于安徽蒙城京徽蒙养猪场，单独选取较为安静的采样空间，通过声音采集系统，获得10 h的单通道生猪音频，这些生猪音频来自10头成年长白猪，其中3头患有疾病。本研究将采集到的声音划分为5类，包括吃饭声、哼叫声、发情声、嚎叫声、病猪喘气声，所有叫声均通过询问兽医和养殖专家后划分；对采集到的声音样本进行相关预处理操作，最终使用每类300个音频样本作为训练集进行试验，选取每类60个样本作为模型测试样本。

1.2 音频信号预处理及特征提取

为了尽可能减小采集环境中其他噪声对生猪音频信号的影响，需要对采集到的音频信号进行预处理，以便获得较为平稳的音频信号，提取出较好的音频特征，使后续生成的声音模型具有较高的鲁棒性。

1

.

2

.

1

卡尔曼滤波

猪场环境较为复杂，存在着各种噪音，合理的滤波算法对生猪音频的识别至关重要，本研究采用卡尔曼滤波算法对采集到的生猪音频进行滤波降噪，它以线性最小均方误差为最优估计准则，采用状态空间描述法，建立信号与噪声的状态方程，通过前一时刻的估计值与当前时刻的观测值，对状态变量不断修正，并进行相应的预估，利用迭代求得动态系统的滤波结果。具体过程如下：

1)定义一个可由线性随机微分方程描述的离散控制过程的系统以及系统的测量值：

=-1++

(1)

=+

(2)

式中：为

k

时刻的系统状态；为

k

时刻对系统的控制量；和为系统参数；为

k

时刻的测量值；为测量系统的参数；和为被假设成高斯白噪声的过程噪音和测量噪音，它们的协方差为

Q

和

R

。2)利用系统的过程模型，基于上一状态预测当前状态(

k

|

k

-1)：(

k

|

k

-1)=(

k

-1|

k

-1)+

(3)

式中：(

k

-1|

k

-1)为上一状态的最优结果。3)更新协方差

P

：

P

(

k

|

k

-1)=

P

(

k

-1|

k

-1)+

Q

(4)

式中：

P

(

k

|

k

-1)为(

k

|

k

-1)对应的协方差；

P

(

k

-1|

k

-1)为(

k

-1|

k

-1)对应的协方差。4)结合预测值和测量值，得到现状态

k

的最优化估计值(

k

|

k

)：(

k

|

k

)=(

k

|

k

-1)(

z

-(

k

|

k

-1))

(5)

式中：为卡尔曼增益，定义为=

P

(

k

|

k

-1)

/

(

P

(

k

|

k

-1)+

R

)。5)为使得卡尔曼滤波器不断运行下去直至系统结束，还需更新

k

状态下(

k

|

k

)的协方差：

P

(

k

|

k

)=(-)

P

(

k

|

k

-1)

(6)

式中：为单位矩阵；当系统进入到

k

+1状态时，

P

(

k

|

k

)变为

P

(

k

-1|

k

-1)。

1

.

2

.

2

端点检测

由于采集到的生猪音频信号中存在静音段和噪声段，因此需要确定音频信号的起点与终点，以改善数据质量，提高计算效率。本研究借鉴吴亚文等设计的改进EMD-TEO的倒谱距离端点检测算法来实现。主要步骤如下：

1)采用EMD算法将经过降噪处理的生猪音频信号分解成多个单一的模态分量(Intrinsic mode function,IMF)；

2)利用TEO处理有特殊含义的模态分量，获得该模态分量的能量谱，提取出生猪音频的特征频率参数；

3)引入短时倒谱距离方法，计算倒谱距离参数，以获取更为准确的端点值；

4)采取两级参数的端点检测，完成对有效信号开始值和结尾值的辨识。

1

.

2

.

3

信号特征提取

原始信号是不定长的时序信号，在时域上具有较大的冗余度，不利于直接作为学习算法的输入，音频的特征提取将音频信号转换成间接而有逻辑的特征向量，比实际信号更有鉴别性和可靠性。

听觉系统类似于一个滤波器组，对不同频率的声波具有一定的选择性，它们广泛分布于低频信号区，而在高频信号区分布较为稀疏，梅尔频率倒谱系数是通过模仿听觉机理获得的。在对原始猪声信号进行预加重、分帧加窗、快速傅里叶变换(Fast fourier transform,FFT)后，从Mel滤波得到Mel滤波能量并计算其离散余弦变换(Discrete cosine transform,DCT)，形成了反映猪声静态特征的13维MFCC，这里预加重系数选取0.98，帧长和帧重叠时间分别设置为20和10 ms，然后通过添加一阶和二阶差分系数，最终得到39维的MFCC。MFCC提取具体流程见图1。

图1 MFCC声学特征提取流程图Fig.1 Flow chart of MFCC acoustic feature extraction

1.3 声学模型的构建及评测

音频识别系统一般由特征提取、声学模型、语言模型、解码4部分构成，然而语言模型部分在音频识别系统中非必须部分。在构建生猪音频识别系统时，虽然生猪的不同行为状态有着不同的叫声，但它并非一种实际的语言，无法和人类语言相提并论，所以本研究所构建的生猪音频识别系统不考虑语言模型，仅以生猪的声学特征作为研究对象。

1

.

3

.

1

DNN

-

HMM模型结构

隐马尔可夫模型是一种概率统计模型，它描述了两个相互依赖的随机过程：可观察的过程和隐藏的马尔科夫过程，通过对概率的计算，选择最大可能性估计出预测音频的输出序列。深度神经网络是一种具有多层隐含单元的前馈传统人工神经网络。在DNN-HMM框架中，HMM用来描述音频信号的动态变化，DNN用来估计观察特征的概率。

图2示出含有3个隐藏层的DNN-HMM结构，将提取到的音频信号的MFCC特征作为

v

输入层，

v

～

v

为3个DNN的隐藏层，每层包括128个隐藏节点，

v

为输出层，与HMM相连接，HMM包括若干隐藏状态，每个隐状态可以自循环或指向下一隐藏节点。当要计算某个音素的某个状态对某一帧声学特征的观察值概率时，可用该状态对应的DNN输出节点的后验概率表示，由于HMM的解码需要似然概率，而DNN输出的是后验概率，因此需要将后验概率

p

(

q

|

o

)转化为似然概率

p

(

o

|

q

)：

p

(

o

|

q

)=

p

(

q

|

o

)

p

(

o

)

/p

(

q

)

(7)

式中：

p

(

o

)为观察值为

o

的概率；

p

(

q

)为状态为

q

的先验概率；最终得到的声学概率

p

(

o

|

w

)表示为：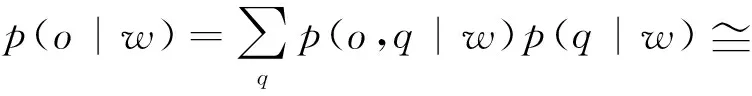

(8)

式中：

w

为维特比算法可能得到的识别序列；

π

(

q

)和

a

-1为由HMM决定的初始状态概率和状态转移概率。

图2 DNN-HMM模型结构图Fig.2 DNN-HMM model structure diagram

1

.

3

.

2

GMM

-

HMM训练

DNN-HMM包括3部分：深度神经网络DNN、隐马尔可夫模型HMM和先验概率分布。由于DNN-HMM与GMM-HMM系统共享音素绑定结构，因此在训练DNN-HMM模型前需要训练一个GMM-HMM系统。因为DNN训练标注是由GMM-HMM系统由维特比算法产生，而标注的质量会影响DNN系统的性能，所以GMM-HMM的初始训练模型非常重要。

GMM-HMM的观察值概率用GMM表示，GMM包含多个高斯函数，即概率密度函数(Probability density function,PDF)，因此需要对起始概率、转移概率、各状态不同的PDF的权重、各状态中不同PDF的均值和方差进行重估。由于音频识别采用自左向右结构的HMM，因此起始概率设置为：[1,0,0,…，0]，即只能从第一个状态开始训练。结合HMM的前向后向算法，定义如下统计量：

(9)

式中：

α

(

j

)为前向概率，即在时刻

t

隐状态为

q

下，观察序列为{

o

,

o

,…，

o

}的概率；

β

(

j

)为后向概率，即在时刻

t

隐状态为

q

下，从

t

+1时刻到最后

T

时刻的观察序列为{

o

+1,

o

+2,…，

o

}的概率；

c

为和状态

s

关联的观察值被分配到高斯分量

k

的比重；

G

为高斯函数,参数为

t

时刻的观测特征以及对应的均值和方差；

p

(

o

|

λ

)为边缘概率分布；

π

为状态

s

下的初始状态概率；

a

为转移概率，不受GMM影响；为权重。结合HMM和GMM的重估计公式，基于最大似然(Maximum likelihood,ML)准则，使用Baum-Welch算法，GMM-HMM参数的最大期望(Expectation-maximization,EM)重估计公式为：

(10)

(11)

(12)

(13)

式中：

T

为训练样本数

C

的时间；表示在

t

时刻隐藏状态为

s

而

t

+1时刻隐藏状态为

s

的概率。

在此过程，设置合适的迭代次数和阈值，在模型收敛或达到最大迭代次数时，得到已经训练好的GMM-HMM模型。

1

.

3

.

3

有监督的DNN训练在DNN-HMM模型中，DNN用于模拟在给定的输入观察状态条件

o

下HMM隐藏状态

q

的后验概率。把GMM-HMM中的HMM提取出来作为DNN-HMM中的HMM部分，GMM用DNN替换，将上一节由训练GMM-HMM模型生成的参数标签作为DNN的输入。选择合适的激活函数,由式(14)产生输出向量：=

f

()=

f

(-1+),0<

l

<

L

(14)

式中：=-1+为激励向量；-1,,分别为激活向量、权重矩阵、偏差系数矩阵；

L

为神经层的数目；

f

(·)为对激励向量进行元素级计算的激活函数。通过误差反向传播算法，选取合适的损失函数，更新权重和偏移量。将输出层的误差依次往隐藏层到输入层传播，实现损失代价的逐层传递，并在每层分别调整权重和偏移量参数，直到期望损失函数值几乎不更新，达到最小化的收敛状态为止，权重和偏移量的更新由式(15)和(16)确定：

(15)

(16)

式中：

η

为学习率；和分别为第

t

次迭代更新后的

l

层的权重矩阵和偏置向量；和为在

t

+1次训练中获得的DNN模型参数；

J

为交叉熵损失函数(Cross entropy,CE)，计算公式为：

(17)

式中：

i

为输出层节点索引；为真实标签，由GMM-HMM模型生成；

y

为其激活函数；为第

t

次迭代时对第

l

层的平均权重矩阵梯度和平均偏置向量梯度。

1

.

3

.

4

猪声声学模型的构建及测试

将提取生猪音频样本的39维梅尔频率倒谱系数作为音频特征，并利用其构建DNN-HMM模型。具体过程如下：

1)GMM-HMM的训练。根据先验知识，使用5种隐藏状态来模拟生猪的吃饭声、发情声、哼叫声、嚎叫声以及病猪的喘气声的音节，初始概率长度的给定与状态数相同，首元素为1，其他元素为0；将隐状态转移概率矩阵设置为5×5，总值为1；通过均匀分割猪声特征训练样本，估计其全局均值和方差来初始化观测状态转移概率矩阵。采用Baum-Welch算法进行GMM参数优化重估，通过维特比算法获得对齐信息来更新HMM参数。在此过程中，设置迭代次数为40，收敛阈值为10，完成此过程后，基于GMM-HMM系统，实现了训练音频的数据帧与对应音节的相应状态上的对齐。

2)有监督的DNN训练。把已经完成帧与隐状态对齐的数据标签导入到DNN中，为减少网络冗余，将splice设置为3，即取当前帧的前后3帧，拼成一个7帧的向量，利用相邻帧的信息对上下文特征之间的相互关系进行建模。考虑到训练的音频数和特征维数，设置含有3个隐藏层的神经网络，为了加快计算，每层设置128个节点,设置softmax层作为输出层，经过前向传播得到输出概率，并与1)获得的训练标签计算误差损失。整个过程中，激活函数使用整流线性单元(ReLU)，其表达式为：

f

=max(0,

z

)

(18)

式中：

z

为全连接网络的输出。损失函数使用交叉熵损失函数。通过误差反向传播算法更新权重和偏移量。设置初始学习率为0.003，设置验证集的数据的比例为0.1，为了加快训练计算，将epoch设置为10，batch_size设置为100，最大迭代次数设置为200，收敛阈值设置为10，使用自适应矩估计(Adaptive moment estimation, Adam)优化算法调整学习率；为了防止过拟合，使用早停法(Early stopping)，当模型在验证集上的表现开始下降的时候，停止训练。从生猪音频验证集的准确度(图3)和损失值(图4)变化可以看到，在多次迭代后，DNN的训练损失不断下降，模型验证准确度也不断增大，最终损失值约为0.04，准确率约为93.5%。

图3 生猪音频验证集准确率的变化Fig.3 Variation of accuracy of live pigs audio validation set

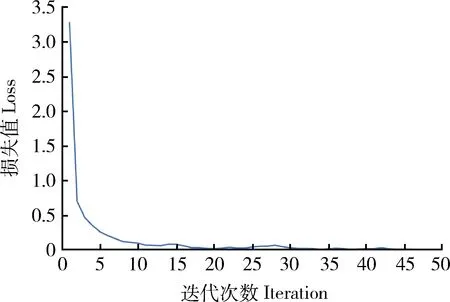
图4 生猪音频验证集损失值的变化Fig.4 Variation of loss value of live pigs audio validation set

3)模型测试：在已经训练好DNN-HMM模型后，对几种生猪行为状态对应的测试音频样本进行MFCC特征的提取，将提取的特征输入到训练得到的5个声音模型

λ

=(,,),(

n

=1,2,…,5)中，通过维特比算法搜索测试样本在识别模型中的最佳隐藏状态转移路径并计算累积输出概率，比对在测试样本在5个模型中的输出概率大小，获得声音的识别结果。

1

.

3

.

5

性能测试指标

音频识别系统的优劣采用识别率评价，本研究使用正确率和平均识别率作为性能测量的指标，正确率是相对音频某一类别而言，平均识别率相对音频总数而言。计算公式为：

正确率

(19)

平均识别率

(20)

2 结果与分析

2.1 猪声样本的预增强

为了减少猪场排风扇、鸟鸣声以及录音设备工作时的电流声等噪声信号对生猪音频识别的影响，将数据样本进行滤波降噪处理。图5示出猪场环境噪声频谱及试验生猪5种状态下的音频信号频谱图，可见，噪声信号的频带主要在3 kHz以下，而生猪5种状态下的音频信号，即吃饭声、发情声、病猪喘气、嚎叫声、哼叫声的频带分别为0～6、0～9、0～14、0～6、0～4 kHz，与噪声信号有所重叠，因而传统的数字滤波器(低通、高通或带通)难以有效去除噪声。由于没有极为纯净的生猪音频作为衡量标准，本研究事先运用MATLAB对滤波算法的性能进行了考察，经过对比，最终采用卡尔曼滤波算法实现对5种生猪音频的去噪，图6为经过滤波前后的音频信号波形图，滤波后的音频信号失真较小，且经人工主观试听，去噪效果良好。

采用改进的EMD-TEO倒谱距离的端点检测算法截取合适的非静音段音频，并进行特征提取，使用提取到的39维MFCC特征，构建音频识别模型。

图5 猪场噪声及5种生猪音频的频谱图Fig.5 Frequency spectrum of pig farm noise and five kinds of pig audio

2.2 猪声声学模型测试结果及对比分析

为验证DNN-HMM模型在猪声识别方面的可靠度，本研究将5种经过滤波处理后的生猪音频在GMM-HMM和DNN-HMM 2种模型下的识别率进行比较，结果按百分比显示，使用混淆矩阵(Confusion matrix)展示，结果见图7。可见：GMM-HMM对5种生猪音频，即吃饭声、发情声、病猪喘气声、嚎叫声和哼叫声的识别率为65%、50%、65%、90%和60%；而DNN-HMM对相应的生猪音频信号的识别率为70%、80%、95%、95%、75%。总体而言，GMM-HMM对5种行为的猪声平均识别率达到66%，DNN-HMM对5种行为的猪声平均识别率达到了83%。DNN-HMM较GMM-HMM在吃饭声、发情声、病猪喘气声、嚎叫声和哼叫声上识别率分别提高了5%、30%、30%、5%和15%，总体平均识别率提高了17%。

由于DNN能学习到深层非线性特征变换，且在本研究中对DNN训练时引入帧的上下文信息，所以相对于GMM的识别有所提升。对于有些复杂度较低的音频信号，原本的GMM-HMM识别率已经很高，因此采用较为简单的深度神经网络结合隐马尔可夫模型在音频识别上的提升度比较有限。对于一些复杂度较高的生猪音频，考虑到训练测试的生猪音频样本数量较少，且仅以梅尔频率倒谱系数作为音频的声学特征，所以对于不同的状态音频识别率可能有所差异。后续将加大样本数量，并结合其他的特征参数作为网络的输入，对生猪音频的识别做进一步研究。

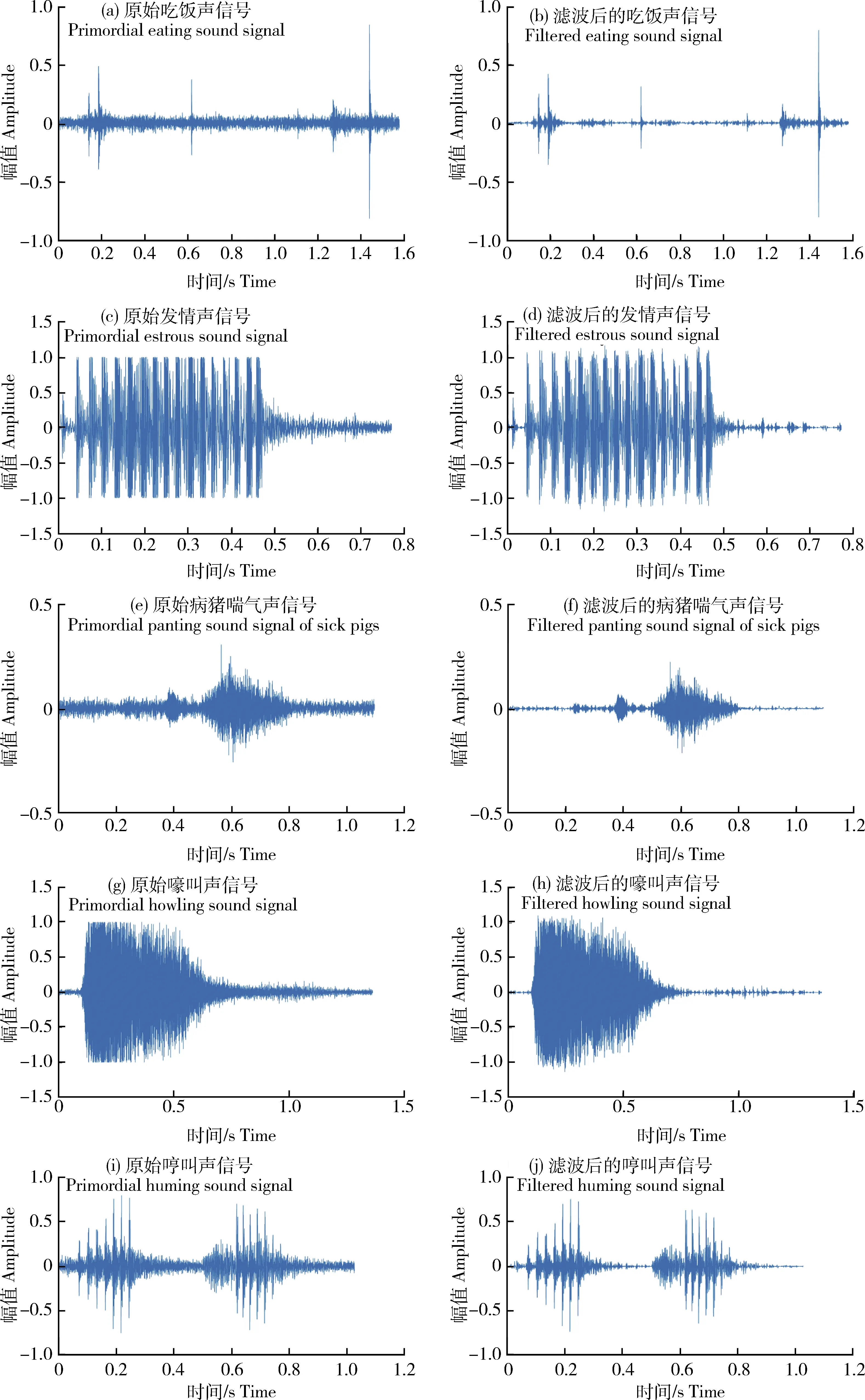
图6 语音增强前后波形对比图Fig.6 Waveform contrast before and after speech enhancement

图7 5种生猪音频在2种模型下识别的混淆矩阵Fig.7 Confusion matrix for recognition of five kinds of pig audio under two kinds of models

3 结 论

本研究使用深度神经网络代替传统音频识别模型中的高斯混合矩阵成分，结合隐马尔可夫模型，提出了一种新的猪声识别方法。将采集到猪声用卡尔曼滤波器降噪，提取梅尔频率倒谱系数，利用HMM用来描述音频信号的动态变化，DNN用来估计观察特征的概率，将生猪音频对应的特征参数作为观测序列，决定生猪音频的音素作为隐状态，构建DNN-HMM的猪声识别系统。试验表明，该模型在几种猪只声音的识别中效果良好，各方面相对于传统的GMM-HMM模型都有所提升，总的识别率提高了17%，对于生猪音频识别和行为状态的判定具有较高的实用价值。