稀疏BP神经网络对房租价格影响因素的探究——以长沙市中心城区为例

姚 菲

（广西师范大学数学与统计学院，广西 桂林 541006）

一、引言

随着网络技术的快速发展，高维数据出现在了生活中的各个领域，但并不是所有变量都是有价值的，这时变量选择成为了高维数据建模必不可少的一部分，如何去选择变量一直以来都是人们讨论的焦点。

Tibshirani在1996年提出了一种变量选择的方法LASSO，对模型系数施加L1惩罚，使不重要变量的系数压缩到0，完成变量选择；带L1惩罚的稀疏神经网络方法已被广泛的应用和证明；将变量选择的方法运用到实例中，李春林等利用LASSO回归和XGboost模型分析了影响石家庄市房租价格的重要因素；田坤瑞在对北京市房租价格影响因素建立普通线性回归模型的基础上，考虑空间的非平稳性添加空间权重，建立地理加权回归模型，效果比普通线性回归模型更好；郭茹梦探究了北京市合租房价格的影响因素，将随机森林和XGboost模型的预测性能进行了比较，XGboost模型的预测效果更好，并对变量重要性进行了排序；张英婕等将房屋的基本信息、GIS数据和周边环境的POI数据相结合，建立多元线性回归模型探究房租价格的影响因素；范雅静等对北京市房租价格影响因素建立广义线性模型进行研究；李英冰等基于武汉市二手房的区位特征、建筑特征和邻里特征构建BP神经网络模型，预测二手房价格效果良好；刘洋用BP神经网络预测北京市二手房价时，在房屋基本信息的基础上增加了百度地图API的信息，得出预测的准确性有所提高。

房价一直居高不下，许多年轻人因为买不起房，而选择了租房这一生活方式。长沙市作为湖南省省会，有大批的年轻人来到这里寻求工作岗位，租房需求量较大，探究房租价格的影响因素，有利于政府对租房市场更好的管控，提高人民的幸福感。在已有的研究成果中，对房租价格影响因素的研究非常少，大多数构建的都是线性模型，而影响房租价格的因素错综复杂，房租价格可能呈现非线性变化，这时传统的线性模型拟合出来的效果可能不佳，而BP神经网络具有极强的非线性逼近能力，对模型的要求不高，是目前最常用的神经网络模型之一。本文建立稀疏BP神经网络模型，探究影响长沙市中心城区房租价格的重要因素。

二、稀疏BP神经网络模型

房租价格的影响因素众多，并不是所有的因素都对其有重要作用，本节将介绍稀疏BP神经网络模型，该方法能对候选指标进行变量选择。BP神经网络是一种按误差逆传播算法训练的多层前馈网络，它由输入层、隐藏层和输出层构成，三层BP神经网络如图1所示。当学习样本输入后，信息经由各层向输出层传递。之后根据减少目标输出与实际输出误差的原则，从输出层反向经过各层至输入层，逐级修正各连接的权值。m层神经网络公式如1式所示。

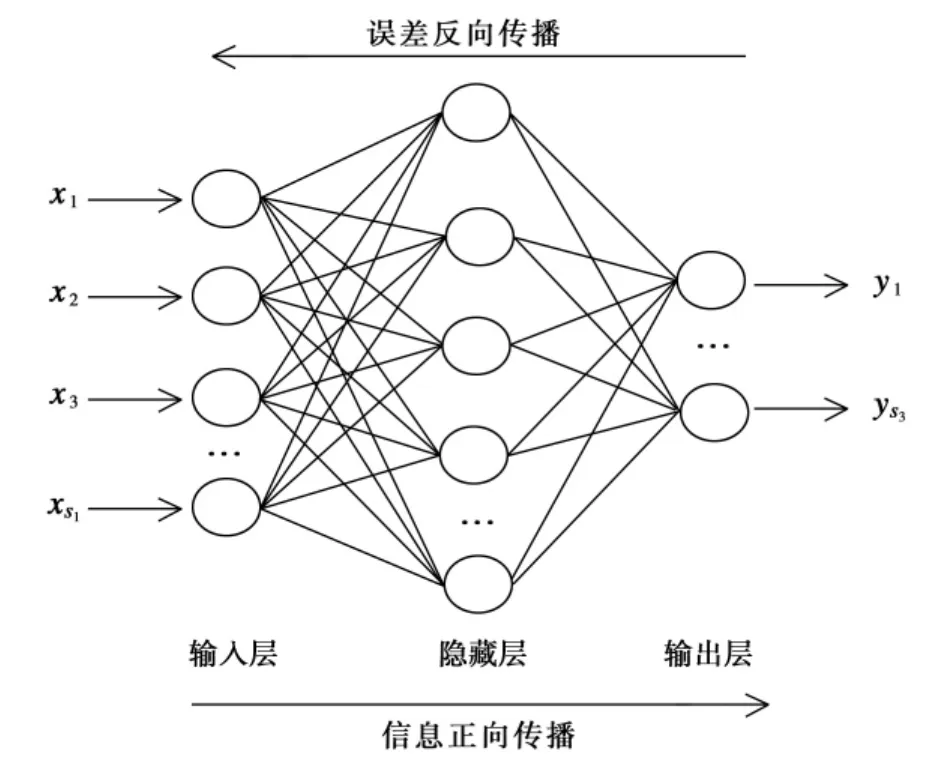
图1 三层BP神经网络

在数据是高维的情况下，如果把所有变量都引入到模型中，参数过多，模型过于复杂容易造成过拟合，变量选择是建模过程中非常重要的一步。对神经元权重施加L1惩罚，如2式所示，梯度下降是近似求解使得权重压缩不到0，但可以将不重要变量的权重压缩至很小，从而起到变量选择的作用。

定义输入层自变量集合x=（x，x，x…x），提取输入层到隐藏层的所有权重，进行如3式所示的计算，得到各自变量的权重相加值，多次模拟后设置一个阈值p，如果a＜p，k∈（1，2，3…s）视为将其压缩至0，剔除自变量x，完成变量选择。

三、正态数据模拟

模拟生成服从标准正态分布的样本数据集，样本数为10000，变量个数为1000，假定真实模型为：

其中，ε～N(0，1)与x相互独立，一般来说神经网络模型越复杂，结果准确度越高，但增加了训练时间，容易导致过拟合现象的出现。将稀疏BP神经网络的层数设置为三层，包含一层隐藏层，构建一个1000-3-1的稀疏BP神经网络，激活函数均选择tanh函数。设置迭代次数epochs为100，每500个样本进行一次权重更新，loss函数采用均方误差，L1正则化的学习率设置为0.1。

将数据集打乱，对其按8:1:1的比例划分为训练集、验证集和测试集。构建稀疏BP神经网络模型，进行100次训练，完成如3式所示的计算，设置阈值为0.01，变量的权重相加值小于阈值，视为将其压缩至0，剔除该变量完成训练。其训练集和验证集的损失函数值如图2所示，可见训练集和验证集的损失函数值接近重合，并且在不断减小，最后趋于平稳，稀疏BP神经网络达到一个比较良好的训练性能。

图2 训练集验证集损失函数值

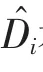
结果如表1所示，错误选择率和负选择率的值均为0，说明稀疏BP神经网络模型具有良好的变量选择性能，均方预测误差和均方拟合误差都较小，说明其预测和拟合效果也非常不错。

表1 模型性能结果表

四、房租价格影响因素探究

（一）数据来源与处理

贝壳找房网是一个为消费者提供包括二手房、新房、租赁和家装等全方位居住服务的平台。利用python对贝壳找房网上长沙市中心城区的租房信息进行爬取，由于网站只显示100页，所以分别对雨花区、岳麓区、天心区、开福区、芙蓉区的租房基本信息进行爬取，周边环境如1km以内的地铁医院数量等信息通过百度地图API获得，返回的结果最大为10，但实际数量可能比10更多，共爬取到9267条数据。比对以往的文献资料，结合贝壳找房网上显示的信息，房租价格作为因变量，选出以下18个指标作为自变量进行研究。

由于爬取出来的数据存在缺失、重复和未知的现象，为了更好地进行后续研究，对原始数据进行如下处理：对重复的租房信息进行删除处理；对指标存在大量缺失的租房信息进行删除处理；存在16条租赁方式未知的租房信息，房租都在2500元以上判断为整租；用水用电燃气情况存在大量暂无数据的租房信息，直接删除会导致数据分布发生偏差影响结果的准确性，故将暂无数据记为0。最后整理出7943条租房信息。

表2 候选指标说明

如图3所示，房租价格大多集中在1000-4000元之间，2000-3000元附近分布最为密集，呈现偏态分布。对其进行对数化处理，使数据更加平稳，消除异方差性便于计算。

图3 房租价格频数柱形图

数据集中不同属性的变量量纲不一致，会影响结果的准确性，利用6式对数据集进行归一化处理，将数据范围控制在[0，1]之间，尽可能消除外界因素对结果的影响。将数据集打乱，对其按8:1:1的比例划分为训练集、验证集和测试集。

（二）参数设定

将稀疏BP神经网络的层数设置为三层，输入层的节点数应与自变量个数相匹配即为18，输出层的节点数应与因变量的个数相匹配即为1，确定隐藏层节点数的经验公式如7式所示。其中a为输入层节点个数，b为输出层节点个数，c为常数，取值范围在1-10之间，则隐藏层节点数取值范围应在5-14之间。

对含不同隐藏层节点数的稀疏BP神经网络分别进行10次测试，训练误差取10次的均值比较其结果，如表3所示，节点数为8时，平均训练误差最小，则设置隐藏层节点数为8个。激活函数均选择relu函数。

表3 训练误差比较表

（三）稀疏BP神经网络的训练

设定好以上参数后，每次训练进行100次迭代，每500个样本进行一次权重更新，loss函数采用均方误差，L1正则化的学习率设置为0.01。完成稀疏BP神经网络的训练之后，进行3式所示的计算，得到18个自变量的权重相加值，进行100次模拟，设置阈值为0.01，变量权重相加值小于阈值视为压缩至0，剔除该变量。权重相加值小于阈值的变量，即被剔除的变量如下表所示，可以看出所属地区、楼层、朝向、用水情况、用电情况、1km以内小学数量、1km以内中学数量这7个变量的权重相加值每次都小于阈值，故将这7个变量剔除。

对于剩下的11个自变量，将权重相加值进行从大到小排序，分别为租赁方式、卫生间数量、卧室数量、客厅数量、面积、是否精装修、有无电梯、1km以内地铁数量、1k m以内医院数量、1k m以内商场数量、有无燃气。

表4 100次模拟被剔除变量

可见房屋属性的指标对房租价格的影响最大，人们在租房的时候首要考虑的还是房屋本身的构造；配套设施影响最大的是有无电梯，电梯是高楼层的必备，后期的维护也需要一定的费用；周边环境影响最大的是1k m以内地铁数量，地铁快捷方便不会拥堵，是大城市中人们出行的主要方式之一，租房时交通是否便利是人们非常关注的方面。

五、结论

本文基于稀疏B P神经网络探究了长沙市中心城区房租价格的影响因素，找出了影响房租价格的重要指标。首先利用模拟生成的标准正态数据，从错误选择率、负选择率、均方预测误差和均方拟合误差这几个指标说明了该模型在变量选择、预测和拟合性能方面的优良性。将该模型引入到实例应用中，探究影响长沙市中心城区房租价格的重要因素。

在房屋属性方面，租赁方式、房屋户型、面积和是否精装修对房租价格有着重要影响，而租房不同于买房，能够随时变动自由性大，所以房屋的楼层和朝向是人们较少关注的，房东在进行住房改造的时候可以着重考虑这几点，加快房屋的出租速度；在配套设施方面，有无电梯和燃气对房租的影响更大，用电用水情况对房租影响较小；在周边环境方面，1k m以内的地铁医院商场数量对房租价格影响更大，地铁越多说明交通越便利，商场越密集说明人流量越大，医院也是生活中必不可少的一部分，政府可以加强城市郊区的房屋周边配套设施建设，改善租户的居住环境，大部分租房的群体都是没有孩子的年轻人，对教育的需求不大，所以1k m以内的中小学数量对房租价格的影响很小。随着越来越多的人涌入大城市，租房需求量不断增加，政府应该出台更多的政策规范租房市场，抑制房租的快速上涨，提高人民的生活满意度。

本文研究还存在相应的不足：变量选择的方法还有S CA D、Elastic Net等，可以将这些方法引入到B P神经网络中进行变量选择；房租会受到时间的影响，例如毕业季租房的需求量大增，而数据仅来源于2021年11月的某段时间存在局限性，可以加大时间的跨度；本文只研究了18个指标对房租价格的影响，租金的影响因素还有很多，在未来可以加入更多的指标进行研究。