考虑订单合并和货物转运的多式联运路径优化研究
李兆进, 刘 雅, 杨 臻
(西安交通大学 管理学院,陕西 西安 710049)
0 引言
随着电子商务的飞速发展,零担物流企业每个时刻需要服务的订单数量迅速增长[1]。除了订单数量庞大以外,每个订单都有不同的起讫点和不同的时间窗要求。面对大量分散且具有不同起终点和时间窗约束的客户订单,传统的单一运输方式不仅很难同时满足多个客户的需求,而且运输成本居高不下。和单一运输方式相比,多式联运不仅可以同时服务多个运输订单和整合多种运输资源,而且可以通过运输的规模经济效应降低运输成本。多式联运由于具有灵活、可靠和高效的优点而越来越受到运输行业和学术界的重视[2]。
早期关于多式联运路径优化的研究大多是集中于单一订单的路径优化研究。在给定的多式联运网络中,通过不同运输工具的衔接运输,寻找一条将货物从起点运往终点的最短路径。Xiong[3]在给定的多式联运网络中为单个运输订单规划了路径。Liu[4]和Kengpol[5]也对单个运输订单在多式联运网络中的路径优化进行了研究。
当多式联运网络中的订单增多时,路径优化的难度会急剧增加。Chang[6]开发了一种基于拉格朗日松弛技术的启发式算法来求解多个订单在多式联运网络中的路径规划问题。Carlsson[7]研究了以卡车和无人机所组成的多式联运网络的多个运输订单路径优化问题。Ayar[8]也为多订单运输问题构建了混合整数规划模型。以上关于多订单在多式联运网络中运输路径优化的研究都忽略了运输工具的容量限制。Fazayeli[9]和Bevrani[10]在多式联运网络中对多个订单进行路径优化时考虑了运输工具的容量限制。但运输工具可以提供的最大数量并没有限制。目前考虑网络中所提供的运输工具最大数量的研究有Verma[11]和Wang[12]。在对多个运输订单进行运输时,大多是对各个订单分别运输,Moccia[13]和Demir[14]对多个运输订单进行路径优化时,为了实现运输的规模经济效应,允许多个运输订单进行合并运输。
运输订单的时间窗也是多式联运路径优化问题的研究特征。汤银英[15]考虑了多节点时间窗差异的集装箱多式联运路径选择研究。陈钉均[16]研究了有收货时间窗软约束的绿色多式联运路径优化。在刘松[17]和郑红星[18]的研究中,运输订单的时间窗要求也被考虑在内。
在多式联运网络中,所规划的运输订单路径往往是由多种运输方式衔接组成的,当货物的运输从一种运输工具转换成为另一种运输工具时会产生转运成本。现有研究在多式联运网络中对单个订单或者多个订单进行路径优化时都没有考虑运输的转运成本。
虽然目前关于多式联运路径优化的研究既有针对单个订单的,也有针对多个订单的,并且在研究中会考虑运输订单的时间窗和运输工具的容量,但很少研究将运输工具的数量以及运输订单的合并运输同时考虑在内,尤其是将运输订单在多式联运网络中发生转运并将转运成本也考虑在内的研究还没有。
由于各类运输工具的运输能力不同,多式联运物流企业在组织运输的过程中需要考虑所运输的货物容量不能超过所选择运输工具的最大容量。本文研究属于多式联运运作层研究,需要实时决策。在某时刻,多式联运物流企业在网络中可以组织的物流资源数量有限,因此需要将运输资源可以提供的最大数量也考虑在内。基于此,本文以零担多式联运网络为背景,提出了一种考虑订单合并和货物转运的多式联运路径优化问题,给定一组运输订单的起点和终点,本文的研究是以总运输成本最小化为目标,将货物在满足各订单时间窗要求的情况下从各自起点运往各自的终点,给出各个运输订单的运输路径、运输路径上运输工具的衔接方式以及路径上运输工具的使用数量。在研究中,网络中运输工具的容量限制、可以提供的运输工具最大数量限制、运输工具的最晚服务时间限制以及运输的转运成本都被考虑在内。同时,在为运输订单进行路径规划时,为了实现运输的规模经济效应,将多个运输订单进行合并运输。
1 问题描述与模型构建
在1.1部分构建了描述该问题的数学模型。为了简化模型,在1.2部分对模型进行了转化。
1.1 模型构建
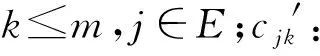
决策变量为:xijk:第i个运输订单选择第j条边上的第k种运输方式,取1;否则取0;yjk:在第j条边上,选择第k种运输方式使用的运输工具的数量;ωiv:如果第i个订单在第v个节点发生转运,取1,否则取0。
模型目标函数可表示为:
(1)
(15)
目标函数是最小化总的运输成本,其中包括三个部分:固定运输成本、可变运输成本和转运成本。约束(2)为容量约束,表示所安排的运输货物数量不能超过在网络中边上所使用运输工具的最大运载能力。约束(3)~(4)和(9)~(10)表示运输订单在运输网络中没有运输回路。约束(5)确保运输网络的连通性。约束(6)表示货物到达时间必须早于所采用的运输方式的服务关闭时间。约束(7)~(8)为订单时间窗约束,运输订单必须在允许的最早出发时间之后从起点出发,并且在允许的最晚到达时间之前到达终点。约束(11)表示对于每个运输订单来说,货物最多只能到达网络中的节点一次。约束(12)表示当运输订单在运输网络中发生运输工具的转换时决策变量xijk与决策变量ωiv之间的关系。约束(13),(14)和(15)表示决策变量xijk、yjk和ωiv的取值范围。
1.2 模型转化
在多式联运网络中各种运输方式的枢纽点分布在城市的不同位置。当货物在城市内发生运输方式转变时,会产生一系列由货物运输、装载和卸载操作带来的转运成本。货物在城市内的枢纽间转运过程描述如图1所示。
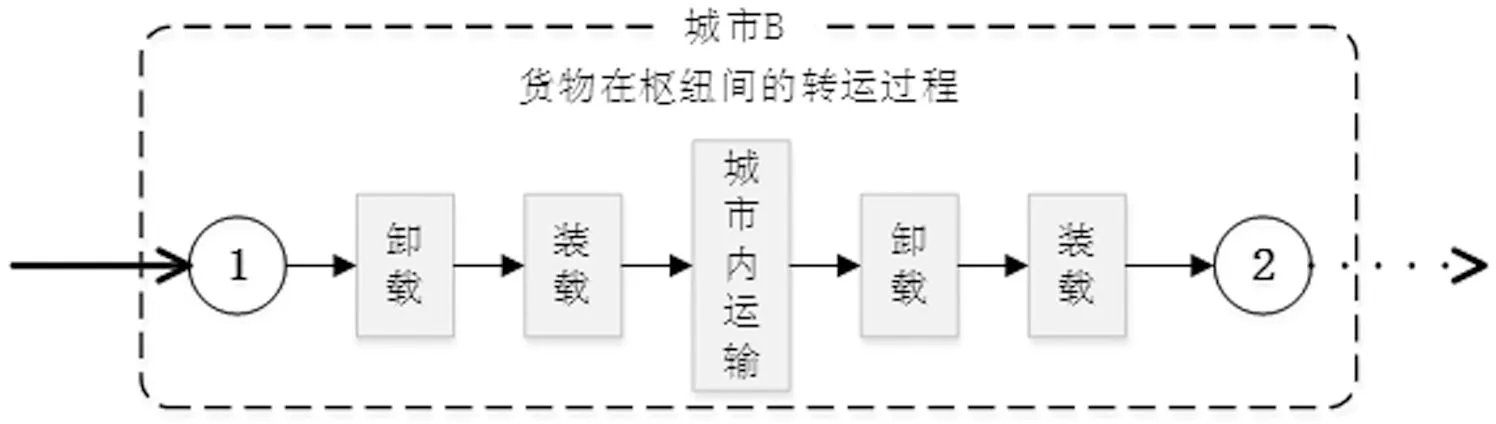
图1 货物在枢纽间的转运过程
货物从城市B的枢纽1运输到城市B的枢纽2的每一种操作的成本都和货物的运输数量相关,为了简化所构建的模型,可将枢纽1到枢纽2的装卸成本折算为城市内的运输成本。那么在城市B内,运输枢纽间的转运成本就转化为了枢纽间路径上的运输成本。
那么在1.1所构建的模型目标函数可以转化为:
(16)
约束为(2)~(11)、(13)和(14)。
通过模型转化,与运输网络中节点选择相关的决策变量转化成了仅和边选择相关的决策变量,降低了计算的难度。转化后的模型仍然属于NP难问题。当问题的规模较小时,可以利用商业软件CPLEX精确求解。当问题规模较大时,精确算法无法求出最优解,此时启发式算法往往能够得出满意的近似解。基于此,本文开发了一种可以快速求出该问题近似最优解的列生成启发式算法。
2 基于列生成的启发式算法
基于列生成的启发式算法框架如图2所示,在2.1为每个运输订单规划一条可行路径,构建初可行列(解);在2.2利用Dantzig-Wolfe分解方法对原混合整数规划问题进行重新建模并生成限制性主问题;子问题的构建和求解在2.3进行分析;在2.4通过变量转换构建原混合整数规划问题的近似最优解。
2.1 初始可行解
为了给每个运输订单规划初始可行路径,开发了一个启发式算法,其详细步骤如下:
Step1松弛原混合整数规划模型的决策变量xijk和yjk为连续变量并求解松弛后的原混合整数规划模型。将所有xijk取值为正的定义为1,剩余xijk取值为非正的都定义为0。

图2 基于列生成的启发式算法框架
Step2在Step1中被定义为0的决策变量xijk集合中,为每一个运输订单规划可行路径。规划可行路径的方法有两种,第一种:在被定义为0的决策变量xijk集合中,为每个运输订单规划一条从起点到终点只经过一个中间节点并且满足容量及时间窗约束的可行路径;第二种:在被定义为0的决策变量xijk集合中,为每个运输订单规划一条从起点到终点只经过两个中间节点并且满足容量及时间窗约束的可行路径。通过以上两种方法,为每个运输订单规划了一条经过一个或两个中间节点的可行路径。然后,将规划出的可行路径对应的决策变量xijk定义为1。
Step3调用CPLEX软件求解小规模的原混合整数规划问题,小规模的原混合整数规划问题与原混合整数规划问题的模型一样,不同之处在于小规模原混合整数规划问题中,将被定义为1以外的决策变量xijk都限制为0。这样,在CPLEX求解的过程中,只需要在决策变量xijk被定义为1的解空间中寻找可行路径。和原混合整数规划问题相比,小规模原混合整数规划问题的求解难度极大降低,CPLEX软件可以快速求出最优解解。
Step4由于小规模原混合整数规划问题的最优解可以为每个运输订单提供可行路径,而每个运输订单的可行路径对应列生成算法主问题的列。为此,输出小规模原混合整数规划问题的最优解并将最优解设置为列生成算法主问题的初始列。
2.2 限制主问题(RMP)
在给定的多式联运网络中,假设对于每个运输订单i,可以枚举出所有的可行路径,定义以下参数和决策变量:
1)参数
令air:表示第i的运输订单被第r条路径服务时等于1,否则等于0,其中i∈R。同样令bjkr:表示第r条可行路径经过了第j条边并使用了第k种运输方式时等于1,否则等于0。那么通过air和bjkr可以定义每一条可行路径(列)。对于一条给定的可行路径,air和bjkr是确定的。令Cr表示第r条可行路径的路径成本。
2)决策变量:
ξr:表示第r条可行路径被使用时为1,否则为0;yjk和原混合整数规划模型含义相同。那么原混合整数规划模型重新定义为:
(17)
式(17)为目标函数,要求总的运输成本之和最小,包括两个部分:路径成本和固定运输成本;式(18)表示每个运输订单都有一个可行的路径;式(19)为容量约束,表示所安排的运输货物数量不能超过在网络中边上所使用运输工具的最大运载能力。式(20)表示决策变量ξr为0-1变量,式(21)表示决策变量yjk为整数变量。把式(20)和(21)表示的约束松弛为(22)和(23),那么得到松弛的线性规划主问题。
0≤ξr≤1,∀r
(22)
0≤yjk≤ncjk,∀j∈E,∀k=1,…,mj
(23)
由于松弛后的主问题的变量数目巨大,选择其中部分变量(至少包含一个可行解)构建一个限制主问题(Restricted Master problem,RMP),即作为列生成算法的限制主问题。
在2.1通过开发的启发式算法为每个运输订单规划了一条可行路径,所有运输订单的可行路径构成了限制主问题的初始列。在初始解的基础上调用CPLEX软件求解该限制主问题。获取相应约束条件的对偶变量值并传递给子问题。
2.3 子问题(SP)
令πi和μjk表示为约束(18)和(19)对应的对偶变量。令ωr表示为路径r所对应的检验数。那么ωr可表示为:
(24)
由于每个运输订单只能选择一条可行路径,那么如果第i个需求选择了第r条路径,则air=1,ap,r=0,其中i≠p。那么式(24)可以表示为:
(25)
对于每条可行路径r,其路径成本Cr又可表示为:
(26)
那么对于路径r的检验数ωr可表示为:
(27)
在列生成算法中,子问题的设计是为了寻找满足每个运输订单运输需求且具有负检验数的“列”(可行路径),那么子问题(SP)可以构建为:
(28)
(38)
式(28)为目标函数,表示最小化检验数。约束(29)~(37)和约束(3)-(11)具有相同的含义。约束(38)表示决策变量bjkr为0-1变量。对于每个运输订单i,子问题以最小化检验数为目标函数,在给定的多式联运网络中为运输订单寻找一条运输成本最小并符合运输订单时间窗要求的可行路径r。子问题是一个最短路径问题,可以利用动态规划算法求解。
2.4 构造近似最优解
在限制主问题和子问题之间不断地迭代的过程中,当子问题无法生成具有负检验数的“列”时,原问题达到最优。通过求解受限制的松弛主问题,得到原混合整数规划问题的下界。此时决策变量ξr和yjk都是连续变量,将决策变量都转换为整数变量并求解此时的限制主问题,可以得到原混合整数规划问题的近似最优解。
3 算例测试及结果分析
3.1部分对算例的生成方法和参数的设置进行描述。算例的测试结果在3.2部分进行分析。
3.1 生成随机算例
根据多式联运网络中节点数量和运输订单数量的不同生成大量不同规模的随机算例。和Fazayeli[9]的研究类似,网络中的节点数量设置为10个和20个,运输订单的数量从10到200个之间变化。根据运输订单数量分为小规模和中等或大规模算例。小规模算例为10或20个节点,订单数量分别为10、20个,每种规模的订单生成20个算例;中等或大规模算例为10或20个节点,订单数量分别为50,、100和200个,每种订单规模生成20个算例,共计200个算例。
在多式联运网络中,存在3种运输方式:公路运输、铁路运输和航空运输。和这三种运输方式对应的运输工具分别是:全货机、卡车和火车。三种运输工具的运输容量分别是15吨,22.4吨和44.8吨,其中火车的运输容量是指一个车皮的容量。三种运输工具的固定运输成本分别是966元、483元和322元,可变成本分别是2.9元/吨·公里、2.1元/吨·公里和1.4元/吨·公里。
由于客户运输订单信息的隐私性,随机生成客户运输订单,运输订单的起点和终点在多式联运网络中随机分布。由于多式联运网络中运输工具的最大容量为44.8,运输订单的运输量在区间[1,44.8]内随机生成。运输订单的最早出发时间在区间[1,24]随机分布。为了每个运输订单的需求都被满足,在多式联运网络中,为每个运输订单都规划一条可行路径。运输订单所要求的最晚到达时间根据所规划的可行路径计算得出。对于在所规划运输订单可行路径上边的运输工具服务关闭时间,设置为运输订单到达该边起点的最晚时间。剩余未在运输订单可行路径上的运输工具服务关闭时间在区间[24,1000]随机生成。对于小规模算例来说,每个边上可提供的某种运输工具的最大数量在区间[5,15]随机生成;对于中等或大规模算例来说,每个边上可提供的某种运输工具的最大数量在区间[10,20]随机生成。
3.2 算例测试结果分析
对于小规模的算例,CPLEX软件可以直接求出精确解,可以利用精确解来评估所开发的列生成启发式算法。小规模算例的求解结果如表1所示。在表1中,“Opt”表示通过CPLEX求解得出的最优解目标函数值,“T1”表示得到最优解所花费的计算时间(单位/秒)。“LB”表示通过列生成启发式算法计算出的原混合整数规划问题的下界,“T2”表示得到下界所花费的计算时间(单位/秒)。“UB” 表示通过列生成启发式算法计算得出的原混合整数规划问题的近似最优解目标函数值,“T3”表示得到近似最优解所花费的计算时间(单位/秒)。“GAP1”表示精确解与列生成启发式算法求解的原混合整数规划问题下界之间的差异。“GAP2”表示列生成启发式算法求解的原混合整数规划问题近似最优解与精确解之间的差异。
在表1中,GAP1的平均值为2.80%,GAP2的平均值为0.28%,通过列生成启发式算法求解得出的原混合整数规划问题下界和近似最优解目标函数值十分接近精确解。这说明对于小规模算例来说,列生成启发式算法可以为原混合整数规划问题提供高质量的下界和近似最优解。T1的平均值为19.25秒,T2的平均值为7.98秒,T3的平均值为8.37。对于小规模算例来说,精确求解需要花费平均19.25秒,而通过列生成启发式算法可以在10秒内为原混合整数规划问题计算出高质量的下界与近似最优解。小规模算例的测试结果表明,所开发的列生成启发式算法性能优越。

表1 小规模算例的求解结果
精确求解随着算例规模的增大,求解时间呈指数形式增长。对于中等或大规模算例来说,大多数算例在短时间内无法求出精确解。那么可以通过列生成启发式算法求解得出的下界来评估启发式算法得出的近似最优解。为此,本文设置7200秒为求解时间阈值,超过设定时间阈值的结算结果不在统计范围之内。表2为中等或大规模算例的计算结果。“GAP3”表示列生成启发式算法求解的原混合整数规划问题近似最优解目标函数值与下界之间的差异。
在表2中,可以看出,在设定的求解时间阈值范围内,中等或大规模算例利用CPLEX精确求解只能求出部分算例。当精确解无法求出时,可以利用所开发的列生成启发式算法求解问题近似最优解。GAP3的平均值为0.64%,表明所开发的列生成启发式算法求出的近似最优解与下界之间差异很小。T2的平均值为211.32秒,T3的平均值为501.87秒。相对于用CPLEX精确求解来说,所开发的列生成启发式算法求解效率较高。
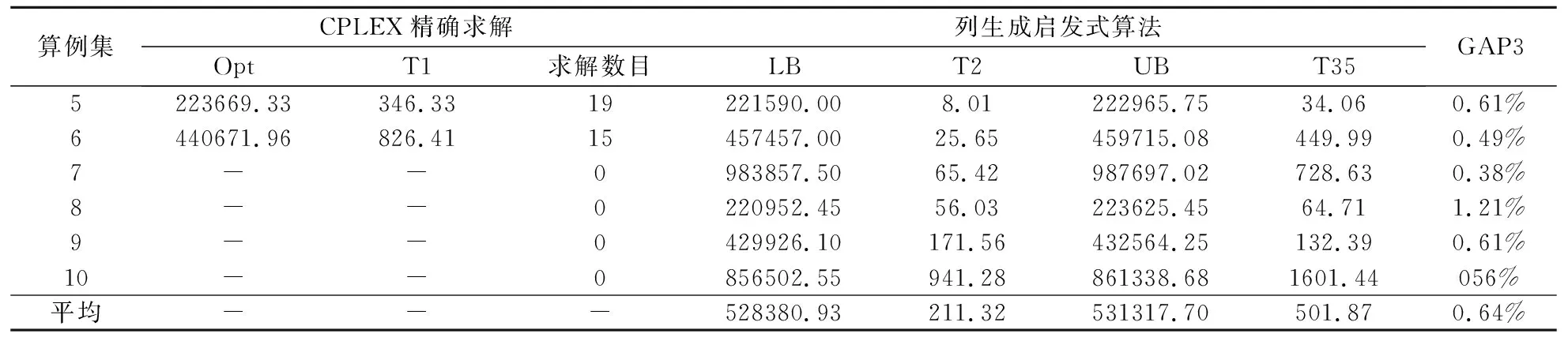
表2 中等或大规模算例计算结果
4 结论
文章提出一种考虑订单合并和货物转运的多式联运路径优化问题,在给定的多式联运网络中,运输工具容量和可提供运输工具的最大数量有限,以总的运输成本(固定运输成本、可变运输成本和转运成本)最小化为目标,将一组具有不同起终点的运输订单,在满足订单时间窗要求的情况下,将货物从各自的起点运往终点。为了获得运输的规模经济效应,将订单进行合并运输。针对该问题,构建了混合整数规划模型并根据问题性质转化模型。为了快速求解模型,开发了一种基于列生成的启发式算法。通过大量算例测试,结果表明所开发的列生成启发式算法在很短的时间内为原混合整数规划模型提供了高质量的近似最优解。对于在某个时刻面对大量运输订单的零担物流企业,该启发式算法能够在较短的时间内为企业提供高质量的近似最优解、提高企业决策效率和节省运输成本。
本文研究仍然有不足之处,研究问题仅以总运输成本为最小化目标。在物流运输过程中,时间也是重要的因素。在未来的研究中,可以考虑以运输成本最小化和运输时间最小化的双目标优化问题。

