雾计算环境下入侵检测模型研究
李晋国,焦旭斌
(上海电力大学计算机科学与技术学院,上海 200000)
0 概述
智能设备的快速发展使得人们迎来物联网时代。物联网应用需要满足移动性支持、地理分布、位置感知和低延迟的需求,云计算很难满足这些需求,因此,雾计算应运而生[1]。雾计算中的雾节点可以执行计算任务,提供低延迟服务。然而,在雾节点中,大多数终端设备都是资源受限的,连接到雾节点的终端可以是智能家电、智能手机、VR 等设备[2]。对于具有此类特征的网络,会遭受拒绝服务(DoS)、中间人(MIM)、恶意网关、隐私泄露、服务操纵等威胁[3]。为了有效地应对雾计算基础设施中的安全威胁,并将相关的损害降到最低,需要加强安全防范,其中,最有效的方法是部署入侵检测系统(IDS)。
目前,雾计算入侵检测系统的实现方法多数基于机器学习[4]和深度学习[5]。文献[6]提出一种基于多层感知机模型且由向量空间表示的轻量级入侵检测系统,其通过使用一个隐藏层和少量的节点,能够在ADFA-LD 中实现94%的准确率、95%的召回率和92%的F1 度量,但是,在ADFA-WD 中上述3 个指标的检测结果均仅为74%。文献[7]提出一种基于Apriori 算法的超图聚类模型,该模型能够有效描述遭受DDoS 威胁的雾节点之间的关联,证明通过DDoS 关联分析可以有效提高系统的资源利用率。但是,该模型仅针对DDoS 这一种攻击方式,不具有泛化能力。文献[8]提出一种基于决策树的入侵检测系统,其分别测试10%数据集和完整数据集,结果表明,该系统不仅能完全检测出4 种大类攻击,而且能检测出22 种小类攻击,但是,该系统只是在NSLKDD 数据集上进行了实验,鲁棒性较差。
相较机器学习,深度学习算法实现了更高水平的检测性能。文献[9]采用类似于客户机-服务器模式的方法来构建模型,在分布式雾节点进行模型训练,该方法的主要缺点是使用基于反向传播随机梯度的技术来更新权重,这需要较长的时间来训练和更新,不适合高度动态的雾计算环境。文献[10]提出一种基于自编码器和孤立森林的深度学习入侵检测方法,在NSL-KDD 基准数据集上进行实验,结果表明,该方法能够达到95.4%的高准确率。虽然该方法利用自编码器完成高维数据的降维,但是训练的自编码器只学习正常流量样本,当遇到攻击样本时,无法对其进行编码,从而造成更高的重构损失,导致模型收敛性变差,无法满足雾计算低时延的要求。
雾计算具有资源受限的特点,这使得在雾节点中无法部署大型的入侵检测模型,而大数据时代的网络攻击大多是高数据量、高维度的,如何在雾节点上有效、准确地检测与发现入侵,是雾计算入侵防御中的首要问题。其次,雾计算具有低时延的特点,这就要求入侵检测模型要具有时效性。最后,雾计算具有高移动性的特点,这就要求部署在雾节点上的入侵检测模型能够适应异构网络环境,具有鲁棒性。本文提出一种基于改进准递归神经网络的入侵检测模型FR-IQRNN,以在分布式雾节点上实现一种新的入侵检测系统,快速准确地检测雾计算环境中的攻击。具体地,将数据预处理后输入稀疏自编码器中进行预训练操作,为了保证降维后的编码向量具有表现力,堆叠多个稀疏自编码器微调模型参数,同时对隐藏层进行批处理化,加快模型的收敛速度。融合QRNN 模型的前向特征和后向特征,引入注意力机制对数据向量组成的序列进行关键特征增强,利用Sigmoid 函数对入侵样本分类。通过上述过程,实现海量高维数据到低维鲁棒性数据的特征重构,降低深度学习网络的时间开销,提高雾节点中入侵检测模型的检测性能。
1 FR-IQRNN 网络异常检测方案
本文提出的FR-IQRNN 入侵检测算法整体架构如图1 所示。训练过程分为4 个阶段:

图1 本文算法总体架构Fig.1 The overall architecture of this algorithm
1)对原始数据集进行预处理,得到一个规范化后的训练集和测试集。
2)将得到的数据集输入到单个稀疏自编码器中进行预训练,然后微调每个稀疏自编码器的参数,最终获取降维后的编码向量。
3)使用改进的IQRNN 模型对降维后的数据进行分类处理,将检测到的攻击行为和原数据作对比,反向更新网络权重,优化网络参数,选取最优效果的模型参数,应用测试数据集进行测试。
4)采用该领域公认的评估指标[11]对本文算法的性能进行评估。
1.1 非线性数据降维
预处理后的数据维数高达196 维,其中多包含一些冗余特征,无论是在计算开销、内存空间还是分类算法的可用性上,都影响着入侵检测效果。传统的自编码器以最小化代价函数为目标,基于反向传播算法迭代优化模型参数,每次训练完成都将隐藏层的输出作为下一层自编码器的输入,直至最后一个隐藏层的输出作为最终的降维特征[12]。由于隐藏层中神经单元的数量小于输入层,因此对高维复杂的网络流量数据起到了降维的作用。
1.1.1 稀疏正则化
为了减少模型参数以降低模型训练难度,同时防止模型过拟合,本文引入稀疏正则化项Jsparse来选择性地激活神经元,这样激活的神经元依赖于数据,有助于使编码数据具有良好的特征从而更易区分。具体地,用常数ρ表示已经激活神经元的比例,平均激活比例为,其中,N为隐藏神经元的数量。KL(Kullback Leibler)散度可以保证接近常数ρ,KL 散度公式如下:

选用常数μ与KL 散度值相乘,可以得到稀疏正则化项Jsparse,如下:
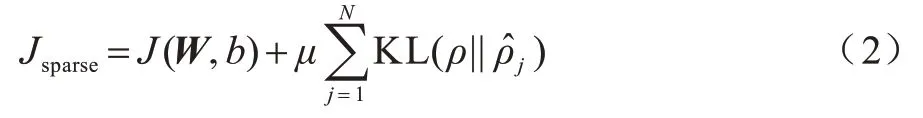
1.1.2 堆叠化处理
经过稀疏正则化的自编码器(SAE)降维能力有限,为了使得最终的特征更小并且有代表性,本文堆叠3 个SAE,并且设置SAE 网络结构的隐藏层数为4,隐藏层神经元数分别为{128,64,32,32}。在前一个SAE 训练完成后,将当前SAE 的输出作为后一个SAE 的输入,逐层训练结束后对堆叠后模型进行微调,改善每层的权重参数。图2 所示为SAE 的堆叠化过程。
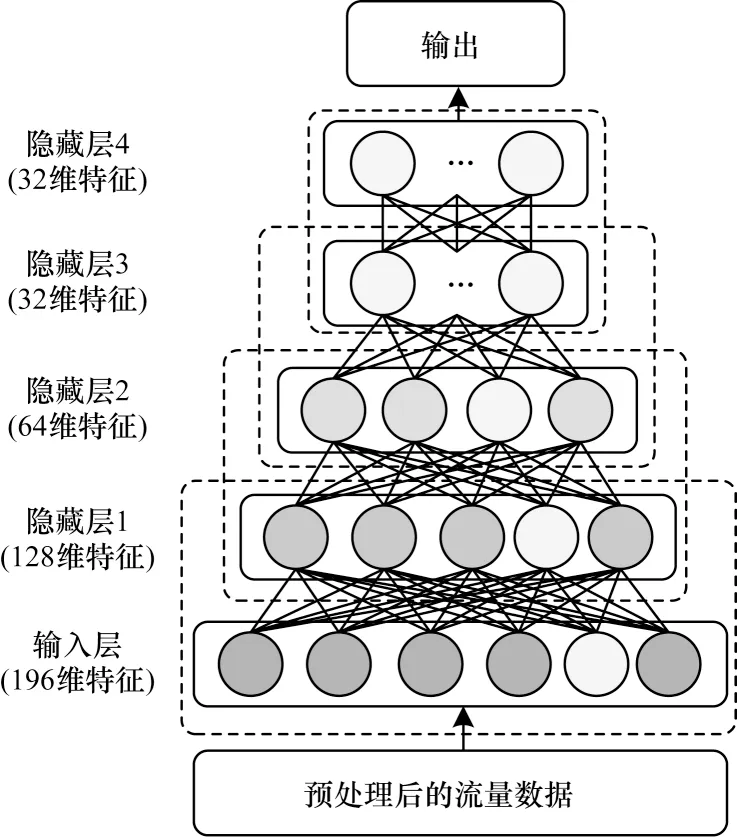
图2 SAE 的堆叠化过程Fig.2 SAE stacking process
SAE 的堆叠化过程包括预训练和微调2 个阶段。预训练是一个无监督的训练过程,即使用大量的无标记流量数据对SAE 进行逐层贪婪学习。预训练阶段的步骤如下:
步骤1将编码后的网络异常流量数据输入到SAE 的可见层中,初始化连接权重W和偏置项b。
步骤2训练第一个隐藏层的网络参数,通过训练参数计算出第一个隐藏层的输出。
步骤3使用无监督学习方法对SAE 进行训练,计算损失函数值Lw,b,不断更新权值W和偏置项b,直到损失函数值达到设定的阈值不再变化。
步骤4将前一网络层的输出作为下一网络层的输入,用同样的方法训练该隐藏层的参数。重复步骤3,直到SAE 所有的隐藏层都被训练完成。
上述预训练过程无法获得输入向量到输出标签的非线性映射,因此,需要在SAE 网络的最后一层添加一个连接层,并使用反向传播方法进行微调。微调阶段的步骤如下:
步骤1将每个SAE 训练的隐藏层连接起来,构建堆叠的SAE,将连接权重W和偏差项b设置为预训练阶段所得到的值。
步骤2在最后一层级联一个Sigmoid 分类器,结合带标签的原始数据训练Sigmoid 分类器的网络参数。
步骤3使用预训练阶段和微调阶段的网络参数作为整个深度网络的初始化参数,找出损失函数最小时的参数值作为最优参数。
步骤4利用反向传播算法对SAE 模型获得的最优参数进行微调。
1.1.3 批量标准化
随着网络的深入,训练过程变得越来越困难,收敛速度也越来越慢。本文采用批量标准化(Batch Normalize,BN)的思想[13]来解决该问题。在微调阶段的第4 步中,存在反向传播过程中底层神经网络梯度消失的现象。BN 是指通过归一化方法,将神经网络每一层中任意神经元的输入值分布强制调整成均值为0、方差为1 的标准正态分布,从而使得非线性变换函数的输入值落在对输入敏感的区域,避免梯度消失的问题。图3 所示为引入BN 的改进SAE 堆叠化过程。

图3 改进的SAE 堆叠化过程Fig.3 Improved SAE stacking process
BN层对隐藏层中各神经元激活值的转换公式如下:

其中:x(k)为该层对应的神经元的线性激活值;Ε[x(k)]是本次训练过程中所有训练实例得到的线性激活值的平均值;Var[x(k)]是线性激活值的方差。假设训练过程中有n个实例,则Ε[x(k)]和Var[x(k)]的计算公式分别为:
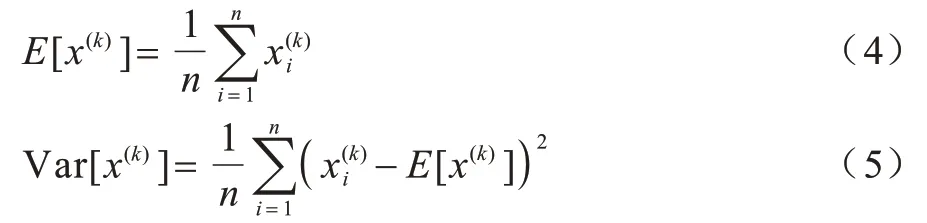
为了防止改变分布后SAE 网络的表达能力下降,在每个神经元上增加调整参数scale 和shift 来激活逆变换操作。逆运算表达式如下:

1.2 改进的QRNN 模型
由于网络入侵流量数据具有高维度以及时间依赖性的特点,因此本文利用QRNN 高度并行化兼具时序性的特点进行时空特征提取,同时加入双向特征融合方案改进QRNN 网络,引入注意力机制对关键特征进行增强,改进的QRNN(IQRNN)模型结构如图4所示。
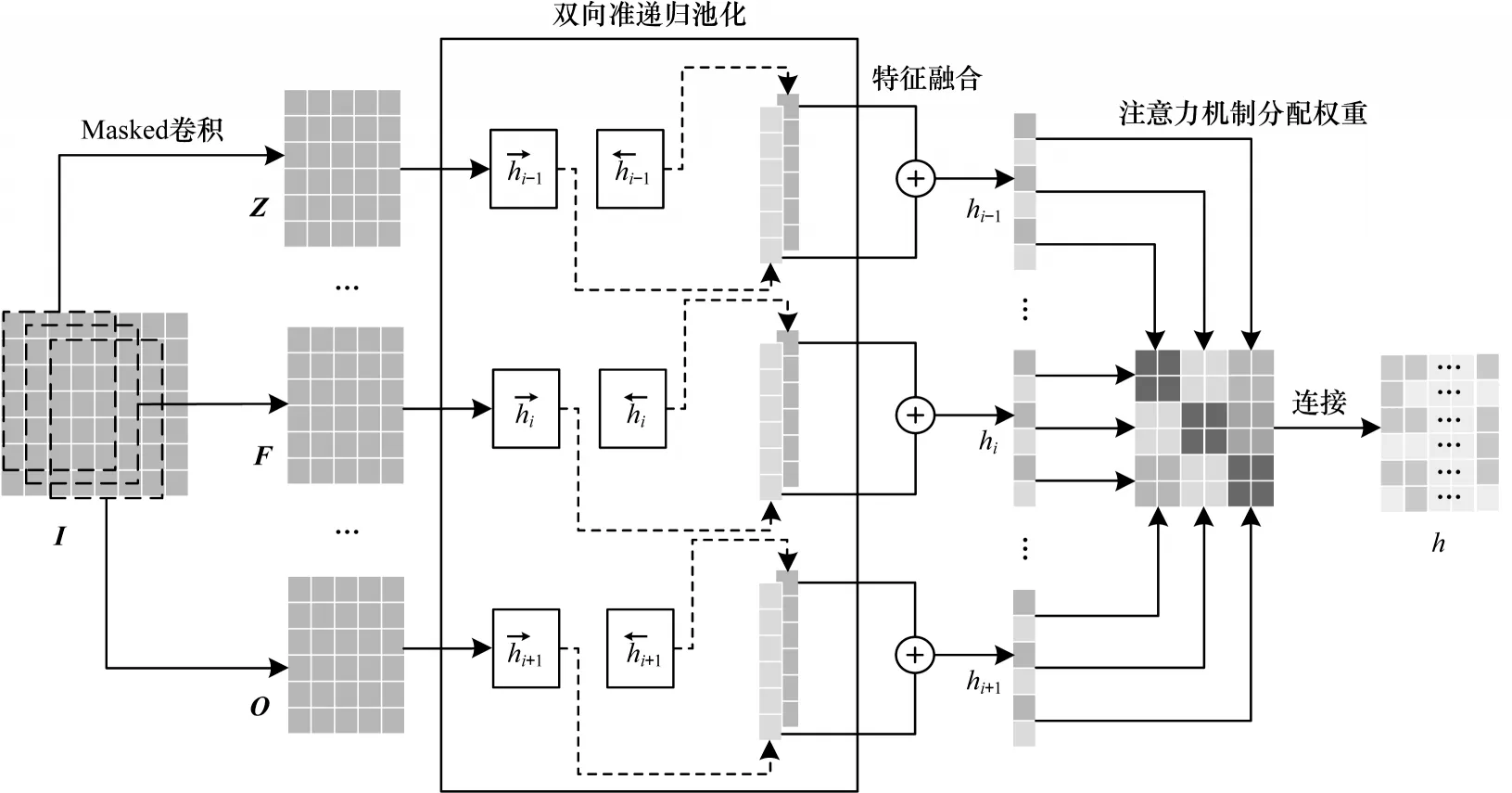
图4 IQRNN 模型结构Fig.4 IQRNN model structure
1.2.1 时空特征提取
QRNN 是长短期记忆(LSTM)网络和卷积神经网络(CNN)的混合神经网络,其结合了两者的优点。与原始LSTM 相比,QRNN 可以在雾节点上高度并行化[14]。与原始CNN 相比,QRNN 可以捕捉流量数据的时序性特征,具有良好的泛化能力。
QRNN 架构如图5所示,阴影部分表示矩阵乘法或卷积,连续方块表示这些计算可以并行运行,白色部分表示沿通道或特征维度并行运行的无参数函数。QRNN的每一层结合2 个类型的层,类似于CNN 中的卷积层和池化层,这2 种类型的层都允许完全并行计算,卷积层支持跨小批量和空间维度的并行化,池化层支持跨小批量和特征维度的并行化[10]。QRNN计算方程如下:
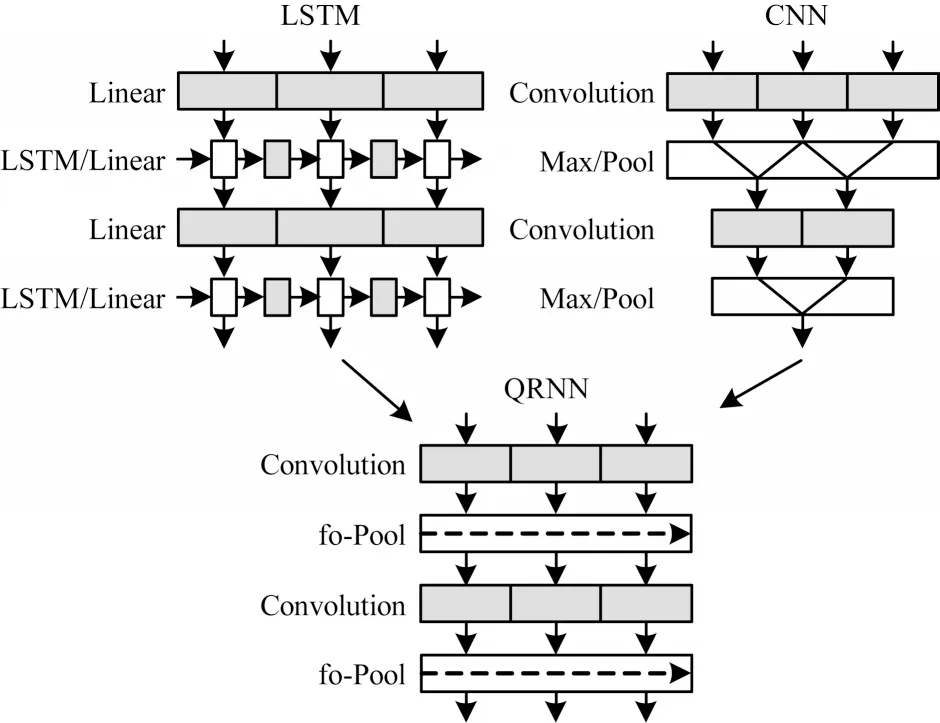
图5 QRNN 结构Fig.5 QRNN structure
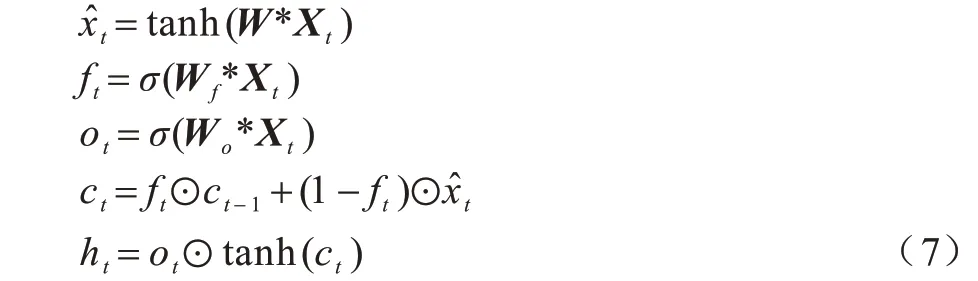
其中:Xt∈Rk×n是输入序列k的n维向量表示;符号*表示沿时间步长维度的掩码卷积;W、Wf、Wο都是Rd×n×k中的卷积滤波器组;k是滤波器的宽度。前3 个表达式是QRNN的卷积部分,这些卷积运算产生m维序列、ft和οt,符号⊙表示元素乘法。最后2 个表达式是QRNN的池化部分,类似于LSTM 单元中熟悉的元素门,不同的是,QRNN 只使用一个遗忘门,即文献[15]中的“动态平均池”。单个QRNN 执行3 个仅依赖于输入序列X的乘向量运算,而不依赖类似于ht-1的先前输出。在已知输入的情况下,这些乘向量运算W*Xt可以在多个时间步中预先计算。因此,不需要在每个时间步加载具有大量内存的权重矩阵。
当执行所需的时间步长增加时,内存的成本降低。因此,这些操作可以在一个矩阵乘法中并行化,如下:
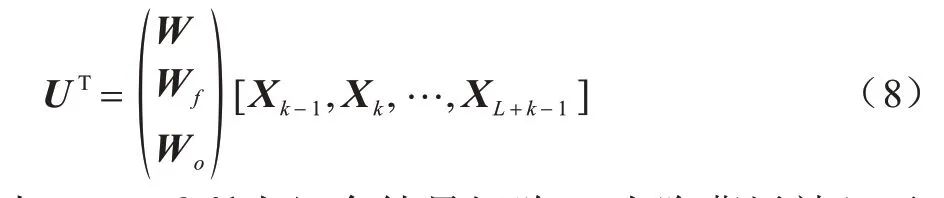
其中:U∈RL×3d为组合结果矩阵;d为隐藏层神经元数;L=T-k+1 为输入序列长度。当使用最小化批处理时,U∈RL×B×3d将成为张量。
1.2.2 双向特征融合
特征融合[16]能显著提升网络性能,因此,被广泛应用于深度学习任务。事实证明,双向特征融合在音素分类[17]、语音识别[18]等领域都明显优于单向网络。尽管特征提取阶段的QRNN 已经提取了前向特征,但是这对于检测背景复杂的网络攻击样本还是不够,因此,本文提出双向特征融合的QRNN 结构,如图6 所示。
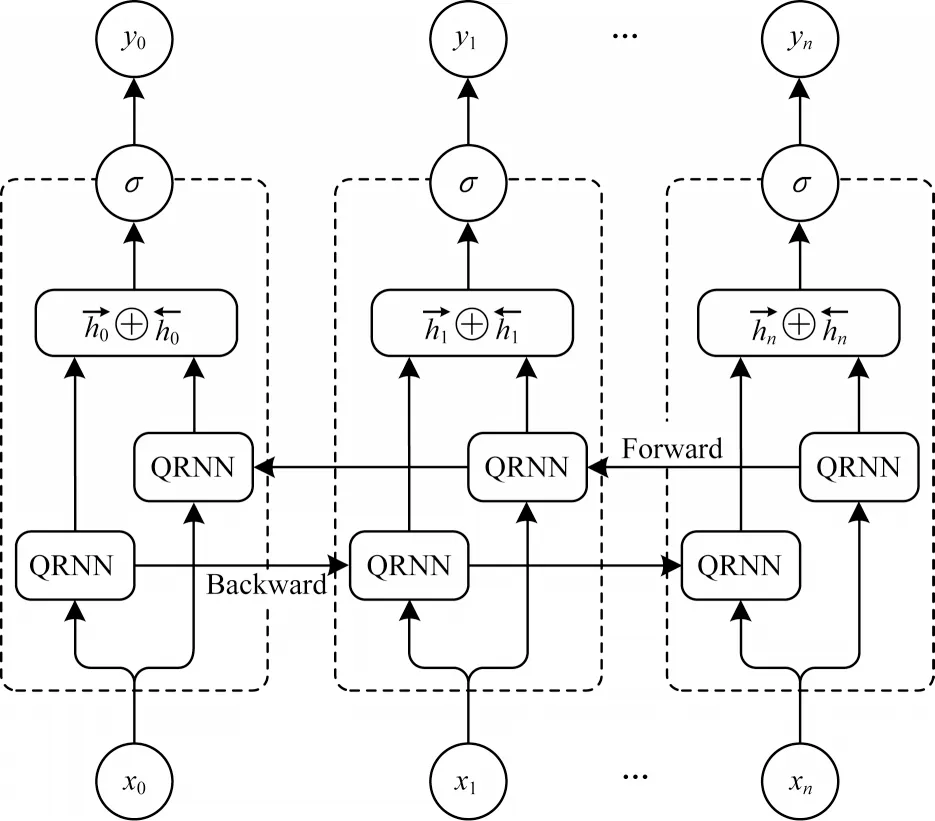
图6 双向特征融合的QRNN 结构Fig.6 QRNN structure of bidirectional feature fusion
在本文所提方案中,输入层负责对特征降维后的数据进行序列编码。前向工作的QRNN单元负责提取输入层数据序列的前向特征,后向工作的QRNN 单元负责提取输入层数据序列的后向特征。输出层用来集成前向和后向工作单元的输出值。具体步骤如下:
1)前向传递。双向QRNN 运行一个时间片1 ≤t≤T的所有输入数据,并确定全部输出值,但是,只对前向状态(从t=1 到t=T)和后向状态(从t=T到t=1)进行正序输入迭代计算,如下所示:

2)后向传递。计算用于前向传递的时间片1 ≤t≤T的目标函数导数部分,但是,只对前向状态(从t=T到t=1)和后向状态(从t=1 到t=T)执行后向传递,公式如下:

1.2.3 关键特征增强
在雾计算入侵检测方案中,引入注意力机制对关键特征进行增强,将提高入侵检测的准确性。注意力机制在图像处理[19]、自然语言处理[20]、目标检测[21]等领域应用广泛,其核心思想是模仿人类观察对象的方式,从大量的信息中选择更关键的部分来实现特征增强。改进后的QRNN 在2 个方面采用注意力机制对流量数据进行分类:一是利用注意力机制来确定哪些维度在分类中起关键作用;二是将QRNN 输出层获得的数据序列添加到注意力机制层,以获得更准确的分类结果。具体步骤如下:
1)计算注意力分布。
设ht是当前目标的隐藏状态值,h是历史隐藏状态值,选用式(12)中的concat 作为score 函数,对注意力权重值at(s)进行计算,如式(13)所示:

计算输入信息中每个元素的匹配度,然后将匹配度得分输入到Sigmoid 函数中,生成注意力分布。
2)根据注意力分布计算输入信息的加权平均值。
将结果输入到Sigmoid 层后,得到注意力权值[α1,α2,…,αN]。利用输入信息对注意力权重向量进行加权平均,计算公式如下:

其中:Wa为注意力机制的权重矩阵,表示需要增强的信息;b为注意力机制的偏差;[x1,x2,…,xN]为注意力机制的输入,即神经网络隐藏层融合后的输出。使用tanh 激活函数对输入向量进行非线性变换,得到的et即为加权计算结果。
雾计算环境需要入侵检测模型具备降维以及检测入侵的能力,本文模型不仅可以实现高维样本的低维映射,而且可以提取有效特征进行攻击检测。FR-IQRNN 算法总体框架如图7 所示。
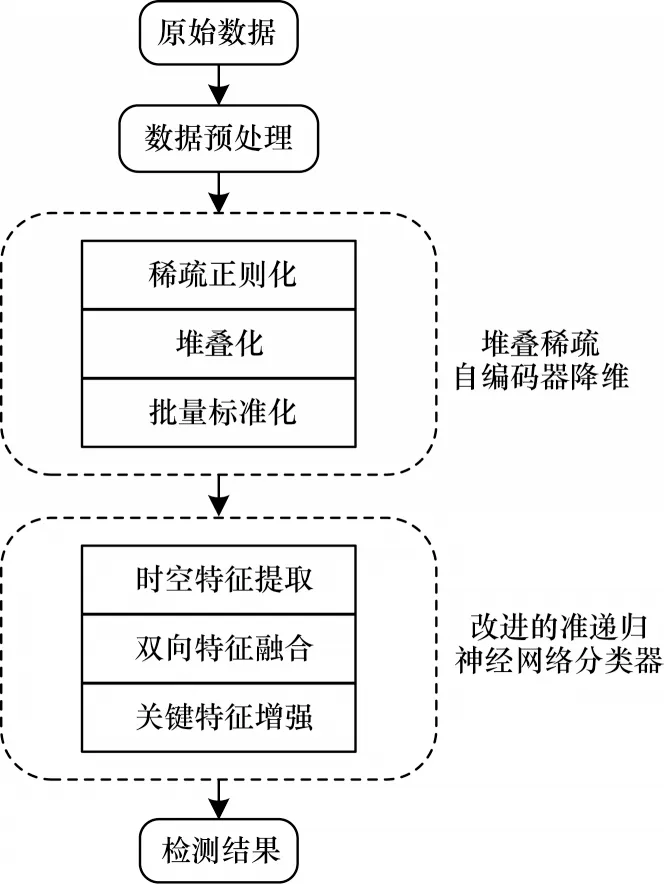
图7 FR-IQRNN 算法流程Fig.7 Procedure of FR-IQRNN algorithm
2 实验结果与分析
2.1 实验环境
为了评估本文入侵检测方案的性能,首先在64 位计算机上采用Python 语言和scikit learn、numpy、pandas、tensorflow-gpu、keras 等机器学 习库进行建模,然后在Intel i7-9750H 2.60 GHz CPU、16 GB RAM、Nvidia Geforce RTX 2080 8 GB GDDR6 GPU 和10.2 CUDA 的环境下进行实验。
2.2 实验数据
本文使用的数据来自网上公共数据集UNSW_NB15,该数据集由澳大利亚网络安全中心实验室提供,记录了实际网络数据中的正常数据流和网络攻击流混合体。数据集的统计信息如表1 所示。

表1 数据集攻击类别统计Table 1 Dataset attack class statistics
UNSW_NB15 数据集存在分布不均的特点,部分攻击类别占比不足十分之一,数据分布的直观表示如图8 所示。
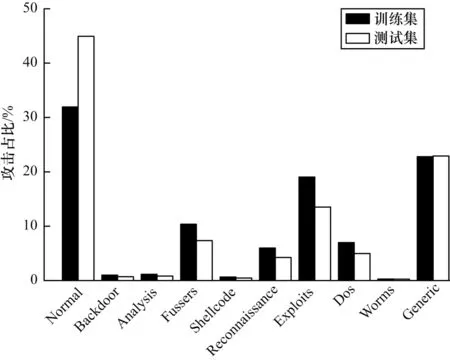
图8 数据集攻击分布Fig.8 Attack distribution of dataset
2.3 数据集预处理
雾节点采集的攻击样本存在多种类型的数据,因此,在网络训练前需对数据进行预处理,将数据类型统一为网络可识别类型,从而便于输入FR-IQRNN 模型并提高训练效果。
2.3.1 数值化
输入流数据中包含多种类型特征,其中一些特征不是数字类型,因此,需要将它们编码为数字类型,以作为神经网络的输入。有2 种编码方式:一种是标签编码器,其将字符型数据中的每一个字符值直接编码为相应的数值大小,缺点是带有数值大小的分类特征会干扰模型学习最佳参数;另一种是one-hot 编码,其将分类变量作为二进制向量表示,每个状态都由独立的寄存器位保存,可以避免数值的干扰。本文选用one-hot 编码器将离散特征转换为连续特 征,特 征“protocol”“service”和“state”这3 个字符型数据将会被编码为数值型数据。例如,“protocol”有“tcp”“udp”和“icmp”这3 种类型的属性,本文将它们依次编码为(1,0,0)、(0,1,0)、(0,0,1),以这种方式将原本42 维特征编码为196 维特征。
2.3.2 归一化
数据归一化可以加快模型求解速度,提高模型的精度,并防止极大特征值影响距离计算。对于最小值与最大值相差很大的特征,如dur、sbytes、dbytes,本文采用MIN-MAX 缩放方法进行缩放,将特征向量映射到某一范围,并根据式(15)对数据进行归一化:

其中:Xi表示每一个数据点;Xmin表示所有数据点中的最小值;Xmax表示所有数据点中的最大值。
2.4 评估指标
异常流量检测的性能评估指标依赖于混淆矩阵,混淆矩阵中值的定义为:
1)真正类(TTP),表示正确分类的异常流量实例。
2)假正类(FFP),表示错误分类的正常流量实例。
3)真反类(TTN),表示正确分类的正常流量实例。
4)假反类(FFN),表示错误分类的异常流量实例。
通过上述4 项生成以下评估指标:
1)准确率(Aaccuracy),表示模型正确分类的样本数与样本总数的比值,计算公式如下:
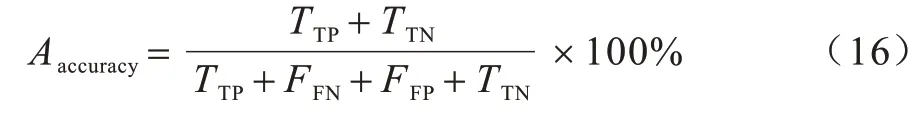
2)精确率(Pprecision),表示模型正确分类的正常样本数与正常样本总数的比值,计算公式如下:

3)召回率(Rrecall,也称查全率),表示模型分类正确的入侵样本数与分类正确的样本总数的比值,计算公式如下:

4)误报率(FFPR),表示被误报为入侵的正常样本数在正常样本总数中所占的比例,计算公式如下:

2.5 模型参数设置
FR-IQRNN 模型需通过设置参数使其达到可控的拟合效果,本文参照传统深度学习的调优方法,为获取一组较优的数据集而进行多次调参实验。模型参数配置如表2 所示。

表2 参数设置Table 2 Parameters setting
UNSW_NB15 数据集中拥有的每条42 维数据特征经预处理后扩展到196 维,在SSAE 模型预训练和微调2 个步骤中,设置预训练的学习率为0.1,损失函数为MSE。经过ReLU 激活函数后,通过微调模型进行优化,设置的微调学习率为0.001,使用0.5 的Dropout 比率对模型参数进行丢弃。在IQRNN 中执行分类操作,迭代次数设置为100 次,采用time step为10 的步数和Adam 优化器,最终得到检测出的样本概率值,用以计算混淆矩阵中的各项指标值。
2.6 结果分析
本文设计4 组实验:
1)将本文入侵检测模型与其他模型的检测性能进行对比。
2)验证本文模型的时间有效性。
3)进行模型调参实验,改用NSL-KDD 数据集检测模型的鲁棒性。
4)进行模型的消融实验。
2.6.1 检测性能比较
为了验证本文入侵检测模型的优势,将其与基于经典机器学习、基于最新深度学习的检测模型在UNSW_NB15 数据集上进行实验,各模型的性能比较结果如表3 所示,其中,包括3 种经典机器学习模型和5 种最新深度学习模型,最优结果加粗表示。从表3 可以看出,与经典机器学习模型和最新深度学习模型相比,本文模型可以达到99.51%的准确率、99.23%的精确率、99.79%的召回率和58%的误报率,其能够更好地检测异常流量。
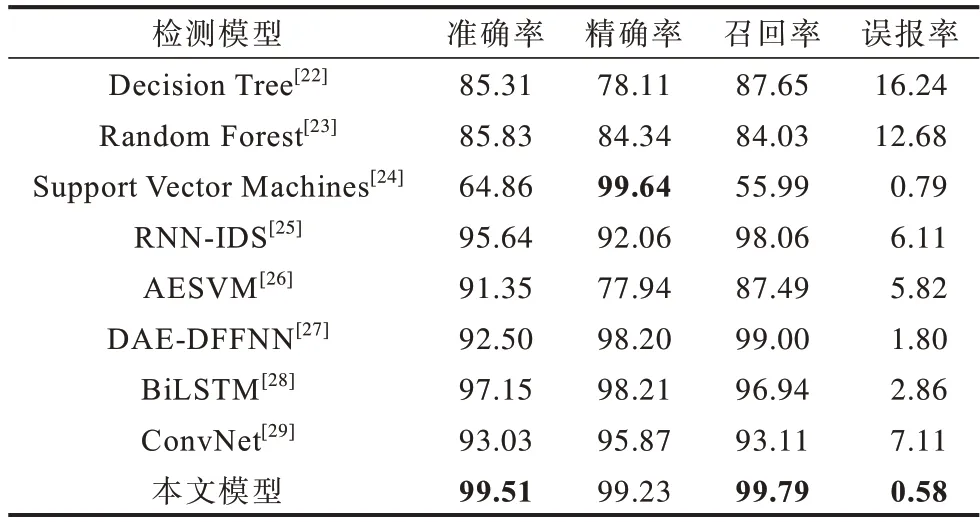
表3 不同模型的检测性能比较Table 3 Comparison of detection performance of different models %
图9 所示为本文FR-IQRNN 模型与2 种基于深度学习的模型在训练精度、测试精度和损失函数收敛情况方面的对比,所有模型都经过了100 次迭代训练,每次迭代之后都进行准确率和损失函数的评估。从图9 可以看出,本文所提模型在训练和测试过程中具有更快的损失收敛速度,能够更早地获得最佳结果,从而提高检测精度。

图9 不同模型的收敛性和准确率比较Fig.9 Comparison of convergence and accuracy of different models
2.6.2 时间性能比较
为了比较本文所提模型和其他模型的计算代价,首先对训练集和测试集分别设置准确率阈值,训练集的准确率阈值设定为0.95,测试集的准确率阈值设定为0.90,然后使用GPU 来加快所有模型的训练速度,最终得到所有模型的训练和测试时间,结果如表4 所示。从表4 可以看出,本文所提模型虽然在每轮迭代上花费的训练时间较多,但用较少的迭代数达到准确率阈值,从而使得总体的训练时间和验证时间最少。考虑到整个系统的运行时间,本文模型可以在雾计算中更快地完成入侵检测,从而延长了雾节点建立防御机制的时间。

表4 不同模型的时间性能比较Table 4 Time performance comparison of different models
2.6.3 方案有效性分析
方案有效性分析具体如下:
1)内部有效性。模型内部有效性是指模型内部参数对模型的影响,具体来说,针对模型的检测精度指标,可以通过调整模型的优化算法和批处理大小(batch size)来改善模型的准确性;针对模型的时间性能指标,可以通过调整time step 的值来提升模型的时间性能。
在深度学习领域,常见的优化算法有SGD、Adam、RMSProp 等,其中,SGD 算法保持单一的学习率更新所有权重,学习率在网络训练过程中不会改变,RMSProp 算法对梯度计算微分平方加权平均数,有利于解决训练过程中上下波动较大的问题,而Adam 算法通过计算梯度的一阶矩估计和二阶矩估计从而为不同的参数设计独立的自适应性学习率。运用这3 种优化算法分别进行模型训练,训练效果如图10 所示,从图10 可以看出,SGD 算法的训练准确率较低,Adam 算法性能相对最优,因此,选择Adam 算法作为本文模型的优化算法。

图10 不同优化算法对准确率的影响Fig.10 Influence of different optimization algorithms on accuracy
batch size 为神经网络经过前向和后向传播操作后的训练样本数,即在每次优化过程中使用多少样本来评估损失。将batch size 分别设置为256、512、1 024,通过准确率来评测最优的batch size。从图11可以看出,随着time step 的提高,模型准确率逐渐上升并达到饱和,相较而言,batch size 为1 024 的模型具有最高的准确率。
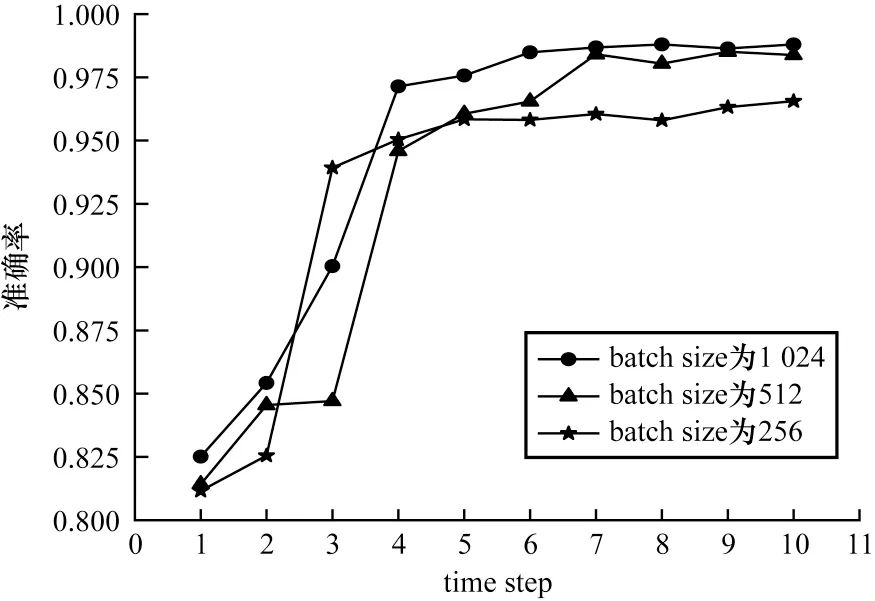
图11 不同batch size 对准确率的影响Fig.11 Influence of different batch size on accuracy
2)外部有效性。外部有效性是指在外部数据驱动情况下模型的健壮性(也称为鲁棒性)。当遭受不同的人为恶意攻击后,雾节点将无法为用户提供正常服务,因此,研究模型的鲁棒性对于雾计算有着重要意义。为了验证本文模型的鲁棒性,使用NSLKDD 数据集进行测试,NSL-KDD 数据集在KDD Cup99 上进行改进,去除了KDD Cup99 数据集中的冗余记录,该数据集也符合雾计算通信环境下流量的基本特征:数据不平衡和多维特征结构。在NSLKDD 数据集中,训练数据集中有125 973 条记录,测试数据集中有22 544 条记录,除了标记为Normal 的数据外,还有DoS、U2R、R2L 和Probe 这4 种攻击类型。NSL-KDD 数据集共有42 个特征(1 个类别特征,7 个离散特征,34 个连续特征)。
在与2.6.1 节相同的环境下,将本文所提模型在NSL-KDD 数据集上进行实验,结果如表5 所示,从表5 可以看出,该模型适用于NSL-KDD 数据集,获得了0.993 9 的准确率和0.004 7 的误报率。与UNSW_NB15 数据集不同,NSL-KDD 中的测试数据集包含许多新的攻击变体,因此,本文模型可以检测出新的攻击变体。

表5 NSL-KDD 数据集上的测试结果Table 5 Test results on NSL-KDD dataset
2.6.4 消融实验
为了验证本文两阶段结合方法的有效性,进行模型消融实验,以验证不同组件对模型的改进效果。依次从FR-IQRNN 中删除每个阶段的组件,包括SSAE、QRNN 双向结构、注意力模块,并将其与完整的FR-IQRNN 进行比较,结果如图12 所示。从图12可以看出:不对数据进行降维导致的分类器检测性能下降最为严重,准确率仅能达到0.919 8,原因是原始数据中包含很多冗余信息,会干扰分类器的特征提取过程,造成最终的性能下降;删除双向结构和注意力机制的模型,最终的检测性能都会降低,这是由于模型无法提取具有关键作用的特征,导致模型识别异常流量出错。
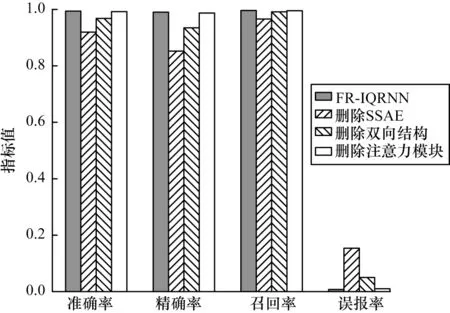
图12 消融实验结果Fig.12 Ablation experimental results
3 结束语
本文对入侵检测问题和深度学习方法进行分析,提出一种入侵检测模型FR-IQRNN。该模型利用堆叠式稀疏自编码器的预训练和微调模式对数据集进行降维,然后结合改进的QRNN 对入侵样本实现分类。实验结果表明,FR-IQRNN 模型能取得0.995 1 的准确率和0.005 8 的误报率,同时具有较低的时间开销,可以很好地解决雾计算环境下入侵检测实时性差、检测精度低的问题。下一步将结合边云协同场景设计分布式入侵检测方案,以提高FR-IQRNN 模型的检测性能。

