新型冠状病毒肺炎疫情影响下中国航空货运量分析与预测*

陈亚东 丁松滨▲ 刘计民 宋晓敏 隋 东

（1.南京航空航天大学民航学院 南京 211106；2.中国民用航空华东地区空中交通管理局 上海 200335）

0 引 言

得益于近十几年来中国经济整体繁荣稳定，航空运输业健康发展，中国航空货运量在2020年新冠疫情以前均保持平稳的增长势头。2020年至今，中国航空货运行业在全球航空市场受新型冠状病毒肺炎疫情（以下简称“新冠疫情”）影响遭受重创难以恢复的背景下实现了“V”形反转，从此前的长期平稳增长转入高速增长，甚至出现“一舱难求”的火爆场景[1]。在其他货运方式供给萎缩，而如新冠疫苗等抗疫物资运输的相关货运需求爆发式增长的条件下，中国航空货运行业遭受新冠疫情的挑战的同时，也得到重大的历史性发展机遇[2]。而在新冠疫情背景下对中国航空货运量的预测能够为中国航空货运企业、航空公司及相关政府管理部门提供整体性与导向性的数据支持，更充分地利用此次历史机遇，助力中国航空货运业高速发展。

在新冠疫情尚未爆发之前，基于时序数据的航空货运量或其他货运量的预测都取得了较好的效果。周叶等[3]使用ARIMA模型基于月度数据对中国航空货运量进行预测，观察到模型对原始数据的拟合效果较好，预测误差较小。文军[4]使用中国航空货运量13年的年度数据，采用马尔可夫链对灰色GM（1，1）模型进行调整，完成了5年的年度航空货运量预测。朱倩等[5]使用聚类算法对数据进行预处理，再使用自适应神经模糊推理系统基于9年的历史数据，得到对未来5年广西地区的航空货运量预测。汤银英等[6]使用Holt-Winters模型对中国铁路月度货运量进行预测，发现其比灰色模型、分组回归等传统预测方法的精确度更高。Liu等[7]研究对比了多种航空货运量的预测方法，认为ARIMA在短期预测中的表现更为优秀。Mancuso等[8]和Blanc等[9]验证了ARIMA和指数平滑模型的组合模型预测精确度优于组成它们的单一模型。在国内国际关于航空货运量的预测研究中，倾向于选择未受群体安全事件（如911事件，H1N1等）影响的数据提取特征，考虑到新冠疫情的影响之深远，目前尚无针对这一影响的成熟的处理方法。

关于正常情况下航空货运量的预测问题已有较多的方法可用，这些方法在特定的时间内也得到了较好的效果，但是在新冠疫情的背景下应用就存在一些问题：①新冠疫情爆发后，中国的航空货运量有过断崖式下跌，许多模型受极端数据影响明显而无法使用；②使用的数据量过少，使用年度数据或较少的月度数据更容易受到突变数据的影响，从而使得预测结果缺乏实用性；③模型的设计复杂，决策者使用不便。

为克服上述问题，将受极端数据影响较小的Holt-Winters乘法模型与ARIMA乘积季节模型作为基础模型，再按最优的赋权方式创建组合模型用作预测。在数据选择时，以2009年1月—2020年12月这144个月度运输量数据为基础（包含新冠受疫情影响的2020年数据），反映疫情对中国航空货运量的影响。同时选取的基础模型都有成熟的统计软件（如SPSS、EViews等）可以使用，故用该组合模型完成对中国2021年和2022年各月的新冠疫情影响下的航空货运量的预测，尝试反映出中国航空货运量在疫情影响下新的趋势。

1 预测模型

1.1 Holt-Winters乘法模型

Holt-Winters乘法模型是1种时间序列分析与预测的模型，它能够处理具有趋势性、季节变化与随机波动的时序数据。它对具有线性趋势、季节波动和受随机因素的影响的时间序列进行分解，对长期趋势、季节变动与数据波动情况分别做出估计，然后建立预测模型，得到预测值[10]。考虑到中国航空货运量具有明显的趋势性与季节性，在2020年以来又有受到新冠疫情影响的短期波动，数据特点与该模型适用条件契合度较高，故选用Holt-Winters乘法模型作为中国航空货运量的组合预测模型之一[11]。

Holt-Winters乘法模型的基本公式[12]见式（1）~（4）。

式中：At为水平因子，是除去季节变化影响的时间序列平均数；Bt为趋势因子，是时间序列的线性变化量；Ct为季节指数；α为数据平滑指数；β为趋势平滑指数；γ为季节改变平滑指数；t为取值时间；m为超前期数；Xt为实际值；Yt+m为预测值；s为季节周期长度，本文数据按月度取值，故s取12。

1.2 ARIMA乘积季节模型

求和自回归移动平均模型（autoregressive integrating moving average，ARIMA）主要用于拟合本身具有平稳性或经过对数转换、开方转换或差分处理后具有平稳性的时间序列。平稳时间序列的性质并不会随着时间的推移而改变，序列的自相关性也不会随着滞后阶数改变[13]。而在处理具有季节性特点的数据时，需要对ARIMA进行复合变换，即采用ARIMA乘积季节模型[14]。

ARIMA乘积季节模型基本结构[15]见式（5）。

1.3 组合预测模型

由于每1种预测方法都有其独特的优缺点，所以将单个预测方法按照特点合理的组合起来，构建组合预测的模型，不仅有利于充分的利用数据的信息，同时能够提高预测模型的精度，减小误差，使预测结果更可靠[16]。本文选用的Holt-Winters乘法模型能较好地凸显时间序列的确定性，ARIMA乘积季节模型能较好地凸显时间序列的随机性，故使用这2种模型进行组合形成优势互补[17]。

式中：Yt为t时间组合预测的结果；fit为参与组合预测的模型i在t时间的值；k为参与组合模型的模型数量；λi为对应模型i的权重。

各模型的权重在组合预测中十分关键，不同的权重会得到不同的预测效果，常用确定各模型权重的4种方法[18]见式（8）~（11）。

式中：Si为模型i的残差；Ni为模型i的方差；Z为目标值；ft为t时间的实际值；l为参与计算的实际值期数。按照上述4种方法来计算出备选的组合预测模型的权重，并通过预测误差的比较来选出4种赋权方式的最优者为组合预测模型的赋权。

2 实例验证

2.1 数据选取与分析

2008年全球金融危机后，中国经济转入中速增长阶段，宏观经济平稳运行，中国航空货运量在这样的背景下稳步提升；2020年1月后，中国航空货运市场受新冠疫情影响出现了大幅下跌。为提取中国航空货运量的长期趋势与疫情冲击，选用2009年1月—2020年12月这144个月的中国航空货运量数据建立模型，对2021年1月—2022年12月的航空货运量进行预测，最后以2021年1月—5月的数据进行预测模型的验证。本文所用中国航空货运量月度数据来自中国民用航空局官网[19]，详细数据见表1，数据对应的时序图见图1。

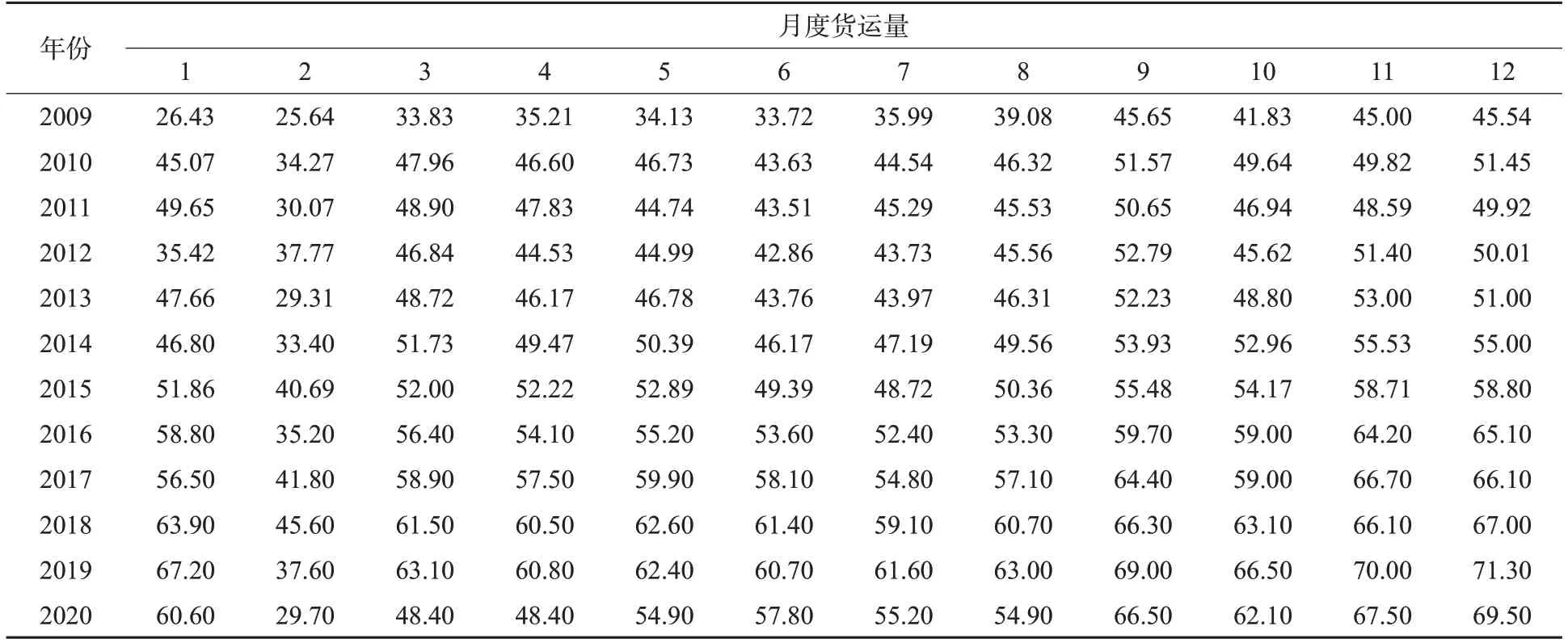
表1 2009—2020年中国航空货运量月度数据Tab.1 Monthly data of Chinese air cargo volume from 2009 to 2020单位：10 000 t

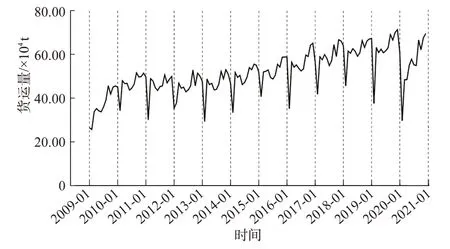
图1 2009—2020年中国航空货运量月度数据时序图Fig.1 Time sequence diagram of monthly data of Chinese air cargo volume from 2009 to 2020

由图1可见：自2009年以来中国航空货运量有明显的上升趋势，同时呈现以年为周期的波动，满足Holt-Winters乘法模型与ARIMA乘积季节模型的基本适用条件。同时，航空货运量各年的数值峰谷与峰顶分别出现在2月与12月，而受新冠疫情影响，2020年2月运输量为10年来次低水平，相较于2019年同期降低21.01%，但是随后快速反弹，保持强劲的上升势头，2020年12月已经恢复到2019年同期水平的97.48%，就月度航空货运量而言，疫情的负面影响在逐渐减小。

2.2 Holt-Winters乘法模型预测结果

通过SPSS25软件的Holt-Winters乘法模块，将中国航空货运量2009年1月—2020年12月的数据代入模型，输出的结果见图2，该模型的检验统计表见表2。

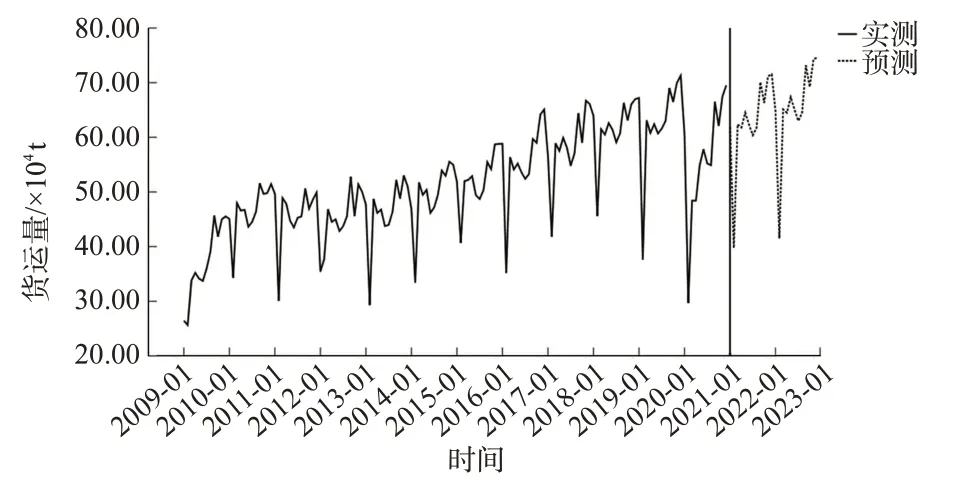
图2 Holt-Winters乘法模型预测结果Fig.2 Prediction results of Holt-Winters multiplication model

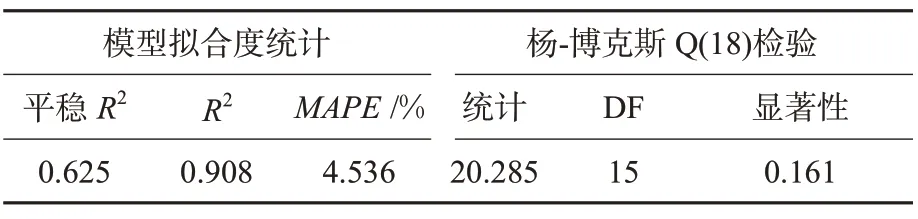
表2 Holt-Winters乘法模型统计Tab.2 Statistical test of Holt-Winters multiplication model

由图2与表2可知：该模型的R2达到0.908，平均绝对百分比误差（mean absolute percentage error,MAPE）为4.536%，模型整体拟合效果良好，误差水平较低。在置信水平为95%的条件下，杨-博克斯Q（18）检验显著性为0.161，大于0.05，即模型残差为白噪声序列，数据特征提取良好。对2021年和2022年的航空货运量预测值见表3。

由表3可知：Holt-Winters乘法模型对2021与2022年的航空货运量航空货运量的预测结果为：2021年12月达到71.54万t，2022年12月达到74.64万t，均高于疫情前2019年12月71.30万t的水平。

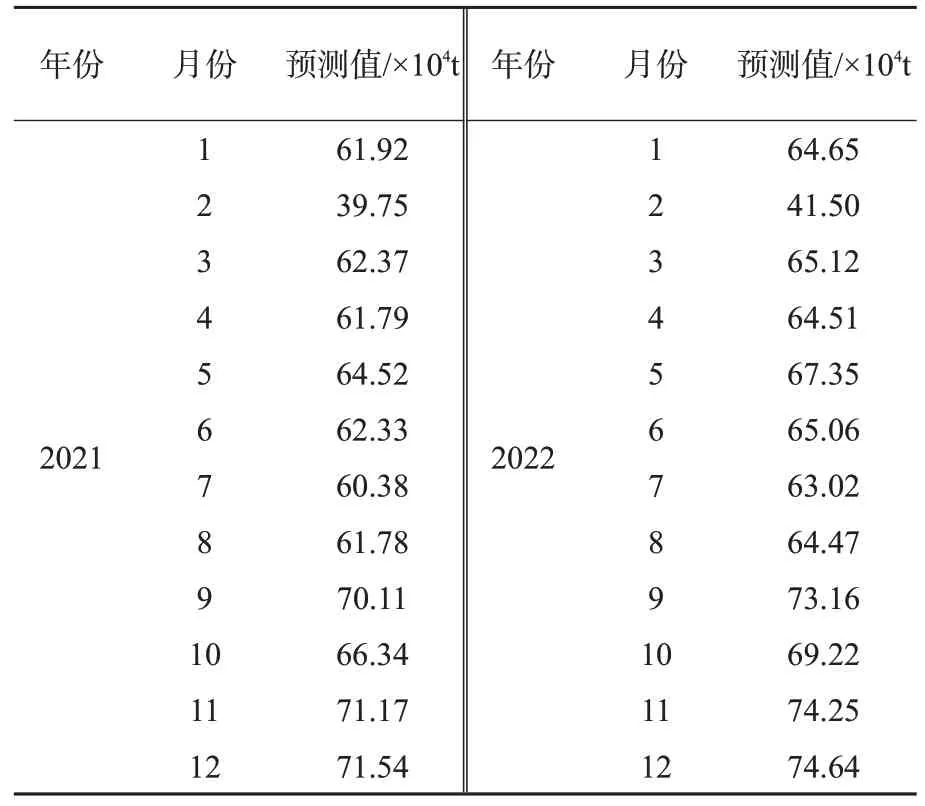
表3 2021年和2022年航空货运量预测值（Holt-Winters乘法模型）Tab.3 Forecasting results of air cargo volume in 2021 and 2022（with Holt-Winters multiplication model）

2.3 ARIMA乘积季节模型定阶与预测结果

由图1可以发现中国航空货运量月度数据具有明显的季节性与趋势性，因此对数据作一、二阶差分与一阶季节差分处理，处理后的结果见图3和图4。

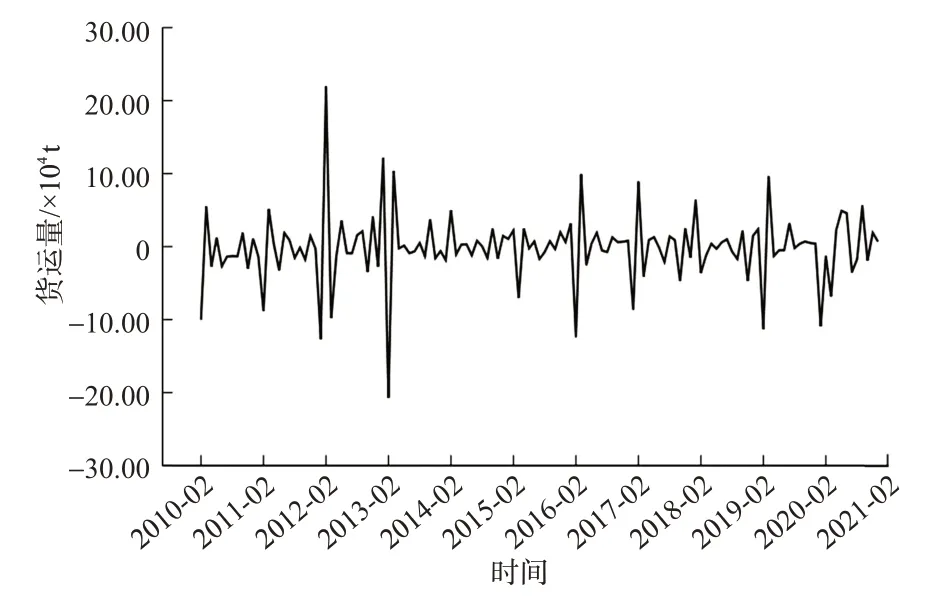
图3 运输量一阶差分、一阶季节差分图Fig.3 1st difference and 1st seasonal difference diagram of transportation volume

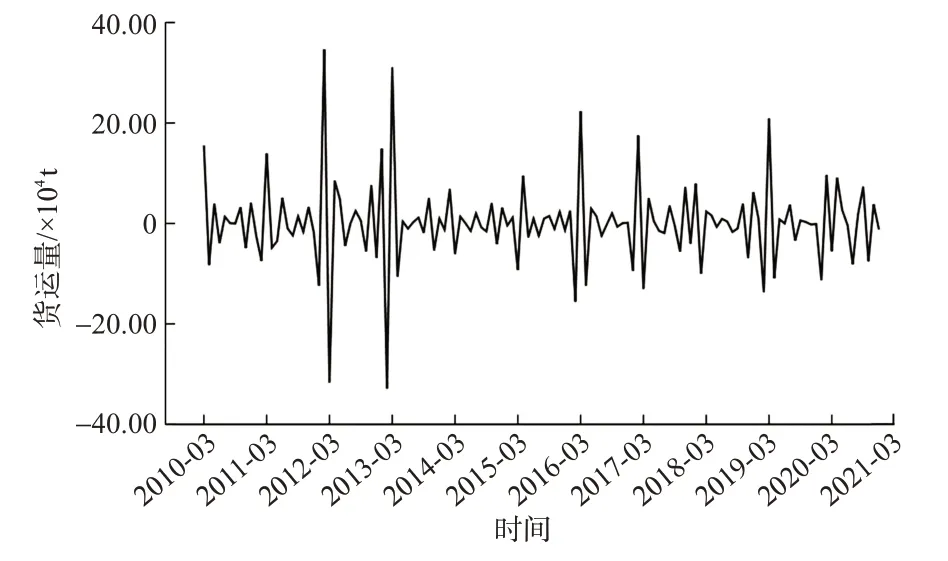
图4 运输量二阶差分、一阶季节差分图Fig.4 2nd difference and 1st seasonal difference diagram of transportation volume

图3与图4显示经过一、二阶差分与一阶季节差分处理后均无明显的线性趋势与季节趋势，但是通过扩展的迪克-富勒（augmented dickey-fuller,ADF）检验发现二阶差分能够通过1%水平的检验，而一阶差分仅能通过5%水平的检验，故选择d=2，D=1。经过二阶差分与一阶季节差分处理后的自相关图与偏自相关图见图5和图6。

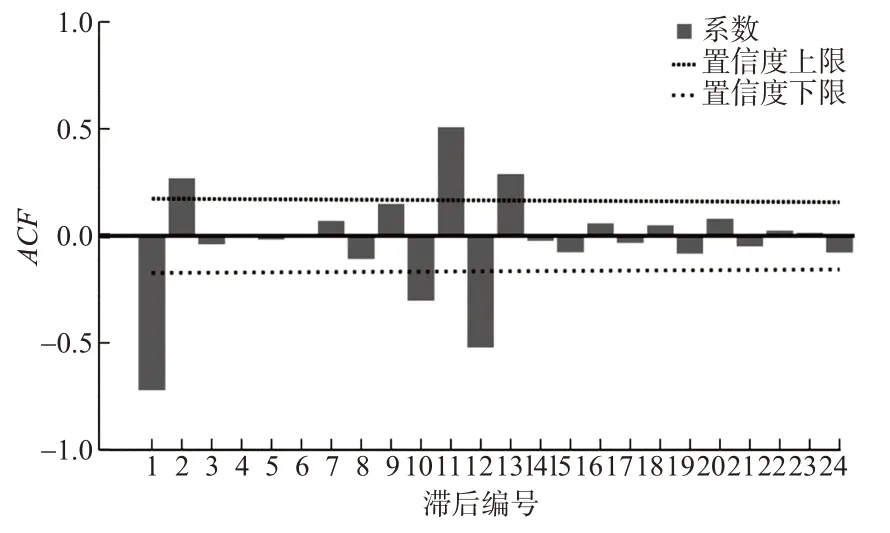
图5 差分处理后自相关图Fig.5 Autocorrelation diagram after data processing

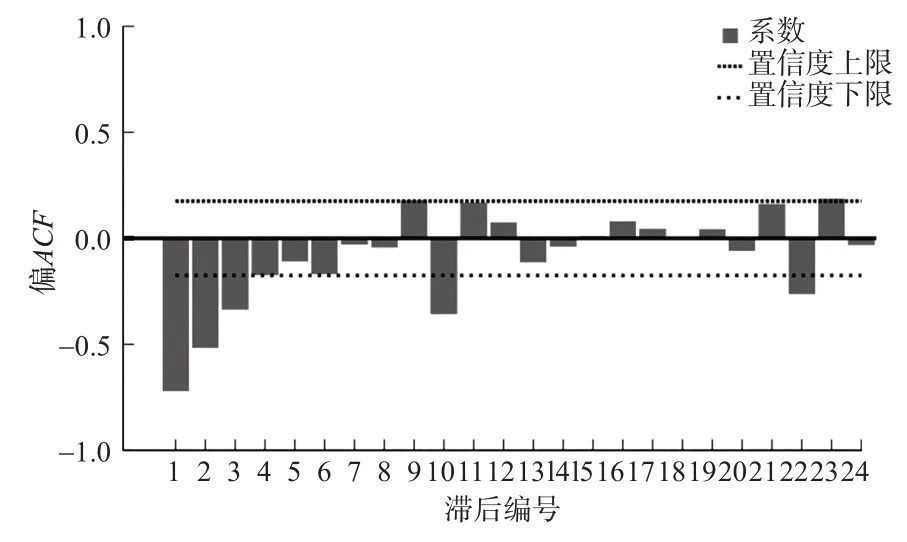
图6 差分处理后偏自相关图Fig.6 Partial autocorrelation diagram after data processing

由图5与图6的拖尾性质判断p和q均大于0，故取备选的（p,q）组合为（1,1），（1,2），（2,1），（2,2）。由于P和Q的取值一般不会大于2[20]，而自回归系数13阶后均在置信区间内，偏自回归系数23阶时仍处于置信区间外，故将P取0或1，Q取2。综上可得共8个备选的不同参数的ARIMA乘积季节模型，使用这些模型对中国航空货运量进行分析，所有模型均能通过杨-博克斯Q（18）检验，各系数组合下的模型检验的结果见表4。

表4 备选模型的检验Tab.4 Verification of alternative models

依据正态化贝叶斯信息准则（bayesian information criterion,BIC），最终从备选模型中选择BIC最小的ARIMA（1,2,2）（0,1,2）12模型作为预测模型，模型预测结果见图7，该模型的检验统计表见表5。

由图7与表5综合分析可知：ARIMA（1，2，2）（0，1，2）12乘积季节模型在处理2009—2020年航空货运量的过程中表现较为优秀，R2达到0.928，平均绝对误差百分比低至3.248%，表明该模型对数据的拟合程度良好。同时在置信水平为95%的条件下，杨-博克斯Q（18）检验显著性为0.676，大于0.05，表明对数据的特征提取充分。运用ARIMA（1,2,2）（0,1,2）12模型对2021与2022年的航空货运量预测结果见表6。

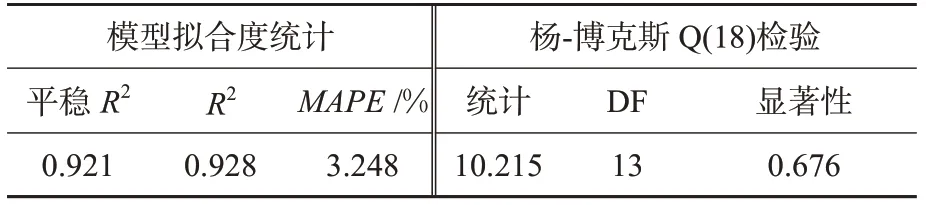
表5 ARIMA（1,2,2）（0,1,2）12模型统计Tab.5 Statistical test of ARIMA（1,2,2）（0,1,2）12 model

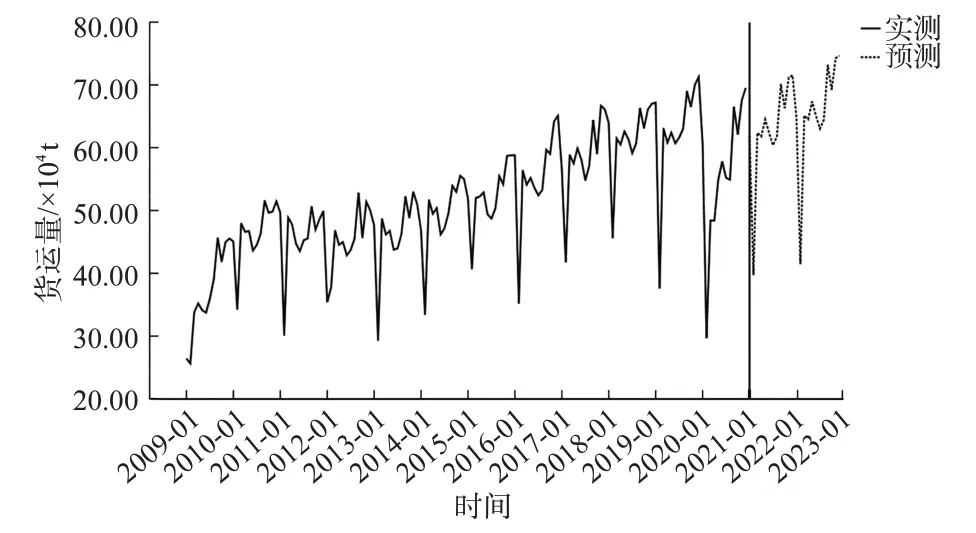
图7 ARIMA(1,2,2)(0,1,2)12模型预测结果Fig.7 Forecasting results of ARIMA(1,2,2)(0,1,2)12model

表6显示ARIMA（1,2,2）（0,1,2）12乘积季节模型对中国2021年和2022年航空货运量的预测更为乐观，认为到2021年12月将达到75.38万t，超过2019年同期水平。同时2022年继续保持良好的波动性上升势头。

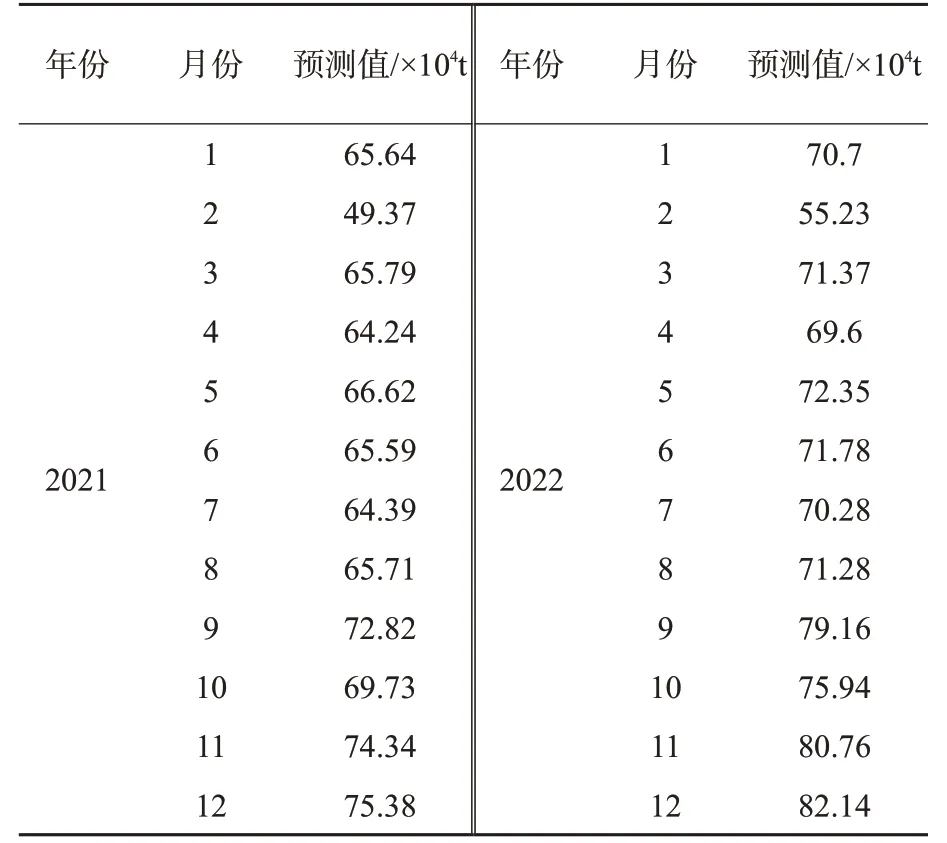
表6 2021年和2022年的航空货运量预测值（ARIMA（1,2,2）（0,1,2）12）Tab.6 Forecasting results of air cargo volume in 2021 and 2022（ARIMA（1,2,2）（0,1,2）12）

2.4 组合预测结果及比较分析

本文采用Holt-Winters乘法模型与ARIMA乘积季节模型建立组合预测的模型，分别根据等权平均法、方差倒数法、残差倒数法及最小二乘法确定4种不同的权重组合，权重分配结果见表7。

表7 组合模型权重分配Tab.7 Weight distribution of combined model

根据中国民用航空局官网数据[19]，2021年1月—5月的中国航空货运量分别为66.90，45.90，65.50，65.50，66.40万t。用Holt-Winters乘法模型、ARIMA（1,2,2）（0,1,2）12乘积季节模型与4个组合模型对2021年1—5月中国航空货运量的预测结果见表8。

表8 各模型预测结果对比Tab.8 Comparison of forecasting results of all models单位：10 000 t

各种预测方法的误差情况见表9。

由表9可知：单一的ARIMA（1,2,2）（0,1,2）12乘积季节模型比Holt-Winters乘法模型在中国航空货运量的预测中预测精度更高。通过对比可以发现：组合模型2，3，4相比于单一的预测模型的预测效果更好，平均绝对百分比误差（MAPE）和最大绝对百分比误差都更小；相比于ARIMA乘积季节模型与Holt-Winters乘法模型，它们的MAPE分别降低了3.70%，13.17%，20.58%与65.69%，69.06%，71.70%；它们的最大绝对百分比误差分别降低了44.18%，46.43%，52.89%与68.51%，69.78%，73.58%，有效的提升了预测的准确性。组合模型4的平均绝对百分比误差为1.93%、最大绝对百分比误差为3.54%，相比于次优的组合模型3，分别降低了8.53%与12.59%，在4种组合预测模型中预测准确度最高，因此选用组合模型4来预测后疫情时代中国航空货运量。

表9 各模型误差比较Tab.9 Comparison of model errors

2.5 中国航空货运量预测结果及分析

2021年以来，中国疫情防控步入常态化阶段，经济稳定发展，伴随着新冠疫苗的大量使用，国际社会对于应对新冠疫情普遍持乐观态度。在假设未来2年国内外的整体经济发展保持稳定并逐渐回到正轨的情况下，使用组合模型4对2021年6月—2022年12月中国航空货运量的预测结果见表10。

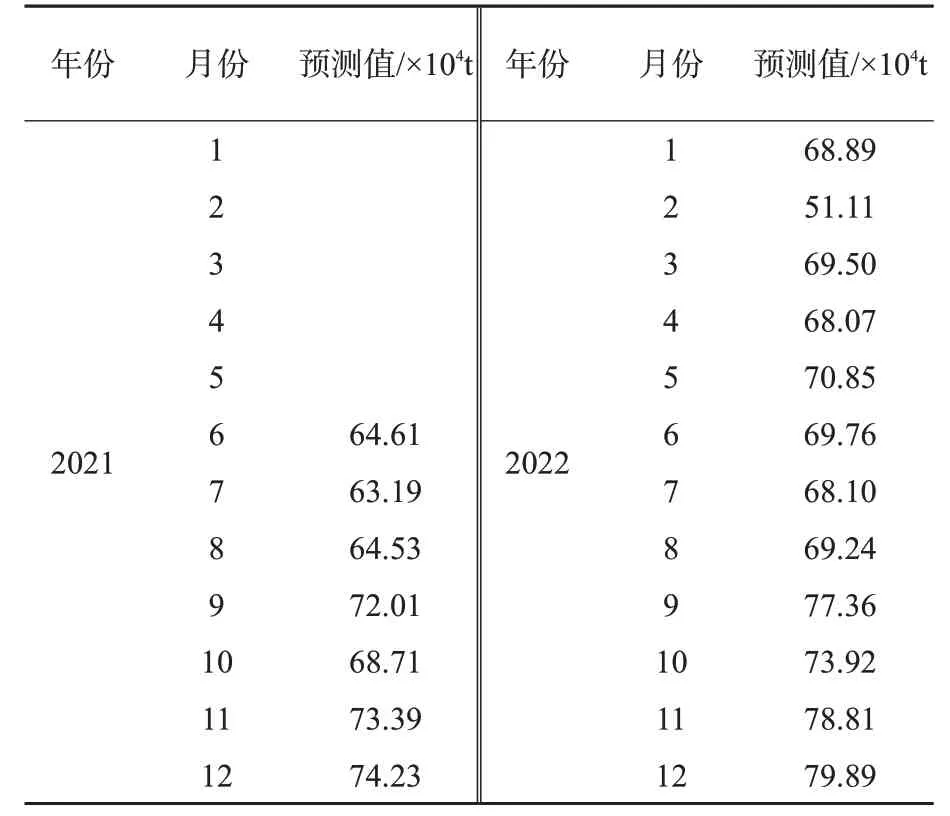
表10 中国航空货运量预测结果（组合模型4）Tab.10 Forecasting results of air cargo volume in China（combined model 4）

组合模型4预测结果表明中国航空货运量会在2021年得到充分恢复，到2021年12月达到74.23万t，相较于新冠疫情前的2019年12月的71.30万t提升4.11%，基本摆脱疫情带来的负面影响，回到健康的增长趋势之中。而2022年各月中国航空货运量在波动中继续保持稳中有升的势头，到2022年底达到79.89万t。

根据中国民用航空局的最新数据[19]，2021年6月—10月的航空货运量分别为64.20万，59.40万，52.00万，59.90万，60.40万t，组合模型4预测结果的误差分别为0.63%，6.38%，24.10%，20.21%，13.76%。组合模型4对1月—6月的预测较为准确，对7月—10月的预测有较大的误差。这是由于7月中下旬开始，国内出现了多处疫情反弹，对航空运输业造成了较大的冲击，而在中国航空货运量统计的细分项也显示主要是由于国内航线的货运量出现了较大幅度的下降导致整体航空货运量的降低。该组合模型所得出的预测结果依赖历史数据，因此国内疫情形势恶化影响了预测的精度。整体来看，在对中国航空货运量的预测过程中，航空货运行业内部稳定运行是预测实施的基础，而外部环境保持稳定是预测结果准确的重要保障。

3 结束语

由Holt-Winters乘法模型与ARIMA（1，2，2）（0，1，2）12乘积季节模型构建的组合模型充分利用了所用中国民航货运量月度数据的时间跨度较大、数据量充分、兼具季节性特征明显的特点，即使在2020年航空货运量受新冠疫情影响而产生剧烈波动的情况下，对中国航空货运量的预测依然取得了较好的预测效果。在几种通过不同赋权方法建立的组合模型中，使用最小二乘法赋权的组合模型（组合模型4）在数据验证时误差最小，预测效果最佳。证明该组合模型在外部环境稳定的情况下可用于对中国航空货运量的短期月度预测。

由于研究使用基础模型只能在较短预测时间内保证预测精度，故该组合预测模型仅能完成对中国航空货运量的短期预测。同时该模型能够准确预测的时长也取决于航空运输业的外部环境稳定性，如当国际政治经济形势或国内疫情防控形势剧烈变化时模型的精度会受到较大影响。为了保证该组合模型的预测效果，接下来的研究中应把更多最新数据纳入模型以提取特征，同时研究采用其他预测方法实现对中国航空货运量的中长期预测。