基于非线性混合充电策略的电动车物流配送路径规划模型*

汪山颖 靳文舟

（华南理工大学土木与交通学院 广州 510630）

0 引 言

近年来，电动汽车（electric vehicles，EVs）由于不排放温室气体、噪声污染小等环境优势，其市场份额迅速增长。2020年中国EVs保有量达492万辆，较2019年增长29.13%。Cazzola等[1]提出物流公司也开始使用EVs提供服务。2018年联邦快递增加1 000辆EVs用于上门服务，2019年美国推出了1个拥有63辆EVs的新车队，中国的京东物流于2018年已将北京的物流车队替换为EVs，因此，电动车路径规划研究对物流运输的重要性与日俱增。

电动车路径规划问题（electric vehicle routing problem，EVRP）是经典VRP的延伸，Qin等[2]归纳出目前针对EVRP问题的主要研究方向有时间窗、能耗方式、充电策略、多车场、异构车队和非线性充电等，许多学者从各个方向提出了不同模型和算法。

在时间窗方面，Schneider等[3]首次提出在经典的EVRP模型基础上计入时间窗约束，设计了1种可变邻域搜索算法（variable neighborhood search，VNS）和禁忌搜索算法（tabu search，TS）的混合启发式算法，并证明设计算法比CPLEX求解器求解速度更快，应用范围更广。在能耗方式方面，蔡银怡[4]提出考虑非线性能量消耗的EVRPTW问题，设计基于变邻域下降搜索改进的混合蛙跳算法进行求解，通过灵敏度分析得出电池容量和载重对配送成本的影响。在充电策略方面，Verma等[5]提出了传统充电和换电2种充电模式，并设计了2步启发式法求解成本最小路径。Keskin等[6]提出允许部分充电的路径规划模型，并设计1种自适应大邻域搜索（adaptive large neighborhood search，ALNS）算法和插入算法求解发现允许部分充电可以改善电动车路由决策。李军等[7]考虑了“间歇补电，浅充浅放”的充电策略，构建了车辆数最小的电动公交调度模型。在异构车队方面，Ugur等[8]利用VNS和可变邻域下降（variable neighborhood descent，VND）的混合启发式算法，解决了多车场、异构车队、多客户访问部分充电的车辆路径问题，其提出的启发式算法在充电、车辆数和配送时间等方面都具有较好的优化效果；Penna等[9]在1组不同行驶里程、容量和固定成本的异构汽车组基础上，提出了1种集合划分模型的迭代局部搜索算法解决带时间窗和充电站的混合车辆路径问题，并通过实例证明了方法的有效性。Macrina等[10]提出1组电动车与燃油车的异构车队的带时间窗的绿色车辆路径问题（green electric vehicle routing problem，GEVRP），设计了1种局部搜索算法优化允许部分充电情况下异构车队的路由，并对污染排放进行了评估。在特殊问题设定方面，揭婉晨等[11]利用改进的分支定价算法验证了大规模数据下需求可拆分车辆路径优化模型的可行性，并发现额定载重比行驶里程对总成本影响更大。Amin等[12]提出利用启发式算法，解决VRP与拣货问题以及时间窗、多车型等附加约束相结合的回收EVs的逆物流路径规划问题，并发现成本项、EVs车辆规模和回收车队会对配送方案的影响。蒋珊珊[13]考虑了路段限行条件下的电动车辆配送模型并设计改进的混合启发式算法对其进行求解，使求解效率和质量均得到提高。在非线性充电方面，早期研究多将电动车充电过程简化为线性过程，与实际误差较大，Montoya等[14]将非线性充电函数引入EVRP，即EVRP-NL问题，构建了1个混合整数规划（mixed integer programming，MIP）模型并使用1种基于迭代局部搜索和集中启发式混合元启发式算法来求解模型。Froger等[15]在Montoya等[14]的研究基础上提出2种新的MIP模型，并提出虚拟CS标记和启发式算法来求解模型。Zuo等[16]在此基础上提出1种新的线性化方法处理带有线性约束的凸型非线性充电函数，列出了MIP模型，比以往的EVRP-NL模型更优越，但并未设计可行的计算方法。王美芹[17]考虑了多种电池折旧方式和充电策略组合模型，利用黄金分割点法线性拟合非线性充电函数，并用CPLEX求解器进行求解，得出各种情况下的路径优化结果。

从发表的论文数来看，EVRP的2个主要扩展研究方向为考虑时间窗和考虑非线性充电函数。在现有的EVs路径问题的研究中，大多数都假设充电时间是充电量的线性函数。而对于非线性充电函数的研究，只考虑了起终点的时间窗约束而不满足每个节点的时间窗需求，非线性充电函数拟合方法复杂，允许充电站无限访问等设定均不符合实际物流配送情况。目前对于多种充电策略的研究比较片面，多为换电和线性快充、完全和部分充电2种，考虑非线性充电特征的多种充电策略的研究还未有涉及，但在实际物流配送中，由于EVs快充满电通常需要1~2 h，换电站的基础设施不成熟且换电成本太高等因素，考虑成本低时间少的充电策略是物流路径规划的必要一步。本研究在已有研究的基础上，根据物流配送的实际情况构建了1种考虑非线性充电、多时间窗、多充电方式的EVRP-NL模型。利用部分估值验证法得出分段函数拟合实际快充过程，并将其线性约束加入EVRP-NL模型，利用Gurobi求解器求解实验算例和实际算例，计算结果表明：混合充电策略可极大缩短EVs在物流配送过程中的充电时长，灵活降低EVs的充电成本，对EVs物流运输的实际应用有重要意义。

1 考虑非线性混合充电的物流配送路径规划模型构建

1.1 问题描述及模型假设

假设配送中心拥有一批车型相同数量充足的电动货车，从配送中心出发，为已知位置和需求的客户提供物流送货服务。货车有载重限制，必须满足客户点的所有需求，单位需求量服务速度恒定。电动货车有里程限制，途中有充电站可进行充电。模型考虑的充电策略为非线性混合充电策略（下文称FCS-NL），即进入充电站后既可选择换电池也可选择充电速率g随充电电量变化而变化的非线性快充方式补充电量。当车辆选择换电池时，单次换电时间和成本固定，换电后恒满电。配送中心和客户点拥有硬时间窗要求，若超过时间窗限制则无法进出配送中心或无法配送。

为了方便模型建立，进一步提出如下假设。

1）配送中心、客户点和充电站位置已知且不变，客户点货物需求已知且不变。

2）客户点和配送货车只能是多对一，而不能是一对多的关系。

3）只考虑配送，不考虑取货，所有货车从配送中心出发并回到配送中心。

4）不考虑充电站货车排队等候，充电无损耗，从配送中心出发时为满电状态。

5）2种充电方式最多只能选择其中1种。

6）货车在节点停留过程中不消耗电能。

7）货车单位行驶成本和行驶速度不变，不考虑电池折旧成本。

根据上述内容，可知考虑非线性充电物流配送路径规划问题的最优路径示意图见图1。EVs从配送中心出发，每条路径都满足物流点的需求量和时间窗条件，若电动车在途中需进行充电操作，则就近选择充电站进行换电或非线性快充，直到访问完所有物流点并返回配送中心。

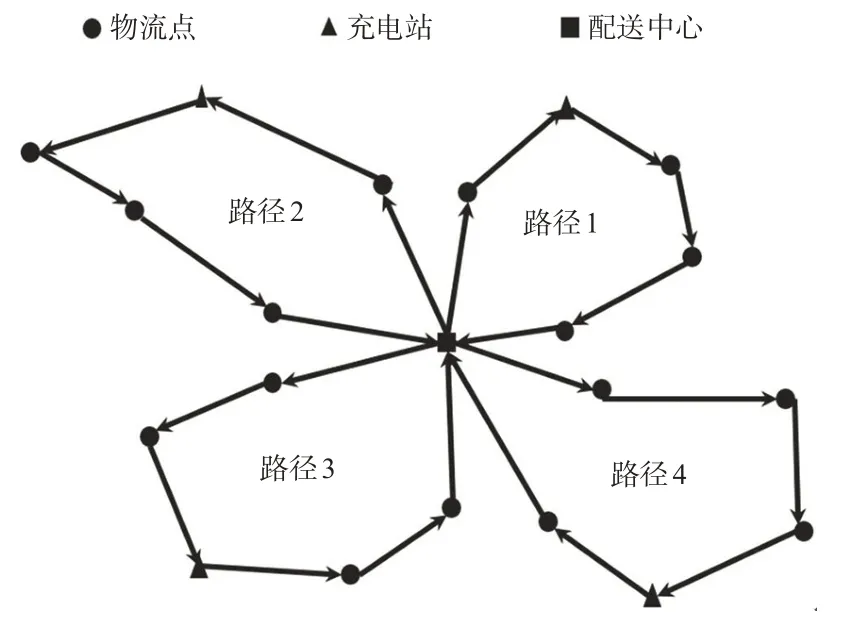
图1 电动车物流配送路径规划示意图Fig.1 Schematic diagram of electric vehicle logistics distribution path planning

1.2 符号说明

路径规划模型所需集合、参数及变量见表1。

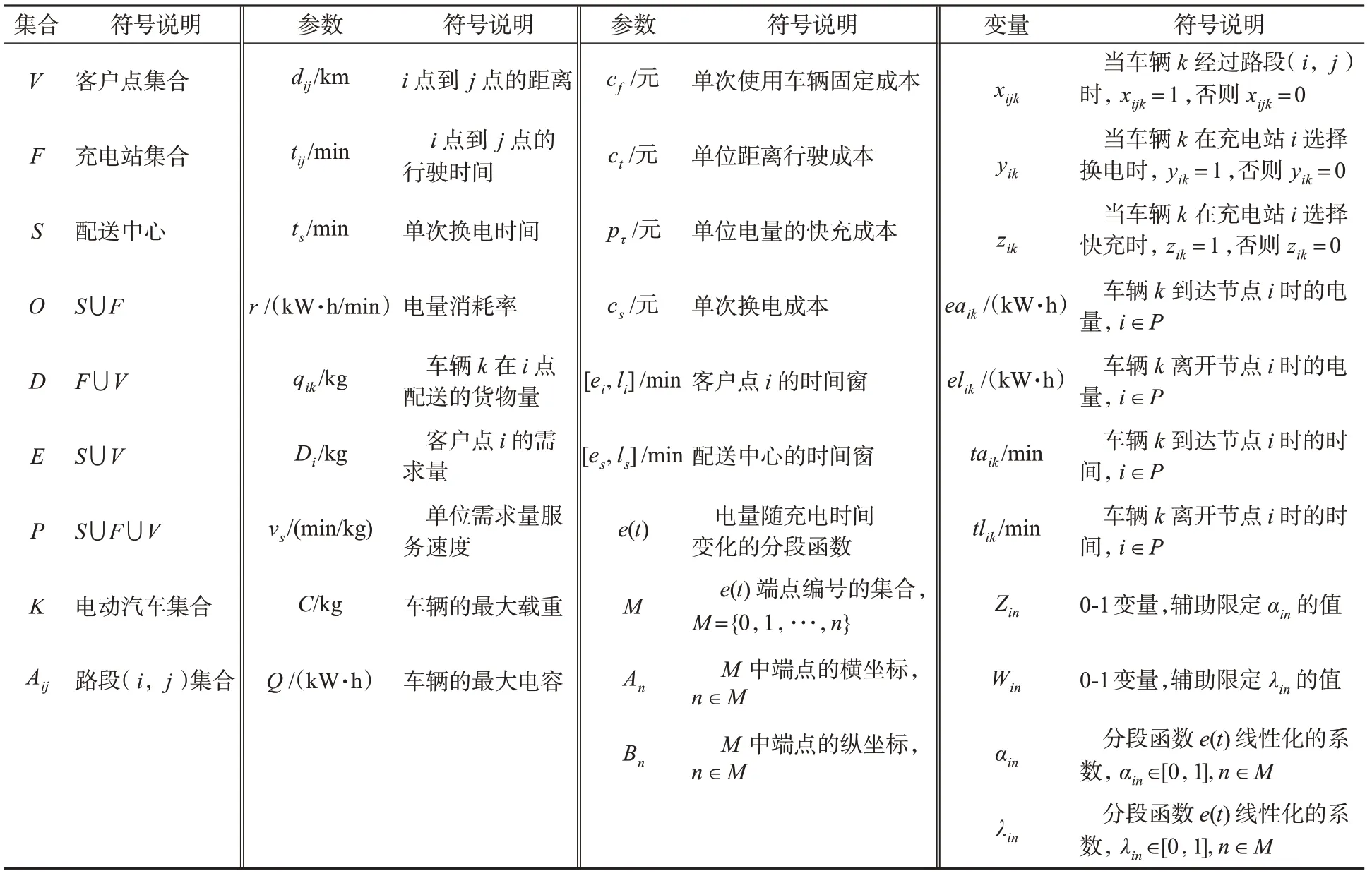
表1 模型符号说明Tab.1 Model symbol description

1.3 非线性充电函数处理

目前我国电动车电池充电过程一般分为2个阶段，示意图见图2。

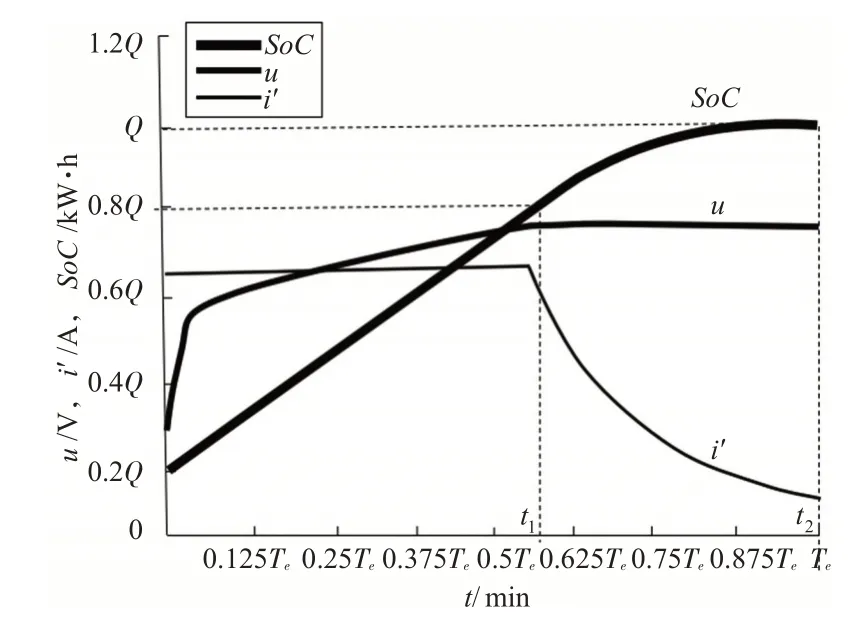
图2 电动车电池充电过程示意图Fig.2 Charging process of electric vehicle battery

图2中SoC为电池电量，t为充电时间，Te为充满电的用时，Q为满电电量。[0,t1]为第一阶段充电时间，此阶段内充电电流一定，充电电压增大，SoC增加速率一定且较快，t1所对应的电量为电池最大电容的80%。[t1,t2]为第二阶段充电时间，此阶段内充电电压达到最大值不再变化，充电电流迅速减小，SoC的增加速率开始降低，此时充电函数变为非线性，t2所对应的电量为电池最大电容。

通过图2虽然可以知道充电函数的走向，但因为充电过程受电流、电压、自恢复以及温度等多因素的影响，用1个确定的表达式来完整拟合却是很困难的[9]。目前经常使用的有3种非线性充电函数拟合方法：①将g设为线性充电时的充电速率，且恒定不变；②将g设为满充的坐标点和零点连接线的斜率，且恒定不变；③使用割线拟合非线性充电函数，近似为多阶段充电。

按照拟合方法①和②[18]得出的充电时间与实际充电时间相差较大；拟合方法③[16]无法直观体现电池充电过程特性，且往往需要引入多个参数，后续计算复杂。

Montoya等[14]为避免处理二维函数，使用Zundorf提出的转换函数法得出充电量与充电时间的函数关系，其中e(t)的原始函数由逼近于Q的凹函数拟合得到。设充满电的用时为Te，利用Python提取Montoya文中22 kW充电功率下各分段充电函数的端点坐标可以得出，电量充至83.99%Q用时59.9%Te；电量充至94.41%Q用时73.06%Te；电量充至100%Q用时100%Te[14]。本研究为避免复杂的原始函数的近似处理，采用部分估值验证法，即预设第一阶段线性充电速率g为1 kW·h/min，其余2段的充电速率由Montoya文中充电速率的比例计算得出，则可列出分段函数e(t)对非线性充电函数进行拟合，见式（1）。

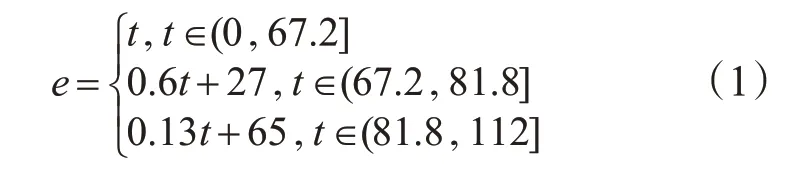
式中：e为电量，kW·h；t为充电时间，min。

根据式（1）可得出拟合后的充电函数图像见图3，可以看出充电速率逐段降低，符合图2中实际充电过程特点。取Q=80 kW·h，g=1 kW·h/min可算出式（1）的Te=112 min且第一阶段充电时间为67.2 min。根据实际可知60≤Te≤120 min，因此Te=112 min符合实际，且Montoya所得分段函数算出第一阶段充电时间为67.09 min，与本方法结果仅相差0.2%，可知估值验证法所得的充电函数符合实际。

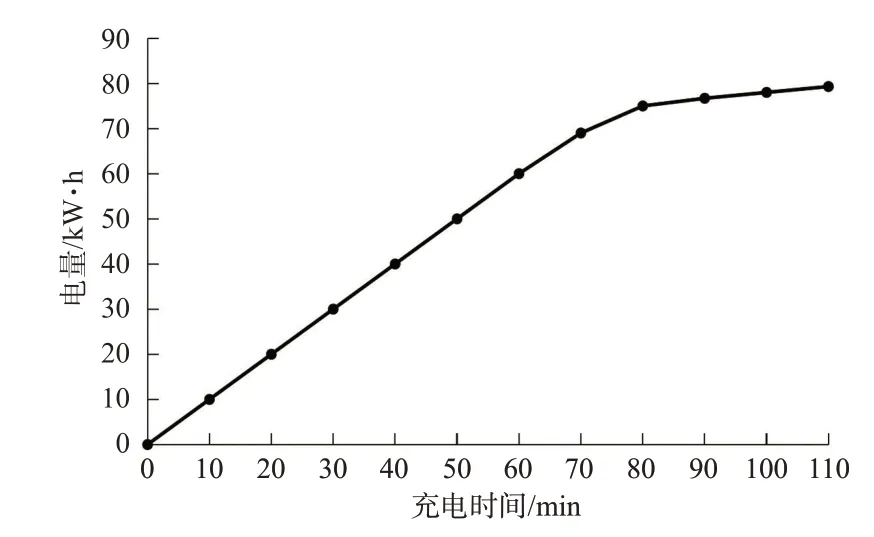
图3 分段函数拟合充电函数Fig.3 Fitting charging function with piecewise function

在数学模型中，需要线性化目标函数中与充电量有关的非线性成本项，本研究利用部分估值验证法，结合Montoya的3段充电速率构造出1个由4个端点3条线段组成的分段函数e(t)来拟合复杂的充电过程。部分估值验证法误差小，操作简便，计算简单，能直观表现出实际过程中充电量与充电时间的变化关系，比Montoya的函数转换法更加简便，比割线法、黄金分割点法等拟合方法得到的分段数更少。

得到分段函数e(t)后需要对其进行线性化处理后加入模型。为了区别充电时长和充电时刻，将式（1）根据车辆达到和离开的充电情况分为2个函数，即分别将taik和tlik带入式（1），将分段函数e(t)线性化，其中i∊F，这里只将到达时刻的分段函数做示例计算。

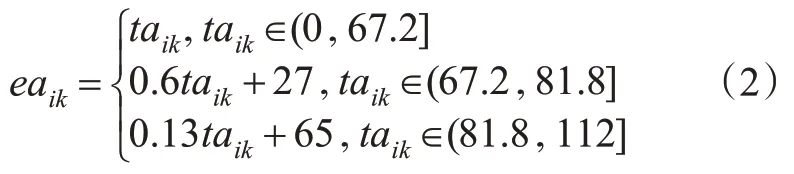
引入连续变量αin和0-1变量Zin，对式（2）进行线性化转换。线性化步骤如下。

1）通过分段点横坐标构建新的自变量。

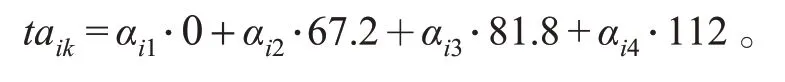
2）通过函数关系求解新的因变量。

其中，αi1≤Zi1，αi2≤Zi1+Zi2，αi3≤Zi2+Zi3，αi4≤Zi3，且αi1+αi2+αi3+αi4=Zi1+Zi2+Zi3=1。

3）推而广之，若分段函数f(taik)有n个端点，各端点的横坐标为A1≤A2≤…≤An，各端点的纵坐标为B1≤B2≤…≤Bn，引入变量αin和Zin可将taik和eaik线性表示为

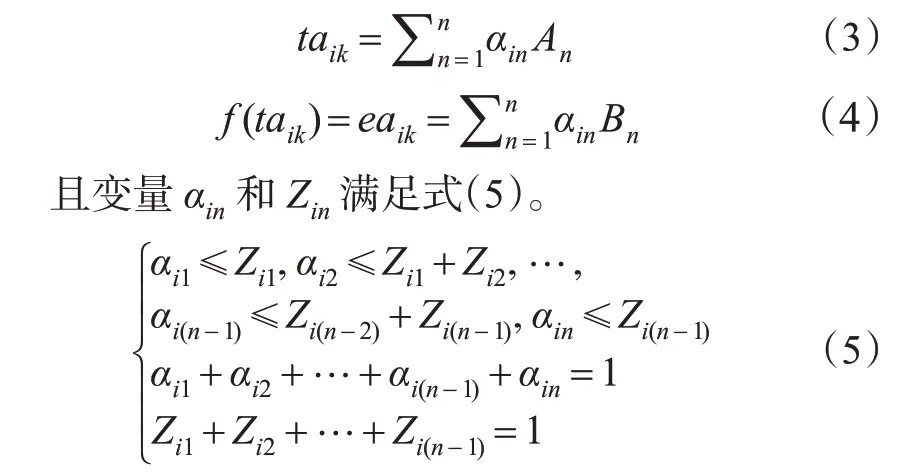
同样的，车辆离开时刻的分段函数可引入连续变量λin和0-1变量Win实现线性化转换，线性表示为

4）线性化结束。

1.4 配送优化模型构建

本研究的考虑FCS-NL的EVRP模型。目标函数的4项成本分别为车辆的固定成本、行驶成本、换电成本和快充成本。目标函数见式（9）。

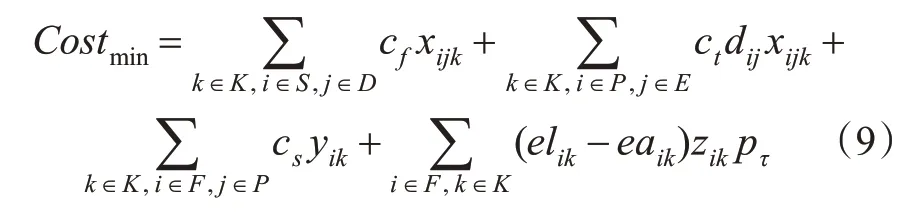
考虑载重、硬时间窗和电量约束的物流配送路径规划模型如下。

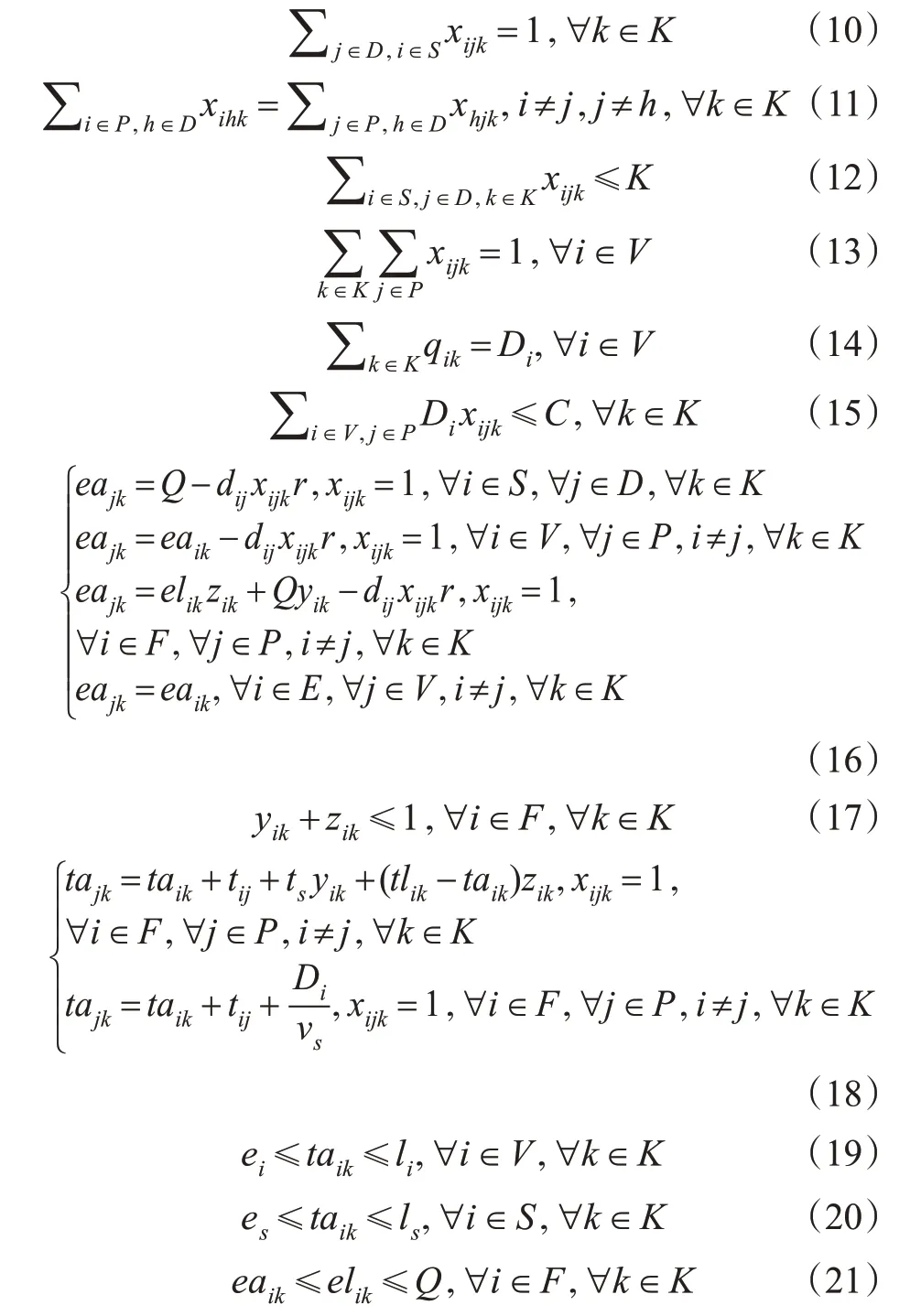
式（10）表示车辆驶出配送中心，式（11）表示流平衡，式（12）表示使用的车辆数不超过车辆总数，式（13）表示每个客户点都被服务，且只服务1次，式（14）表示客户需求都被满足，式（15）表示保证不违反车辆的载重约束，式（16）表示在节点不消耗电量且保证相邻节点的电量消耗的大小关系，式（17）表示车辆在充电站最多只能选择1种充电方式，式（18）保证相邻节点时间的大小关系，与式（18）共同去回路并限制充电站无限次充电，式（19）~（20）表示所有节点不违反硬时间窗，式（21）表示保证充电后不超过最大电量，且物流车可直接通过充电站。

为了在数学模型中用e(t)来近似表达eaik的函数值，需要引入线性约束条件，见式（3）~（8）。其中M={0,1,…,n}，n=4表示e(t)端点编号的集合。（An，Bn）表示e(t)第n个端点的坐标，n∊M。Zin和Win为0-1变量，当Zin=1时，表示到达充电站时，eaik对应在e(t)上的横坐标An-1和An之间，taik对应在e(t)上的纵坐标Bn-1和Bn之间，否则Zin=0；当Win=1时，表示离开充电站时，elik对应在e(t)上的横坐标An-1和An之间，tlik对应在e(t)上的纵坐标Bn-1和Bn之间，否则Win=0，其中i∊F，n∊M{0},k∊K。αin,λin是2组[0，1]内的随机常数，分别表示（eaik,taik）和（elik,tlik）在e(t)的n+1个端点上时，每个端点坐标前的系数，且系数之和恒为1。因此，拟合分段充电函数的线性化约束可表示如下。

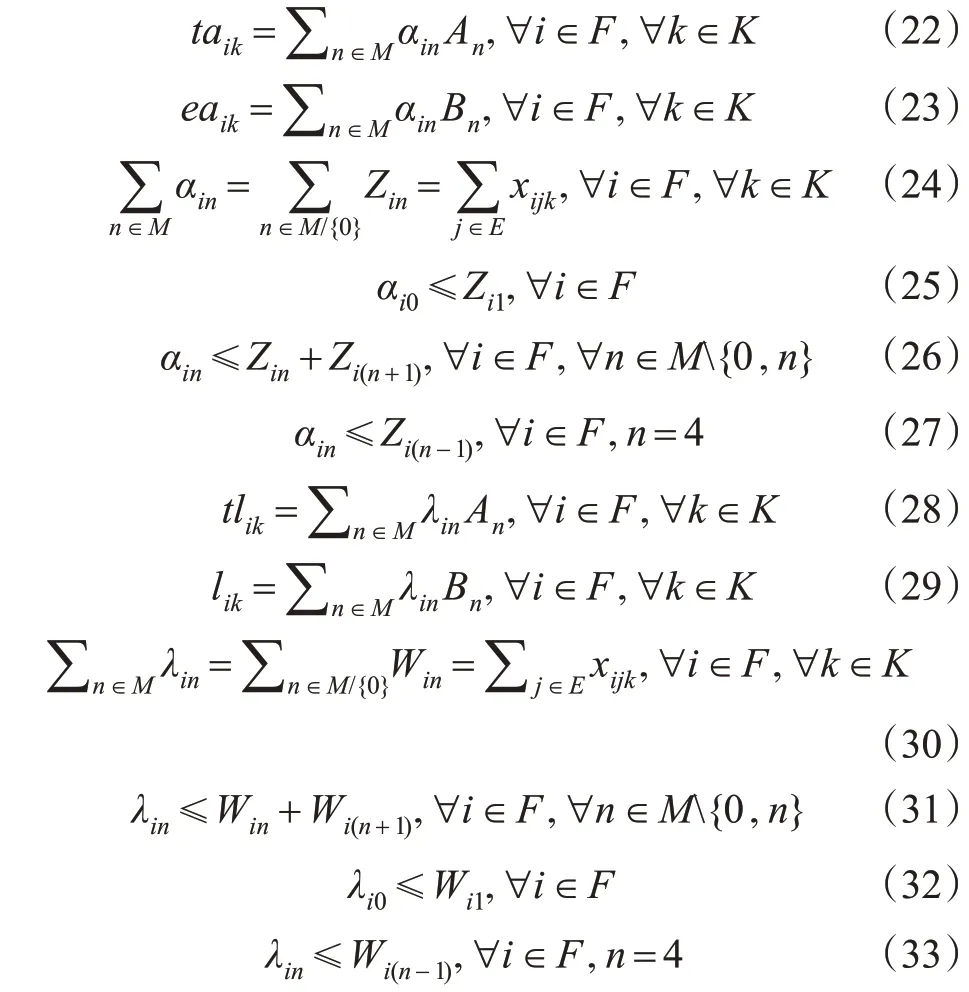
式（22）~（27）表示车辆到达充电站时，电量和充电时间用分段充电函数e(t)表示的约束，式（28）~（34）表示车辆离开充电站时，电量和充电时间用分段充电函数e(t)表示的约束。

模型涉及的决策变量取值见式（34）~（38）。

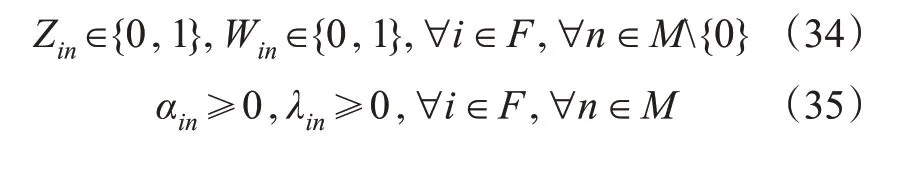
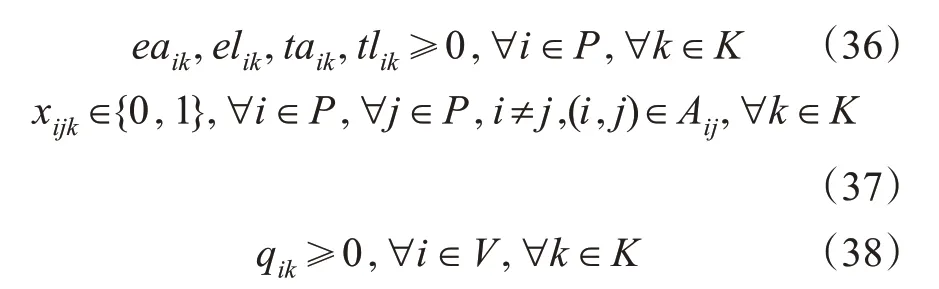
上述模型可求得成本最小的物流配送路径，其通过充电量计算充电成本比以往研究中简单统计进入充电站次数来计算充电成本更加符合实际。在带硬时间窗的EVRP模型基础上增加了非线性充电函数，这与以往的EVRP-NL模型只考虑车场时间窗约束和单一充电方式不同，此模型针对物流配送问题特性，对每个物流点赋予时间窗约束，限制了充电站无限次充电从而导致的无效路径，并对每个充电站设定换电和非线性快充2种充电方式，增加了充电策略灵活性和结果多样性，更加符合物流配送特征。

2 模拟算例分析

2.1 数据来源及参数取值

为了验证模型的可行性，采用了VRP问题常用的Solomon测试数据集作为模拟算例。Solomon数据集由6种不同类型的数据集组成（C1，C2，R1，R2，RC1和RC2），每个数据集包含800~1 200条客户数据。RC，R，C这3类数据特征分别为：①RC：兼具散点和集群客户的组合数据；②R：在一定范围内均匀随机分布的客户数据；③C：集群客户数据，其时间窗口是基于已知解决方案生成的。

其中类型1表示时间窗和容量限制较严格，类型2表示时间窗和容量限制较松弛[19]。

本 研 究 选 取RC101，R101，C101，RC201，R201，C201这6组数据集，分别选取各数据集的任意25条数据，其信息包括各点的时间窗、坐标、需求量、车辆的额定载重，其中C=200 kg。本文研究的物流运输属于短距离末端物流运输的小规模算例，适合纯电动物流车作业。其余参数参考具备换电和快充2种充电装置的纯电动物流车远程E200和宋稚雅[20]关于短距离小规模电动物流车的研究中的部分数据进行取值，各参数设置见表2。

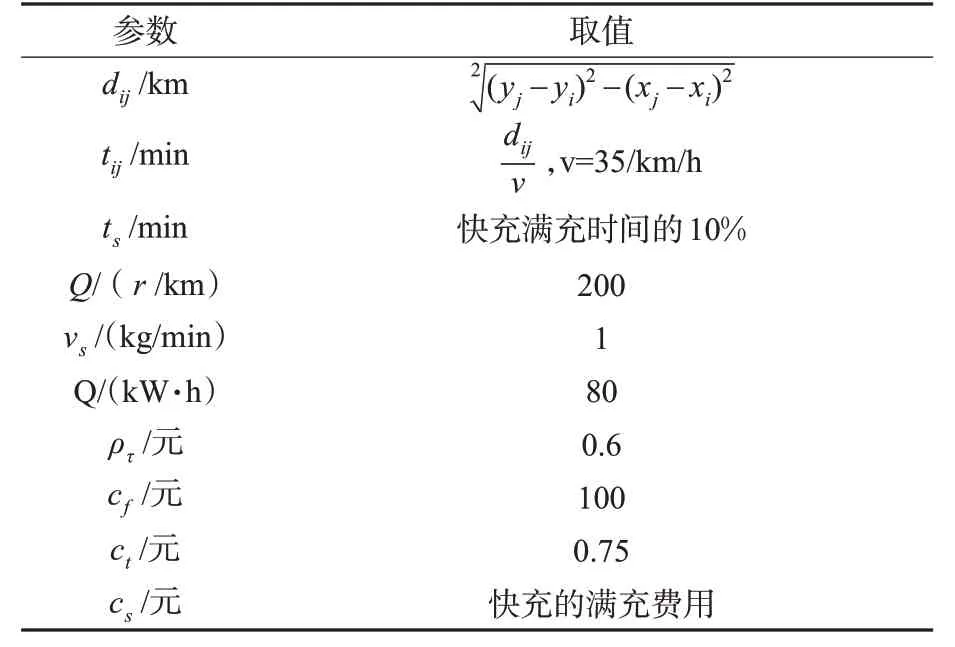
表2 相关参数设置Tab.2 Related parameter settings

2.2 模型可行性验证

本研究设节点25为配送中心，节点20~24为充电站，节点0~19为客户点。实际物流配送中心的时间窗设为[06：00，08：00]，即T1=840 min，由于Solomon数据集每组算例给定了各自的配送中心时间窗，如RC101的T2=230 min，定义时间比θ=T2/T1，式（39）~（43）为时间相关参数换算公式，换算结果见表3。

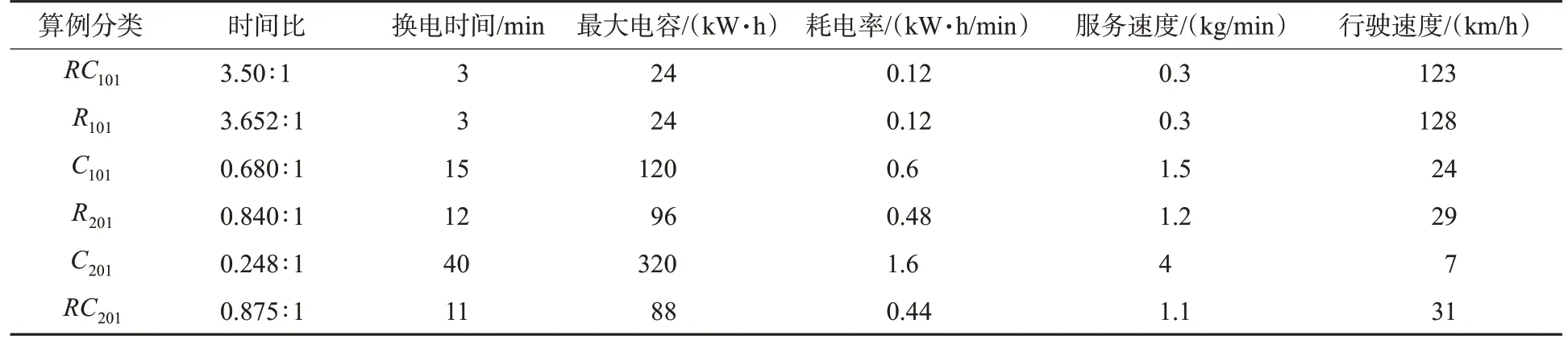
表3 每种算例的时间参数Tab.3 Time parameters of each example

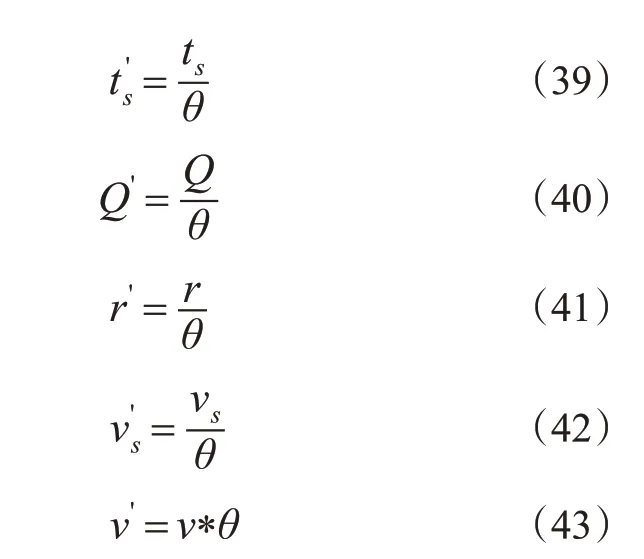
对以上算例，使用64位Windows 10系统，处理器为英特尔i5-4590@3.3GHz，内存为8G的联想扬天T4900c-00台式电脑进行计算。利用Python 3.8调用Gurobi 9.1.2，将约束转化为代码进行反复求解，实验发现设置4辆纯电动货车进行配送计算结果更为合理，因此设K=4。8组算例求解用时均不超过8 h，其中Gap=(obj-lowerbound)/lowerbound。8组求解结果见表4，其中RC101算例具体的配送路径见表5，路径图见图4。

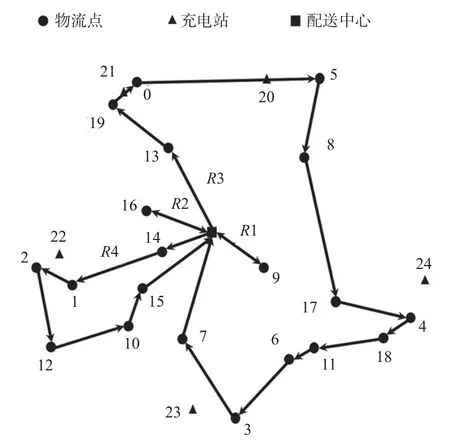
图4 模拟算例配送路径示意图Fig.4 Schematic diagram of distribution path of simulation example

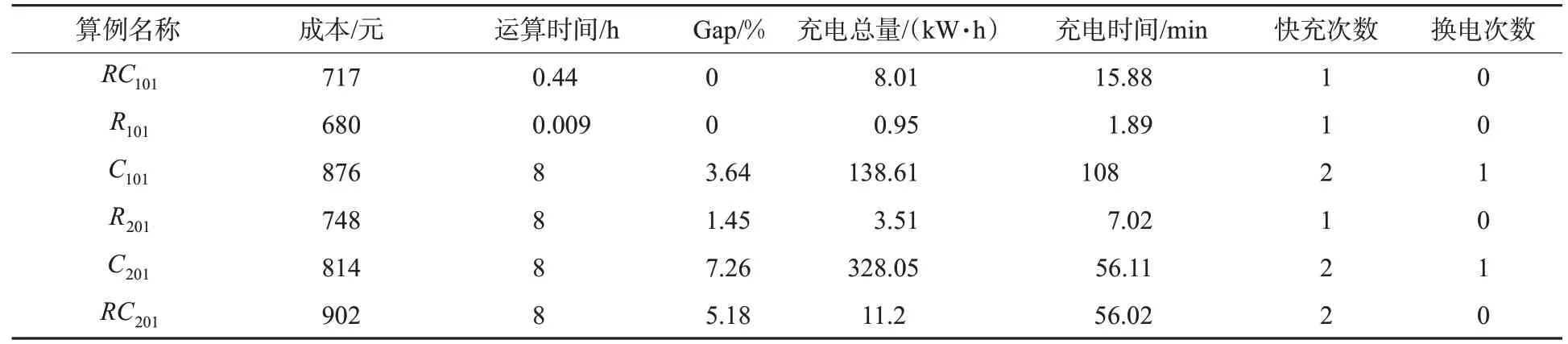
表4 模拟算例求解结果Tab.4 The solution results of simulation examples

表5 模拟算例配送路径Tab.5 Distribution path of simulation examples

从表4可见：Gurobi求解器可以求解代入不同类型数据的模型，并得出对应的车辆配送路径以及充电相关结果，这说明本研究提出的模型和方法对于求解小规模算例的电动车路径规划问题具有可行性和普适性。第3节使用的实际数据类型为C类集群客户，从求解结果可知Gurobi对C类集群客户的求解效率较慢，Gap值较大，因此在求解实际算例时，需要考虑增加求解时间，使求解更彻底。

3 实例分析

四川省简阳市面积2 213.5 km2，毗邻成都天府国际机场和双流国际机场，是多家物流公司的中转集中地，负责下设25个乡镇的物流配送工作。本研究对某通快递公司在简阳市的末端物流配送路径进行优化，客户点为25个乡镇快递点，编号0~24；充电站为简阳水东充电站、特来电充电站和简阳汽车充电站，编号25~27；配送中心为简阳市某通快递分拣中心，编号28。

代码运行时间以min计算，开始时刻记为0。例如，配送中心06：00开始营业，20：00结束营业，其配送中心时间窗为[0，840]min，且时间比θ=1，其他相关参数可直接使用表2数据。实际算例位置见图5，各点需求量和时间窗约束见表6。

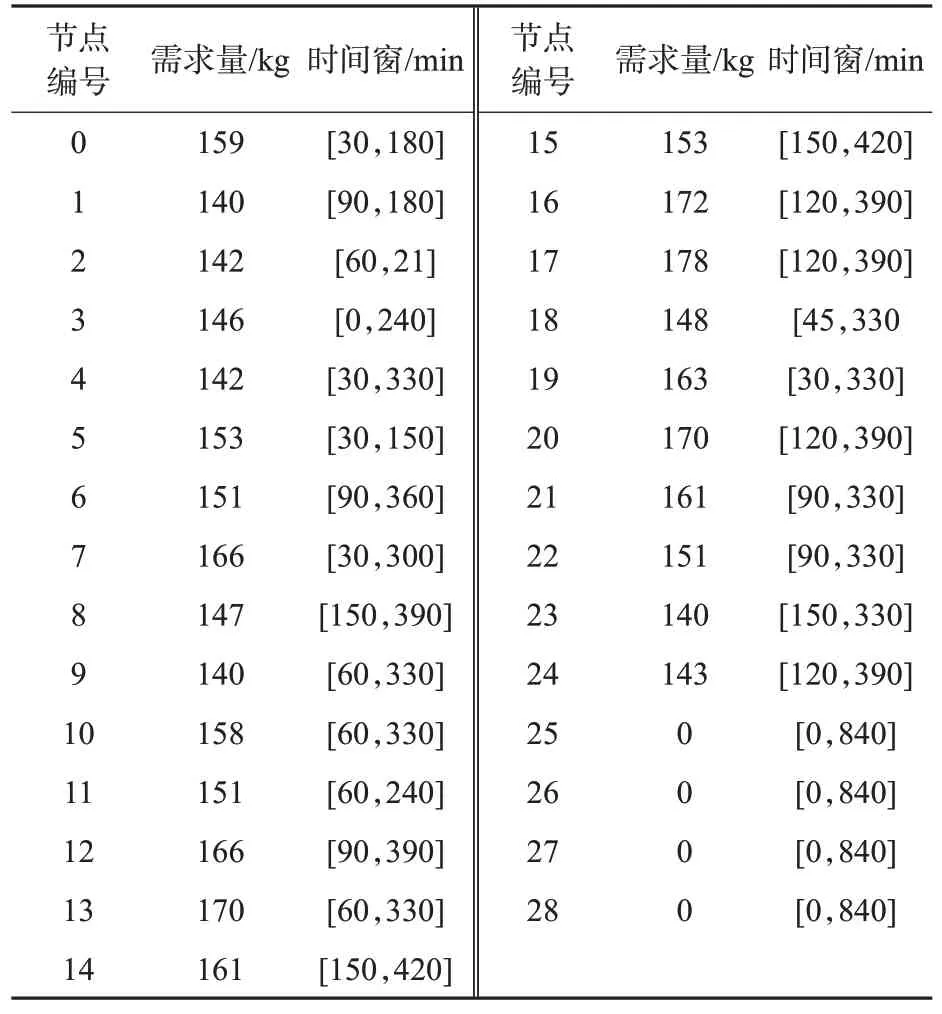
表6 实际算例基础数据Tab.6 The basic data of actual examples

图5 实际算例各点位置示意图Fig.5 Location diagram of each point in the actual examples

实际算例中，配送车辆仍使用纯电动物流车远程E200，其C=1 000 kg，模型参数还需要进行以下调整。

1）车辆以直线距离代入模型中计算会造成较大的误差，通常在直线距离基础上乘以道路迂回系数σ（σ=2），得到

2）车辆载重越大，耗电率越大，其实际的耗电率比0.4大，本研究设置耗电率r为0.67。

3）按照简阳特来电充电站收费情况，结合分时电价原则，ρτ取0.6元（/kW·h）。

4）由2.2可知，求解器在求解集群客户数据集时求解速度较慢，因此将求解时间从8 h调整为12 h，以便得到更彻底的求解结果。其余参数与模拟算例相同。多次变换ρτ和cs的取值，对电价进行灵敏度分析，具体电价取值表见表7，求解结果见图6~7。

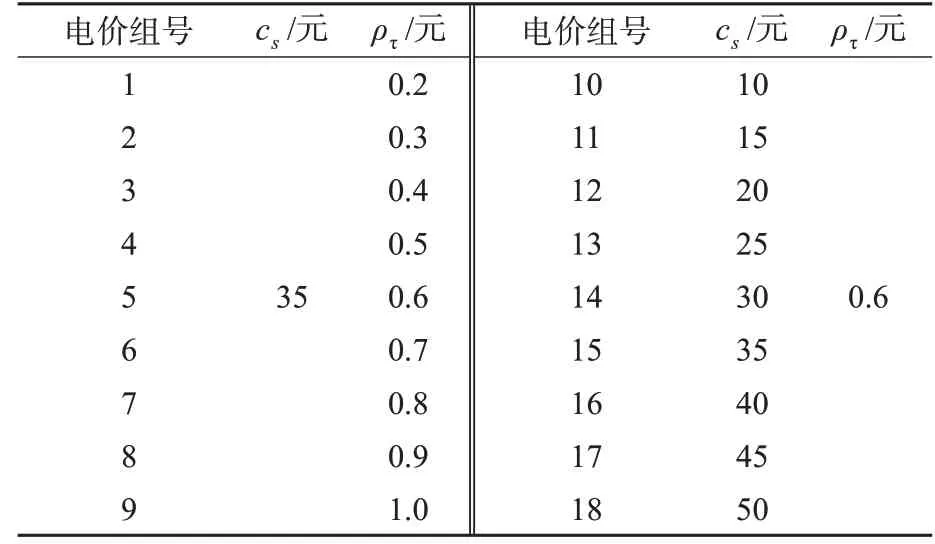
表7 电价组别Tab.7 electricity price group

据图6和图7可知：当cs=35元/次，ρτ为0.2，0.3，0.4元/（kW·h）时，车辆选择单一快充策略（single fast charging strategy-linear，SFCS-L）；ρτ为0.5，0.6，0.7，0.8元/（kW·h）时，车辆选择FCS-NL；ρτ为0.9元/（kW·h）及更高时，车辆选择单一换电策略（single change stratrgy，SCS）。可知当ρτ较低时，车辆选择ICS-L，随着ρτ逐渐升高，车辆快充电量不断减少，换电电量不断增加，充电成本随着ρτ升高而升高，当ρτ升高至0.9元/（kW·h）及更高时，车辆充电策略由ICS-L变为ICS-C，且充电成本和充电策略均不再变化。

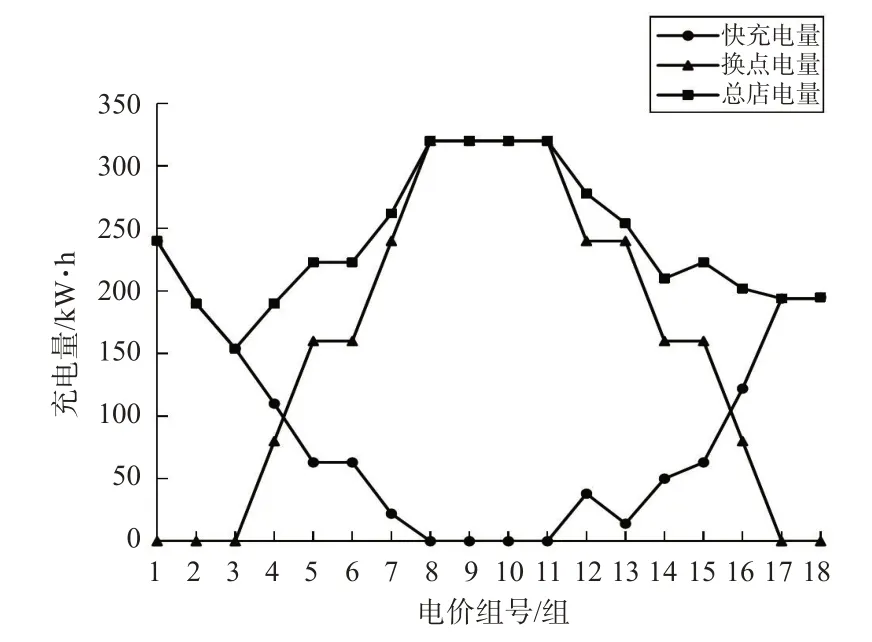
图6 电价变化对充电电量的影响Fig.6 Influence of electricity price change on charging power

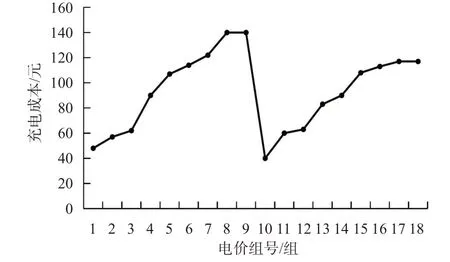
图7 电价变化对充电成本的影响Fig.7 Influence of electricity price change on charging cost

当ρτ=0.6元/（kW·h），cs为10，15元/次时，车辆选择ICS-C；cs为20，30，40元/次时，车辆选择FCS-NL；cs为45，50元/次，车辆选择ICS-L。可知当cs较低时，车辆选择ICS-C，随着cs逐渐升高，车辆换电电量不断减少，快充电量不断增加，充电成本随着cs升高而升高，但当cs升高至45元/次及更高时，车辆充电策略从ICS-C变为ICS-L，且充电成本和充电策略均不再变化。

选取表7中车辆选择FCS-NL时的所有电价组合，即电价组别4、5、6、7、12、13、14、15、16，其中6组和15组电价组合相同，只取第6组进行横向比较。

为分别构建可实现ICS-C、ICS-L和可选择换电或线性快充的线性混合充电策略（hybrid charging strategy-linear，HCS-L）的EVRP模型，需将原模型进行如下改变。

1）将原EVRP-NL模型中式（23）~（34）删去，添加约束zik=0，∀i∊F,∀k∊K，可实现ICS-C。

2）将原EVRP-NL模型中的式（23）~（34）删去，添加约束yik=0，∀i∊F,∀k∊K，可实现ICS-L。

3）将原EVRP-NL模型中的式（23）~（34）删去，其余约束保持不变，设充电速率g为1（kW·h）/min，可实现FCS。

通过计算发现4种策略的行驶距离相近，即4种策略的行驶时间和行驶成本相近。因此本研究只比较了不同充电策略的充电成本和充电时间的结果，见图8~9。

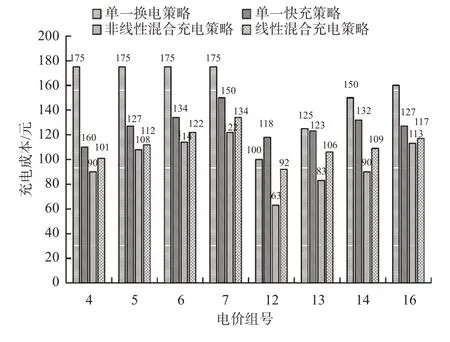
图8 不同充电策略的充电成本比较Fig.8 Comparison of charging costs of different chargingstrategies

根据图8和图9可知，8组电价中，混合充电策略对减少车辆充电成本和充电时间都具有明显的优越性。其中，FCS-NL的充电成本比ICS-C减少35%，比ICS-L减少24%；FCS的充电成本比ICS-C减少31%，比ICS-L减少13%；FCS-NL的充电成本比FCS减少12%。FCS-NL的充电时间比ICS-L减少69%，比ICS-C减少3%；FCS的充电时间比ICS-L减少55%，比ICS-C增多29%，FCS-NL的充电时间比FCS减少31%。可知本研究设计的FCS-NL能够有效减少选择ICS-C和ICS-L时电动车物流配送的充电成本和充电时间，且比FCS更优越。

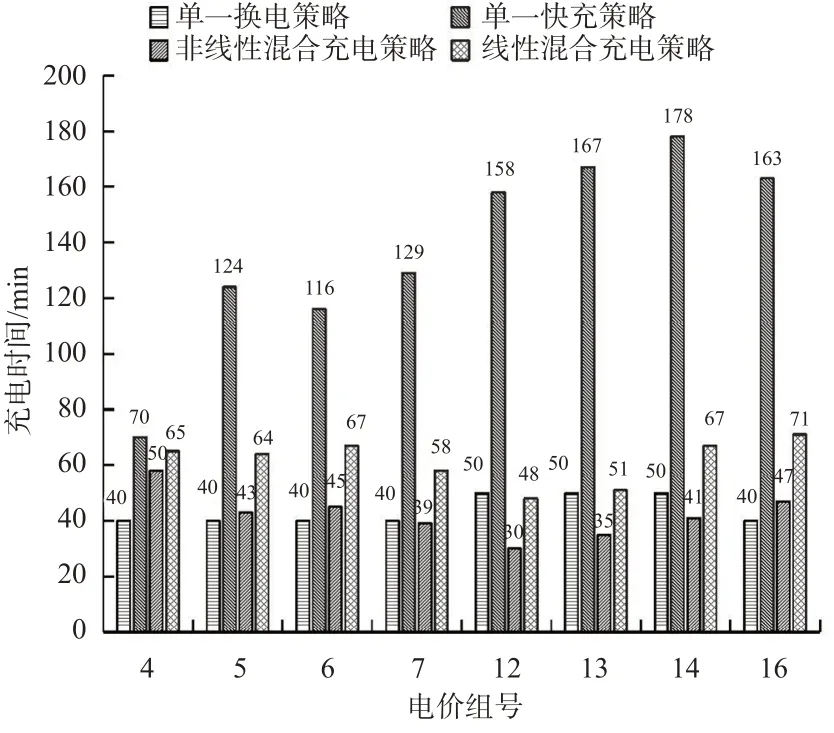
图9 不同充电策略的充电时间比较Fig.9 Comparison of charging time of different charging strategies

从以往不同充电策略的电动车路径规划结果来看，在使用同一数据集的情况下，Verma等[5]得出ICS-C在总成本、运送时间方面均优于FCS，这是由于软时间窗及惩罚成本的设定，使ICS-L和FCS都因为产生延迟成本从而导致总成本更高；Keskin等[6]、郭放等[21]均得出部分线性充电策略（partial charging strateegy-linear，PCS-L）在配送时间、车辆数量、总成本方面均优于完全线性充电策略（complete charging strategy-linear，CCS-L），且在部分充电量越多、时间窗限制越严，其优越性越明显；而Montoya等[14]则发现EVRP-NL模型可同时实现PICS-L，且FCS-NL能有效减少总成本和车辆数。本文在上述研究结果基础上，控制车辆数恒定，从ICS-C、ICS-L、FCS、FCS-NL（包含PICS-L）这4种充电策略在实际算例中的成本、时间2个维度上进行比较，首次提出了FCS和FCS-NL的对比，发现FCS-NL是4种策略中最优越的。在以往ICS-L与ICS-C的对比基础上，进一步提出FCS与ICS-C的对比，发现在没有延迟成本，时间窗约束相对松弛的模型中，在成本方面ICS-C不如FCS优越，但仍可以节约充电时间。

4 结束语

本文在以往研究基础上，根据实际充电过程采用部分估值验证法，用3段分段函数拟合非线性充电函数，构建了以最小化成本为目标函数，考虑硬时间窗、载重、电量及充电函数线性化约束的电动车物流配送路径规划模型。利用Gurobi求解器验证了模型在6组Solomon数据中的可行性和普适性。通过改变快充电价或换电电价将实际算例求解结果进行纵向对比，证明总成本随电价升高而升高，充电策略则向电价更低的充电方式变化，且电价升高至一定程度，充电策略和总成本将不再变化。最后在以往只研究2种充电方式的充电策略对比基础上，将ICS-C、ICS-L、FCS、FCS-NL（包含PICS-L）这4种充电策略在8组电价组合下的计算结果进行横向对比，充电成本优越性排序为：FCS-NL>FCS>ICS-L>ICS-C，充电时间优越性排序为：FCS-NL>ICS-C>FCS>ICS-L。可证明本研究设计的FCS-NL在减少配送成本和时间方面都具有显著优越性。下一步研究可设计混合启发式算法，如ALNS等改进计算速率和精度，并对比各种算法和求解器求解的优劣。