鞍钢蒸汽管网运行模型的开发和应用

贾振，刘柏寒，赵乐岩，何嵩，李丛康，张天赋

（1.鞍钢集团钢铁研究院，辽宁 鞍山 114009；2.鞍钢股份有限公司能源管控中心，辽宁 鞍山 114011）

鞍山钢铁集团有限公司本部（以下简称“鞍钢本部”）蒸汽管网系统庞杂，作为蒸汽系统重要组成部分之一，存在计量监测设备配备不齐全，监测手段不健全，以及现有的计量仪表精度有所偏差等问题，从而导致对管道内蒸汽运行状况和设备运行状态不清晰。为解决蒸汽管网系统存在的问题，适应公司能源介质智能化管控的需求，开发鞍钢蒸汽管网运行模型和在线监测系统显得尤为重要。为此，根据鞍钢蒸汽管网结构分布特点、运行模式以及蒸汽在管道内流动的物理过程，建立了蒸汽在管网内流动过程数学模型，模型应用后提升了鞍钢蒸汽管网的监测水平，本文对此做一介绍。

1 鞍钢本部蒸汽供应方式

鞍钢本部蒸汽资源丰富，夏季用汽量相对较小，以各工序余热回收蒸汽为主，自备电厂的蒸汽为辅。冬季随着厂房采暖、设备伴热等用户的增加，用汽量相对较大，以自备电厂的蒸汽为主，各工序余热回收蒸汽为辅。汽源分布相对集中，为用户提供3种不同能级的蒸汽，通过公司蒸汽管网输送至用户。鞍钢本部蒸汽供求关系见图1。用户较分散，需要的蒸汽能级参差不齐，造成了蒸汽管网系统庞大，管网运行状态不利于监测、调控。

图1 鞍钢本部蒸汽供求关系图Fig.1 Steam Supply-demand Relation Diagram in Anshan Works of Ansteel

2 蒸汽管网运行模型

蒸汽管网运行模型的基础是蒸汽在管道内流动过程的数学模型。蒸汽在管网内流动是一个比较复杂的物理过程，这不仅要考虑由于管道阻力造成的压力损失，管道内部与环境之间的散热损失，还要考虑因为管道间连接关系的改变而引起的运行方式的变化，即蒸汽流向的改变，以及汽源和用户间供应方式的改变。模型主要由管网拓扑模型、水蒸汽水力学模型和水蒸汽热力学模型等组成。

2.1 管网拓扑模型

管网拓扑模型是反映蒸汽管道中节点与管段间关系的重要模型。该模型的作用是根据管网中管段与节点间的位置关系，依据图论的基本原理，建立管段-节点关联矩阵，即衔接矩阵。

衔接矩阵是描述管网结构信息较为常见、简单的方法之一。对管网图中的节点和管段逐一编号，编号为i的节点，其信息记在表中i行，编号为j的管段，其信息记录在j列。衔接矩阵中各元素的表示方法是：

2.2 蒸汽流动过程数学模型

蒸汽在管道内流动过程数学模型的计算主要包括水蒸汽物性参数计算、管段水力学计算（水蒸汽水力学模型）、管段热力学计算（水蒸汽热力学模型）等三部分内容。组建的方程主要有节点方程（连续方程）、管段压降方程和能量方程。

2.2.1 水和水蒸汽物性参数计算

依据国际水和水蒸汽协会于1997年9月采纳的一套工业用水和水蒸汽物性参数计算公式（IAPWS-IF97）[1]，计算水蒸汽的比热、比容、焓等物性参数。

2.2.2 节点方程（连续方程）

节点方程满足质量守恒定理。任意节点处的流量之和等于流入、流出该节点的流量之和，即任意节点处的流量代数和等于零。设流出节点的流量为正，流入节点的流量为负，则：

式中，qi为节点 i的流量，kg/s；qij为与节点 i相连接的各管段流量，kg/s；i，j表示起点、终点处的节点编号。

2.2.3 管段压降方程

管段压降方程主要是用来描述管段水头损失与其两端节点压力关系式的管道压降方程。通过计算划分的管段压降进而求出管段两端节点的压力。

式中，pij为管段蒸汽压降，Pa；pi、pj为管段两端节点 i，j处的水蒸汽压力，Pa；εi为管段的摩擦阻力损失系数；qij为管段蒸汽流量，kg/s。

2.2.4 管段能量方程

管道内输送的蒸汽温度远高于环境温度，与环境间存在较大的热量交换，导致蒸汽在管道内流动时温降较大。蒸汽温度的变化会直接影响到压力、比热、比容等物性参数的变化，而这些参数的变化又会直接影响到蒸汽管网的水力计算。因此，在进行蒸汽管网水力计算的同时，还要兼顾蒸汽管网的热力计算。

管段能量方程的作用主要是通过求解划分管段的温降，进而求出管段两端的节点温度。依据蒸汽管道的结构（见图2），采用傅立叶导热公式[2]，单位长度管段内的蒸汽与环境之间散热损失公式是：

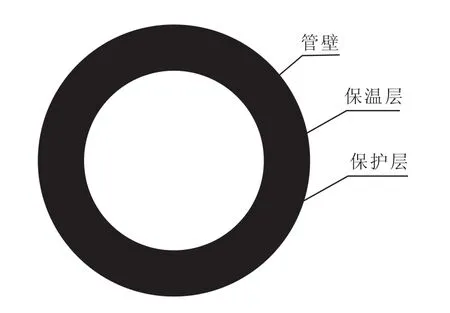
图2 管道结构示意图Fig.2 Schematic Diagram of Pipeline Structure

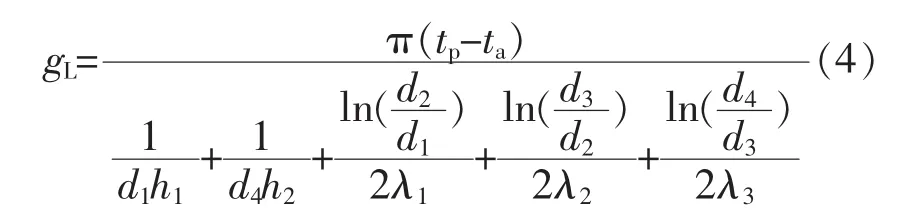
式中，gL为单位长度管段的蒸汽与环境之间的散热损失，W/m；tp、ta分别表示管段内蒸汽的平均温度、 环境温度，℃；d1、d2、d3、d4分别表示蒸汽管道内径、蒸汽管道外径、保温层外径、保护层外径，m；h1、h2分别表示蒸汽与管道内壁之间的对流换热系数、环境与蒸汽管道保护层之间的对流换热系数，W/（m2·℃）；λ1、λ2、λ3分别表示钢管导热系数、保温层导热系数、保护层导热系数，W/（m2·℃）。

管段内蒸汽的热量损失的表达式是：

式中，gy为单位时间管段的散热损失，kJ/s；qij为管段的蒸汽流速，kg/s；Cpij为蒸汽平均比热，kJ/（kg·℃）；ti、tj分别表示管段起点和终点处的蒸汽温度，℃。

式（3）与式（4）联立，则：

式中，η为局部散热损失修正系数；L为管段长度，m。

3 应用结果分析

以鞍钢本部厂内一段输送中压过热蒸汽的管网为例，采用牛顿迭代算法实时计算蒸汽管网流动过程数学模型组建的非线性方程组。管网拓扑关系见图3。图中，节点1、5表示汽源，节点4表示用户，节点2、3和6则是内部节点，A、B是管网中安装的阀门。

图3 管网拓扑关系图Fig.3 Topology Diagram for Pipeline Network

根据生产实际情况，在线实时模拟计算结果见图4。图4中的蒸汽输送生产工艺是节点1作为用户主要汽源，常年使用，节点5作为备用汽源，只有节点1检修时才投入使用。计算时，节点5至阀门B之间的管道未投入使用。节点1的曲线是蒸汽管道配备的计量仪表采集的实时生产数据，作为计算节点2、3、4的初始条件参与计算。节点2、3、4处的曲线是计算得到的实时蒸汽流动过程参数变化曲线。

图4 在线实时模拟计算结果Fig.4 Online Real-time Analogy Calculation Results

由图4可知，节点2和节点3的温降、压降变化不太明显，温度和压力曲线基本重合，变化较小。主要原因是节点2的位置在阀门A前，节点3的位置在阀门A后，两点距离较近，阀门开度较大，不低于80%，阀门造成的局部阻力损失相对较小，表明模型计算结果与管道实际运行状况趋势相符。用户端节点4距离汽源端节点1大约2.3 km，通过模型计算得到的这两点的压差均在0.2 MPa左右，说明模型计算结果与管道压力损失经验值基本一致。

综上，依据建立的蒸汽流动数学模型，结合现场实际生产工艺计算得到的2、3、4节点的温度和压力变化趋势基本符合蒸汽在管道内运行的实际状况，能够较为准确地评价蒸汽参数在管网中的衰减程度，有效满足蒸汽生产调度人员对管网进行实时监测的需求。

4 结语

依据蒸汽管网结构分布特点和运行模式，通过引入管段与节点之间关系等概念，以及综合考虑蒸汽压降和温降等因素的相互影响，建立的蒸汽管网运行模型能够较为真实地反映蒸汽在管道内的流动物理过程的变化规律，能够帮助蒸汽管网调度人员了解蒸汽在管网内的流动状态和参数变化情况。应用后提升了鞍钢蒸汽管网的监测水平。