考虑铁心非线性的三相立体卷铁心变压器建模及空载特性分析

杨北超 范学鑫 王瑞田 张新生 揭贵生

（海军工程大学舰船综合电力国防科技重点实验室 武汉 430033）

0 引言

相对于三相平面叠铁心变压器，立体卷铁心变压器具有磁路对称、振动噪声低等优势，近年来广泛应用于高层建筑、地铁、新能源接入等场合。通过对电工钢带进行卷绕加工，得到截面为近似半圆形的铁心框，将三个尺寸相同的铁心框两两拼接，构成三角形立体结构铁心，典型结构如图1所示。

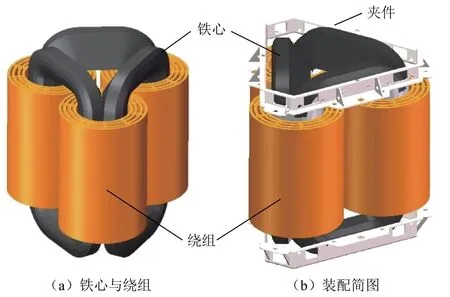
图1 立体卷铁心变压器 Fig. 1 3D wound core transformer

立体卷铁心三相磁路长度相同，导磁方向与硅钢片轧制方向相同，结构对称合理，而常规叠铁心三相磁路长度不对称，硅钢片接缝处搭接存在气隙。在同等变压器指标要求下，立体卷铁心通常比传统叠片铁心节省硅钢材料约20%[1]。因此，立体卷结构在电力电子电能变换领域具有广阔的应用前景。为了提高功率密度，应尽可能提高变压器铁心工作磁密幅值，因此迫切需要准确评估立体卷铁心变压器在饱和边界状态的工作特性。

在立体卷铁心磁路工作特性方面，文献[2]给出了磁路约束方程，并采用拉格朗日函数极值分析方法和枚举法分析了单框磁通谐波成分。文献[3]推导了立体卷铁心变压器的H平衡方程，研究了三相平衡励磁条件下立体卷铁心的磁通密度。文献[4]应用硅钢片材料特性曲线分析了立体卷铁心变压器的空载损耗。但以上文献未深入研究铁心非线性对变压器工作特性的影响。

在变压器铁心非线性建模方面，目前主要可以分为Preisach模型、Jiles–Atherton（J-A）模型、等效电路模型三类。

Preisach模型：美国马里兰州立大学的Mayergoyz将输出随时间的变化率引入分布函数，得到了动态Preisach模型，以标量磁滞单元为基础，提出了矢量Preisach模型[5]。文献[6]基于Preisach磁滞模型，提出了面向非对称磁滞回线模拟的参数辨识方法，并应用于静态磁滞特性模拟。文献[7]提出了一种适用于100kW双有源桥式变换器的三相中频变压器的修正Preisach模型，并提出优化的Preisach分布函数参数识别方法。

Jiles-Atherton模型：结合微观结构参数和材料的宏观特性，基于磁畴运动假设，用磁畴壁运动的一个耦合系数和一个抵制系数来描述磁矩的相互作用，对铁心的动态磁化过程进行准确的模拟[8]。文献[9]提出一种基于模拟退火（Simulated Annealing, SA）与Levengerg-Marquardt（L-M）混合的J-A模型参数提取方法。文献[10]利用J-A磁滞模型描述变压器铁心的非线性特性，得到二次电压幅值和相位用于分析变压器一次侧短路故障。

等效电路模型：文献[11]指出在阻尼衰减、正弦稳态等工作条件下并不需要非常精确的磁滞模型，建立了基于高阶多项式的等效磁滞模型。文献[12]基于代数方法，使用非线性电感、非线性电阻并联形式反映铁心材料的非线性特征。文献[13]改进了上述模型，在非线性电阻的参数求取时考虑了空载损耗试验结果，优势在于模型简单，便于电路仿真应用，不足之处是准确性受限，模型适应性较差。

在立体卷铁心变压器FEM建模方面，目前文献报道较少。文献[14]建立1MV·A立体卷铁心干式配电变压器三维有限元模型（Finite Element Model, FEM）仿真模型，通过仿真进行铁耗计算。文献[15]建立了简化单柱二维电磁场模型，分析了绕组漏磁。

本文开展了考虑铁心非线性的三相立体卷铁心变压器建模及空载特性分析。建立了考虑饱和、磁滞特性的三相立体卷铁心变压器非线性磁路模型与FEM二维等效模型。最后搭建80kV·A立体卷铁心变压器试验平台，验证了模型的准确性。

1 磁路建模与分析

1.1 立体卷铁心磁路模型

立体卷铁心由AB单框、BC单框、CA单框三个单框拼接组成，其中CA单框和AB单框组成A相心柱，AB单框和BC单框组成B相心柱，BC单框和CA单框组成C相心柱，如图2所示。

记立体卷铁心三个单框中流过的磁通分别为ΦAB(t)、ΦBC(t)、ΦCA(t)，A相、B相、C相心柱平均磁通分别为ΦA(t)、ΦB(t)、ΦC(t)，根据各单框磁通与心柱平均磁通之间的关系可得约束方程

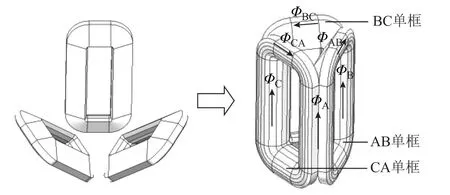
图2 立体卷铁心变压器磁通分布图 Fig.2 Flux distribution of transform with threedimensional wound core

由式（1）可知，ΦA(t)+ΦB(t)+ΦC(t)=0。记初级绕组匝数为NP，次级绕组匝数为NS，各单框磁阻分别为RmAB、RmBC、RmCA，三相励磁电流分别为IA(t)、IB(t)、IC(t)，二次电流分别为Ia(t)、Ib(t)、Ic(t)。二次绕组开路时，相应磁动势Fa~Fc为零。基于磁路欧姆定律构建约束方程[2]为

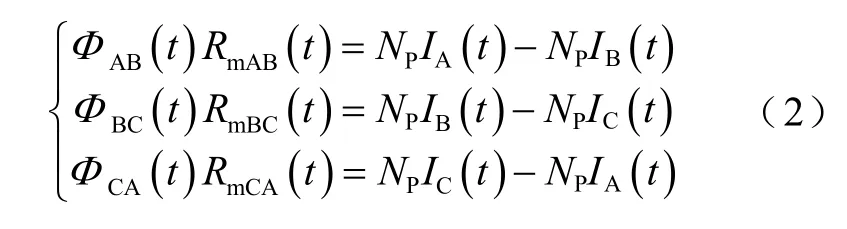
由式（2）可得

由于铁心材料的非线性特性，各单框铁心的磁化曲线与其当前工作点及历史轨迹相关。当各单框磁路工作点均位于磁化曲线线性段时，各单框磁阻基本相等，则

根据以上理论分析，建立立体卷铁心变压器等效磁路如图3所示。可知ΦAB、ΦBC、ΦCA形成闭合环路，存在零序磁通通路。

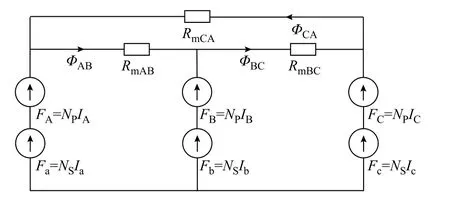
图3 立体卷铁心变压器等效磁路 Fig.3 Equivalent magnetic circuit of 3D wound core transformer

在理想正弦波电压源激励下，单框铁心磁通仅含基波分量和零序谐波分量[2]。由式（1）可知，心 柱处磁通由两个单框的基波分量和零序谐波分量合成，其中两个单框的零序谐波分量相互抵消，故心柱处磁通主要由两个单框的基波分量合成，如图4所示，图中ΦAB1、ΦBC1、ΦCA1为单框磁通的基波分量。由图4可得。由于心柱处截面积是单框截面积的2倍，故心柱平均磁通密度幅值为单框基波磁通密度幅值的0.866倍。

图4 单框磁通与心柱磁通相量图 Fig.4 Flux phasor diagram of Single frame and core column

1.2 立体卷铁心磁滞模型

根据变压器铁心磁化机理，本文采用J-A磁滞模型建立立体卷铁心变压器非线性磁路模型。J-A磁滞模型物理意义明确，能够较准确地描述磁感应强度B与磁场强度H的非线性关系。该磁滞模型将实际磁化强度M分为可逆磁化强度Mrev与不可逆磁化强度Mirr两部分，即

J-A正模型为[16]

式中，δ为方向系数，当dH/dt＞0时，δ=1，当dH/dt＜0时，δ=-1；k为磁畴间的牵制系数；α为磁畴内部耦合平均场参数；c为可逆磁化系数；Man为无磁滞磁化强度；δM是为了避免式（6）出现非物理解而引入的系数，即

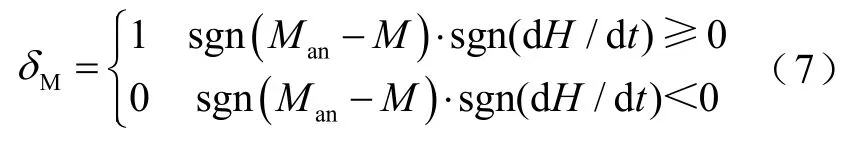
Man为

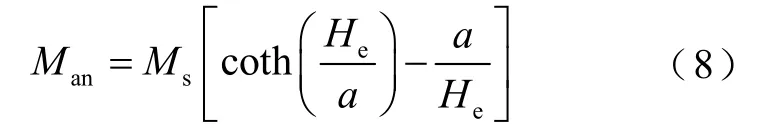
式中，Ms为饱和磁化强度；He为有效磁场强度；a为无磁滞磁化曲线形状参数。

以实测与计算的磁滞回线误差最小为优化目标，通过优化算法确定J-A模型的参数[9]。目前，该类算法主要包括遗传算法、粒子群算法[17]、人工鱼群算法、蛙跳算法[18]和模拟退火算法[9]及两两之间的混合算法[19]等。

本文采用GlobalSearch(GS)算法对五个模型参数进行辨识提取，GS算法是一种全局最优算法，在参数区间内使用分散搜索算法进行多次局部寻优，并对局部最优结果进行对比，返回目标函数全局的最小值和对应的参数[20-21]。

引入磁通密度B的方均根误差RMSE作为GS算法的目标函数，将J-A磁滞模型五个参数的提取问题转换为寻找目标函数全局最小值的优化问题。目标函数为

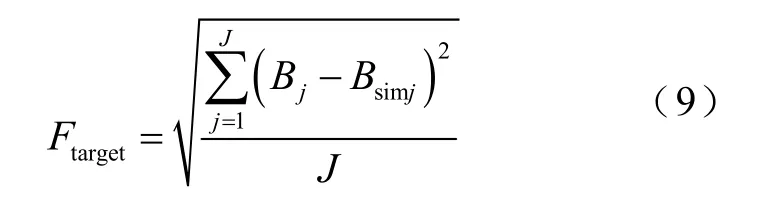
式中，Bj为磁通密度试验测量值；Bsimj为磁通密度计算值；J为采样个数。

使用GS全局最优算法辨识五个参数的上下限设置范围可参考表1[9]。

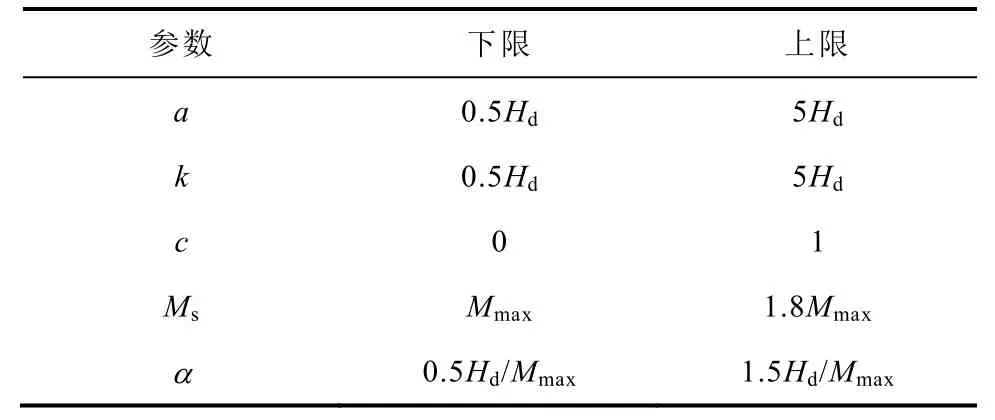
表1 J-A模型参数上下限范围 Tab.1 Range of J-A model parameters

表1中Hd为矫顽力，Mmax为磁化强度最大值。对于部分软磁材料，k取值近似等于Hd[16]。

根据本文样机所用硅钢片标准样片的实测磁滞回线数据，利用GS优化算法提取此材料的J-A模型参数为a=6.543A/m，k=16.653A/m，c=0.032 6，Ms=1.537×106A/m，α=1.640×10-5。GS优化算法求出的磁滞回线与硅钢片标准样片磁滞回线对比如图 5所示。可以看出，GS优化算法计算的磁滞回线在饱和区与实测曲线基本吻合，可以有效反映变压器在饱和状态的工作特性。

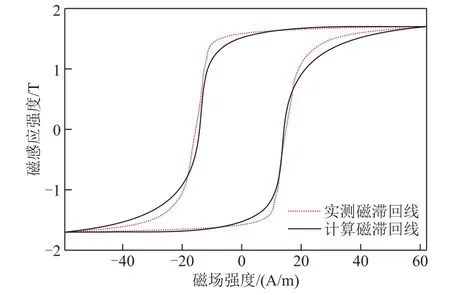
图5 GS算法计算与实测磁滞回线对比 Fig. 5 Hysteresis loop of the GS model and the measurement results

2 FEM建模与分析

平面叠铁心变压器通常在铁心窗口截面建立二维简化模型，而立体卷铁心变压器的各相铁心窗口截面不在同一平面，难以建立二维模型，而三维模型的计算精度与计算规模存在较大矛盾。

本文尝试提出一种立体卷铁心变压器有限元二维等效建模方法，便于开展变压器铁心工作特性的定量分析。

2.1 FEM二维等效模型

变压器所满足的电磁感应定律、安培定律公式为

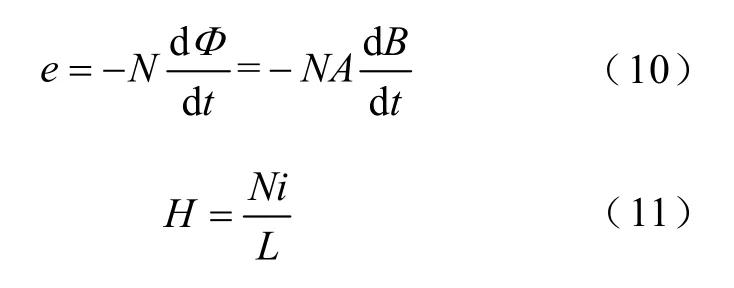
式中，e为感应电压；N为匝数；A为单框铁心截面积；i为电流；L为单框铁心磁路长度。

针对立体卷铁心变压器的结构特征，平行于铁心窗口，沿等边三角形展开为二维等效模型，同时设置周期性边界条件，建立立体卷铁心变压器二维等效模型如图6所示。二维等效建模时应当遵循上述变压器基本公式（10）、式（11），维持N、A、L不变，保持铁心和绕组主体结构不变，特别是铁心弯曲半径要与三维模型保持一致性。

图6 立体卷铁心变压器二维等效模型 Fig.6 Two-dimensional equivalent model of 3D wound core transformer

2.2 单框铁心等效模型参数确定

设定单框中轴线长度为磁路长度L，铁心窗口宽度为b，磁路宽度为w，将三维模型转换成二维模型时保持单框中轴线长度仍为L，同时b、w保持不变。单框铁心示意图如图7所示，图中h为铁心窗口高度。

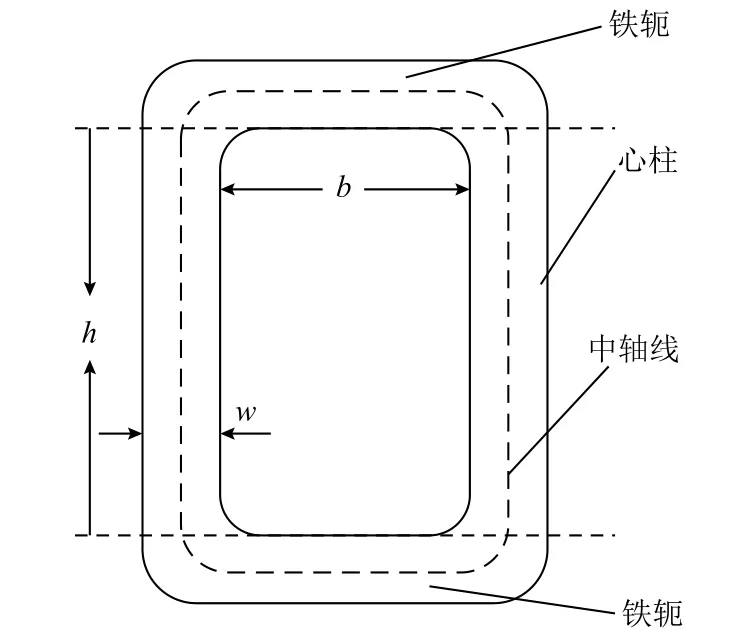
图7 单框铁心示意图 Fig.7 Single frame core

为保持单中心投影后单框铁心截面积A不变，磁路宽度w与二维模型深度d的关系式为

由图7可得磁路长度L计算公式为

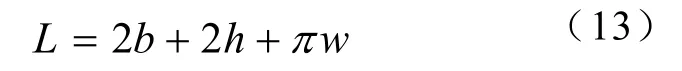
2.3 二维等效模型与三维模型对比

为了验证本文提出的二维等效模型计算的准确性与快速性，针对本文变压器样机案例（参数详见第4节），建立三维模型进行对比，网格剖分对比如图8所示。

图8 FEM三维模型与二维等效模型网格剖分对比 Fig.8 Comparison of mesh division between FEM 3D model and 2D equivalent model

以三相额定电压激励空载工况为例，立体卷铁心变压器矢量磁通密度分布及各单框磁通密度仿真结果对比如图9~图11所示，其中图11中的磁通密度是指三维模型或二维等效模型中铁心截面的平均磁密。

由图11可知，FEM二维等效模型与三维模型AB单框、BC单框、CA单框磁通密度幅值的仿真误差分别为0.89%、3.32%、0.58%，误差在允许范围内。

图9 FEM三维模型铁心矢量磁通密度 Fig.9 Core vector magnetic density in 3D FEM model

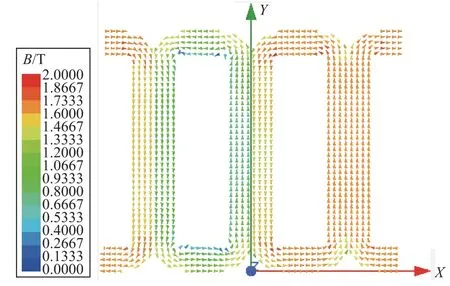
图10 FEM二维等效模型铁心矢量磁通密度 Fig.10 Core vector magnetic density in 2D equivalent FEM model

图11 二维等效模型与三维模型各单框磁通密度仿真值 Fig.11 Simulation results of single frame magnetic density in 2D equivalent model and 3D model

两种仿真模型使用同样的计算硬件条件，CPU型号Intel I5-9400F，计算内核共6核，仿真设置使用5核，主频2.90GHz，内存16GB，仿真文件存储在固态硬盘，二维等效模型与三维模型FEM仿真资源消耗情况见表2，表中磁通密度幅值是指三维模型或二维等效模型中铁心截面平均磁通密度的幅值。对比可知，二维等效模型与三维模型仿真得到的磁通密度幅值误差在允许范围内，但三维模型耗时长且占用大量内存空间，二维等效模型可以比三维模型缩短96.66%的仿真时间，减少92.93%的内存占用空间。另一方面，在仿真计算过程中发现三维模型不易收敛，仿真效率较低。

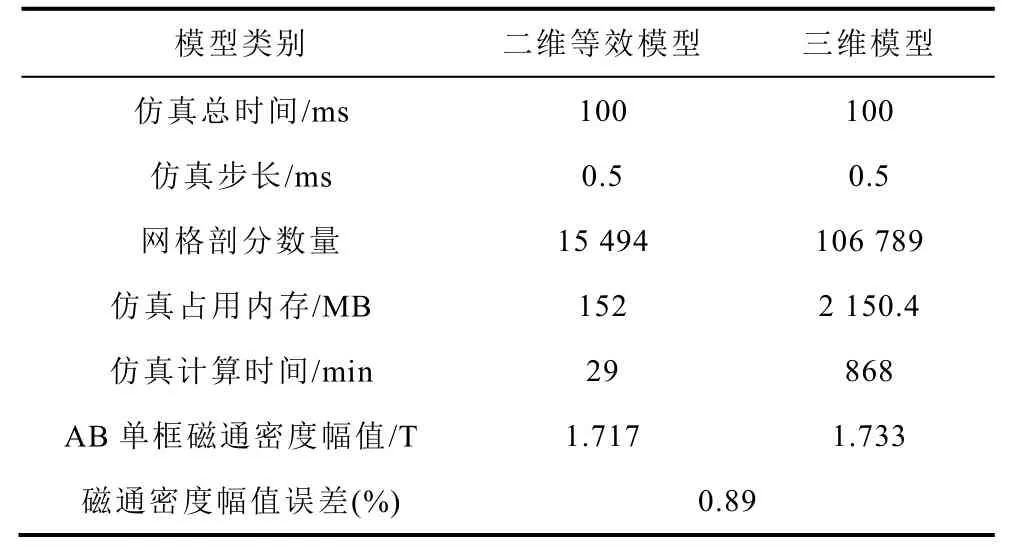
表2 仿真计算时间 Tab.2 Simulation calculation time

本文二维等效模型主要考虑铁心工作特性，通过有限元矢量磁滞法考虑铁心非线性的影响，也可同时考虑绕组损耗与漏感的影响。

3 非正弦激励下变压器的工作特性

根据图3立体卷铁心变压器等效磁路图，搭建立体卷铁心变压器非线性磁路模型，将GS优化算法提取的J-A模型参数代入磁路模型，分别设置正弦波、三角波、方波激励，添加给非线性磁路模型与FEM二维等效模型，验证非正弦激励下立体卷铁心变压器磁路模型的准确性与适用性。其中正弦波激励验证结果见第4节与试验对比部分。

3.1 三角波激励

三角波激励采用幅值为282.8V的三相电压激励，磁路模型计算结果与FEM二维等效模型仿真结果对比如图12所示。对比可知，磁路模型计算得到的励磁电流与二维等效模型仿真得到的励磁电流波形基本吻合，验证了三角波激励下磁路模型的准确性。

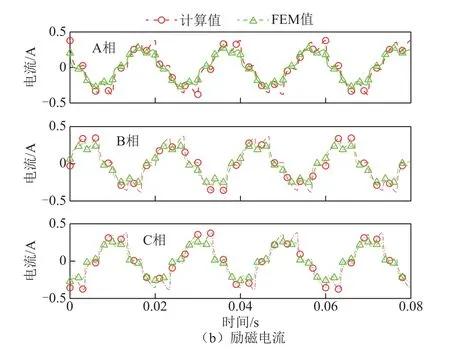
图12 三相三角波激励下计算值与仿真值结果对比 Fig.12 Comparison of calculation and simulation results under three-phase triangular excitation

3.2 方波激励

方波激励采用幅值为200V的三相电压激励，磁路模型计算结果与FEM二维等效模型仿真结果对比如图13所示。对比可知，磁路模型计算得到的 励磁电流与二维等效模型仿真得到的励磁电流波形基本吻合，验证了方波激励下磁路模型的准确性。

图13 三相方波激励下计算值与仿真值结果对比 Fig.13 Comparison of calculation and simulation results under three-phase square excitation

4 试验验证

建立试验平台如图14所示，试验用某80kV·A样机参数见表3。主要测量设备为横河DL850示波记录仪、Isoprobe Ⅱ700929（10:1）电压探头、致远ZY-CTS5（10mV/A）电流探头，在AB单框与CA单框铁轭处设置10匝测量线圈。试验内容包括单相激励空载试验、三相激励空载试验两部分。

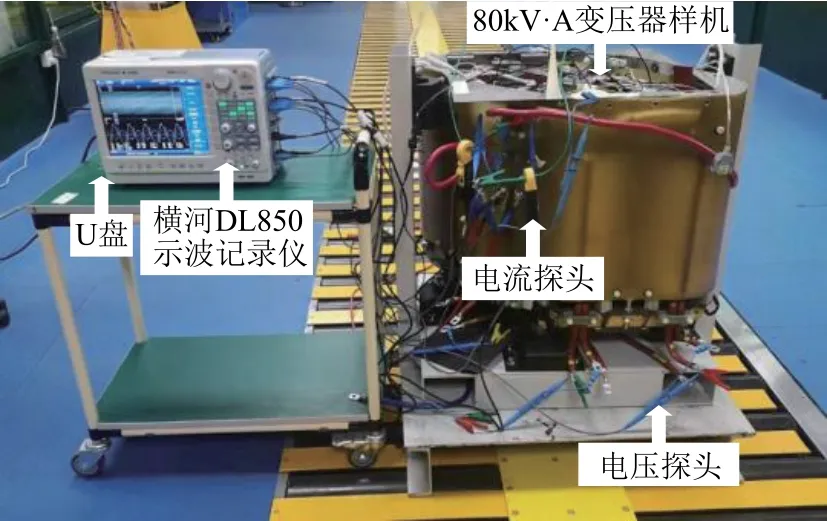
图14 试验平台 Fig.14 Experimental platform

表3 某立体卷铁心变压器样机基本参数 Tab.3 Basic parameters of 3D wound core transformer prototype

4.1 单相激励

单相激励空载试验原理如图15所示。图中Ap、Bp、Cp表示A、B、C三相的一次绕组，As、Bs、Cs表示二次绕组，UPA表示单相电压激励。单相额定电压激励下立体卷铁心变压器试验值与非线性磁路模型计算值、FEM二维等效模型仿真值对比如图16所示，具体数值对比见表4，表中磁通密度幅值，对于计算值是指磁路分析法中磁路等效截面平均磁通密度的幅值；对于试验值是指铁心截面平均磁通密度的幅值；对于仿真值是指FEM三维或二维等效模型中铁心截面平均磁通密度的幅值。对比试验值可知，在单相额定电压激励下，非线性磁路模型单框铁心的磁通密度幅值相对误差不大于0.29%，励 磁电流幅值相对误差不大于0.46%；FEM二维等效模型单框铁心的磁通密度幅值相对误差不大于0.41%，励磁电流幅值相对误差不大于0.31%。

图15 单相激励空载试验原理图 Fig.15 Schematic diagram of no-load experiment under single-phase excitation

图16 单相激励下试验值与计算值、仿真值结果对比 Fig.16 Comparison of experimental values with calculation and simulation values under single-phase excitation

表4 单相激励下试验值与计算值、仿真值结果对比 Tab. 4 Comparison of experimental values with calculation and simulation values under single-phase excitation

4.2 三相激励

三相激励空载试验原理如图17所示。图中UPA、UPB、UPC表示三相额定电压激励。

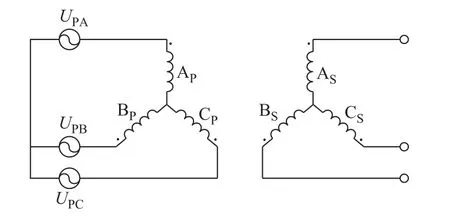
图17 三相激励空载试验原理图 Fig.17 Schematic diagram of no-load experiment under three-phase excitation

三相额定电压激励下立体卷铁心变压器试验值与非线性磁路模型计算值、FEM二维等效模型仿真值对比如图18所示，具体数值对比见表5，表中磁密幅值的定义同表4。

图18 三相激励下试验值与计算值、仿真值结果对比 Fig.18 Comparison of experimental values with calculation and simulation values under three-phase excitation

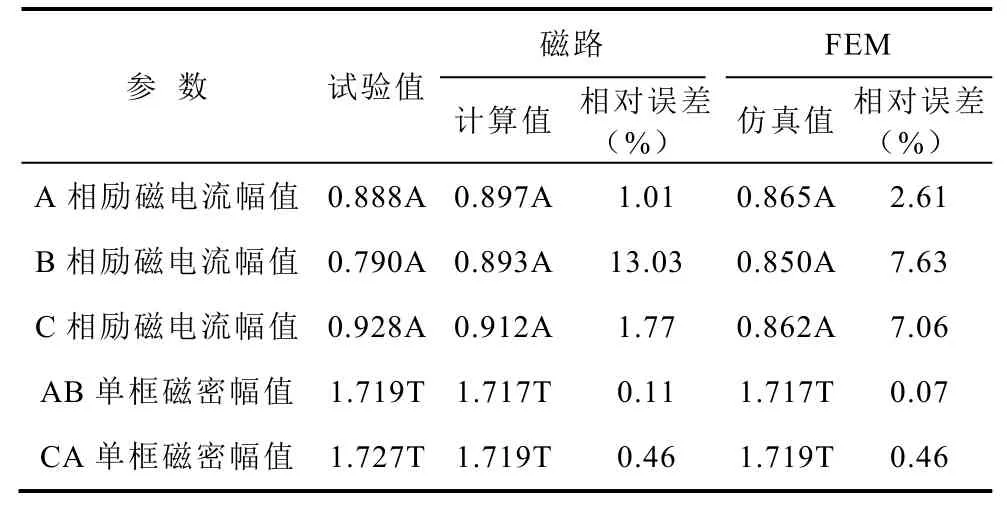
表5 三相激励下试验值与计算值、仿真值结果对比 Tab. 5 Comparison of experimental values with calculation and simulation values under three-phase excitation

与试验值对比，在三相额定电压激励下，非线性磁路模型单框铁心的磁通密度幅值相对误差不大于0.46%，各相励磁电流幅值相对误差不大于13.03%；FEM二维等效模型单框铁心的磁通密度幅值相对误差不大于0.46%，各相励磁电流幅值相对误差不大于7.63%。

以上结果验证了本文建立的非线性磁路模型、FEM二维等效模型的准确性。

4.3 磁滞特性对计算结果的影响

针对本文变压器样机案例，考虑磁滞特性前后的励磁电流及各单框磁通密度FEM仿真结果如图19所示，图20是考虑磁滞特性前后的励磁电流仿真值与试验值幅频特性对比，具体数值对比见表6。

图19 磁滞材料与无磁滞材料二维等效模型 仿真结果对比 Fig.19 Comparison of simulation results of 2D equivalent model between hysteresis and non-hysteresis materials

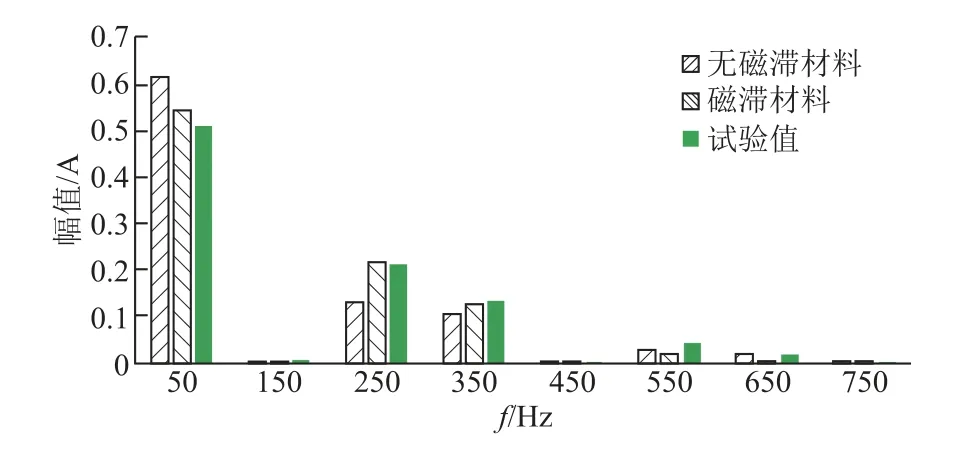
图20 励磁电流谐波频谱 Fig.20 Harmonic spectrum of excitation current

表6 磁滞材料与无磁滞材料二维等效模型仿真与 试验结果对比 Tab.6 Comparison of experimental values with simulation values of 2D equivalent model using hysteresis and non-hysteresis materials

对比可知未使用磁滞材料的FEM仿真所得到的励磁电流波形在幅值点所在轴线左右对称，这与实际励磁电流波形不吻合。考虑铁心磁滞特性前后单框磁通密度幅值仿真值与试验值相对误差不大于0.28%，但励磁电流5次谐波幅值仿真值与试验值相对误差由37.70%下降至1.03%。

4.4 不同电压激励下零序三次谐波对磁密幅值的影响

基于非线性磁路模型，在图17所示三相激励空载试验原理图下，采用不同的电压激励，计算数据汇总见表7，试验数据汇总见表8，不同电压激励下的单框磁通密度幅值与心柱平均磁通密度幅值比值如图21所示，磁通密度谐波含有率如图22所示。

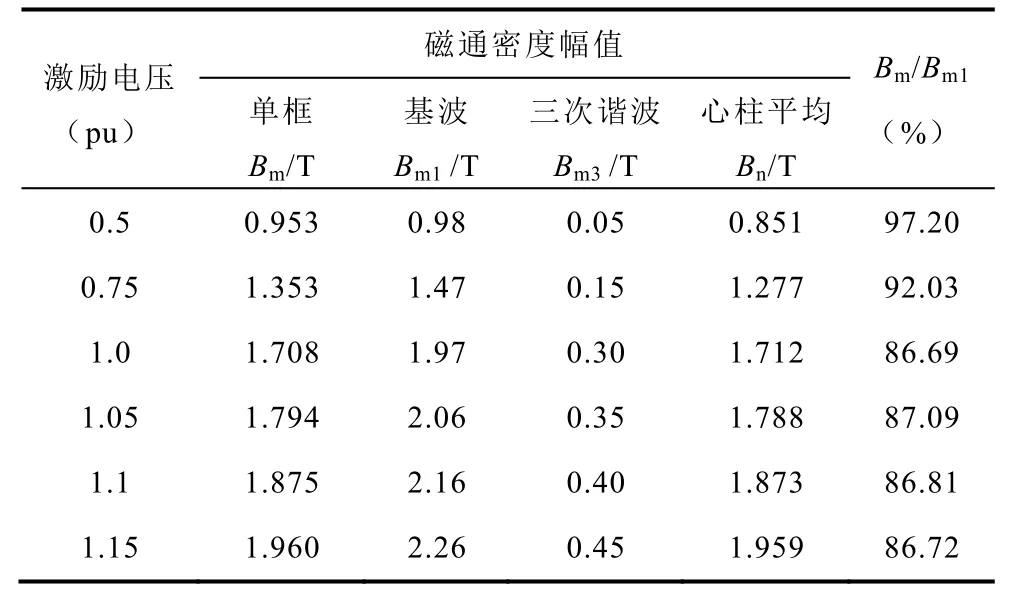
表7 不同电压激励下非线性磁路模型计算结果 Tab.7 Calculation results of nonlinear magnetic circuit model under different voltage excitation

表8 不同电压激励下试验结果 Tab.8 Experimental results under different voltage excitation

对比非线性磁路模型计算数据与试验数据可知，铁心从不饱和状态进入饱和状态的过程中，单框磁通密度幅值与心柱平均磁通密度幅值的比值趋近于1，单框三次谐波磁通密度幅值与含有率逐渐增加，单框磁通密度幅值与基波磁通密度幅值之比Bm/Bm1逐渐减小。在额定电压激励时非线性磁路模型计算的Bm/Bm1为86.69%，试验值计算的Bm/Bm1为87.69%，二者相差1.0%，Bm/Bm1趋近于86.6%，与 文献[2]结论相同，同时也验证了本文非线性磁路模型的准确性。

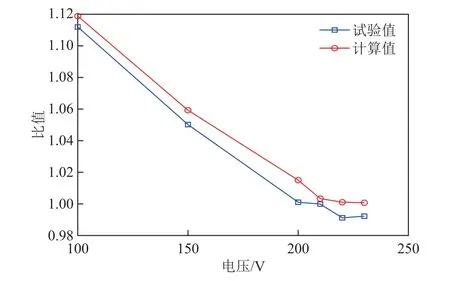
图21 单框磁通密度幅值与心柱平均磁通密度幅值比值 Fig.21 Ratio of single frame magnetic density amplitude to core column average magnetic density amplitude

5 结论

1）本文基于J-A磁滞模型建立了立体卷铁心变压器非线性磁路模型，开展了三角波、方波激励下立体卷铁心变压器的空载特性分析。

2）建立了立体卷铁心变压器FEM二维等效模型，相比三维FEM模型，可以缩短96.66%的仿真时间，减少92.93%的内存占用空间。

3）考虑磁滞特性前后，单框磁通密度幅值与试验值相对误差不大于0.28%，但励磁电流5次谐波幅值与试验值相对误差由37.70%下降至1.03%。可见磁滞特性对励磁电流5次谐波幅值影响较大。

4）对比单相与三相额定电压激励空载工况下磁路模型计算值、FEM二维等效模型仿真值与试验值，验证了本文建立的非线性磁路模型、FEM二维等效模型的准确性。

5）立体卷铁心的三个铁心框磁路相对独立，铁心饱和时，由于三次零序磁通的存在，单框磁通密度幅值接近基波磁通密度幅值的86.6%，单框磁通密度幅值与心柱平均磁通密度幅值的比值趋近于1。因此，与传统三相三柱叠铁心结构相比，三相立体卷铁心结构的心柱材料利用率相当。

6）本文模型可用于非正弦供电立体卷铁心变压器的铁心工作特性分析，为立体卷铁心变压器在电力电子电能变换领域的应用提供技术支撑，后续拟开展SPWM激励下的立体卷铁心变压器电磁暂态过程与直流偏磁的研究。