多线引入的轨道电路横向连接位置优化计算方法
孙 哲
(中铁工程设计咨询集团有限公司,北京 100055)
1 概述
目前,对于设有轨道电路的电气化复线铁路,主要采用横向连接作为连通牵引回路,平衡上、下行线路牵引回流的主要装置[1]。横向连接分为简单和完全两种类型。简单横向连接由空扼流变压器或空心线圈、横向连接线等构成;完全横向连接由高阻抗扼流变压器、横线连接线、中心接地线及吸上线等构成[2]。
在横向连接的工程设计中,现行规范及相关文件[3-6]从频率、间隔长度、连接线距离等多个角度对横向连接的设置进行了规定。其位置设计需考虑大量的约束条件,人工计算的工作量大、准确度不高。为此,杨帆[7]综合考虑了技术规范条件和投资控制,提出了基于回溯法的轨道电路横向连接设置方法,实现了横向连接位置的计算。但此方法未考虑存在并行区段以及某处横线连接上、下行扼流变压器不在同一里程的情况,且采用的回溯法主观性太强,不具备通用性。
现今,我国多个新建铁路项目存在多条联络线或走行线接轨引入正线情况。计算此种情况下的横向连接位置时,需同时考虑正线、引入线横向连接的设置,进一步增加了横向连接位置工程计算复杂度。为此,提出一种考虑多线引入情况的横向连接位置数学模型,并采用基于多目标粒子群的优化方法,综合考虑投资成本及回流性能,以实现此种情况下横向连接位置优化计算。
2 多目标优化问题相关概念
在实际优化问题中,存在着大量具有多个目标函数的情况。解决此类问题,一般可通过线性加权,将其转化为单一目标函数来求解[8]。然而,各目标函数之间往往相互冲突且属于不同量纲,直接线性加权的方法鲁棒性较差。为此,许多学者对以求解Pareto最优解集为目的的多目标优化方法进行了研究[9-11]。
2.1 多目标优化问题基本概念
对于一个求最小值的多目标优化问题[12],可用如下数学表达式表述
miny=f(x)=[f1(x),f2(x),…,fm(x)]

(1)
式中,x=(x1,x2,…,xn)∈Rn为由n个变量组成的决策向量;y=(y1,y2,…,ym)∈Rm为由m个目标函数构成的向量;gk(x)(k=1,2,…,p)与hl(x)(k=1,2,…,q)分别表示需满足的p个不等式约束和q个等式约束。
以求解最小值的两目标优化问题为例,若x1、x2为可行域中的两个解向量,则当且仅当满足如下条件时,称x1支配x2,记做x1x2。
(2)


图1 支配与Pareto前沿
2.2 基于拥挤距离的多目标粒子群
粒子群算法(PSO)是一种基于群体智能的进化式算法,它通过粒子速度和位置更新,迭代出种群历史最优和全局最优,具有收敛速度快、方便计算机实现等特点[13]。
多目标粒子群算法(MOPSO)将PSO的基本原理应用于多目标问题中,通过构造个体历史Pareto最优集Gbest和种群全局Pareto最优集Pbest,以期求解出分布均匀、最靠近真Pareto前沿的非劣解集[14-16]。在迭代过程中,通过拥挤度排序[17-18],找出Gbest、Pbest中稀疏度最大的解作为个体最优解gbest和全局最优解pbest,以实现解的不断优化,算法流程如图2所示。
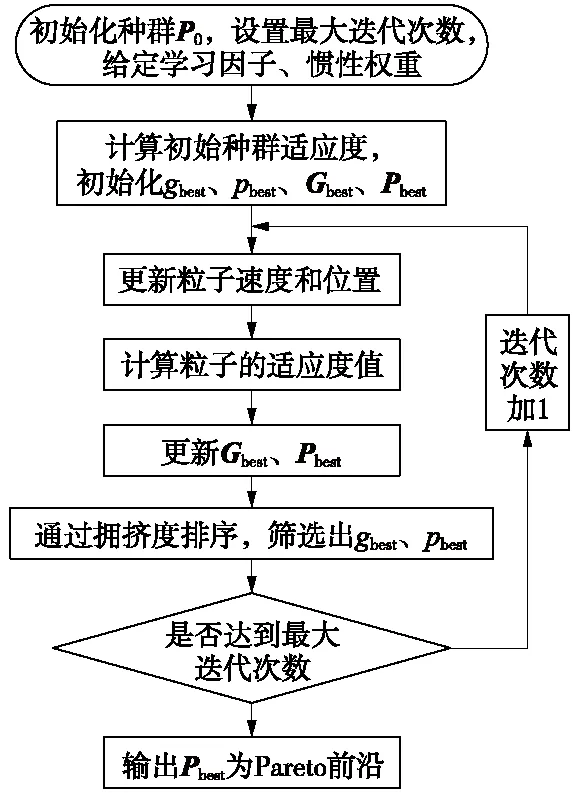
图2 MOPSO算法原理
3 横线连接位置优化问题数学描述
3.1 横向连接位置模型
(1)正线横向连接位置模型
在实际工程应用中,简单、完全横向连接的基本构件均为一对扼流变压器和一条横向连接线。因此,若某条铁路正线设置nz个横向连接,则各个横向连接里程由小到大依次构成nz维向量Hz,表示为

(3)

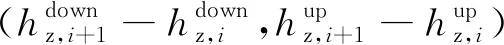
(4)

由式(3)、式(4)可得,正线第i对横向连接的里程可描述为
(5)
(2)引入线横向连接位置模型
对于工程中存在联络线、走行线等引入线的情况,因引入线会通过正线上的接轨点接入正线,则应建立引入线横向连接位置模型,并与正线横向连接位置统筹考虑。

(6)

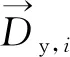

(7)
则引入线上第i对横向连接的里程均可由同方向之前横向连接之间的距离描述,即

(8)

(9)
(10)
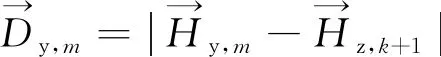
(11)
3.2 约束条件
ZPW-2000A及ZPW-2000R轨道电路工程设计说明中对横向连接的设计位置进行了规定,将其数学描述如下。
(1)相邻横向连接间距约束
根据规范,相邻两个横向连接应至少有一个为完全横向连接,且横向连接设置间隔应满足接触网回流线的间隔要求,则对于同方向相邻横向连接均为完全横向连接的情况,应满足
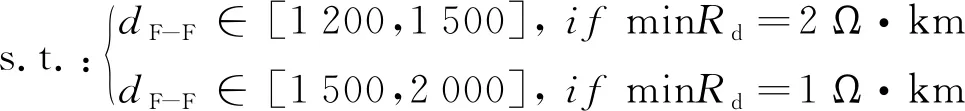
(12)
式中,dF-F为线路连续两个横向连接均完全横向连接时,其同方向的两个扼流变压器的间距;minRd为线路最低道床电阻。
对于线路上某一简单横向连接,由于两处相邻完全横向连接间最多可设置1处简单横向连接,且简单横向连接与完全横向连接间的距离不小于1 000 m,则有

(13)
同时,若minRd=2 Ω·km,满足
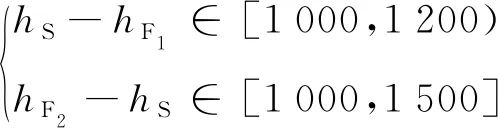
(14)
若minRd=1 Ω·km,满足


(15)
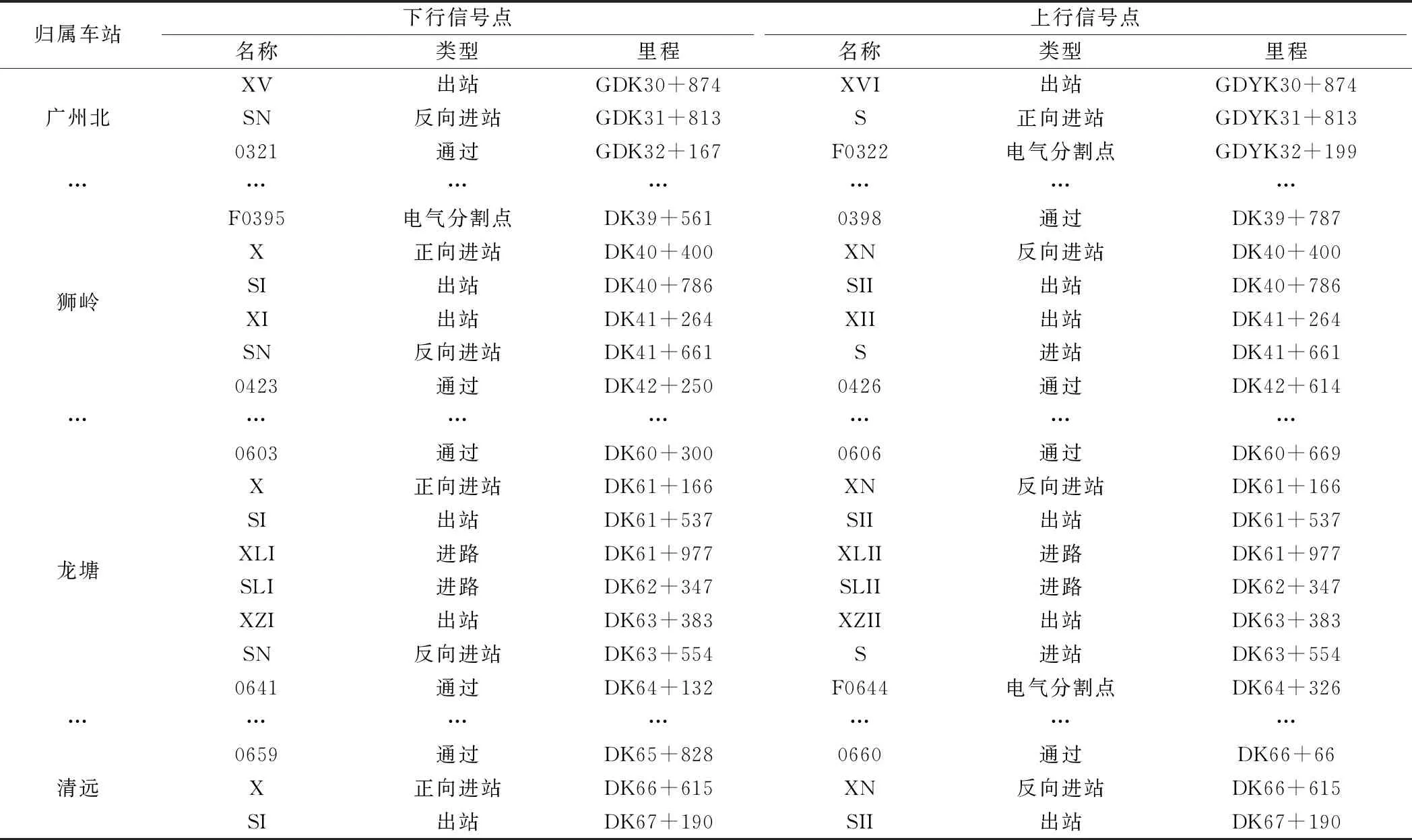
式中,hS、hF1、hF2分别为简单横向连接及其相邻两个完全横向连接同方向上扼流变压器的位置,且hF1 同时,横向连接线不应超过100 m,则有 (16) 式中,φH为同一处横向连接线允许最大里程差,可适当缩小取值,一般取φH=50 m。 (2)补偿电容、调谐单元距离约束 对于正线或引入线上某一处横向连接的扼流变压器,设其所在轨道电路区段有m个补偿电容、2个空心线圈,且里程从小到大依次为 K1,C1,C2,…,Cm,K2 (17) 若该扼流变压器与机械空心线圈处于同一位置,则可利用该空心线圈处的扼流变压器,无需新设,并满足:hi=K1或hi=K2,hi为该扼流变压器的位置。 否则,需新设扼流变压器,且新设扼流变压器相对于补偿电容的距离不应小于10 m、相对于空心线圈的距离不应小于50 m,满足 (18) 式中,φC、φK分别为考虑施工误差而设置的横向连接扼流变压器相对于补偿电容、空心线圈的余量。 (3)频率条件约束 相邻两个横向连接不能接入同一轨道电路区段,即满足 st:hi+1-hi≥lhi (19) 式中,hi、hi+1为相邻两处横向连接同方向线路上扼流变压器的位置;lhi为hi位置处扼流变压器所在轨道电路的长度。 (4)牵引所亭回流线约束 对于距离牵引供电专业牵引所亭位置最近的一组完全横向连接,根据供电专业相应要求,其扼流变压器应设于牵引变电所亭附近一定范围内,即满足 (20) 在满足上述约束条件下,目标函数应考虑工程的经济性、可实施性及可靠性,为此,将目标函数可设置成如下几类。 (1)工程总投资预算应尽可能低 根据式(3)~式(11),则有 (21) 对于正线或引入线上任一处完全横向连接,若两端均需增设扼流变压器和吸上线,则其预算Bi可描述为 (22) 式中,Pe为扼流变压器的单价;le为两端空扼流变压器连接电缆的长度;Pl为连接电缆单位长度预算;Pg为接地预算;δ为线路间距,一般取5 m。 若一端满足设于机械绝缘节空心线圈处,则其预算Bi可描述为 (23) 若两端均满足设于机械绝缘节空心线圈处,则其预算Bi可描述为 (24) 对于处于牵引变电所亭最近的完全横向连接,还应考虑回流线的预算,此时Bi可描述为 (25) 式中,PS为单位长度回流线预算;lS为此处应设回流线长度,此处仅考虑牵引变电所亭与横向连接的相对里程差为回流线长度;S为牵引变电所亭的位置。 对于正线或引入线上任一组简单横向连接,因无需接地处理,则其预算Bi可以描述为 (26) 特别地,对于单线桥梁地段,上述横向连接线长度可设置为0。 (2)连接牵引所亭的回流线的线缆长度尽可能短,使线缆电阻尽量小,线路具备良好的回流性能。即满足 (27) 在工程设计中,正线上第一个和最后一个横线连接位置是可以提前确定的,若两者间距为Lz,且正线所有完全、简单横向连接的个数分别为nz,F、nz,S(nz,F,nz,S∈N),则Lz、nz,F、nz,S之间满足 Lz=(nz,F-nz,S-1)·dF-F+nz,S·dF2-F1 (28) 由此可得 (29) 联合不等式(12)、式(13),进一步可得 (30) 例如:Lz=20 km,minRd=2 Ω·km,若nz,S=0,则nz,F∈(14.1,17.9],即nz,F取值可以为15,16,17;若nz,S=1,则nz,F∈(13.13,17.5],即nz,F取值可以为14,15,16,17。 对于引入线,其横向连接设置范围Ly、完全横向连接个数ny,F和简单横向连接个数ny,S同样满足上述关系。为方便描述,将nz,F、ny,F能取到的最小值和最大值依次表示为Mz,1、Mz,2、My,1、My,2。 由于完全横向连接具有更好的回流性,工程中应尽量全部设置为完全横向连接。因此,在求解横向连接Pareto最优位置集Gbest的过程中,可以先将nz,S、ny,S设置为0,求解此情况下的Pareto最优位置集Gbest。若此时Gbest=∅,则将nz,S的个数依次加1,直到Gbest≠∅。 同时,引入线横向连接的位置依赖于正线接轨点横向连接的位置,因此,可先对正线横向连接位置进行优化,以正线横向连接Pareto最优化位置集Gz,best中每个非劣解的接轨点附近横向连接位置来确定引入线横向连接范围,再依次对引入线横向连接位置进行优化。 以正线的横向连接优化过程为例,算法具体步骤如下。 Step1:确定正线横向连接布置长度Lz及横向连接范围内各补偿电容、电气绝缘节空心线圈、进出站信号机处机械绝缘节、正线股道分割点处绝缘节、各牵引变电所亭里程。 Step2:令nz,S=0,根据式(28)确定Mz,1、Mz,2,并令nz,F=Mz,1。 Step3:根据式(1)~式(4)、式(10)~式(18),初始化本次寻优的正线横向连接位置种群Pz,0。之后根据式(19)~式(24),采用MOPSO求解此条件下正线横向连接Pareto位置集Gz,best,并将Gz,best非支配更新至正线横线连接历史Pareto位置集Hz,best。 Step4:令nz,F=nz,F+1,重复Step3,直至nz,F=Mz,2。 Step5:此时,若Hz,best=∅,则令nz,S=nz,S+1,重复Step2~Step3,直至Hz,best≠∅。 Step6:输出正线横线连接历史Pareto位置集Hz,best。 对正线、引入线横向连接位置依次进行MOPSO优化后,可以得到全线Pareto最优位置集Gbest,再对其进行稀疏度排序,得到最终横向连接位置最优解。 根据本文提出算法,采用Python语言编写出基于MOPSO的横向连接位置优化程序,并以新建广清城际铁路区间横线连接设计为例,对所提算法的有效性进行验证。 广清城际铁路共有1条正线和1条走行线,正线全长38.126 km,设广州北、石陂、狮岭、银盏、龙塘、清远6站,其中,石陂、银盏为无配线站;动车走行线全长3.716 km,并在龙塘站DK139+45.37处与正线接轨[19]。正线、引入线涉及本算法的部分信号点数据如表1、表2所示。 表1 广清城际铁路正线信号点数据 表2 广清城际铁路动车走行线信号点数据 该线路区间仅有1处设有回流线的牵引变电所,位于DK64+557处。同时,全线共有8处断链位置,如表3所示。 表3 广清城际铁路全线断链位置 将上述数据输入本算法程序,并令Pl=10,PS=25,Pe=5 000,Pg=500[20]。经0.48 h算法收敛后,求出的全线横向连接Pareto最优位置集存在4个最优粒子,如图3所示。 图3 广清城际全线横向连接Pareto最优位置粒子 各粒子正线、引入线中简单、完全横向连接个数如图4所示。 图4 Pareto最优粒子中横向连接个数情况 将a1、a2、a3、a4进行稀疏度排序后,可得出粒子a2为最优解。 最优解a2中,正线包含28处完全横向连接,其中,5处利用站内机械绝缘节处扼流变压器,其余23处新设;引入线包含2处完全横向连接、1处简单横向连接,完全横向连接全部利用站内机械绝缘节处扼流变压器。因篇幅有限,此处仅列出a2中动车走行线及龙塘至清远正线区间横向连接位置,如表4所示。 表4 最优解中部分横向连接位置 将a2中各个横向连接位置依次进行检算,结果表明,本算法计算出的横向连接位置完全满足工程设计规范要求。同时,本算法运行时间约为0.5 h,依照工程设计经验,若采用人工计算方式,将至少需要5 h,能够提升设计效率近10倍。 通过构建多线引入情况下的轨道电路横向连接位置模型,将横向连接的工程计算问题转化为了多目标数学优化问题,并基于MOPSO提出考虑多线引入情况的横向连接位置优化计算方法。为验证算法的有效性,采用Python语言编写了算法程序,并选取广清城际铁路正线及走行线数据对本算法进行了验证,结果表明,本算法的计算结果完全满足工程设计要求,并将设计效率提升近10倍。因此,本文算法能够应用于轨道电路横向连接工程设计。



3.3 目标函数

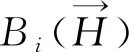




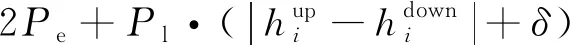


4 横向连接位置优化算法
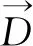
4.1 算法总体思路
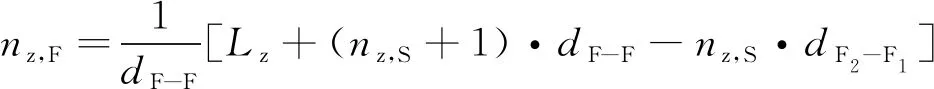
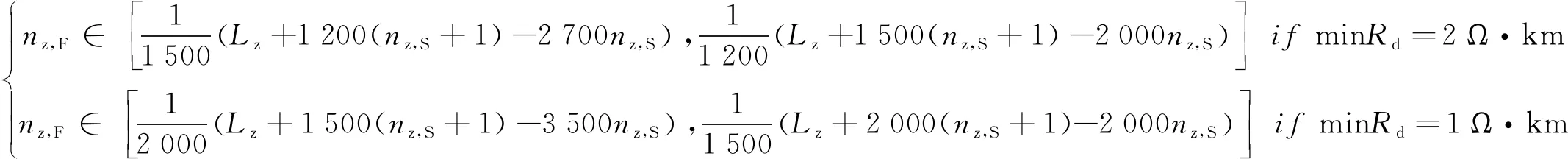
4.2 算例验证





5 结论

