地下水分布对桩体压力影响数值模拟研究

姚 兵，万 涛，陈春汉，黄传胜

（1.江西圳发建设集团有限公司，江西 南昌 330002；3.东华理工大学 土木与建筑工程学院，江西 南昌 330013）

0 引言

钻孔灌注桩是国际上应用十分普遍的一种桩基形式，我国从 20 世纪 60 年代开始首先在公路桥上应用，而后发展到工民建、铁路系统等部门广泛使用［1］。地下水在建筑的过程中起到不可或缺的作用，在施工及日后的使用过程中，需始终保持对地下水有效的控制，确保施工质量、进度甚至人员生命的安全。随着岩土工程勘察人员对于水文地质条件研究的逐步深入，地下水对工程建设所产生的危害也逐渐受到了普遍关注。现已有学者对基坑地下水开展了诸多研究。孟玉山等［2］通过结合张家口赛区奥运村建设工程，探讨了地下水对基坑的影响，提出了截水法、降水法、排水法等治理方案；张建忠等［3］对基坑渗漏情况进行分析，得出了基坑止水帷幕失效的原因及机理，并通过改进后的三孔注浆法和坑内止水帷幕等施工方法对基坑止水帷幕进行了有效修复；张飞等［4］利用 PLAXIS 建立内撑式基坑的承压水抗突涌分析模型，分析坑底隔水层的实际应力应变状态，发现数值分析方法可以较好地反应内撑式基坑抗突涌稳定性与围护墙及土体变形性状的相互影响及计算结果更为符合工程实际；唐世栋等［5］通过对桩基施工过程中实测资料的分析，探讨了沉桩时单桩周围土中产生的超孔隙水压力的大小、分布及影响范围，并与理论解进行了对比，得出了在平面应变条件下岩土任意面上的抗剪强度通式、破坏面位置与强度准则的一般关系、破坏时中主应力与大小主应力的关系和平面应变状态下的统一强度准则。

以上研究多针对于地下水的影响因素以及治理方案，对地下水作用于桩体的机理研究较少。基于此，本文结合实际工程，利用 FLAC3D软件对基坑钻孔灌注桩在不同工况下的地下水分布桩体压力分布规律开展数值模拟研究，为基坑支护设计提供依据。

1 工程概况

本工程为二层地下室，开挖区深度为 12.6 m，挡土止水方案采用灌注桩+三轴搅拌桩和高压旋喷桩，其中钻孔灌注桩，设计桩体长度H=15.0 m，桩径D=1.0 m，桩身混凝土强度等级为 C35，相应杨氏模量E=3.15×104MPa，泊松比μ=0.167，密度ρ=2.5×103kg/m3。模型详细计算参数如表 1 所示。本文选用单一均质黏土，如图 1 所示。

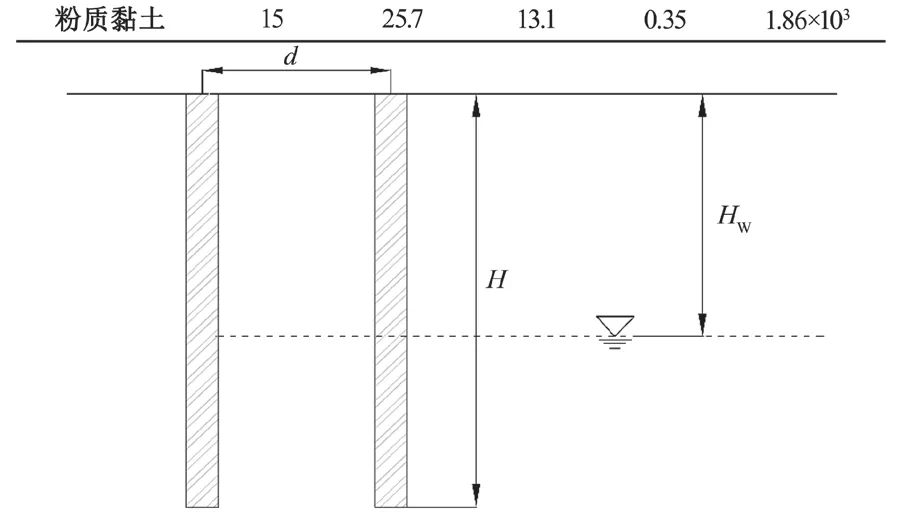
图1 水位分布示意图

表1 模型计算参数取值表

2 试验方案

考虑桩及周围土体的对称性，本文选取实际情况中的一半进行模拟。桩身和土体都采用实体单元，土体采用摩尔-库仑本构模型。桩体采用弹性本构模型，设置桩周土的几何尺寸径向为桩径的 10 倍，以减小模型边界效应，深度取为两倍桩长，整个模型尺寸为 20.0 m×10.0 m×30.0 m。桩土模型网格划分如图 2～4 所示。

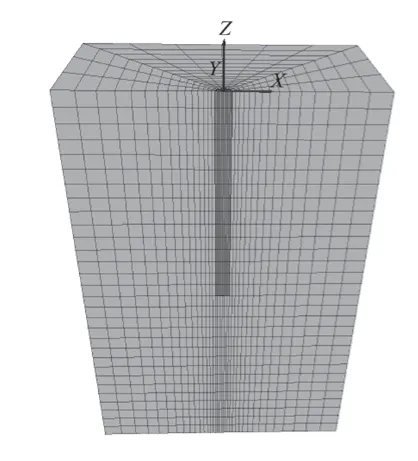
图2 单桩网格划分图

轴向网格划分时考虑水平受荷桩的变形主要发生在受力处的周边，故由中心向外辐射网格由密到疏。土体两侧边界分别约束其水平位移，对土体底部边界同时施加水平和竖向约束。桩土接触面采用 Interface 来传递土体对桩的横向荷载，能够更好地模拟两个接触的表面发生的错动、滑移和分离，模型接触面如图 5 所示。钻孔灌注桩的桩土界面比较粗糙，接触面上的摩擦特性较好，接触面上的c、φ值取与桩相邻土层的c、φ值的 0.8 倍；法向刚度kn和剪切刚度ks取周围“最硬”相邻区域等效刚度的 10 倍［6］，计算公式如式（1）所示。

图3 隔桩网格划分图

图4 连续墙网格划分图

图5 模型接触面示意图

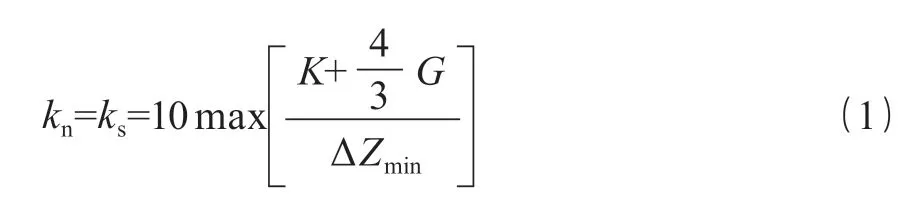
式中：K表示体积模量，Pa；G表示剪切模量，Pa；ΔZmin表示接触面法向方向上连接区域上最小尺寸，m。

在桩与水的作用分析中，先建立土体模型及桩体，设置水位面和桩土间的接触面，进而将桩体移入土体中，并施加相应的边界约束，通过计算先得出重力荷载下的初始应力场。其中计算采用无渗流模式，使用 water table 命令设置水位面，并在水上设置干密度 1.75×103kg·m-3，水下设置饱和密度 1.86×103kg·m-3。再将得到的应力场和重力荷载共同施加于原始有限差分模型，可以得到模型整体应力分布。

3 试验结果与分析

3.1 水位的影响

保持桩长H=15.0 m，分别研究单桩在施加水位面和未施加水位面下桩体单元的 3 个方向的总压力随深度变化情况。沿桩身每隔 1.5 m 取一个数值模拟监测点，共 11 个。桩身单元的 3 个方向的总压力随深度变化的比较结果如图 6 所示，其中标注“app”的结果是施加水位面情况下的压力计算曲线，标注“Noapp”的结果是未施加水位面情况下的压力计算曲线。

图6 不同工况下压力沿桩深分布关系图

由图 6 可知，同种工况下x方向总压力与y方向总压力始终差别不大；两种情况计算的z方向总压力在距桩底最后 3 m 处的结果相差很大，在模型底部单元（标高-15.0 m）的z方向总压力分别为 -324.42 kPa（app）和-268.47 kPa（Noapp），增幅约为 20.8 %；在同一深度，施加水位面比未施加水位面，x方向总压力增大了 50 %，说明水对桩的作用主要体现在水平方向，但由于桩底在水平力作用下，容易发生错动、滑移等，从而使桩体受到更多的竖向压力。

3.2 水位深度的影响

地下水对桩体的影响在水平方向最为明显，保持桩长H=15.0 m，分别研究单桩在不同的地下水位分布比例（Hw/H=0，0.2，0.4，0.6，0.8，1.0）等 6 种工况x方向上总压力分布情况。沿桩身每隔 1.5 m 取一个数值模拟监测点，共 11 个。由图 7 可以看出：相邻的两个Hw/H压力曲线变化发生在较小值的地下水位面处，如Hw/H=0.4 与Hw/H=0.6 的曲线变化点在H=6.0 m（Hw/H=0.4）处，在 0.0 m～6.0 m，两者曲线趋近于相等，在 6.0 m～15.0 m，呈现出两条平行的曲线，取桩体同一深度，可以发现随着水位的下降，x方向上总压力值以 10 % 逐渐降低。

图7 不同 Hw/H 下压力沿桩深分布关系图

3.3 单桩施工、隔桩施工、地下连续墙施工的分析

保持桩长为 15.0 m、地下水位分布比例Hw/H=0 不变，研究单桩施工、隔桩施工（d/D=2.0）、等刚度地下连续墙施工 3 种工况下的桩体总压力分布情况。沿桩身或墙身每隔 1.5 m 取一个数值模拟监测点，共 11 个，隔桩施工、地下连续墙对内侧与外侧分别进行监测如图 8 所示，桩身单元的 3 个方向的总压力随深度变化的比较结果如图 9～11 所示。将围护桩等刚度转变成墙来等效模拟运算［7］，由D=1.0 m，d=2.0 m，计算式如式（2）所示。

图8 监测示意图

式中：D为表示围护桩的桩径，m；d为表示桩间净距，m。

由图 9、图 10 可知，隔桩施工时桩间的挤压作用使桩体上部分内侧的压力与外侧的压力产生差异；在桩底，内侧水平方向总压力比外侧水平方向总压力增长了 7.6 %，z方向总压力增长 6 %；对比图 10 与图 11，可以 发现地下连续墙施工内侧与外侧 3 个方向的总压力差异不大，均与隔桩施工外侧、单桩施工相应压力值的差异保持在 1 % 范围内，这说明等刚度地下连续墙施工内部比隔桩施工桩间更能抵抗水平挤压作用。

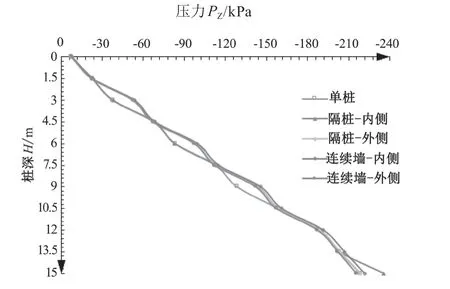
图9 不同施工下 x 方向总压力沿深度分布关系图

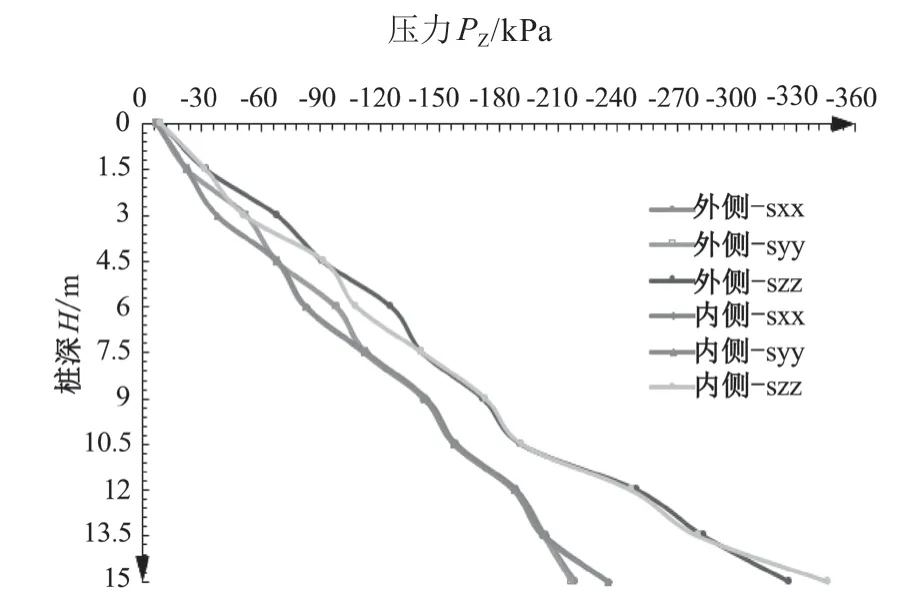
图10 隔桩施工压力沿深度分布关系图

图 11 地下连续墙施工压力沿深度分布关系图

4 结论

1）同种工况下，x方向总压力与y方向总压力在重力荷载作用下近似相等；两种情况计算的z方向总压力在桩体底部单元（标高-15.0 m）的z方向总压力分别为-324.42 kPa（app）和-268.47 kPa（Noapp），增幅约为 20.8 %；在同一深度，施加水位面比未施加水位面，x方向总压力增大了 50 %，这说明地下水对于计算结果的影响非常大，其中水平方向较为明显，竖向则主要体现在桩体底部。

2）相邻的两个Hw/H压力曲线变化发生在较小值的地下水位面处，地下水位面以上两者的压力值趋近于相等，水位面以下呈现出两条平行的曲线，同一深度，随着水位的下降，x方向上总压力值以 10 % 逐渐减少。

3）隔桩施工桩间方土体的挤压作用造成桩体上部分内侧的压力与外侧的压力不同，桩底内侧水平方向总压力比外侧水平方向总压力增长了 7.6 %，z方向总压力增长 6 %；地下连续墙施工内侧与外侧 3 个方向的总压力均与隔桩施工外侧、单桩施工相应压力值的差异保持在 1 % 范围内；等刚度地下连续墙施工相对于隔桩施工桩间更能抵抗水平挤压作用。Q