预制-装配式多键群剪力键力学行为试验研究

石璐，范亮

(重庆交通大学 土木工程学院，重庆，400074)

近年来，钢-混组合结构由于能够充分发挥钢和混凝土两种材料的特性[1]，力学性能好，施工方便，得到了迅速发展，被广泛应用于桥梁、高层建筑等领域。作为钢-混组合结构的重要组成部分，剪力键防止界面处钢梁与混凝土板的滑移和分离。

目前，对现浇组合结构中栓钉连接件的研究已相当充分，针对剪力键的承载力、刚度以及对组合梁力学行为的影响开展了较多的单钉以及群钉试验研究[2-4]。周绪红等[5]发现，群钉效应会导致平均单个栓钉承载力和抗剪刚度显著降低。苏庆田等[6-7]进行了1组单钉和5组不同群钉布置形式的连接件推出试验，得到了群钉布置形式的荷载-滑移曲线以及表达式。Zhang等[8]考虑横向配筋率、剪切连接度、螺栓直径对组合梁剪切特性的影响，提出了纵向双排螺柱的纵向抗剪强度计算公式。

随着装配式组合结构的广泛应用，逐步开展了装配式组合结构的研究，分析了装配式组合结构中剪力键的力学行为影响[9-11]。Wang等[12]考虑了后浇孔形状、加载方式以及浇筑方法的影响，设计了4个现浇推出试件和12个预制推出试件，得到现有的设计公式可以用来计算抗剪栓钉组的抗剪承载力。项贻强等[13]开展了3片装配组合梁与1片现浇组合梁的对比试验，认为在完全抗剪设计时，栓钉布置形式对组合梁的刚度和承载力影响较小。刘沫宇等[14-15]开展了1片2×8.5 m装配式连续组合梁的试验研究，结合数值分析，认为装配集束钉群满足港珠澳大桥中装配组合连续梁桥的设计要求。Shim等[16]研究发现，JSCE、EC-4、Guidelines及AASHTO等规范中均缺乏集束钉群装配式组合结构相关设计条款，表明预制-装配式组合结构亟待深入研究。学者们开展了大量对现浇单钉、钉群以及装配式组合梁的研究，但对于预制-装配式键群力学行为研究较少，特别是多个装配式集束键群间的共同工作性能的研究尚未见报道。考虑到多键群共同工作更接近于装配式组合梁中剪力键的真实受力状态，为了更好地研究装配式键群数量对结构受力的影响，开展了单键群和多键群装配式剪力键对比研究，讨论多键群力学行为及承载力折减效应。

1 单键群与双键群的装配式剪力键推出试验

1.1 试件设计与制作

设计了一组单键群(N1)和一组双键群(N2)栓钉推出试验，每组各3个试件。试件的设计参照了欧洲Eurocode4-2004规范[17]，根据试验的实际要求和条件对试件作部分调整。试件尺寸和试件制作顺序如图1、图2所示，钢梁厚度为9 mm，因先后浇混凝土交界面处为薄弱交界面，故在后浇孔洞两侧设计双层箍筋，并在双层箍筋4个角位置处放置4根竖向φ6.5的HRB335钢筋形成钢筋笼，且混凝土保护层厚度为10 mm，H型钢均为热轧Q235，试件中栓钉采用直径13 mm、长80 mm的ML15，先浇混凝土为C50，后浇混凝土为C60，先后浇混凝土立方体抗压强度试验和弹模试验均按照《普通混凝土力学性能试验方法》(GB/T 50081—2002)[18]进行测试。材性如表1所示。

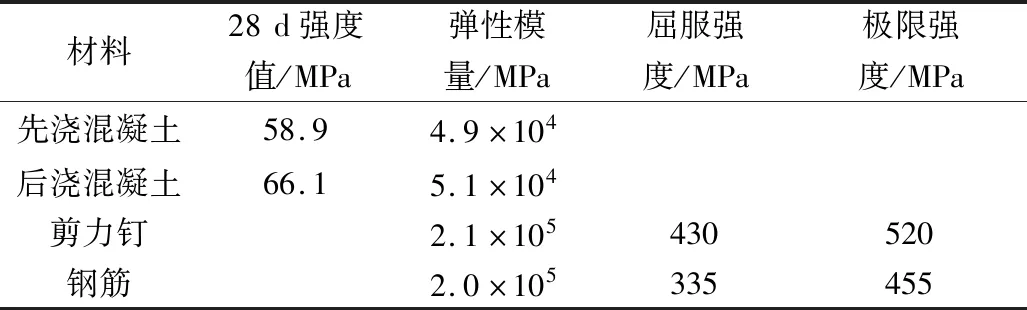
表1 材性参数Table 1 Material parameters

图1 试件尺寸(单位：mm)

图2 试件制作顺序Fig.2 Production sequence of test

1.2 测点布置和加载方案

采用电子位移计测量试件整体位移。采用10 000 kN电液伺服万能试验机进行加载(图3)。

图3 加载及测点布置示意图Fig.3 Schematic diagram of loading and

采用分级加载进行3次弹性加载和3次弹塑性加载，最后进行破坏加载。加载方案如图4所示。

图4 加载方案示意图Fig.4 Schematic diagram of loading

2 预制-装配式群钉剪力键的有限元分析

2.1 建模参数

利用Abaqus建立装配式群钉推出试验的有限元模型，模型本构选择如表2所示。

表2 模型本构Table 2 Constitutive model

加载采用位移加载，混凝土单元本构关系采用文献[19]建议的混凝土本构关系，混凝土单轴受拉、受压应力-应变曲线如图5所示。结合已有研究，装配式栓钉剪力键进入塑性的原因主要是栓钉周边混凝土局部进入塑性，其次是栓钉根部进入屈服甚至剪断，因此，模拟周边混凝土进入塑性以及栓钉弹塑性本构。为了模拟周边混凝土进入塑性，考虑用的是混凝土的损伤本构，因此栓钉采用双折线本构，超过屈服应变后考虑其进入屈服平台，其后栓钉依次进入屈服，在屈服之后栓钉将会通过快速变形模拟失效过程。混凝土损伤模型如图6所示，钢材本构以及材料的应力与塑性应变关系如图7、表3所示。

表3 钢材应力与塑性应变关系Table 3 Relationship between steel stress and plastic strain

图5 混凝土单轴应力-应变曲线Fig.5 Uniaxial stress-strain curve of

图6 混凝土损伤模型

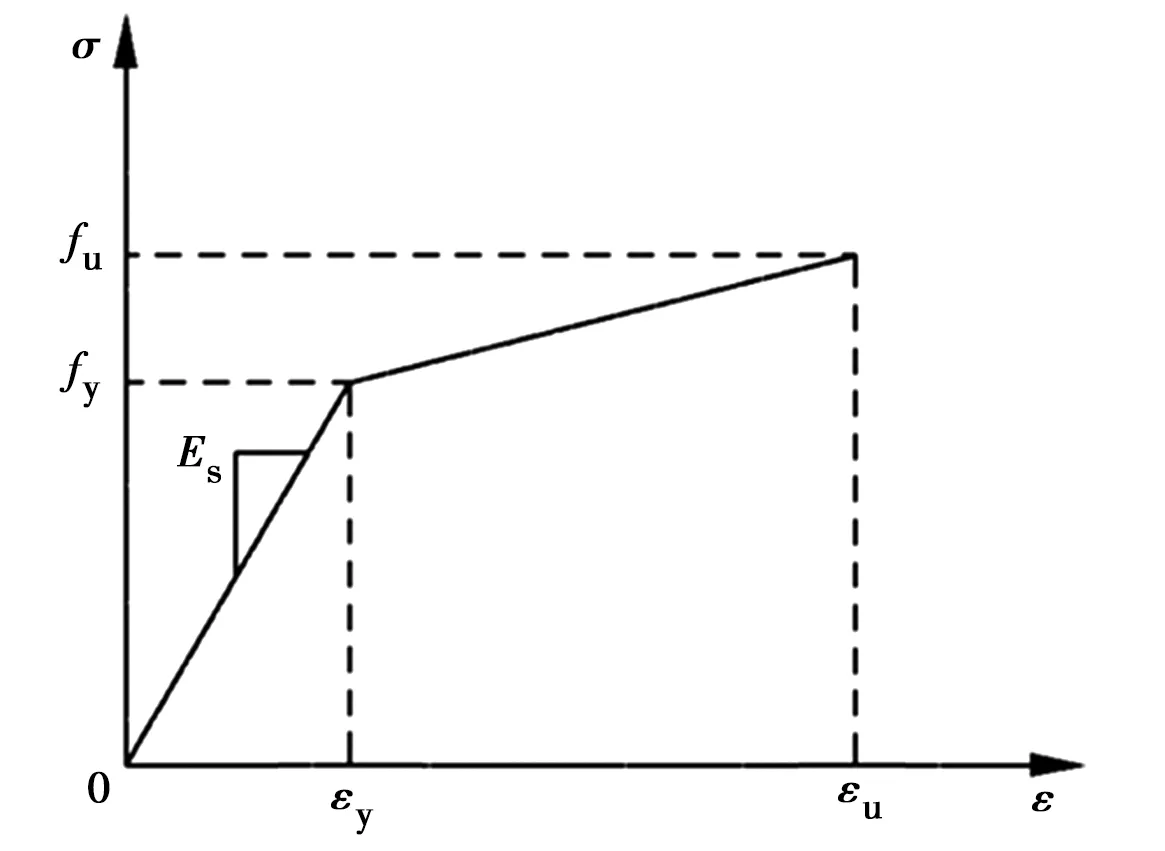
图7 钢材本构关系图Fig.7 Constitutive relation diagram of

2.2 界面接触模拟方法

混凝土与钢梁及栓钉间的界面接触采用硬摩擦模拟，先后浇混凝土的顶面和侧面采用内聚力接触，底面受压采用绑定接触。装配式群钉单键群和双键群试件模型(图8)中包括H型钢、预制混凝土、后浇混凝土以及钢筋骨架。

图8 预制-装配式群钉推出试验构造图(上为N1试件，下为N2试件)Fig.8 Structural drawing of push out test of prefabricated assembled group nails (N1 test piece on the top and N2 test piece on the

2.3 边界条件

为了模拟的真实性，在整个推出试件的下方建立一个完全固结的单元，将试件的混凝土下表面与其上表面建立摩擦接触，如图9所示。

图9 模型边界条件图Fig.9 Model boundary condition

3 推出试验结果及数值模拟

3.1 破坏情况

N1试件加载到60%极限荷载时，先后浇混凝土界面出现缝隙；随后预制混凝土表面开始出现裂缝，紧接着，裂缝沿界面角隅处45°向下扩展；混凝土底部出现竖向裂缝并向上扩展。N2试件的破坏形态略有不同，裂缝首先出现在两个键群之间，随后加载端键群的先后浇混凝土界面出现裂缝并向下延伸，混凝土底部出现与下边缘垂直的竖向裂缝并向上部延伸，两键群之间的预制混凝土呈现横向贯通裂缝(图10(a))。

所有试件破坏时栓钉根部均被剪断(图10(b))，背离加载侧混凝土被压碎，呈半椭圆形(图10(c))。

图10 试件破坏情况示意图Fig.10 Schematic diagram of specimen

对比有限元模拟与试验结果(图11)，有限元模拟中的混凝土损伤基本为受拉损伤，可以反映实际结构中的混凝土开裂现象。在单键群试件中，混凝土板裂缝同样出现在先后浇界面角隅处并向外扩展，在双键群试件中，裂缝出现在两个键群先后浇界面角隅处以及双键群间的预制板处，裂缝的类型及其出现的加载顺序(裂缝出现的顺序为图11中的1、2、3)，与试验基本一致，认为加载过程中开裂现象吻合较好。

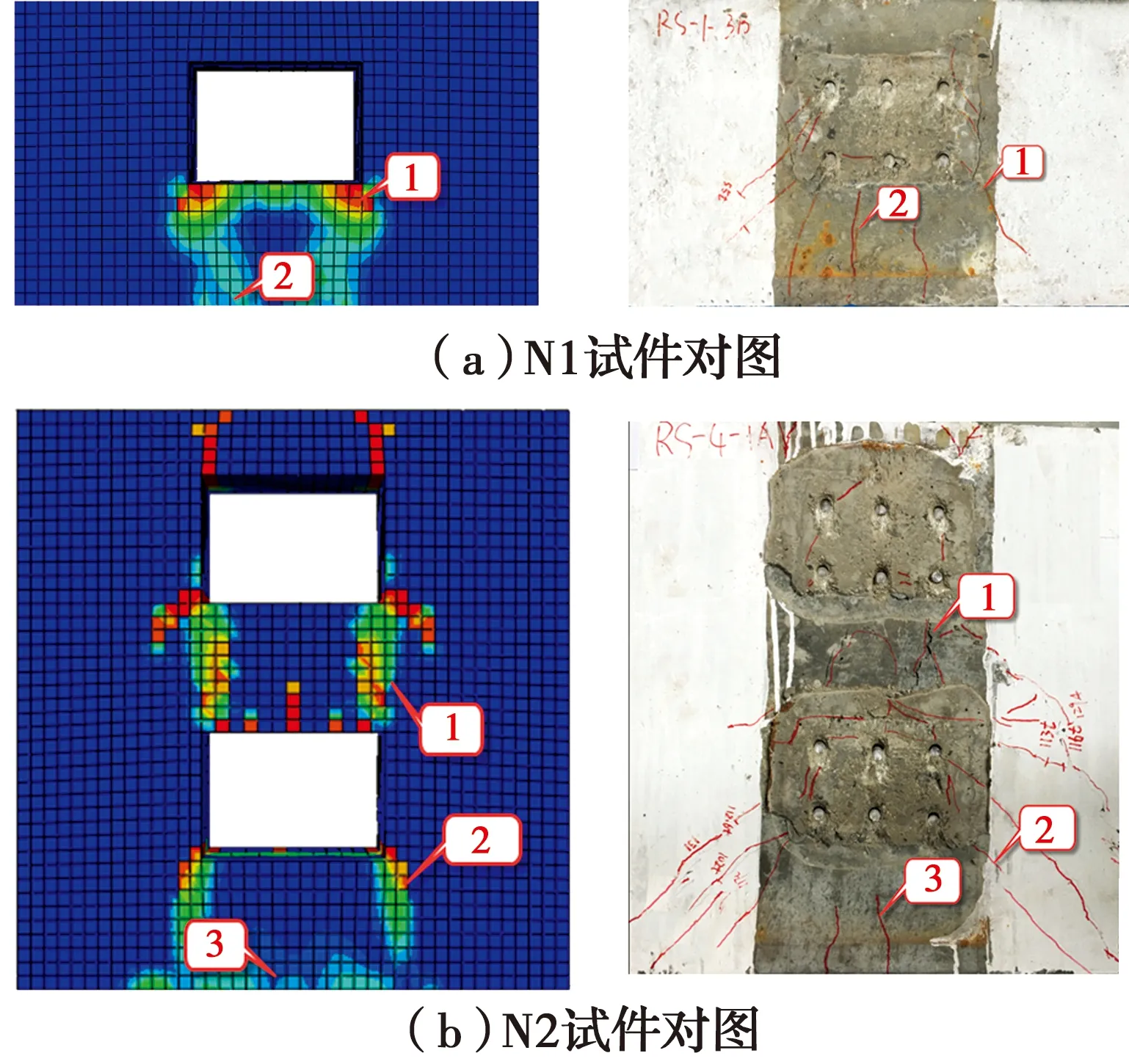
图11 混凝土损伤云图与试验裂缝对比图Fig.11 Comparison of concrete damage nephogram

3.2 荷载-滑移曲线

由图12可知，N1和N2的荷载-滑移曲线趋势大致相同，分为两个阶段：近似的线弹性段和塑性段。在峰值荷载的60%～70%之前为近似的线弹性段，在该阶段整体滑移较小而荷载快速升高；随着荷载的增大，进入塑性段后，试件的整体刚度不断减小，此时混凝土开裂并不断扩展，试件抵抗变形的能力逐渐变弱，试件内部的栓钉逐个进入屈服，随后荷载增长缓慢而滑移不断增大，直至试件破坏。

图12 试验值与模型值荷载-滑移对比图Fig.12 Load-slip comparison diagram of test value

数值模拟与试验实测的荷载-滑移曲线趋势基本一致，数值模拟能够较好地模拟预制-装配式键群剪力键推出试验。

3.3 预制-装配式钉群力学行为分析

表4列出了N1和N2试件实测承载力及平均单键承载力。由表4可知，N1试件单个键群承载力明显高于N2试件。

表4 N1及N2试件试验单个键群承载力统计Table 4 Bearing capacity statistics of single bond group in N1 /N2 test piece

为了进一步研究键群数量对栓钉连接件的力学行为影响，采用上述模型参数及建模方法，模拟3个键群及4个键群的预制-装配式键群剪力键推出试验(图13)(编号为N3、N4)。N3和N4试件的栓钉布置形式及数量与N1、N2一致，钉群数量分别为3个及4个。

图13 各键群模型示意图Fig.13 Schematic diagram of each bond group

各键群的荷载-滑移曲线如图14所示。剪力键的承载力和刚度均与键群数量显著相关：随着键群数量的增加，试件的抗剪承载力和抗剪刚度均随之增长，但单个键群的承载力则随键群数量下降。

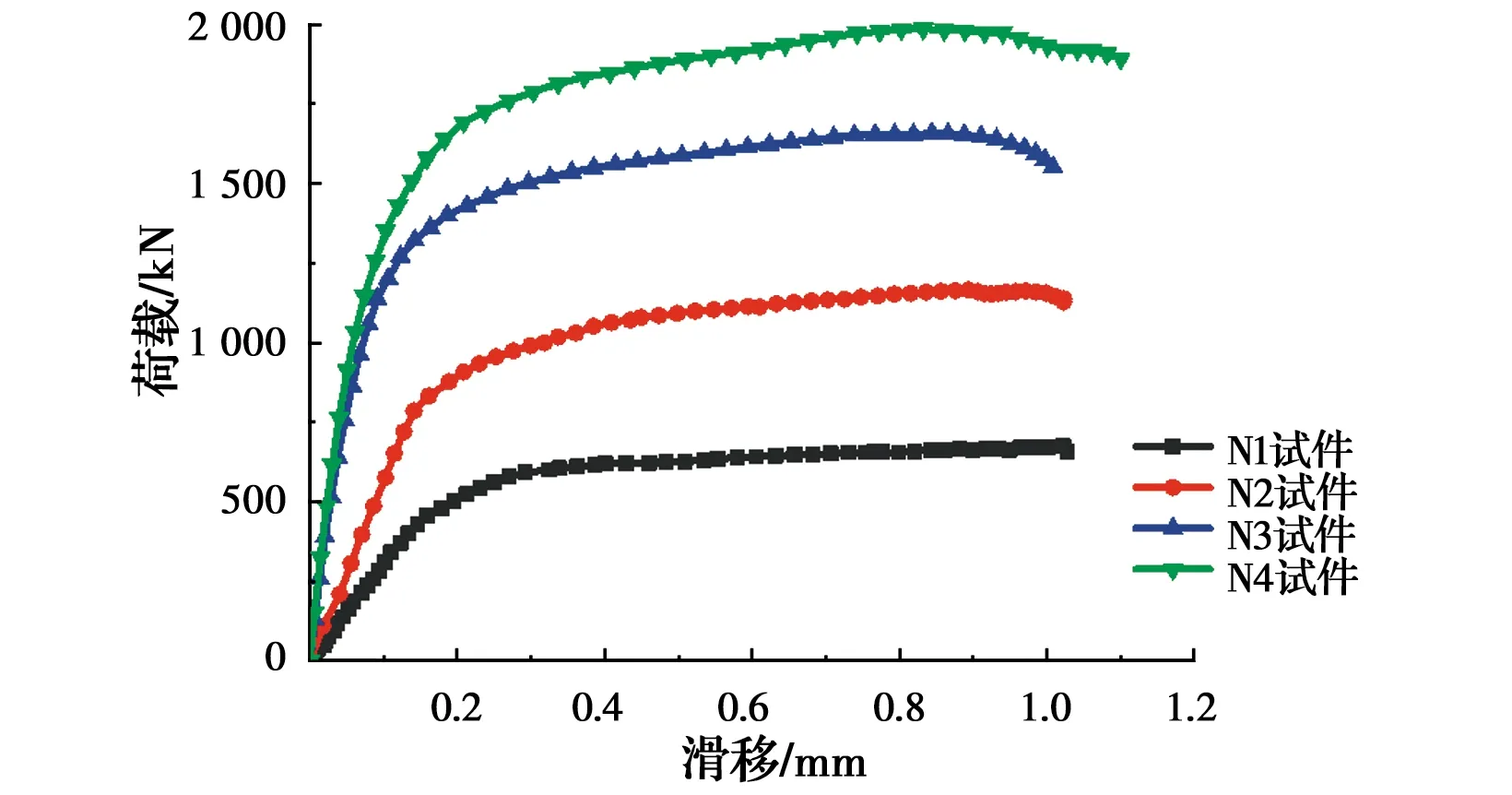
图14 各试件荷载-滑移曲线图Fig.14 Load-slip curve of each test

为了分析剪力键沿剪力方向的受力分布，提取沿试件高度不同位置的钢梁与混凝土间的滑移变形，具体为各个键群中部以及键群与键群中部(图15)(N3、N4试件同N2)。

图15 N2试件滑移测量位置Fig.15 N2 test piece slip measurement

图16 各试件不同荷载下剪力方向的界面滑移Fig.16 Interface slip in shear direction of each specimen

由图16可知，滑移值沿受力方向分布呈现明显的不均匀，下端的滑移大于上端，滑移从下至上基本呈递减趋势，滑移差值最大可达到1.5 mm，界面最小滑移约为最大滑移的67%，表现出明显的不均匀性；随着荷载增加，两端的差值增加，但考虑到总移量的增加，相对不均匀程度减小。考虑到界面滑移变形基本为栓钉的受力变形，其不均匀实际上反映出界面剪力的不均匀，这一现象与多键群试件中单个键群的承载力折减现象有密切关系。

提取各试件中每个钉群同一位置(第2排中间位置)栓钉的剪应力云图，如图17所示，图上数字代表各剪力钉根部剪应力大小，由图17可知，在同个试件中栓钉受力不均匀，呈现出下方大上方小的特点，N1～N4试件中最大栓钉受力相近，但是平均单个栓钉的剪应力分别为290、250、240、210 MPa，随着栓钉群个数的增多，栓钉折减程度也在增大，栓钉受力不均匀会导致承载力的折减。将图17中的数据画成折线图(图18)，可以更为直观的看出各个钉群剪力分布不均匀，从上到下分别为一、二、三、四键群。

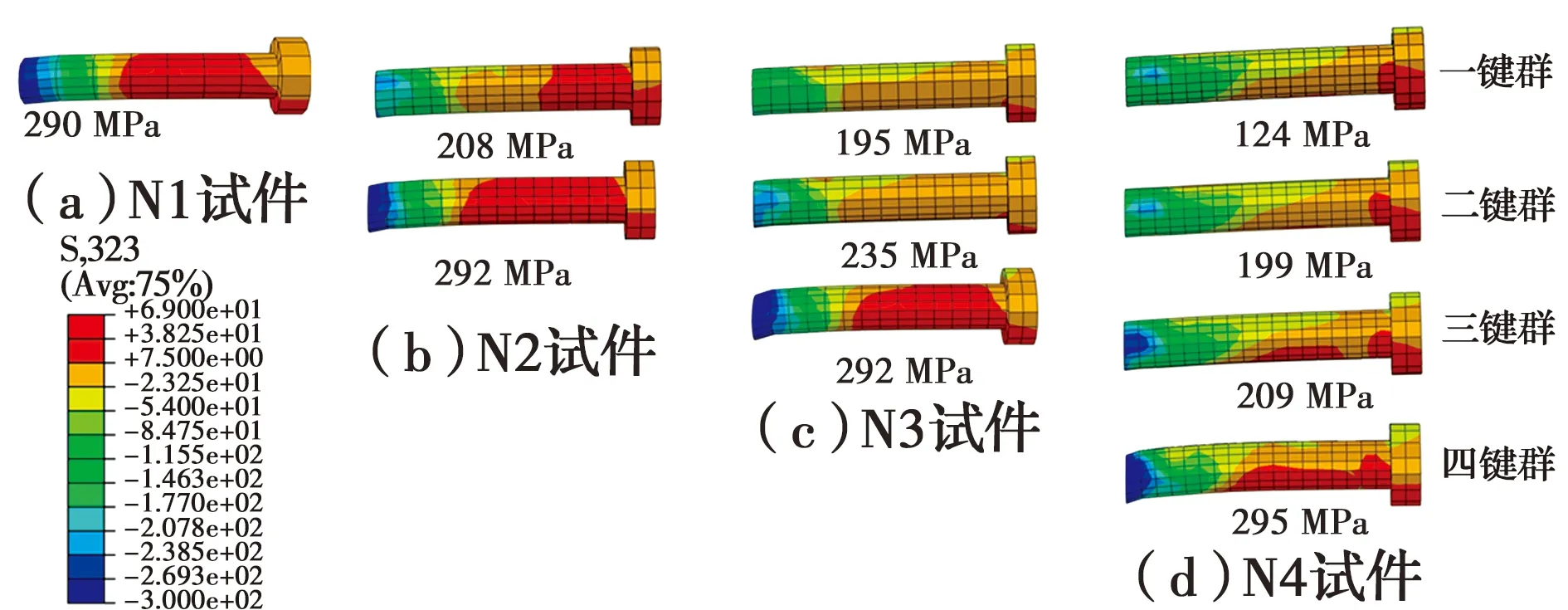
图17 各试件每个钉群同一位置处栓钉应力云图Fig.17 Stress nephogram of stud group at the same

图18 各试件典型栓钉剪应力Fig.18 Typical stud shear stress of each

3.4 多键群承载力折减效应分析

由表5可知，单个键群平均承载力随键群数量增多而减小，N4试件较N1试件承载力折减了28%。分析认为，折减效应是由于沿受力方向各承力构件受力不均匀导致。当单键群试件受力时，单个键群的极限状态即为整个试件的极限状态；当多键群试件受力时，由于键群间的受力不均匀，多个键群不能同步达到其极限状态，此时，多键群试件承载力不再是对应的所有键群的承载力之和，这种现象即导致多键群的承载力折减效应。

表5 各试件计算单个键群承载力统计Table 5 Calculation of bearing capacity of single key group of each test piece

为简化理论推导过程，假设：栓钉剪应力和滑移在弹性阶段成正比，栓钉开始屈服时试件到达极限承载力，如图19所示。根据能量法，能量=力×变形，由于变形不均匀导致受力不均匀，每个试件的最大能量体现了变形不均匀程度。对在n个键群时，折减系数为

(1)

图19 剪力与滑移的关系Fig.19 Relationship between shear and

将图18中的数值带入式(1)，计算出的N2、N3、N4试件承载力折减系数为0.86、0.82、0.72，与表5比较可以认为，能量法面积折减可以较好地描述承载力折减的机理，表明键群间受力的不均匀性是多键群承载力折减效应的原因，并可根据其不均匀性计算出承载力折减系数。

承载力折减系数与键群数量有关，键群数量越多，承载力折减越大，以ξ为承载力折减系数，由计算得到，当n≥2时

ξ=0.359 4/n+0.652 8

(2)

式中：n为键群个数。

4 结论

1)单键群和双键群试件的荷载-滑移曲线趋势无明显差异，呈现出近似两段式：近似线弹性段和塑性段。破坏形态有所不同，且双键群试件的破坏程度大于单键群试件。

2)试件加载过程中，滑移从上至下逐渐递增，下端键群滑移值最大。承载力折减效应与界面剪力分布不均匀有关。

3)单个键群的承载力折减随键群数量增加而增大，四键群试件中单个键群承载力较单键群承载力折减达到28%。

4)基于能量法得出的承载力折减系数与计算的承载力折减系数吻合；提出了预制-装配式中单钉平均抗剪承载力折减系数公式。