重组竹螺栓连接节点承载能力计算分析

李霞镇，任海青，李贤军，徐康，钟永，郝晓峰

(1.中南林业科技大学 材料科学与工程学院，长沙 410004；2.中国林业科学研究院 木材工业研究所，北京 100091)

节点性能是建筑结构载荷传递及整体安全性能的关键，更是结构设计的核心[1-2]。螺栓连接节点因具有制作简单、安全可靠和施工方便等优点，在建筑结构领域广为应用[3-4]，也是现代木结构的首选连接方式。目前，学者们对木材螺栓连接的研究已较为广泛，早在1932年，Trayer[5]就基于轴向压缩加载试验提出了螺栓连接设计公式；1949年，Johanson[6]提出了以预测连接强度为基础的屈服理论模型，用于计算各种形式排布的螺栓连接节点承载强度；而后，Doyle等[7]、McLain等[8]及Soltis等[9]诸多学者均证实了上述结论的有效性和适用性，并对螺栓直径、主侧构件厚度、加载方式、含水率、螺栓排布方式等因素对螺栓连接承载性能影响进行了研究，为后续木结构螺栓连接奠定了理论基础。相比而言，中国在木材螺栓连接领域的研究起步较晚，以哈尔滨工业大学[10-11]、南京工业大学[12-13]及同济大学[14]等为代表的科研院所在木结构螺栓连接方面开展了系列研究工作，为中国现代木结构结构设计提供了一定的理论指导。

随着中国天然林的全面禁伐，大径级木材资源日渐紧缺，而以重组竹为典型代表的新型竹质工程材日益受到人们青睐，并已成功应用于建筑结构中，成为新型工业化建筑的重要材料[15-16]。由于现代竹结构的研究应用时间较短，其连接设计尚未形成统一的理论与技术体系，研究成果相对匮乏，现有设计均参照木结构相关规范进行，且中国2003版GB 50005对重组竹螺栓连接节点承载性能预测的保守性已被多次证实[17-18]。2017版GB 50005已于2018年8月1日正式发布实施，它对螺栓连接承载能力的计算方式做了修订，能够更准确地体现木结构螺栓连接节点的承载能力[11]。为此，以重组竹为研究对象，在开展重组竹-钢夹板单螺栓连接节点特性研究的基础上，分析最新版GB 50005和Eurocode 5规范用于节点承载力计算的准确性，验证最新版GB 50005规范对重组竹螺栓连接承载能力预测的适用性，以期为重组竹结构的连接设计和应用提供科学依据。

1 材料与方法

1.1 试验材料与性能

研究涉及重组竹、钢夹板及螺栓3种试验材料。选用以毛竹为原料生产的重组材，购于安徽宏宇竹木制品有限公司，产品规格为2 000 mm(L)×145 mm(W)×145 mm(T)。根据GB/T 1931—2009、GB/T 1933—2009及GB/T 1935—2009要求，测得其含水率、密度及顺纹抗压强度分别为6%、1.1 g/cm3和73.5 MPa。螺栓所用材料为Q235级钢，强度4.8级。钢夹板所用材料为Q420级钢，厚度6 mm，钢夹板端距为2d(d为螺栓直径)，所导孔径均比相应螺栓直径大1.5 mm。

因重组竹销槽承压强度和螺栓抗弯强度均与螺栓直径有关[19]，根据ASTM D5764-97a和ASTM F1575标准相关要求，分别对重组竹半孔销槽承压强度和螺栓抗弯强度进行测试(图1)，试验结果见表1。

图1 重组竹半孔销槽承压和螺栓抗弯强度试验[18]Fig.1 The half-hole dowel-bearing test of bamboo scrimber and bending yield test of

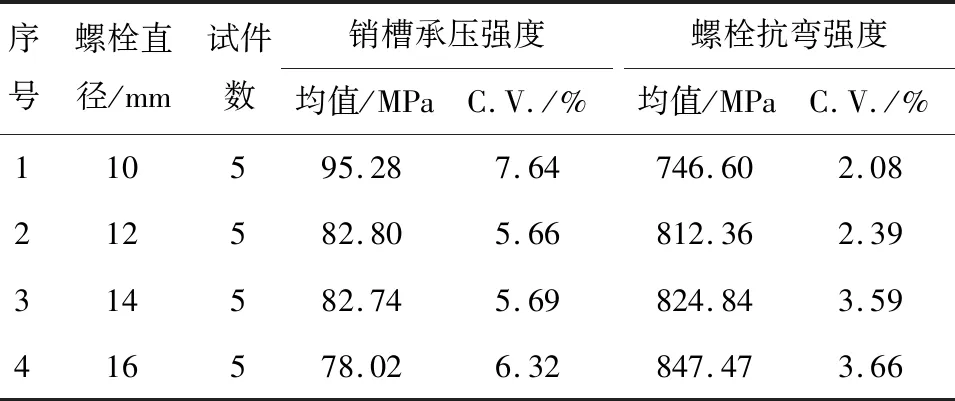
表1 重组竹半孔销槽承压强度和螺栓抗弯强度测试结果Table 1 Test results for the half-hole dowel-bearing strength of bamboo scrimber and bending yield strength of bolts

1.2 试验方案及测试方法

选取螺栓直径、主构件厚度及端距为试验因素进行正交试验设计(表2)，共16个试验组，每组试验重复数为3，共计48个试样。试样加载前，在节点试样两侧分别安装位移计(型号为DDP-20A)后，按ASTM D5652要求进行单轴压缩试验，并将两侧安装的位移计实测均值作为各个螺栓节点试样的实测位移。试验采用30 T微机控制万能力学试验机(型号为WDW-300E)，以1 mm/min的速度实施单轴匀速加载(图2)，直至节点试样破坏或承载力下降至80%的最大载荷，便可停止加载。每个试样加载历程约持续15 min，加载过程中采用静态应变采集仪(型号为TDS-530)实时采集载荷和位移数据，并采用美国木结构设计规范NDS-2005规定的5%螺栓直径偏移法获取节点的屈服载荷，节点承载载荷峰值点所对应的载荷即为极限载荷，具体取值方法详见图3。最后，采用Origin软件，根据曲线的几何特征作图，获取每一节点试样的Foshci理论模型参数P、Δ、M0、M1及k(图4)后，再基于Foshci理论模型各参数之间的数学关系(式1)，利用Origin软件绘制出每一节点试样的Foshci曲线图。

P=(M0+M1Δ)(1-e-kΔ/M0)

(1)

式中：P为载荷，kN；Δ为位移，mm；M0为屈服后渐近线在Y轴上的截距，kN；M1为屈服后刚度，kN/m；k为线弹性刚度，kN/m。

表2 试验设计表Table 2 Experimental parameters

续表2

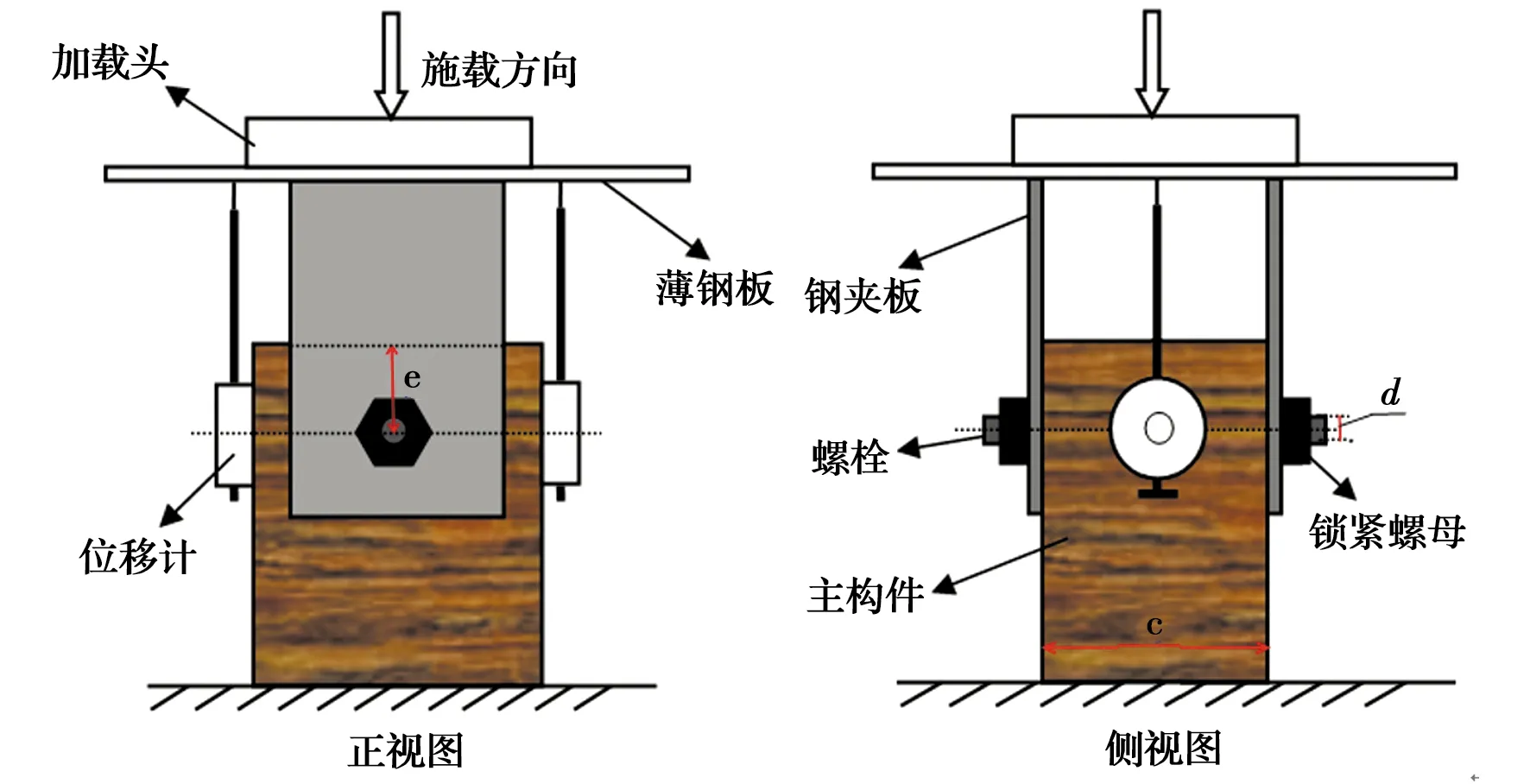
图2 螺栓节点加载示意图Fig.2 Loading diagram of bolted

图3 屈服和极限载荷取值法Fig.3 Method of obtaining Fy and

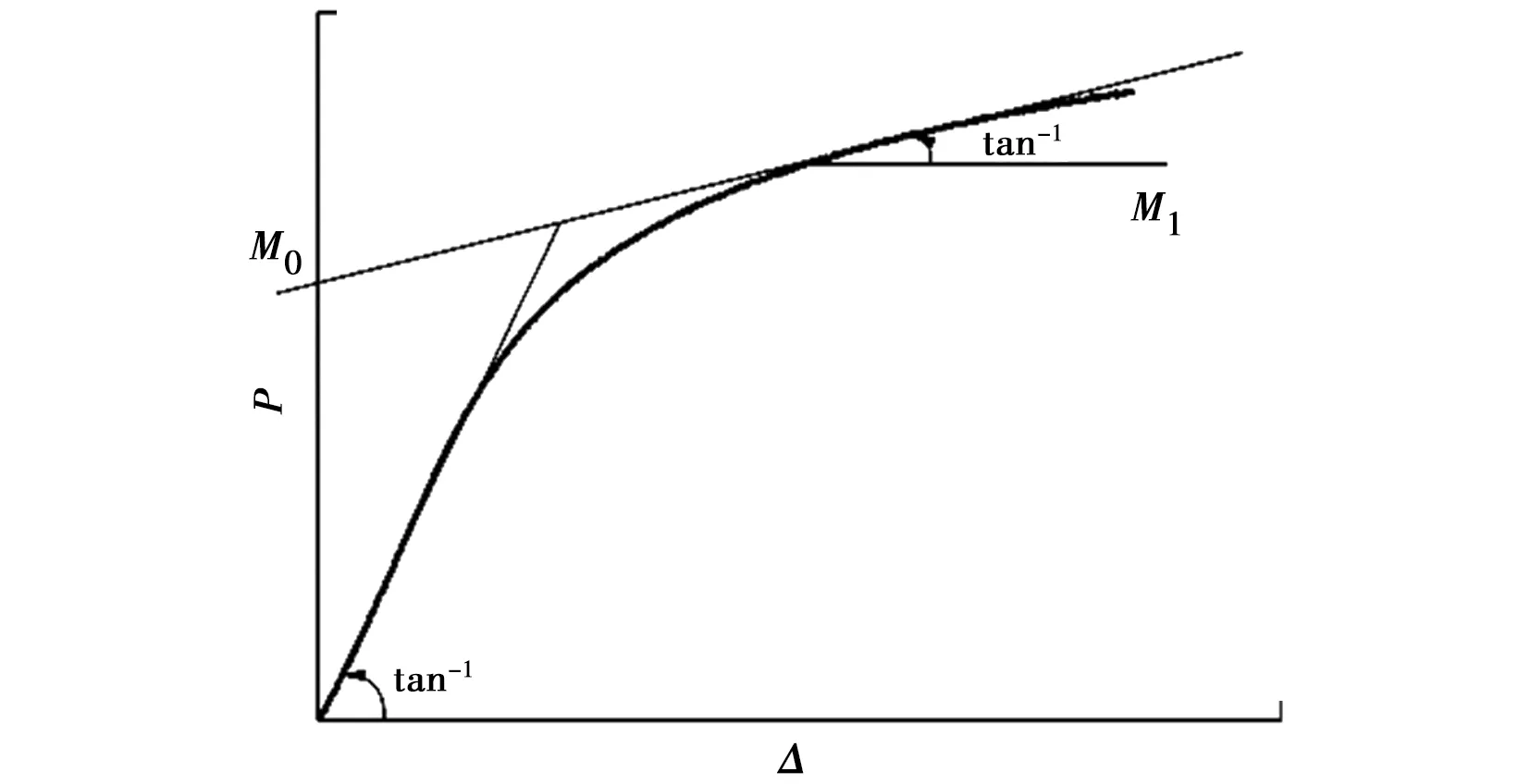
图4 Foshci模型参数的几何特征Fig.4 Geometric characteristics of Foschi model

2 结果及分析

2.1 节点载荷-位移曲线

各组节点试样的载荷-位移曲线均经历了线弹性、弹塑性及破坏3个阶段(见图5)。由于构件与螺栓间存在初始间隙，故载荷-位移曲线在加载初期均有一小段非线性阶段。当载荷增加至一定程度后，初始间隙消失，载荷-位移曲线立即进入线弹性阶段，此时节点各构件均处于弹性变形阶段。随着载荷继续增加，位移迅速增加，此时节点进入弹塑性阶段，曲线处于非线性增长阶段。随着变形继续增加，节点达到极限载荷并发生破坏，曲线瞬间下降，此时节点直接丧失承载能力。

Foschi理论模型基于弹塑性理论而来，它是描述钉、螺栓、齿板等连接载荷-位移曲线的经典公式(式1)，但其参数均需试验测定且随节点参数设置、载荷条件等变化较为敏感，尤其是M0和M1[20]。通过对16组节点试样的载荷-位移曲线和Foshci理论曲线比较发现(图5)，两者的变化趋势基本一致，且在某些部位能够完全吻合。由于节点试样组装时主侧两构件之间存在细微间隙，导致载荷-位移曲线在加载初期有一小段呈非线性状，随着载荷增加至一定程度后才逐渐进入线弹性阶段，故曲线初始阶段的吻合程度稍有差异。但总体而言，Foschi理论曲线能反映节点线弹性阶段和屈服后阶段的变化特征，能较为全面地反映节点整个受力过程，这也说明Foschi理论模型的非线性修正指数函数用以描述重组竹-钢夹板螺栓连接节点的承载性能具有适用性。

2.2 节点承载能力

屈服载荷是节点处于弹性比例极限时所对应的载荷，是衡量建筑结构稳定性的切入点。而极限载荷是指节点在外载荷作用下，在整体或某一局部的全厚度上由弹性状态进入塑性状态时所对应的载荷，此时意味着连接节点即将进入失稳状态。表3和图6给出了节点屈服载荷和极限载荷受螺栓直径、主构件厚度及端距影响的变化情况。屈服载荷和极限载荷随螺栓直径增大呈线性增加趋势(图6(a))，螺栓直径从10 mm增至16 mm时，屈服强度和极限强度分别增加了50.18、48.59 kN。随着主构件厚度增加，屈服载荷基本保持稳定，其值稳定在60 kN左右；而极限载荷呈先增加后稳定的变化趋势，当主构件厚度从60 mm增至90 mm时，其增幅为21.7 kN，当主构件厚度增至90 mm后趋于稳定(图6(b))。随着端距增大，屈服载荷基本保持稳定，其值稳定在60 kN左右；而极限载荷略有下降(图6(c))，推测是由于本研究所设置端距为10d的试样组中，在发生失效破坏前，Φ16-10d-60试样组钢板发生了弯曲，导致其承载能力尚未充分展现所致。

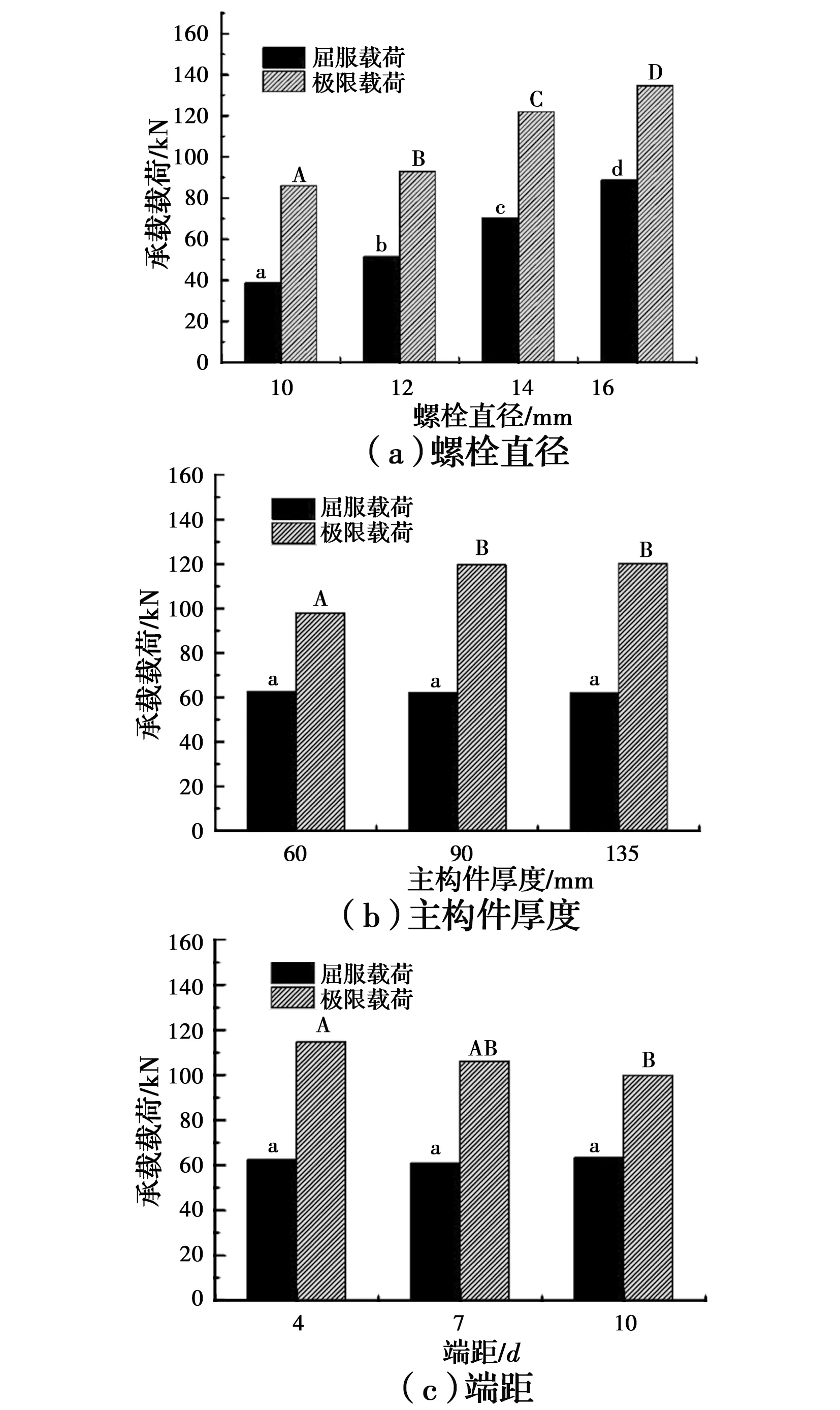
图6 节点承载能力多重比较图Fig.6 Multiple comparison diagram of node bearing

通过方差分析和多重比较(α=0.05)发现，螺栓直径对屈服载荷和极限载荷影响均显著(P值均为0.000)，且两两试样组间均存在显著差异(同一图中的不同字母表示两者之间存在显著差异；反之，两者间无显著差异)；主构件厚度和端距对屈服载荷影响不显著(P值分别为0.324、0.811)，但对极限载荷影响均显著(P值分别为0.006、0.000)，说明极限载荷受螺栓直径、主构件厚度及端距三因素共同影响，与前人得到的单螺栓极限载荷受端距和厚径比影响的结论一致[21]，同时也反应出当螺栓连接节点达到最小尺寸设计要求时，其承载能力受螺栓直径影响作用最为明显。

16组节点试样均以Ⅲm型和Ⅳ型屈服破坏模式呈现，其中，螺栓直径为10、12 mm，节点多为Ⅳ型，而螺栓直径为14、16 mm的节点以Ⅲm型呈现(图7)。由于主要侧重对节点承载力的预测分析，在此对节点的破坏模式、刚度、延性率等其他性能不过多地做比较分析。

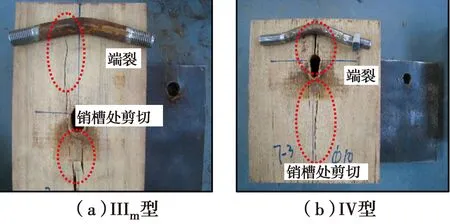
图7 节点试样典型破坏模式Fig.7 Typical failure modes for the

2.3 节点承载能力计算分析

因连接节点的结构承载设计值应考虑整体结构安全稳定性，故各国规范均将安全系数纳入结构设计的考虑范畴。但由于荷载和抗力的统计参数不同，包括节点破坏标志点和抗力计算方法不同，导致安全可靠度计算方法亦不同，因此，不同国家规范间的可靠度安全系数并不等价。为了更准确地评价连接节点本身的承载能力，在使用各国规范进行承载力计算时，未将安全系数纳入考虑范畴，直接基于连接节点承载力试验值进行比较分析。

中国2017版GB 50005在2003版的基础上对螺栓节点承载力计算公式做了修正，用木材销槽承压强度替换了木材顺纹抗压强度，且突破了2003版对螺栓节点中对被连接木构件的木材材质等级相同的假定，能够适用于不同材质、不同强度等级的构件组合而成的连接节点。2017版GB 50005虽未直接规定钢夹板连接节点承载力的计算方法，但采用了美国NDS-2005规范的方法，在钢夹板销槽承压强度不起控制作用时，可直接将钢板视为一种销槽承压强度很高的“木材”，故钢夹板承载力的计算方法与普通木材螺栓连接节点相同，只需将边构件的销槽承压强度采用相应钢板的销槽承压强度便可，且在螺栓承载力计算中，对于钢销产生塑性铰的屈服模式是基于塑性不完全发展理论的[22]。不论基于何种屈服模式，螺栓连接承载力的计算均可归结为销槽有效承压长度或销槽有效承压长度系数的确定。由于一般情况下钢板不发生销槽承压破坏，故利用主构件计算节点的承载力。鉴于此，可将2017版GB 50005所规定的螺栓连接节点每一剪切面承载力的理论计算公式表示如式(2)～式(4)，并取3种模式下的最小值作为节点承载力理论计算值。

(2)

(3)

(4)

式中：α=c/a，c和a分别为主构件厚度和边构件厚度；β=fhc/fha，fha和fhc分别为边构件和主构件的销槽承压强度；d为螺栓直径；η=a/d，为销径比；kep取1.0；fyk为螺栓抗弯屈服强度。

欧洲木结构设计规范Eurocode 5中的螺栓连接节点破坏模式和相应承载力计算公式是基于Johanson屈服理论提出的，单独给出了钢夹板和钢填板螺栓连接节点每一剪切面承载力的计算式(式(5))，并将钢板分为薄钢板、厚钢板两种情况，且认为厚钢板对螺栓转动有足够的钳制力，一般取j和m模式下的较小值作为理论计算值；而薄单板无明显约束力，其单一剪面承载力的理论计算值则取j和k模式下的较小值。其中，式(5)中的破坏模式j、k及m分别对应中国Ⅰ型、Ⅲ型和Ⅳ型破坏模式。

(5)

式中：Fv,Rk为每个剪切面的承载力；t2为主构件厚度；fh,2,k为主构件销槽承压强度；My,Rk为螺栓屈服弯矩，My,Rk=(fbsd3)/6。

试验中螺栓连接节点均呈现Ⅲm型和Ⅳ型破坏模式，根据钢板厚薄程度，分别采用模式k和m的公式计算各组螺栓连接节点的承载力。其中，钢板薄厚以钢板厚度t和螺栓直径d的比值区分，当t/d≥1时，视为厚钢板；当t/d≤0.5时，视为薄钢板；当0.5

以Φ10-10d-60试样组为例，分别依据2017版GB 50005和Eurocode 5规范计算该螺栓节点的承载力理论计算值。其中，该试样组的螺栓直径为10 mm、主构件厚度为60 mm、主构件销槽承压强度为95.28 MPa、螺栓抗弯屈服强度为746.6 MPa、侧构件销槽承压强度为484 MPa(钢板为Q420钢，根据GB 50017所给出的钢材销槽承压设计值440 MPa的基础上，将其材料分项系数估计为1.1，此处取1.1倍的设计值作为其强度标准值[11])、kep取1.0。此时，利用式(2)～式(4)求得3种屈服模式下螺栓节点试样单一剪面的承载力理论计算值分别为56.27、26.62、35.56 kN，取三者中的最小值作为理论计算值，即为26.62 kN。因该节点为对称双剪连接，故该节点的承载力理论计算值即为53.24 kN。

由于Φ10-10d-60螺栓节点的钢板厚度为6 mm、螺栓直径为10 mm，其t/d值处于0.5和1之间，利用Eurocode 5规范计算承载力时，应按薄、厚钢板两种情况的线性插值法求解节点单一剪面的承载力。基于式(5)计算所得屈服模式j、k及m所对应的单一剪面承载力分别为28.58、17.71、25.04 kN，取k和m模式下所对应的计算值17.71、25.04 kN进行线性插值求解，得该节点单一剪面的承载力计算值为19.18 kN，故该螺栓节点承载力的理论计算值为38.36 kN。

根据2017版GB 50005和Eurocode 5规范规定的承载力计算公式，获得16组连接节点承载力计算值(见表3)。整体而言，基于两规范计算的承载力理论计算值普遍比试验值偏小，其中2017版GB 50005的理论计算值与实测值较为接近，但Eurocode 5的计算值误差相对较大，这主要是由于Eurocode 5的承载力计算考虑了“绳索效应”，即节点需要在很大的弯曲变形情况下，才可能在螺杆中产生显著拉力并产生侧向力方向的分量，但本试验所用的钢夹板螺栓连接因其形变量小，“绳索效应”可忽略不计，致使各节点承载力理论计算值明显小于试验值，这也进一步验证了欧洲规范在不计“绳索效应”情况下承载力计算结果偏低的结论[11]。对于2017版GB 50005理论计算值略有偏低但与实际情况较为接近的原因，主要是由于该规范对螺栓承载屈服的计算基于塑性不完全发展的塑性铰的计算方法，使得螺栓节点承载力计算与实际工况较为接近。但从另一方面而言，2017版GB 50005承载力计算基于理想弹塑性材料本构模型，导致其中部分屈服模式下的节点承载力理论计算值存在略有偏低的情况[23]。

从表3中还可以看出，Φ10-7d-135、Φ12-10d-135、Φ14-4d-135及Φ16-4d-135四组试样基于2017版GB 50005计算的承载力明显偏大，这主要是由于4组螺栓连接节点所设置的主构件厚度均为135 mm，其对应的厚径比(c/d值)相对较大，分别为13.50、11.25、9.64及8.44，对整个连接节点而言，其具有“少筋”特征，螺栓在主构件破坏前发生明显屈服破坏现象，而主构件本身却未发生明显破坏，此时主构件的力学承载性能尚未充分展现，导致螺栓连接节点承载力试验值明显偏低；再者，因中国2017版GB 50005对螺栓承载能力的预测基于螺栓和主构件同时发生屈服破坏的基础上，故导致以上4组试样的理论计算值与实测值存在较大偏差。这也说明，使用设计规范预测节点承载力的前提是节点的几何构造特征应满足相应设计要求，尽量保证连接件和主构件的力学优势能够最大限度地发挥，使材料物尽其用。由表3可知，Φ10-10d-60、Φ10-4d-60、Φ12-7d-60及Φ12-4d-60四组节点实测值和理论计算值的偏差较其余试样组稍大，这主要是由于以上4组节点试样均呈Ⅳ型屈服模式，在钢板处形成了两个塑性铰，且因各节点的销槽压力力臂小于在木构件内部形成塑性铰的情况，致使以上节点所形成塑性铰所需施加的作用力增大[23]；再者，以上4组节点试样的螺栓和主构件同时发生了屈服破坏，此时螺栓和主构件的承载能力均能充分发挥，最终表现出节点承载能力实测值比理论计算值偏大。这类屈服模式也正好与以上所提及的“中国2017版GB 50005对螺栓承载能力的预测基础(即螺栓和主构件同时发生屈服)”相吻合，属于最为理想的屈服破坏模式，也进一步印证了中国2017版GB 50005中部分屈服模式下的节点承载力计算值会略有偏低的情况。整体而言，采用2017版GB 50005计算所得的重组竹螺栓连接承载力误差相对Eurocode 5较小，计算值与试验值之间存在一定安全富余的空间，可以较好地预测重组竹-钢夹板螺栓连接的承载力。

表3 节点承载力试验值与理论计算值对比Table 3 Comparison between experimental and theoretical values of joint bearing capacity

续表3

3 结论

通过对16组48个重组竹-钢夹板单螺栓连接节点试样进行试验分析，揭示了螺栓直径、端距及主构件厚度等因素对节点承载能力的影响规律，验证了Foshci理论模型对重组竹-钢夹板单螺栓连接节点的适用性，分析评价了2017版GB 50005和European 5规范对重组竹-钢夹板螺栓连接承载力预测的准确性，主要结论如下：

1)Foschi理论模型能够反映节点试样的线弹性阶段和屈服后节点的变化特征，能较为全面地反映节点试样的整个受力过程，这也进一步证实了Foschi理论模型用于描述重组竹-钢夹板单螺栓连接节点的承载性能的适用性。

2)螺栓直径对屈服载荷和极限载荷影响显著，且屈服载荷和极限载荷随螺栓直径增大呈线性递增趋势；端距和主构件厚度对屈服载荷影响不显著，但对极限载荷影响显著。这反映出当螺栓连接节点达到最小尺寸设计要求时，其承载能力受螺栓直径影响作用最为明显。

3)Eurocode 5对重组竹-钢夹板单螺栓连接节点的承载力预测偏保守；而中国2017版GB 50005对重组竹螺栓连接节点承载力预测存在安全富余空间，在节点的几何构造特征满足最小尺寸要求的前提下，能够较好地预测重组竹-钢夹板螺栓连接节点的承载力。