双重信息非对称下的敏捷供应链契约设计
冉文学,郑文文 (云南财经大学 物流学院,云南 昆明 650221)
0 引 言
敏捷供应链是在20世纪90年代末被提出来的,随着计算机与互联网技术的不断成熟,敏捷供应链也被越来越多的学者们所关注并且研究。敏捷供应链是在外界环境不断变化的情况下,而形成的一个富有竞争力和创造力的同盟,运用多种科技手段,以供应链主体为中心,掌控供应链的物流、资金流、信息流,将供应商、分销商、零售商及终端客户整合在一起的战略联盟,以期能在终端客户需求变化时能够迅速的做出反应,更好地服务于终端客户。进入新世纪以来,随着全球经济不断的提高,我国经济也在高速的发展,各项技术都在发展创新,市场环境也在不断的变化,客户的需求变化也更加的不确定。敏捷供应链中,主体企业与其相关企业之间是契约形式的合同关系,尽管相信各个企业之间能够共享所有所知道的信息,但是每个企业都追求的是成本最小化与利益最大原则,因此可能存在某些企业会隐藏自己所知道的一些重要信息,造成信息不对称的现象。在道德风险与逆向选择存在的情况下,敏捷供应链运作效率降低,使整体利益受损,因此消除信息非对称现象就显得至关重要,那么敏捷供应链主体企业如何提高相关企业的努力程度并识别其是否隐匿信息,则是关键因素。
学者们针对敏捷供应链问题做了广泛的研究,并取得了一定成果。蒲国利等(2019)基于动态能力的视角,考虑了供应链弹性的相关问题,从三个方面、三个阶段对供应链弹性进行分析,并探讨了供应链弹性未来的研究方向。王道平等(2017)从知识服务网络的角度来分析敏捷供应链,使知识能够在敏捷供应链相关企业之间进行传递。廖凯诚等(2020)考虑了集体横向竞合与供应链敏捷性之间的关系,认为两者之间存在三条路径,并研究三条中介路径对供应链敏捷性的影响大小。孙新波等(2019)从大数据驱动的视角出发,研究大数据与企业供应链敏捷性之间的关系,认为合理运用大数据可以提高企业供应链敏捷性。胡亚男(2020)从合作伙伴选择方法上考虑敏捷供应链,并提出了最符合现在市场的敏捷供应链合作伙伴选择方法,即多属性群体决策方法。Xiang Ning Zhu等(2021)认为静态下的供应链满足不了当下企业追求低消费高收入的发展,因此对敏捷供应链提出了新的框架结构,该框架将物联网和区块链技术融合其中。Ayman Bahiat Abdallah与Haya Fawzi Ayoub(2020)根据约旦的多个制造公司的调查数据,探索影响供应链敏捷性的信息技术驱动因素,并研究这些因素对敏捷供应链实施水平的影响以及供应链敏感性对市场绩效的影响。David Cahn(2020)根据新冠疫情对社会以及各大企业的影响,表达在环境发生变化时,企业需要及时做出反应的观点,进一步突出了敏捷供应链的重要性。Akram Chibani等(2018)根据电子采购短时间内高度变化的特点,考虑供应链应具有高度的敏捷性,以优化采购过程。学者们对敏捷供应链的各项特点、结构、模型及敏捷供应链的其他方面都进行了深度的研究,但是很少有学者对道德风险和逆向选择情况下敏捷供应链主体企业应该如何应对。然而已经有一部分学者进行了信息非对称下供应链的相关研究。王静(2014)从农产品领域出发,研究虚拟供应链物流信息系统模式,分析了该模型下道德风险与逆向选择所带来的问题,在此基础上提出了防范对策。冯常源(2018)从虚拟供应链风险的特点出发,比较虚拟供应链与传统供应链风险的异同点,并且构建出虚拟供应链风险评估的模型,基于该模型提出了针对性的建议。
本文将借鉴上述研究成果及思想,考虑信息非对称时敏捷供应链主体企业如何应对。本文将从项目工期、成本、努力程度等其他因素的角度分析,建立激励模型,根据该模型,对敏捷供应链相关企业的私有信息与努力程度进行分析,从而更好地避免道德风险与逆向选择双重问题对敏捷供应链的损害。本文主要分两个方面来进行分析,首先分析单一信息非对称下的最优激励契约模型,基于单一条件模型,进而分析双重信息非对称下的最优激励模型,从而研究双重信息非对称对敏捷供应链主体企业与相关企业决策和收益的影响。最后本文运用具体算例分析来验证本文方法的可靠性和实用性。
1 问题描述及模型假设
在敏捷供应链中,根据敏捷供应链主体要求其相关企业完成的项目,引入模型T=t-ka-θ+γ,从而更好地分析相关企业完成项目的所需时间及努力程度。其中T表示实际完工的时间,t表示最大可能完工的时间,a是相关企业的努力程度,k代表相关企业努力程度的系数(k> 0),θ代表相关企业的私有信息,γ代表其他的影响因素。其中θ由于是相关企业的私有信息,因此敏捷供应链的主体企业无法准确获取其相关值,但是可以发现其概率密度、分布函数及数学期望,分别为f(θ)、F(θ)及μ。
已知完成项目所需要的工期越长,其成本就越高,项目工期与成本之间呈正比关系。因此项目的利润为π(T )=r-rT,其中r表示项目的收益,r表示单位时间的成本,rT表示完成该项工期所需要的成本。由于相关企业的努力程度不易被敏捷供应链主体企业观测到,主体企业易获得相关企业完成项目的时间,因此设相关企业的努力成本为C(a)=ba/2。为了使相关企业尽早完成项目工作,需要对其进行激励,引入线性激励模型为s(T)=α-βT,其中α为固定的支付,β为激励系数(β≥ 0)。
下面分别从敏捷供应链主体企业以及敏捷供应链相关企业双方的决策问题进行分析。敏捷供应链主体企业的决策问题是确定其相关企业的固定支付α及激励系数β,进而使其效用最大化。假设敏捷供应链主体企业是风险中性的,期望效用为其期望收益,则其期望收益模型:

相关企业的净收益为:

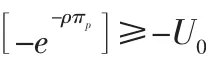
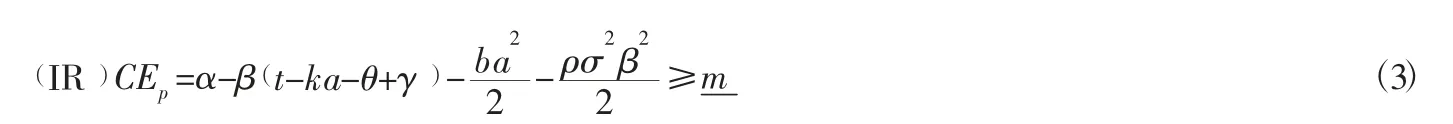
敏捷供应链主体企业在做决策之前就应该预测到,只有满足式(3)的个人理性约束(IR)条件时,相关企业才会接受敏捷供应链主体企业的契约,并且会选择能够满足其期望效用最大的努力程度。在该条件下,敏捷供应链主体企业为了实现利益最大化,需要制定出相应的报酬函数s(T)。
本文为了更方便研究信息非对称下的敏捷供应链主体企业的最优契约、敏捷供应链主体企业及其相关企业将受到哪些影响,在单一信息非对称时,将道德风险作为研究条件,在双重信息非对称时,将道德风险与逆向选择共同作为其研究条件,以期能够获得符合现实的结论,对当下的敏捷供应链有指导意义。
2 单一信息非对称的情形
由于敏捷供应链的主体企业不能观测到其相关企业的努力程度,因此相关企业可能做出对主体企业不利的行为。因此敏捷供应链主体企业要设计出相应的契约,以期更好地对相关企业进行激励,使其提高努力程度。最优激励模型可以通过以下模型得到:


上述模型中的IC是敏捷供应链相关企业的激励相容约束。由于每个人都尽量追求个人利益最大化,因此需要安排一种管理制度,使个人利益服从与集体利益,个人利益适应于集体利益,个人利益最大化的实现是以集体利益最大化的实现为前提,这就是激励相容。在敏捷供应链中,由于信息非对称,敏捷供应链相关企业会选择对自己最有利的努力程度。因此敏捷供应链主体企业需要根据上述两个约束条件来设计契约。
根据公式(3)可以得知CE是a的凹函数,对a求一阶导得a=kβ/b,将a分别代入到敏捷供应链主体企业的目标函数和其相关企业的个人理性约束条件中,得到如下优化问题:
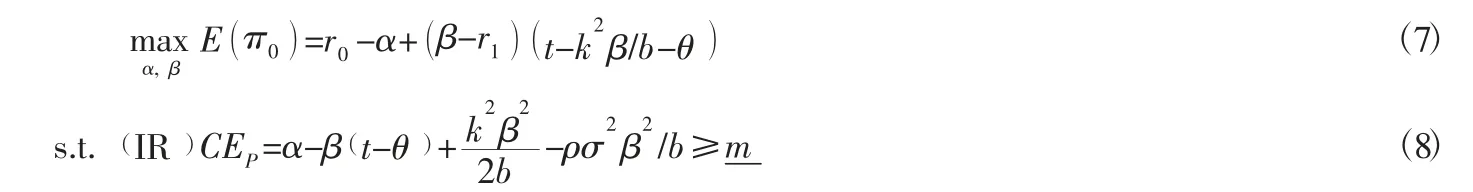
构造Lagrange函数:
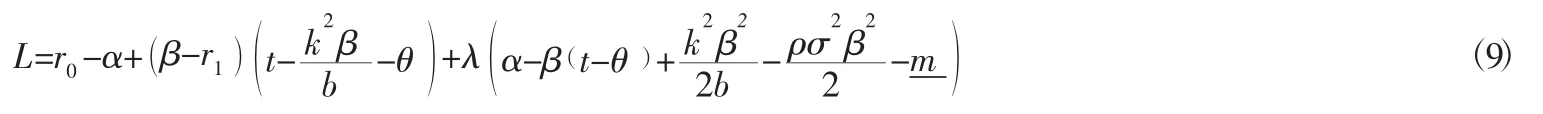
分别对Lagrange函数中的α,β,λ求偏导,并令其偏导结果等于0,可首先解得λ=1。再将λ=1分别代入其余偏导公式中,可分别解得β与α,即:
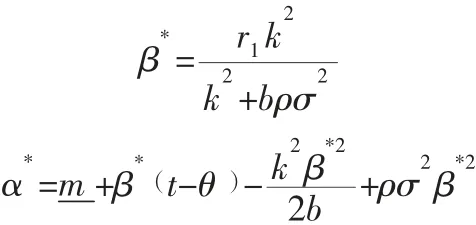
将求解的α与β代入敏捷供应链主体的目标函数中,可以得到E(π),即:
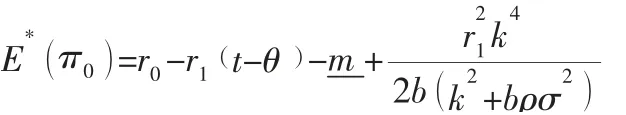
由此可以得出以下定理:
单一信息非对称条件下,即道德风险非对称条件下,最优契约应该满足以下配置:

敏捷供应链相关企业的最优努力程度及敏捷供应链主体企业的最大期望收益分别为:
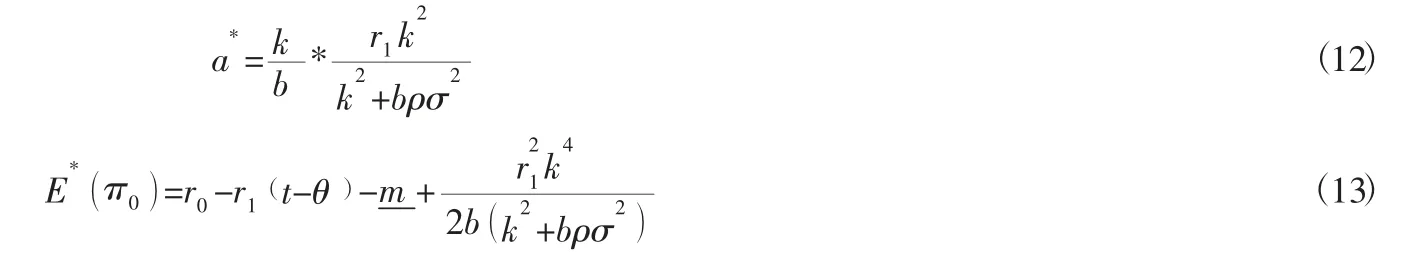
基于此易得出最优的期望完工时间和期望收益。在期望完工时间上根据最开始建立的模型,将a代入到该模型中,即可得到期望完工时间E(T)。期望收益则是根据项目的利润模型得到的结果。因此道德风险非对称条件下,项目的最优期望完成时间和期望收益分别为:
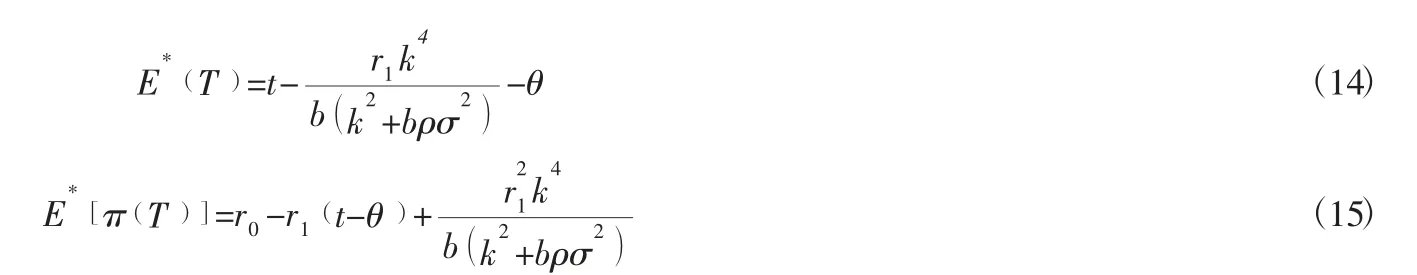
由a、β表达式可知,敏捷供应链相关企业的努力程度随着b、ρ、σ的减小而增大,相关企业的激励程度与努力程度有相同的结论。对固定支付α而言,项目的实施条件θ越小时,固定支付就越高,θ越大时(实施条件越好),固定支付就越小。由a、β的表达式可知,敏捷供应链相关企业的努力程度以及激励强度与θ无关。
3 双重信息非对称的情形
将上述的研究假设条件进一步放宽,研究双重信息非对称条件下的激励问题。敏捷供应链主体企业与其相关企业签订契约时,由于将非对称的条件放宽,因此敏捷供应链主体企业将遇到道德风险与逆向选择的双重信息非对称的问题。在签订契约之前,敏捷供应链主体企业与其相关企业之间存在着逆向选择的问题,即相关企业的私有信息是不能被主体企业所观测到的,存在着私有信息θ的非对称。在双方签订契约之后,双方存在着道德风险的问题,即相关企业的努力程度是不能被主体企业所观测到的,存在着相关企业努力程度信息非对称。在此双重信息非对称的条件下,敏捷供应链主体企业需要进一步判断其相关企业所提供的信息是否真实有效,并且需要激励相关企业提高其努力程度。
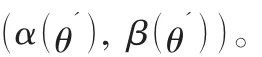
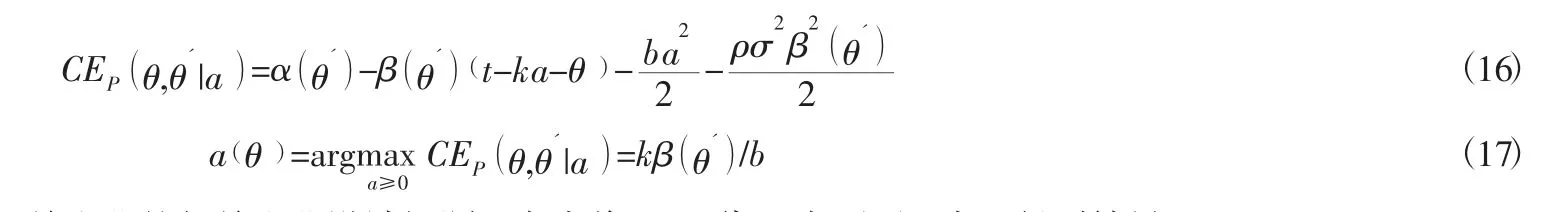
为了更好地解决敏捷供应链相关企业的相关企业设计问题,考虑将a(θ)代入式(16)中,得到结果:
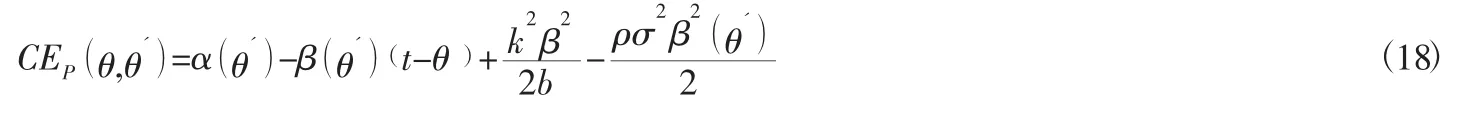
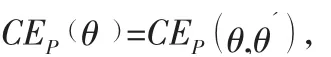


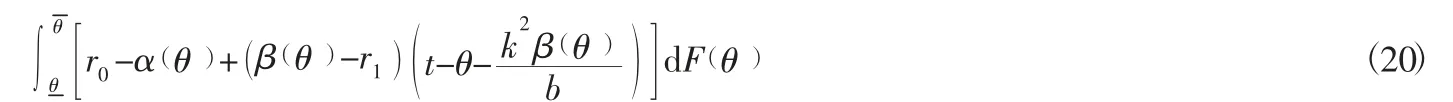
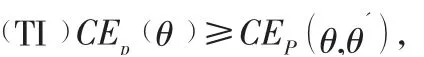
尽管敏捷供应链主体企业并不知道其相关企业具体的私有信息,但是主体企业已经知道其概率分布,因此主体企业在与其相关企业签订契约后,仍会不断地修改契约。所以,需要对以下问题进行优化:
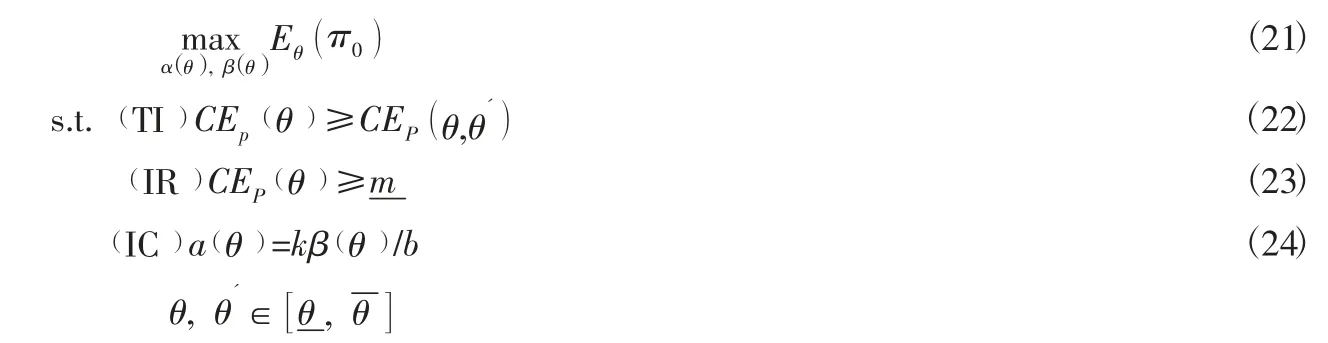
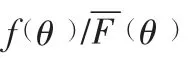

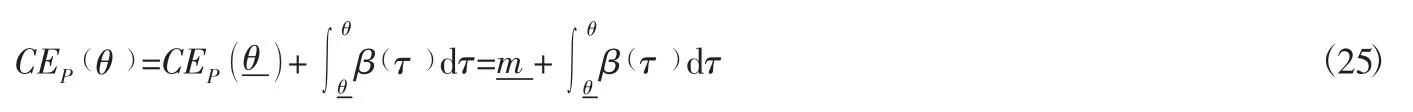
根据式(19)可知:

所以:
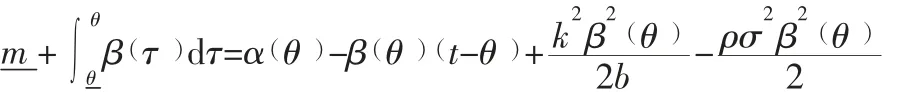
得出:
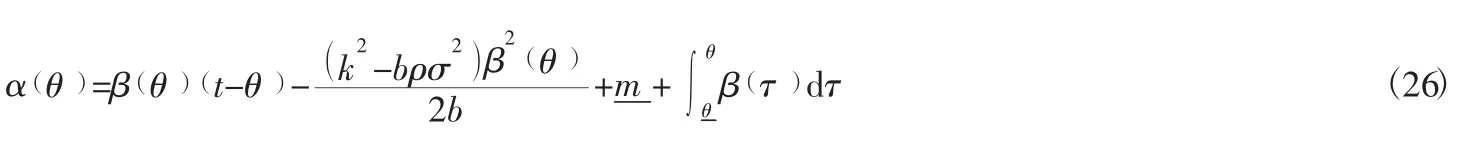
将α(θ)代入到敏捷供应链主体企业中,可得:
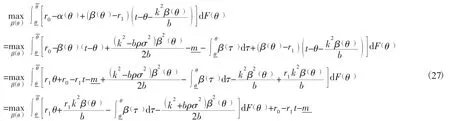
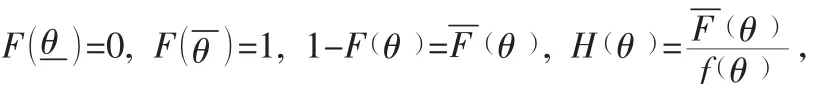
交换积分次序,得:
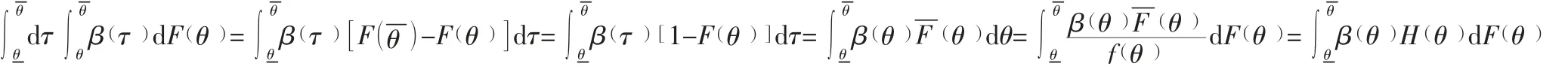
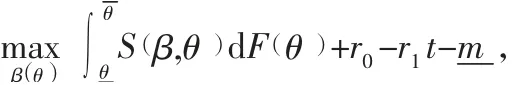
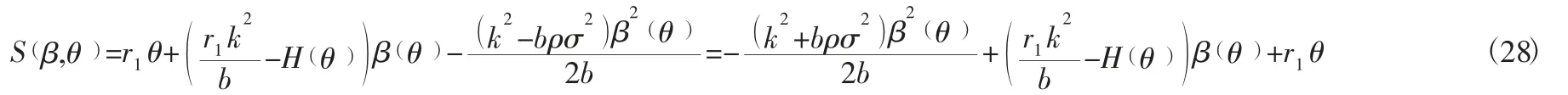
将该式子看成一个关于β(θ)的一元二次方程,因此β(θ)的最优解为:
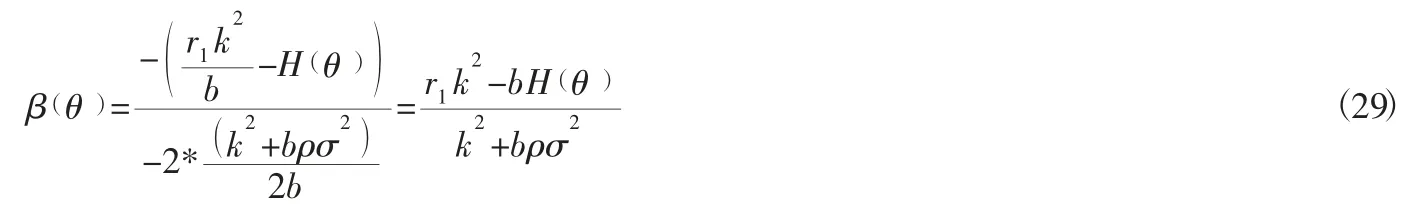
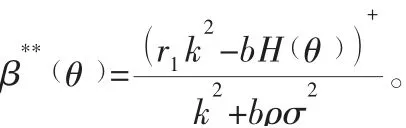
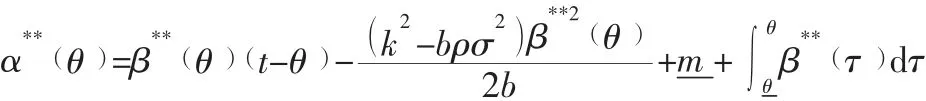
敏捷供应链相关企业的最优努力程度为:
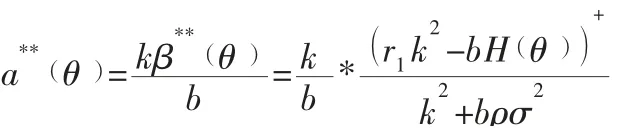

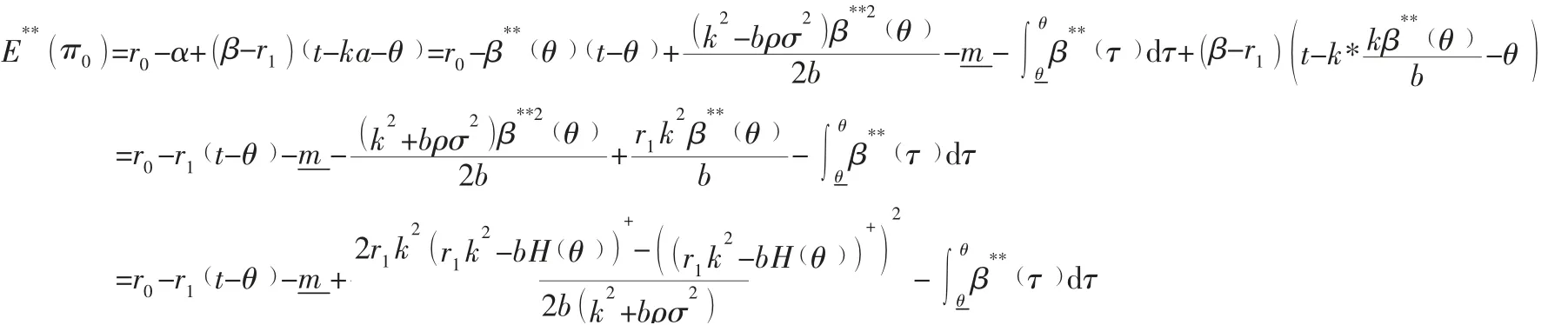
所以,双重信息非对称条件下,敏捷供应链相关企业的真实的私有信息θ及努力程度不被主体企业所了解时,敏捷供应链主体企业给出的最优契约应满足以下条件:
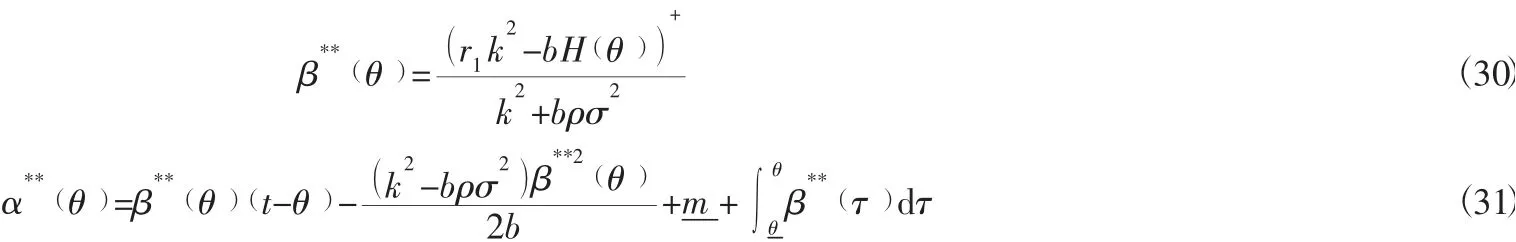
敏捷供应链相关企业的相应最优努力程度为:
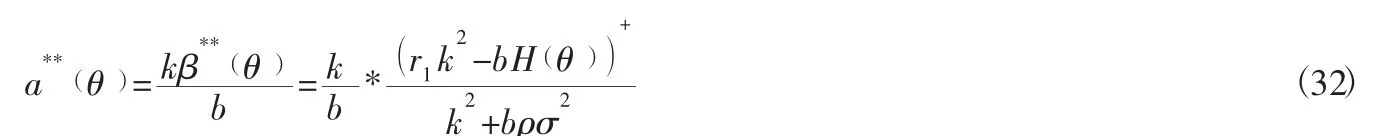
敏捷供应链主体企业的最大期望收益为:
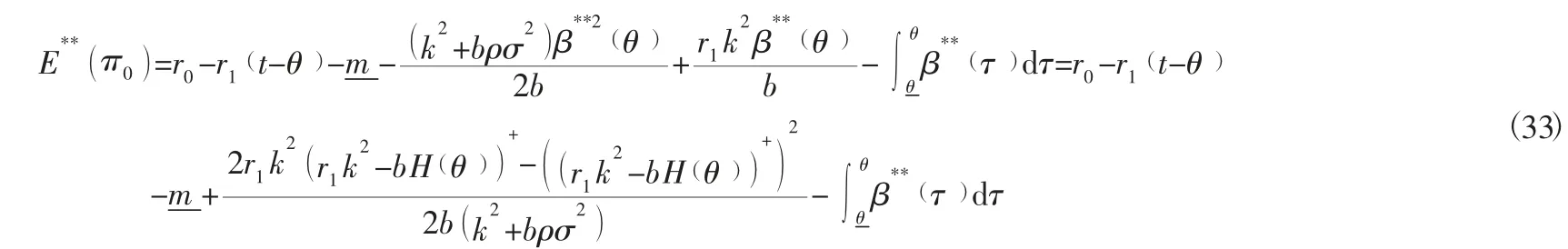
敏捷供应链相关企业的收益为:

由此易得出最优的期望完工时间和期望收益。在期望完工时间上根据最开始建立的模型,将a(θ)代入到该模型中,即可得到期望完工时间E(T)。预期收益是根据项目的盈利模式得出的结果。因此在同时考虑道德风险与逆向选择的情况下,最优的期望完工时间和期望收益分别为:

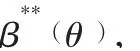
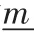

表明敏捷供应链相关企业隐藏的私有信息越多,其获得的额外收益就越多。隐藏的私有信息越少,敏捷供应链主体企业越没有优势。
4 算例分析
以上分析主要是从结论和性质出发,为了更加直观地表达单一信息非对称条件下与双重信息非对称条件下,敏捷供应链主体企业与其相关企业的决策和收益,本文将代入具体的数值,进行进一步的比较和分析,从而验证本文的定理与结论。
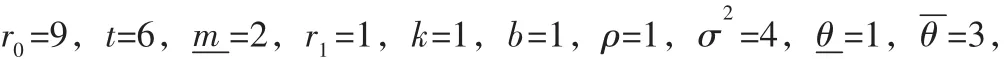

图1显示的是真实信息对敏捷供应链相关企业努力程度的影响及比较。如图1所示,在单一信息非对称(道德风险)条件下,敏捷供应链相关企业的努力程度与真实信息θ是无关的。在双重信息非对称(道德风险与逆向选择并存)条件下,敏捷供应链主体企业对其相关企业的真实信息了解的越少,则相关企业付出的努力程度就越小。此结果与本文的结论2相一致,进一步验证了本文的结论。
图1 θ对敏捷供应链相关企业努力程度的影响及比较
图2显示的是真实信息对敏捷供应链相关企业收益的影响及比较。如图2所示,在道德风险非对称条件下,敏捷供应链相关企业的收益为保留收益,与真实信息θ是无关的。在双重信息非对称条件下,敏捷供应链相关企业除了得到保留收益外,还获得了额外收益。这与本文的结论3相一致,进一步验证了本文的结论。
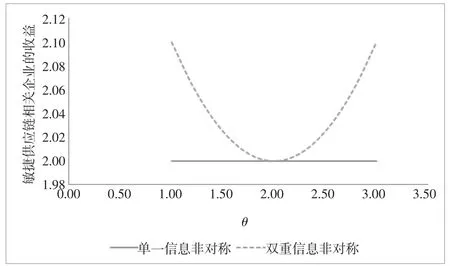
图2 θ对敏捷供应链相关企业收益的影响及比较
图3显示的是真实信息对敏捷供应链主体企业收益的影响及比较。如图3所示,在区间1,[]2之间,单一信息非对称条件下敏捷供应链主体企业的收益高于双重信息非对称条件下的收益。在区间[2,3]之间,单一信息非对称条件下敏捷供应链主体企业的收益略低于双重信息非对称条件下的收益。这与本文的结论1相一致,进一步验证了本文的结论。
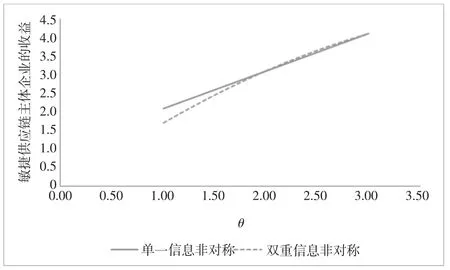
图3 θ对敏捷供应链主体企业收益的影响及比较
5 结束语
本文首先研究单一信息非对称条件下,即道德风险存在的条件下,敏捷供应链主体企业不能观测到其相关企业的努力程度时,如何提高其相关企业的努力程度的契约问题。之后研究在双重信息非对称下,敏捷供应链主体企业不能观测到其相关企业的私有信息及努力程度时,如何提高其相关企业的努力程度,并且识别其相关企业的真实信息的契约设计问题。分别构建了相应的激励模型,并对所得到的模型进行分析。对这两种情况进行比较分析,结果显示在同时考虑道德风险与逆向选择非对称时,与单一的考虑道德风险非对称相比较,两种情况在契约上有着不同的特征。

