考虑分级配送的震后应急物流选址—路径研究
张步阔,魏志铭,陈 刚 (贵州大学 管理学院,贵州 贵阳550025)
0 引言
近年来,地震灾害频发,尤其唐山大地震、汶川大地震等重大地震灾害对受灾区域的人员安全和经济发展都造成了巨大的影响,直接影响了社会秩序。每当地震灾害发生时,尤其在震后初期,受灾区域的公共设施、道路与建筑等都会受到地震冲击的影响,使得受灾区域的人员无法获得充足的应急物资以保证自身安全。在此背景下,救援工作的展开往往会受到多方因素的干扰变得十分复杂,因此为了能够在震后快速地进行应急决策,将应急物资快速、科学地送达到受灾区域,就要合理的利用震后应急物流系统在较短时间内找出能够被决策者所接受的优秀方案。
应急物流系统的研究主要包括了应急物流选址与应急物资配送。对于物流选址研究,早期的学者主要聚焦于单目标规划的研究中,而随着物流选址研究的不断深入,多目标的规划已经慢慢成为路径—选址研究的主流方向。
在当前应急物流系统选址研究中,成本、时间、公平性是主要的考虑因素。赖志柱、马祖军以应急物流的最小救援时间和总救援成本为目标建立了震后应急物流选址模型。张进峰基于库区水域应急救助工作,引入安全系数建立了考虑公平性、时效性、可靠性的多目标优化模型。宋英华综合考虑了道路的损毁情况与不同物资的动态需求建立了以时间、成本与公平性的震后快速选址模型。
虽然在应急物流选址方面已经有较多研究,但当前大多数研究通常只就一两个因素进行深入考虑,同时对于决策者的决策偏好也缺乏思考,难以全面地对路径—选址问题进行研究。因此为了更加契合实际,本文考虑不同决策者的决策偏好差异建立了同时考虑时间满意度、成本满意度与公平性的多目标规划模型。
在应急物资配送研究方面,当前的研究主要是通过启发式算法的编码方式模拟所有可能的方案来确定应急救灾物资配送的全过程,一定程度上降低了算法的效率与稳定性。同时,在应急救援中,许多学者主要对单一运输方式的应急物资配送进行研究。虽然也有研究对多种运输方式进行考虑,但大多只将其应用到从物资集散点到物资中转站的前半部分,并未将多种运输方式应用到中转站到受灾点的配送中。但由于地震灾害的独特性质,在震后初期路面道路往往会受到不同程度的损毁,导致路面道路无法通行。
因此为快速、稳定的得出优秀的应急方案,提高应急工作效率,本文将航空运输加入到物资运输的工作中,形成多种运输工具混合运输的工作模式来对各受灾点进行分级配送,并综合时间、成本、道路损毁程度等多种因素求解出决策者可以接受的最优解集,为应急管理者寻求最优方案提供决策支持。
1 模型建立
1.1 问题描述。在地震发生后,需要快速的启用应急物资配发站,在时间、空间、资源等因素的限制下高效地将有限的救援物资运输到各个受灾点以满足当地人员的需求。尤其在震后初期,公共设施不同程度损坏,受灾区域人民难以获取足量应急物资,此时就需要调动临近的物流中心,将预先存贮的应急物资高效、快速地分配给各受灾点以满足受灾人员需要。
1.2 假 设
(1)受灾点的最低需求物资量和道路损毁情况都是已知的。(2)高优先级救援物资(如食物、饮用水、药品、衣物等)成套打包运输至受灾区域。(3)将运输直升机加入应急的队伍构成中,与公路运输共同参与路径的优化。(4)每个应急物流中心的存贮物资是有限的,将已开启应急物流中心的救援物资全部用于救援。
1.3 符号说明
1.3.1 参数。R表示受灾区域内受灾点集合,R表示集合内顺序为i的受灾点,i=1,2,3,…,N;J表示应急物资配发站集合;E表示救援飞机集散点;K表示从应急物流中心到受灾点过程中采用受道路情况影响的公路运输工具集合;K表示从应急物流中心到受灾点过程中采用不受道路情况影响的航空运输工具集合;从应急物流配发站到受灾点过程中运输方式的集合,K=K∪K;N表示受灾点个数;Cap表示运输工具k的载重量;C表示救援工作总成本;CW表示物流中心j的开启费用;V表示救援直升机的行驶速度;V表示救援车辆的行驶速度;E表示救援直升机的单位距离运输成本;E表示救援车辆的单位距离运输成本;d表示航空运输时点g到点h的实际距离;d'g表示公路运输时点g到点h的广义运输距离。孙华丽等用式(1)表示公路运输的广义运输距离及其对应急救援工作的影响。

道路损毁情况与复杂情况,在应急救援准备阶段进行测量,当道路无法通行时γ为无穷大。
r表示与受灾点R坐标相同的虚拟需求点集合,且r集合内所有需求点的需求量之和为f1r,i∈I,I=1,2,3,…,N;f1r表示受灾点r的最低物资需求量,受到受灾点损毁程度和当地居民人数影响;L表示受灾点r居民对满足最低需求数量的应急物资及时性感到非常满意时所能接受的最长等待时间;U表示受灾点r居民对满足最低需求数量的应急物资及时性感到非常不满意时所能接受的最短等待时间;Ω表示应急救援活动预算下限;Ω表示应急救援活动预算上限;S表示所有虚拟点集合,S=SBG∪SBG';SBG表示虚拟大需求点集合;SBG'表示虚拟小需求点集合;T表示运输方式k能从应急物流中心出发的最早时间;MT表示需求点r接收到物资的时间,r∈S;T表示受灾点r接受满足最低需求数量应急救援物资时的时间,r∈R;Q表示计划分配给受灾点r的应急物资数量;U表示应急物流中心与所有虚拟点的集合,U=S+J;t表示运输方式k将应急物资从应急物流中心送达受灾点r所耗费的时间;M表示一个大数;C表示应急物流中心的物资存量。
1.3.2 决策变量。X表示当受灾点r由应急物流中心j负责且采用公路运输时X=1,否则=0,j∈J,r∈S;Y表示当受灾点r由应急物流中心j负责且采用航空运输时Y=1,否则=0,j∈J,r∈S;P表示当有救援物资通过运输方式k运往点h时p=1,否则p=0;Q表示通过运输方式k,将应急救援物资从点g运往点h的数量,g,h∈U,k∈K;W表示应急物流中心j开启为1,未开启则为0。
1.4 数学模型
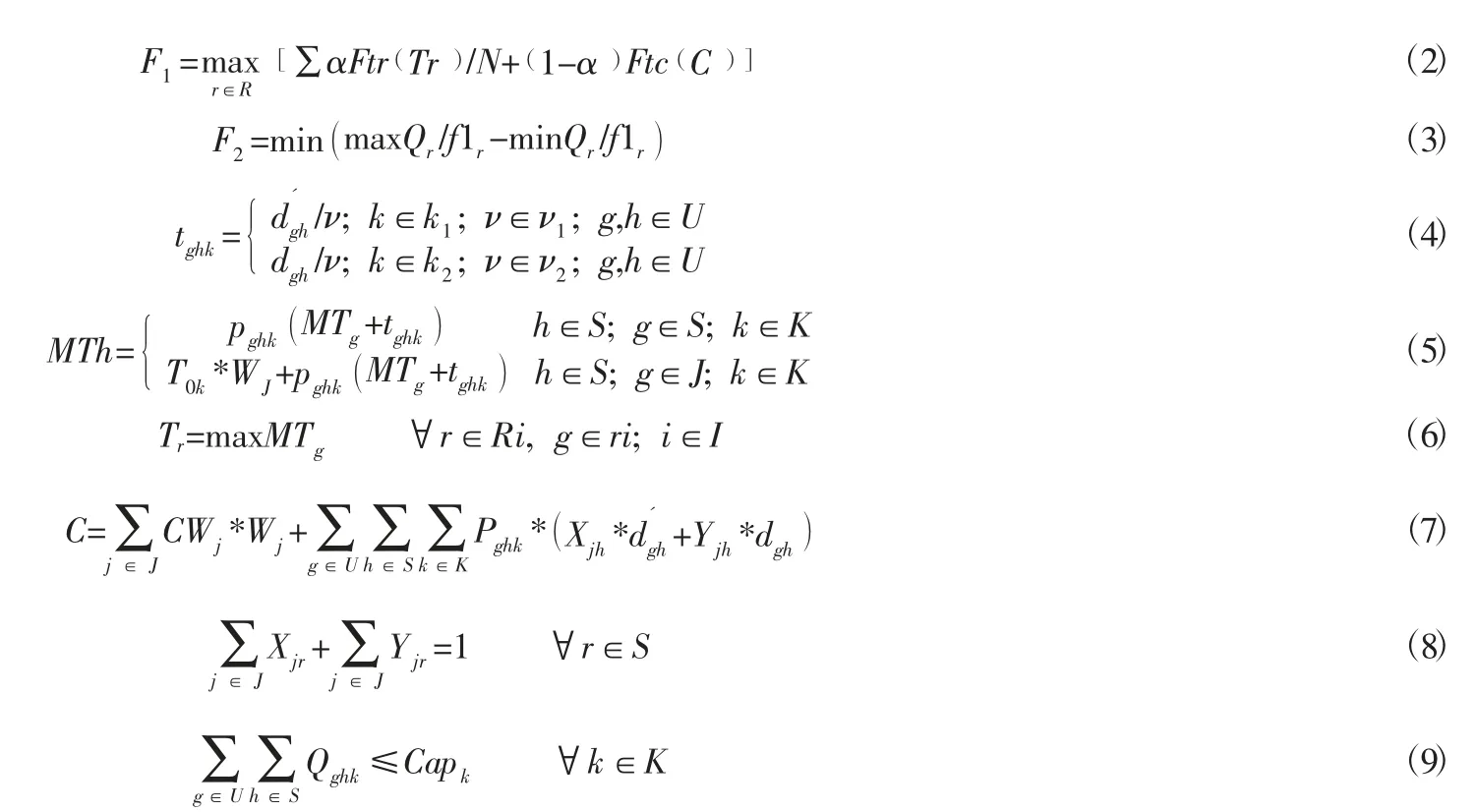

式(2)表示进行应急救援物资分配时,决策者在不同决策偏好影响下令同一度量的时间满意度与成本满意度最大。a为决策者的决策偏好。F为时间满意度函数,表示了计划应急救援物资到达时间与受灾点居民时间满意度的关系。马云峰等研究了不同情况下人们的时间满意度函数,邓斌在其基础上,定义了震后应急物流背景下的时间满意度函数如下所示:
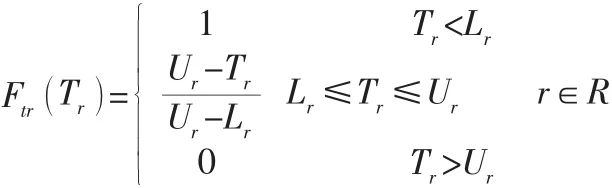
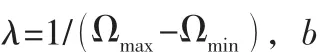

式(3)使各受灾点中对物资数量满意度最大值和最小值差值最小来最大化物资分配公平性。式(4)表示救援物资从点g到点h所耗费的时间。式(5)表示受灾点接收物资时刻的函数。式(6)受灾点接受最小物资需求量时的时刻。式(7)总应急救援成本函数。式(8)保证每个虚拟需求点只由一个应急物流中心负责,且只由一种运输方式运输。式(9)保证目标路径上的需求数量之和小于车载容量。式(10)保证开启的应急物流中心中所有物资都用于配送。式(11)保证到达受灾点r的应急救援物资大于受灾点r的最小物资需求量。式(12)保证开启的候选应急物流中心物资存量大于等于所有受灾点最低物资需求量和。式(13)保证未开启的应急物流中心没有物资配送出去。式(14)保证从应急物流中心j运出的物资小于该中心的物资剩余存量。式(15)保证车辆行驶的连续性,即驶出必定驶入。式(16)至式(18)为0~1约束。式(19)为非负约束。
2 算法设计
上述模型涉及三个目标,建立了两个目标函数,对应急救援的物资分配公平性、成本满意度、时间满意度同时进行了求解是典型的MOP问题,而MOP问题通常涉及多个目标函数,很难对解的优劣关系进行明确直接的比较,因此本文采用改进的NSGA-Ⅱ算法来确定每个个体的非支配排序等级和拥挤度来筛选优秀个体,以最终得到符合要求的最优解集。其重要操作如下:

子串2长度为P,其每个基因位取值由1~2t的自然数随机生成,t为候选应急物流中心的数目,当子串中第e个基因位的取值m能被2整除时,表示第e个受灾点由第2/m个物流中心采用航空运输方式进行配送;当取值m不能被2整除时则表示第ceil (m/2)个候选应急物流中心采用公路运输方式对第e条路径进行配送。
子串3长度为N,其每个基因位取值由1~N的自然数随机排序,表示子串1中各路径下需求点的分配顺序。
子串4长度为N,其每个基因位的取值的和为二级配送完毕后剩余物资数量,表示第三级运输的物资分配量。
2.2 染色体解码。本文为了加快算法收敛速度,使结果更优、更稳定,采用的配送方式是按照三级顺序配送方式进行的。
对此,首先要对各受灾点的需求进行处理,当受灾点的最低需求量大于单次最小运载量时,将等同于单次最低运载量的需求部分划入虚拟大需求点集合SBG。若剩余需求量小于或等于单次最小运载量时则分入虚拟小需求点集合SBG'。若剩余需求量依旧大于单次最小运载量则重复划分虚拟大需求点步骤。
2.2.1 一级配送处理。在开始第一级配送时,首先确定各虚拟大需求点的坐标位置,并根据受灾点序号按顺序依次寻找离目标受灾点最近的物流中心。对于配送时采用何种运输方式,通过综合对比物资运输时两种运输方式的时间满意度和成本满意度来进行确定。
2.2.2 二级配送处理。按照染色体中前三段的编码方式确定开启的物流中心、运输路径、运输方式等来对处于SBG'集合内的需求进行物资配送。
2.2.3 三级配送处理。第三级配送处理:由于目标函数中的时间满意度与公平性已由染色体的编码方式所确定,故三级配送主要以成本为目标进行规划。因此第三级运输的配送路径取决于以下步骤:(1)按照染色体前三段编码所给出的分配路径来确定各物流中心对剩余物资的具体分配方式,由于第三级配送以成本为导向故运输工具除无法通行外皆采用公路运输。同时按顺序遍历所有路径,确认路径i对应的物流中心j的剩余物资量是否能满足路径上所有受灾点在第四段编码中对应的预分配物资。若能够满足则路径确定,若无法满足则将无法满足的受灾点更新预分配物资后加入集合W并转入第二步。(2)按序遍历W内的所有受灾点,依次寻找离受灾点i距离最近的物流中心j,若物流中心j的剩余物资能够满足受灾点i在第四段编码中对应的预分配物资则确定该点的分配路径,若无法满足则寻找距离受灾点i下一级最近的物流中心j',直到满足受灾点i的预分配物资量并确定配送路径。
2.3 交叉变异操作。由于染色体各子串采用了不同的编码方式,因此为了保证种群多样性,子串间独立进行变异与交叉操作。子串1和子串2为范围内随机数的随机排列,采取单点交叉、双点交叉以及单点、双点变异。子串3为1~N的随机排序,采取顺序交叉与单点交叉操作。
子串4由和为固定值的随机数排列组成,为保证交叉变异后子串中各基因位值的和不变,本文采用算数交叉方法,与定量变异法进行交叉变异。算数交叉方法是指令父代两个基因位的值L、L通过公式(20)进行交叉。

3 算例分析
本文以汶川大地震受灾点分布为例构建算例,汶川大地震是我国一次造成影响十分严重的地震灾害,共涉及237个灾区,其中极重灾区10个、较重灾区41个、一般灾区186个,对震区内的人民生命与经济造成了极大伤害与损失。
3.1 数据选取。本文从极重灾区和较重灾区中随机选择15个受灾点,并在一般灾区中设置4个候选应急物流中心与一个救援飞机集散点,并按比例使其分布在100×100的平面分布图中。每个物流中心与救援飞机集散点仅有三辆运输工具。具体参数信息如表1、表2所示。其他数据由于篇幅原因不予体现。

图1 汶川大地震受灾分布图
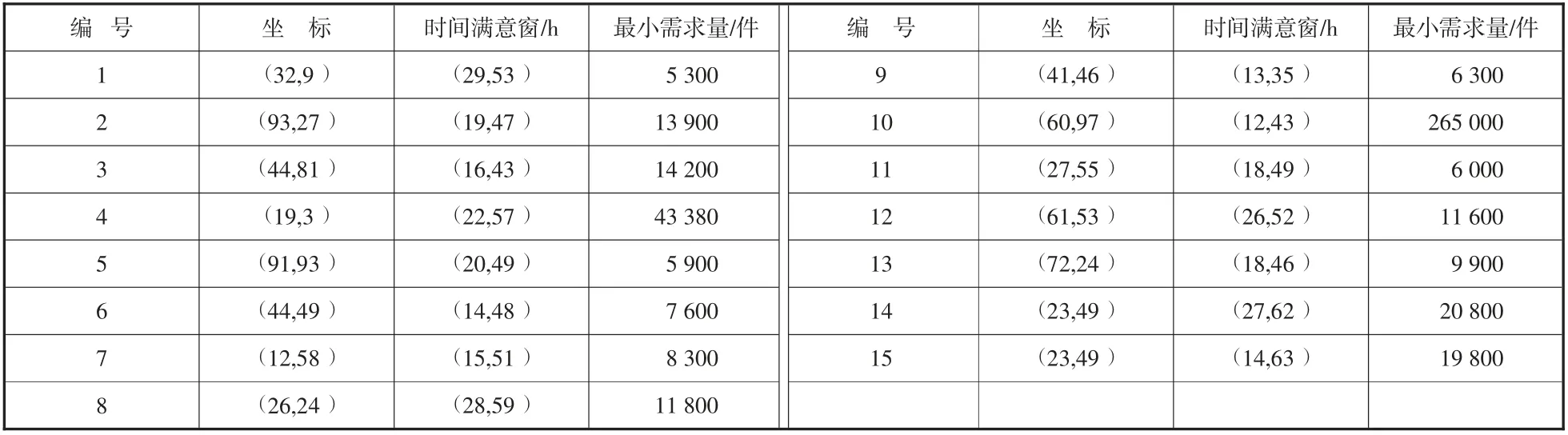
表1 受灾点需求信息

表2 候选物流中心参数
3.2 运算结果分析。NSGA-Ⅱ的参数设置如下:种群规模popsize=300,决策偏好a=0.9、最大迭代次数max gen=100,在操作系统为win10,主频为2.7GHz的Inter Core2 i5下通过MATLAB R2016a分别编写了采用分级配送与直接配送的NSGA-Ⅱ算法程序对算例进行仿真,两类算法的max gen代个体分布如图2、图3所示。表3给出了在F目标值最优时分级配送与直接配送两种配送方式求解出的具体选址—路径方案。

表3 多级配送与直接配送结果比较

图2 采用分级配送的Pareto解集
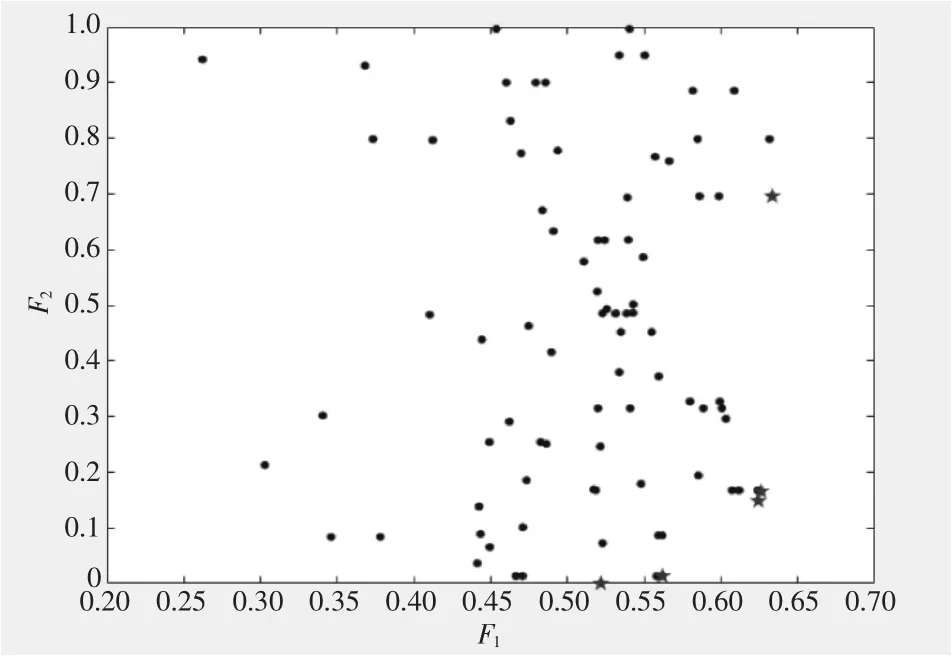
图3 采用直接配送的Pareto解集
通过图2、图3与表3的对比分析可以得出:在载具容量相差不大的情况下采用多级配送的NSGA-Ⅱ算法能够最大程度的利用当前有限的资源,包括运输工具的限制、有限的物资储备等,并在解的分布与最优解的目标值上会优于未改进的NSGA-Ⅱ算法。
4 结论
震后应急物资的分配是应急救援工作十分重要的一个环节,尤其震后初期造成的道路、公共设施损坏,不仅加大了受灾人员对救援物资的需求,同时还会对救援工作的展开造成影响。因此,为了尽可能的满足受灾人员的生理需要与心理需要,本文考虑运用航空运输与公路运输相结合的方式将初期救援物资按照设定好的三级配送方式从物资存贮点运输到受灾点,并以时间满意度、成本满意度、公平性为主要目标构建了数学模型以及改进的NSGA-Ⅱ算法对模型进行求解。
通过对改进前与改进后的求解算法进行对比分析,可以得出依据基于虚拟点的多级配送方式来设计算法会得到更优秀的Pareto解集,并且算法拥有更好的收敛性和稳定性,能为应急活动管理者提供优秀的方案以及决策支持。
在本文构建的模型中,实施应急救援工作的过程中涉及的参数是预先设定的确定数值,但在实际的救援配送过程中是动态且随机变化的。如道路安全系数、车辆的安全系数、动态变化的道路损毁程度等因素,这些动态随机的目标函数模型是未来研究的方向。

