基于改进遗传算法的主动悬架最优控制研究

陈颖

摘 要：提出了遗传-粒子群优化算法对主动悬架的控制规则进行了优化。利用Matlab/Simulink 对主动悬架系统进行了仿真，并与传统的被动悬架进行了性能比较和分析，仿真结果表明基于改进遗传算法的主动悬架最优控制能够有效提高车辆的平顺性和操纵稳定性。

关键词：LQR 主动悬架 改进遗传算法 优化设计

Abstract：A genetic-particle swarm optimization algorithm was proposed to optimize the control rules of the active suspension.Simulation study on the air suspension systems is carried out using Matlab/Simulink， and compared with traditional passive suspension in the performance comparison and analysis. Simulation results show that optimal control of the active suspension based on improved genetic algorithm can effectively improve vehicle ride comfort and handling stability.

Key words：Linear Quadratic Regulator ; active suspension; improved genetic algorithm; optimal design

悬架是指连接车身和车轮间的一切传力连接设备和装置的总称，它把车体和车轴连接起来，使他们之间具有一定的弹性[1]。根据悬架控制力大小的不同，悬架有被动、半主动和主动悬架之分。传统的被动悬架在车子行进时刚度和阻尼不能改变，面对复杂的行驶环境较难达到性能要求。主动悬架拥有可输入的外部能源，且可根据具体的道路状况和行驶状态适时地做出响应，以减小车身振动，提升行驶平顺性和乘坐人的舒适性。

在过去相当长的时间里，在主动悬架控制研究领域涌现出大量的研究者[2-5]。面对琳琅满目的控制方法，拥有二次型的性能指标的控制方法展现出了极强的优势，其只需找到合适的状态变量和控制变量的加权矩阵。遗传算法（Genetic Algorithm，GA） 是一种全局优化算法，它是通过模拟自然界生物进化的过程[6]。本文将根据遗传算法的特点将其进行改进并应用于LQR（Linear Quadratic Regulator，LQR）控制中，优化权重系数得到权重矩阵，克服根据经验确定权重矩阵，再根据响应反复调整权重系数带来的困扰，并在MATLAB平台上进行了仿真。

1 悬架

1.1 悬架模型

模型的系统运动方程见下式（1）：

式中：Mb代表簧載质量，代表车身垂向的加速度，ks代表悬架刚度，xw代表车轮垂向的位移，xb代表车身垂向位移，Ua代表控制力;Mw代表非簧载质量，代表车轮垂向的加速度，kt代表轮胎刚度，xg代表路面垂向的位移。单轮车辆模型如下图1所示：

在分析主动悬架控制过程时，本文利用白噪声信号为路面输入激励，其表达式如（2）所示

其中，f0代表下截止频率;G0代表路面不平度的系数;v代表前进过程中车速;w代表的是随机输入的均值为零的单位白噪声。

1.2 悬架评价

合理地评价一辆汽车其悬架的好坏，指标可以选择以下几个：车身垂向的加速度、悬架的动行程和轮胎的动位移，它们分别代表着乘坐舒适程度、车身的姿态和操纵的稳定性。因此，LQR控制器设计的性能指标如式（3）所示，q1，q2，q3为加权系数。

将其与系统的状态方程式   相结合得到如式（4）所示：

其中，K是一个矩阵，指的是最优控制里涉及的反馈增益，利用线性的二次最优的控制器函数[K，S，e]=LQR（A，B，Q，R，N）可以计算出K的 值;x（t）代表的实时的反馈变量;对LQR控制器进行最优控制即找到合适的q1，q2，q3，使控制器最优。下面用改进的遗传算法求q1，q2，q3。

2 改进的遗传算法

基于基本遗传算法存在初始种群的选择有一定的依赖性、早熟等不足，本文旨在引入粒子群算法（Particle Swarm Optimization，PSO 算法）[7]与基本遗传算法相混合，提高算法的运行效率。

2.1 算法设计

在进化的初期，PSO算法存在易发散、精度低等一系列的缺点，算法极易收敛到局部最优。由于PSO算法拥有较少的参数，方便调节，可以通过调节学习因子，来改变算法的全局搜索的能力。因此，将PSO算法的快速的局部的搜索能力与GA算法的全局搜索的能力相结合，设计一种新型的混合算法。具体为将混合算法分成前期和后期两个阶段：在前期，广泛利用GA的较强的全局寻优的能力，在尽可能的搜索范围里让种群获取更广的搜索规模，减小陷入局部最优的可能性。而在进化的后阶段，使用有更强社会认知的PSO算法，让其通过提升算法的局部的发掘能力，来提高算法的优化效率。

2.1.1 改进算法的框架

把GA算法和PSO群算法有效结合。n指的是改进算法中GA算法向PSO算法进行转换时GA算法进行迭代的最大次数。

2.1.2 算法中PSO算法的设计

本文对标准PSO优化算法的标准公式进行了改进，加入了一个微扰量如公式（6），来降低算法陷入停顿的可能性。

式中，R1是一个随机数，它的取值的范围可以在[-1，1]之间。t是正数，它的取值的范围可以在（0，1]之间，且与迭代次数的变化息息相关。

2.1.3 算法中遗传算法的设计

（1）编码

采用实数编码，为的是方便后期与PSO算法进行混合地编码。

（2）初始种群的产生

可行解与不可行解空间共同产生初始种群。可行解空间[L，U]上，随机生成初始个体Xi（0） （i=1，2，…，pop），这pop个个体是均匀分布的;在不可行解空间Q上，随机生成初始个体X i（0）（i=pop+1，…，pop+N2），这N2个个体也是均匀分布的。其中，pop为种群规模，N2为不可行解数量，且pop>N2。

（3）交叉算子

采用单点交叉方式。

（4）变异算子

采用随机两点位置进行变换，生成随机数字λ1、λ2，其取值范围是1到10之间的整数。

（5）适应度函数

把优化问题取最小值优化，在该问题中评价主动悬架的适应度函数如式（7）所示：

其中，BA代表的是车身垂直加速度的均方根值，SWS代表的是悬架动行程的均方根值，DTD代表的是车轮动位移的均方根值，BApas代表的是被动悬架的车身垂直加速度的均方根值、SWSpas代表的是悬架动行程的均方根值、DTDpas分别代表的是轮胎动位移的均方根值。

（6）选择操作

将父代的种群、交叉后的子集和变异后的子集进行合并，其为了减少子代返祖的可能性，应将交叉和变异以后的子代个体进行甄别，如果其已经在父代中出现，应给予剔除。在选择的时候采取精英保持的战略，把父代与子代进行归并，有效减小子代的退化，同时把交叉和变异后得到的个体与子代归并，以增加种群的多样性。在这个种群中，可以选取适应度排序在前pop个的单独个体，并选做下一代种群。

2.2 算法流程

Step1：根据优化区间，初始化群体;

Step2：把种群中的每一个个体值一次给予LQG控制器的q1，q2，q3。然后运转控制系统中建立的Simulink模型，以获取悬架的性能指标。

Step3：根据种群中不同个体的适应度函数取值差异，依此判别遗传算法是否终止。若满足遗传算法终止条件，则退出;否则进行Step4。

Step4：根据当前迭代次数iter值进行判断，若不大于n，则进行遗传算法的迭代;若大于n则进行粒子群算法迭代。

3 结果分析

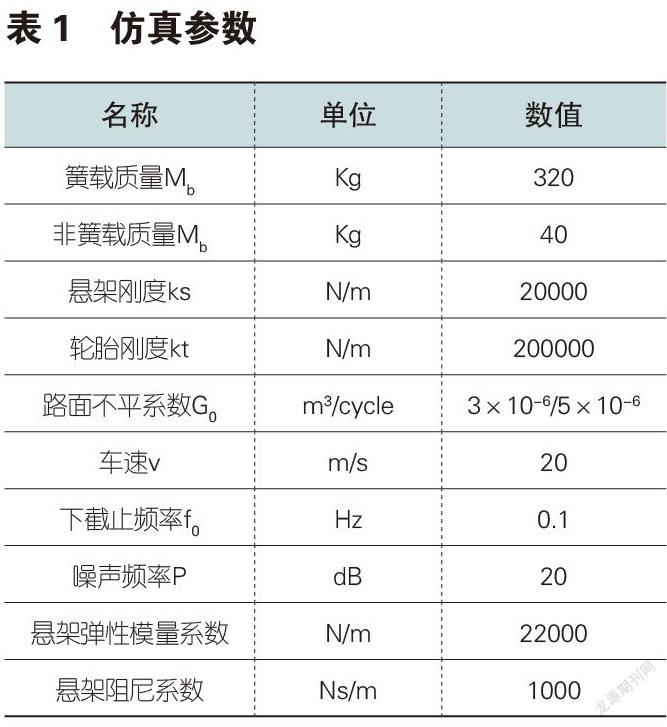
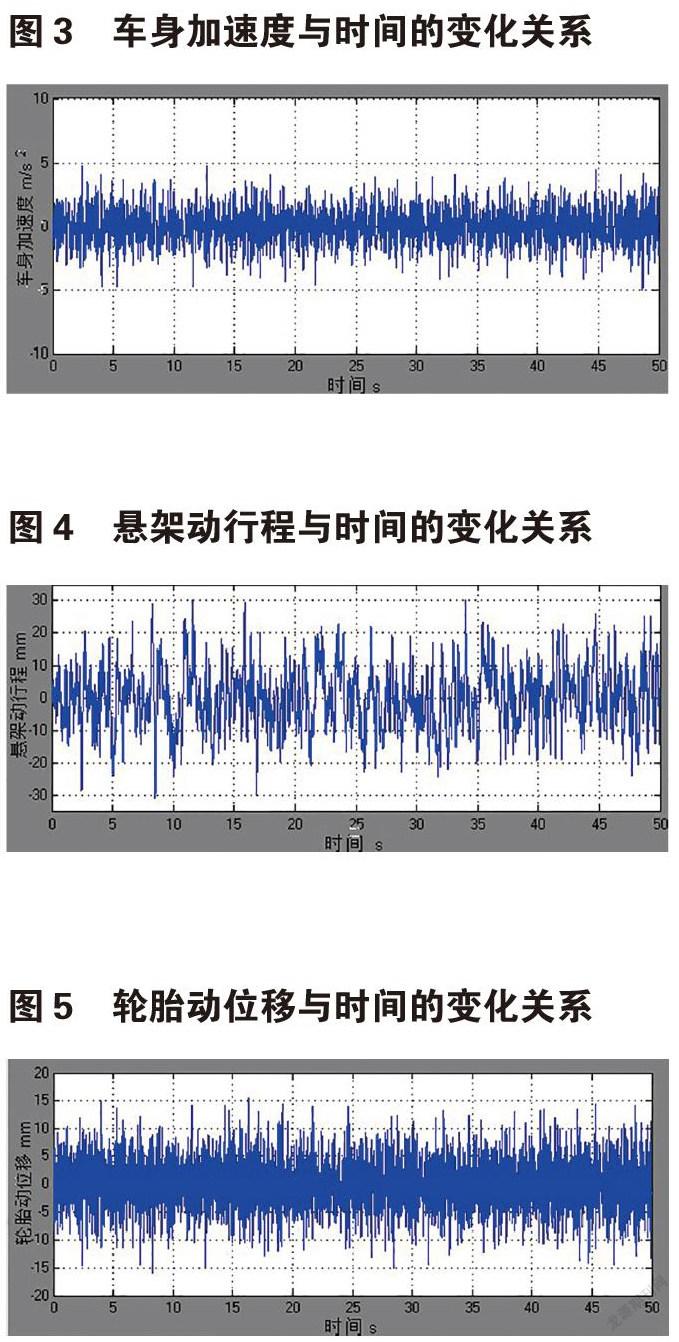
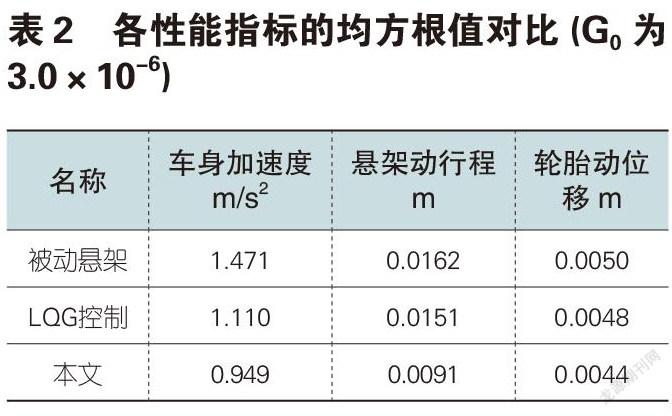
利用Matlab软件中的Simulink工具，建立控制系统的仿真模块，并依据此进行仿真，如图2所示，其中输出依次为车身垂向的加速度，悬架的动行程，轮胎的动位移。仿真的参数设置按照表1进行，模块[t，w]是路面输入白噪声。

在遗传-粒子群优化算法中，取遗传算法的种群规模为pop=100，N2=20交叉概率pc=0.8，变异概率pm=0.2，最大迭代次数GMAX=100，n=50。粒子群算法的参数c1=0，c2=2。

在不平系数为3×10-6的路面上，对模型进行仿真，得到的结果如图4-6所示。此时的最优个体q1=121341，q2=9422，q3= 311054。

文中选用：车身加速度、悬架动行程和轮胎动位移，且在一样的仿真环境下选取被动悬架和常规LQG控制器作比较分析，见表2。

由图3-5和表2得出基于改进遗传算法（遗传-粒子群优化算法）的控制器使得主動悬架的性能指标与被动悬架和LQG控制的悬架性能指标相比，具有明显的优势。当路面不平系数为3.0×10-6时，本文用遗传-粒子群优化算法得到的车身加速度的均方值，与LQG和被动悬架相比，分别减少了24%和34%。

用遗传-粒子群优化算法得到的悬架动行程和轮胎动位移较LQG和被动悬架也有大幅度的提升。本文所用方法有效地提升了汽车行驶平顺性和操纵稳定性。仿真结果证明基于遗传-粒子群优化算法的优化是有效的。

4 结论

本文利用遗传-粒子群优化算法对LQG控制器进行了优化，为主动悬架LQG控制器的加权系数的确定提供了一种方法，减少了加权系数设置的盲目性，提高了效率; 基于改进遗传算法（遗传-粒子群优化算法）的主动悬架可以很好地降低车身的加速度，提升乘坐人的乘坐体验感和舒适度，适应性和鲁棒性较好，而且控制的方式相对便捷，利于实施。

基金项目：2020年校科技工程项目《基于遗传算法在汽车悬架中的应用与研究》（azy2020kj06）;2021年提质培优项目《新能源汽车技术》课程思政教育案例2021xjtz071;2021年提质培优项目精品在线课程《纯电动汽车电机及传动系统检修》2021xjtz050;2021年提质培优项目具有职业教育特点的课程思政教育典型案例的研究与实践——以《新能源汽车技术》为例 2021xjtz043。

参考文献：

[1]Yu F，Corolla D A. An optimal self-tuning controller for an active suspension [J]. Vehicle system dynamic，1998，29： 51-65.

[2]舒红宇，李伟，何渝生.汽车主动悬架的理论分析及模型试验[J].汽车工程，1991（3）：129-135.

[3]郭建华，李幼德，李静. 基于遗传算法的主动悬架模糊控制器设计[J]. 系统仿真学报，2007，19（18）： 4178-4181.

[4]王亚雄，蔡宇萌，王健，姚明，陈士安.汽车侧倾运动安全主动悬架LQG控制器设计方法[J].交通运输工程学报，2017，17（05）：138-148.

[5]陈丽静.基于Matlab最优控制主动悬架对汽车侧翻稳定性仿真分析[J].黑龙江工程学院学报，2019，33（06）：40-46.

[6]Holland J H. Adaptation in natural and artificial systems： An introductory analysis with applications to biology，control，and artificial intelligence[M]. U Michigan Press，1975.

[7]Kennedy J，Eberhart R. Particle swarm optimization[C]//Proceedings of IEEE international conference on neural networks. 1995，4（2）： 1942-1948.