8 bit量化误差对正弦参数拟合影响的误差界

梁志国

(北京长城计量测试技术研究所 计量与校准技术重点实验室，北京 100095)

1 引 言

正弦现象是自然界中的基本物理现象之一，涉及到振动、摆动、波动的多数现象，均可以归结为正弦现象。因而，正弦波成为仪器仪表和计量测试行业中应用最广的曲线波形[1～5]。以正弦波形采样序列为基础的四参数最小二乘曲线拟合算法，成为估计正弦波形的幅度、频率、初始相位、直流偏移4个基本参数的最精确方法，应用广泛[6～9]。它可适用于单周期、多周期、残周期、均匀采样、非均匀采样等多种不同的测量条件[2,3,7,8,10～12]。不仅如此，它还被用于A/D的有效位数评价中，成为必不可少的基本方法[6,9,13～15]。在调制信号的数字化解调，以及其它许多相关问题的解决中，均有重要应用。

在正弦波形参数拟合中，人们最关心拟合参数的不确定度或误差状况[14～21]。针对这一问题，美国NIST的Deyst等进行了先期研究[16]，其主要涉及的因素包括谐波、抖动、信噪比、初始相位、序列所包含的周波数、序列长度等几个因素，及它们对幅度、频率、初始相位、直流分量4个拟合参数的影响；并以经验公式、仿真曲线方式，给出了这些因素产生影响的误差界，对实际工作具有较大的指导和借鉴价值，意义重大。然而，量化误差的影响并未予以特别关注。实际上，正弦波采样序列多是通过A/D转换器以模数转换实现模拟信号向数字量的转化。目前，已有的模数转换器技术产品，A/D位数已经覆盖了8～24 bit分辨力的全部范围，并已经有32 bit分辨力的A/D产品出现。但是，大多数数字示波器的A/D位数仍然使用8 bit分辨力的A/D，因此，量化误差的影响不容忽视。

量化误差并非随机误差，在周期性波形的测量中，它是兼具系统误差和噪声误差特性的周期性误差因素。首先，它会给幅度拟合带来随幅值变化而变化的影响，并间接影响到其它参数的拟合结果。

另外，即使是同一幅度的正弦信号，由于叠加在其上的直流分量(直流偏移)不同，也会导致量化后的采样序列量化误差的变化。

最后，在确定的A/D位数基础上，变化的信号幅度、频率、初始相位，以及变动的采样速率、序列长度、序列所含的周波数等因素发生变化时，都将给正弦波拟合参数带来怎样的变化，这些状况，尚未予以系统揭示。

实际上，在许多场合下，和谐波、随机噪声等因素相比，A/D量化误差、信号量程、采样速率、序列长度等测量条件起到了主导作用。但每一次测量，所面临的波形参数，所使用的测量条件等又具有非固定的特征。在这种情况下，人们更为关心的是，存在A/D量化误差的情况下，每一种不同的测量条件下四参数正弦曲线拟合参量的误差界变化情况，以便指导测量仪器系统的选用，构建测量条件，从而达到预期的测量目的。本文后续内容，将主要讨论量化误差带来的拟合参量的误差界问题，并试图以仿真计算方式，针对8 bit分辨力A/D的情况，将每一种组合方式的误差界揭示出来。

2 基本思想

2.1 测量条件

在波形数据采集中，测量条件通常涉及主观条件和客观条件2种。客观条件一般指被测波形的参量条件, 包括幅度、频率谱等信息。对于正弦信号，则指其幅度、频率、直流分量、初始相位等波形参量；更进一步细化，将包括其抖动、失真、谐波、噪声等等参量；它们是不以人的意志为转移的客观存在，很难被干预和变动。主观条件，则特指可以通过自主选择而变化的测量条件，包括测量仪器系统的幅度量程、A/D位数、采样速率、存储深度、通频带、幅度测量误差、线性度、采样速率误差等。

在正弦波形的采样测量中，采样速率与信号频率是相关联的，两者的比值是每个周波的采样点数，通过选择不同的采样速率而改变该比值；当其固定后，采样序列的长短决定了其所包含周波数的多少。通过选取量程范围，改变被测信号幅度与量程的占比；通过选择不同A/D位数的测量仪器和系统，改变量化误差的大小。最终，用于改变正弦波拟合参数的误差界。

综合考虑各方面因素，选出具有相互独立性和系统完备性的左右量化误差影响的测量条件为：

1)A/D位数，用于确定量化水平及影响；

2)采样序列包含周波数，用于确定周波数的影响；

3)序列样本点数，用于确定存储深度的影响；

4)信号幅度，用于确定幅度变动的影响；

5)初始相位，用于确定信号相位变化带来的影响；

6)直流分量，用于确定直流分量变化带来的影响。

经过四参数正弦曲线拟合后，获得的指标特征参量为：

1)有效位数误差界，单位为bit。有效位数通常用以表述拟合曲线和实际测量序列之间的拟合残差，假定其在整个信号量程范围内均匀分布，按照纯量化误差规律折合成的A/D位数。理想状况下，有效位数的量值应该与测量序列所用的A/D位数相等；其误差界，应该是有效位数不确定度的波动边界。

2)拟合幅度误差界，以LSB表述。

3)拟合频率误差界，以相对误差表述。

4)拟合相位误差界，单位以度(°)表述。

5)拟合直流分量误差界，以LSB表述。

LSB(least bit)称为最小量化阶梯，当A/D位数为b，幅度量程为E时，有

2.2 误差界搜索

正弦参数拟合的误差界，是在上述6项测量条件下，固定其中的5项，变化1项，搜索出该条件变化时，四参数正弦拟合所获得的有效位数、幅度、频率、相位、直流分量等5项指标的误差界。

3 仿真实验及数据处理

仿真使用计算机进行，按照数学关系产生理想正弦数据，然后再设定量程，按照仿真的A/D位数进行量化，生成理想仿真序列。将该具有已知参量的仿真序列在选定的正弦波拟合软件中进行数据处理，获得拟合参数。

仿真参数按照已知规律变化，获得变化条件下的拟合参数变化规律，并以此搜索各个拟合参数的误差界。

3.1 仿真实验条件

为方便参数调控，不失一般性，设定包含6项测量条件的仿真实验条件如下：

1)A/D位数，基本参量为8 bit。

2)采样序列包含周波数，未特别说明时，为20个周波。作为主变化因素时，变化范围为0.90～21.00个周波，0.01周波步进；作为辅助变化量时，变化范围为2～20个周波，1周波步进。

实际仿真过程中，通过使用归一化频率1 Hz来调整采样速率，结合样本点数，最终构建周波数。

3)序列样本点数，未特别说明时，序列样本点数为16 000点。

作为主变化因素时，变化范围为100～16 000点，1点步进；作为辅助变化量时，变化范围为 1 000～16 000点，1 000点步进。

4)信号幅度，使用归一化幅度1。未特别说明时，幅度为82.312 5%×量程，并以此设定量程范围。

作为主变化因素时，幅度宏观变化范围为量程的7.8%～100%，0.005 LSB步进；作为辅助变化量时，在82.312 5%×量程点处，其微观变化范围-0.5～0.5 LSB，0.05 LSB步进。

5)初始相位，未特别说明时，初始相位为0°。

作为主变化因素时，变化范围为-180～180°，1°步进；作为辅助变化量时，范围不变，10°步进。

6)直流分量，未特别说明时，直流分量为0。

作为主变化因素时，变化范围为-2～2 LSB，0.01 LSB步进；作为辅助变化量时，变化范围为-0.5～0.5 LSB，0.05 LSB步进。

3.2 仿真实验结果

按照上述仿真实验条件，分别以一种参量为主变化因素，另一种参量为辅助变化因素生成实际的仿真条件，考察各指标要素的误差变化情况。

3.2.1 幅度作为主变化因素

1)周波数作为辅助变化量，获得如附录中图1所示的误差变化曲线波形。

2)相位作为辅助变化量，获得如图2所示的误差变化曲线波形。

3)直流分量作为辅助变化量，获得如图3所示的误差变化曲线波形。

4)数据点数作为辅助变化量，获得如图4所示的误差变化曲线波形。

3.2.2 周波数作为主变化因素

1)幅度作为辅助变化量，获得如图5所示的误差变化曲线波形。

2)初始相位作为辅助变化量，获得如图6所示的误差变化曲线波形。

3)直流分量作为辅助变化量，获得如图7所示的误差变化曲线波形。

4)数据点数作为辅助变化量，获得如图8所示的误差变化曲线波形。

3.2.3 初始相位作为主变化因素

1)幅度作为辅助变化量，获得如图9所示的误差变化曲线波形。

2)周波数作为辅助变化量，获得如图10所示的误差变化曲线波形。

3)直流分量作为辅助变化量，获得如图11所示的误差变化曲线波形。

4)数据点数作为辅助变化量，获得如图12所示的误差变化曲线波形。

3.2.4 直流分量作为主变化因素

1)幅度作为辅助变化量，获得如图13所示的误差变化曲线波形。

2)周波数作为辅助变化量，获得如图14所示的误差变化曲线波形。

3)初始相位幅度作为辅助变化量，获得如图15所示的误差变化曲线波形。

4)数据点数作为辅助变化量，获得如图16所示的误差变化曲线波形。

3.2.5 数据点数作为主变化因素

1)幅度作为辅助变化量，获得如图17所示的误差变化曲线波形。

2)周波数作为辅助变化量，获得如图18所示的误差变化曲线波形。

3)初始相位作为辅助变化量，获得如图19所示的误差变化曲线波形。

4)直流分量作为辅助变化量，获得如图20所示的误差变化曲线波形。

3.3 仿真实验结果分析

3.3.1 有效位数误差界

从图1(a)～图20(a)可以看出：

1)数据点数是影响有效位数误差界(误差包络线)的最重要因素，总体而言，数据点数的增大，可以导致有效位数误差界的变窄，但并非单调变窄。500点以上的数据点数，可以获得有效位数误差界下界-0.5 bit，上界0.5 bit；更窄的误差界需要更多的数据点数。

2)当幅度在量程范围内大尺度变化时，有效位数误差界随幅度增加呈缓慢下降趋势；当幅度量程比在7.8%以上时，其误差下界-0.1 bit，上界0.1 bit；幅度在LSB量值尺度的微小范围变化时，有效位数误差随幅度变化呈局部周期性变化，幅度周期为1 LSB；在满量程附近会出现削波影响导致的有效位数误差增大现象。

3)有效位数误差随周波数的增加呈震荡衰减变化。其波动的误差下界-0.01 bit，上界0.01 bit。

4)初始相位因素对有效位数误差的影响可以忽略。其波动的误差下界-0.000 3 bit，上界0.000 3 bit。

5)直流分量在LSB量值尺度的微小范围变化时，有效位数误差随其变化呈周期性变化，幅度周期为1 LSB；其波动的误差下界-0.022 bit，上界0.018 bit。

3.3.2 幅度误差界

从图1(b)～图20(b)可以看出：

1)数据点数是影响幅度误差界的最重要因素，数据点数的增大，可以导致幅度误差界的单调变窄。其误差界下界-0.53 LSB，上界0.52 LSB；更窄的误差界需要更多的数据点数。

2)幅度误差界随幅度增加呈缓慢下降趋势，下界-0.12 LSB，上界0.06 LSB。

幅度在LSB量值尺度的微小范围变化时，幅度误差随幅度变化呈局部周期性变化，变化周期为1 LSB；不同幅度将改变幅度误差的量值。

3)周波数为2及以上时，周波变化给幅度误差界带来的影响可以忽略。当周波数为1时，幅度误差界有显著性增大(下界-0.15 LSB，上界0.07 LSB)。

4)初始相位因素的影响可以忽略。

5)幅度误差界随直流分量的变化呈周期变化，周期为1 LSB，其下界-0.037 LSB，上界0.012 LSB。

3.3.3 频率误差界

从图1(c)～图20(c)可以看出：

1)数据点数与周波数的结合，是影响频率误差界的最重要因素，数据点数的增大，可以导致频率误差界的变窄，但并非单调变窄。100点以上的数据点数，可以获得频率误差界下界-1.3×10-3，上界1.3×10-3；更窄的误差界需要更多的数据点数。

2)频率误差随幅度增加呈衰减下降趋势，但不单调下降，主要由幅度、周波数的变化确定，下界-2.6×10-4，上界4.0×10-4。

3)周波数增大时，频率误差随周波数增加呈震荡衰减趋势，但并不一直单调下降，频率误差下界-3.2×10-4，上界2.0×10-4。

4)初始相位、直流分量因素的影响可以忽略。

3.3.4 初始相位误差界

从图1(d)～图20(d)可以看出：

1)数据点数与周波数的结合，是影响初始相位误差界的最重要因素，数据点数的增大，可以导致初始相位误差界的变窄，但并非单调变窄。其误差界下界-0.24°，上界0.24°；更窄的误差界需要更多的数据点数。

2)初始相位误差随幅度增加呈衰减下降趋势，但不单调下降，主要由幅度、周波数的变化确定，下界-0.10°，上界0.12°。

3)当周波数为1.4以上后，初始相位误差界比较平稳，下界-0.067°，上界0.077°；在周波数较低时，会有较大跳变。

4)初始相位误差界，随初始相位本身、直流分量等各种因素影响而变化的规律均比较平稳。下界-0.005°，上界0.005°。

3.3.5 直流分量误差界

从图1(e)～图20(e)可以看出：

1)数据点数是影响直流分量误差界的重要因素之一，数据点数的增大，可以导致直流分量误差界的变窄，但并非单调变窄。其误差界下界-0.33 LSB，上界0.40 LSB；更窄的误差界需要更多的数据点数。

2)0值的直流分量误差界随幅度增加呈缓慢上升趋势，主要由于幅度上升后，接近0值的直流分量与其相差悬殊，运算舍入误差造成；下界-0.002 4 LSB，上界0.002 4 LSB。

非0值的直流分量误差界量值由幅度、直流分量组合变化确定，下界-0.044 LSB，上界0.044 LSB；且随着幅度大尺度上升，误差界呈震荡衰减变化。

在满量程附近出现的削波影响也有导致直流分量误差增大现象。

3)同一周波数，直流分量误差界变化的规律为随幅度增加呈缓慢上升趋势；而不同周波数时直流分量误差界有显著不同，并无单调趋势。

特例，当周波数为1时，幅度直流分量误差界有显著性增大(下界-0.080 LSB，上界0.044 LSB)；且误差界变化的规律为随幅度增加呈缓慢下降趋势。

4)初始相位因素对直流分量误差的影响可以忽略。下界-0.002 LSB，上界0.002 LSB。

5)直流分量在LSB尺度的微小变化将导致其自身误差较大变化，局部具有周期性特征，以1 LSB为周期，下界-0.008 3 LSB，上界0.008 1 LSB。

3.3.6 正弦拟合参数的条件误差界

8 bit A/D转换器正弦拟合参数的条件误差界如表1所示。

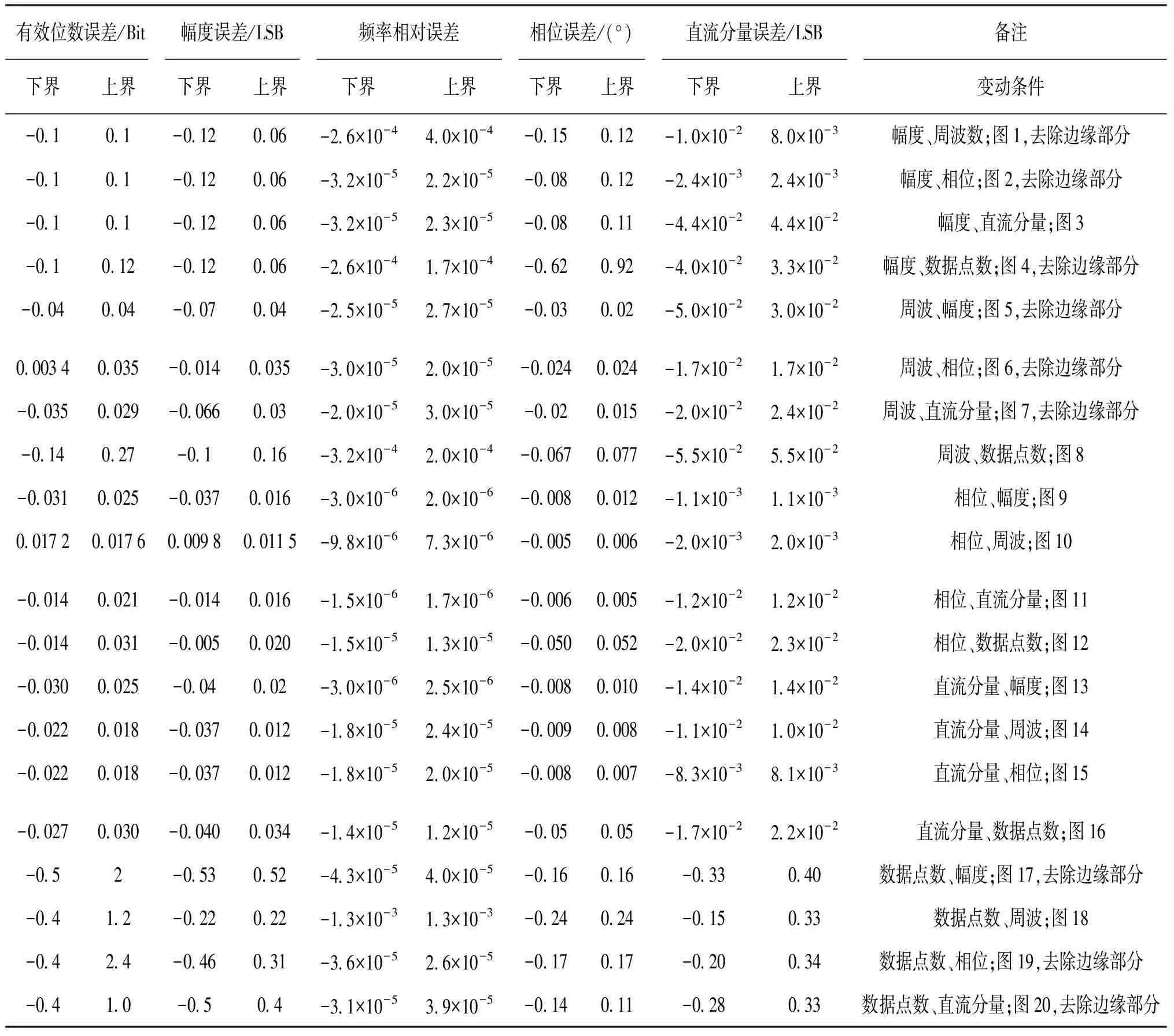
表1 正弦拟合参数的条件误差界(8 bit A/D)

4 问题讨论

本文上述过程，是提取出幅度、周波数、相位、直流分量和数据点数作为变动参量，使用有效位数误差、幅度误差、频率相对误差、相位误差和直流分量误差作为正弦拟合结果的指标参量。并以其中每一参量作为主变动因素，其它四项参量作为辅助变量的情况进行了二维搜索，揭示了双变量组合变化情况下的各个指标参量误差界的变化情况，获得了不同组合实验条件下的误差界测量曲线。结果表明：

1)拟合序列的数据点数仍然是最重要的测量条件，也是影响拟合结果的误差界的主导条件；若想获得更高准确度的拟合结果，通常需要更多的数据点数。就本文所述的有20个周波的测量序列而言，13 500点以上的数据点数可以获得最良好的拟合结果。

对于随机噪声的影响而言，拟合序列的数据点数的增加，可以导致拟合结果误差界的单调下降；而本文的实验表明，对于量化误差的影响而言，并未完全呈现出同样的单调规律，具体原因需要将来进一步研究予以解决。

2)波形幅度是指其相对量程范围的占比而言，实验表明，幅度量程比为1/2、1/3、1/4、1/5、1/6、1/7、1/8、1/9、1/10、1/12的幅值点附近，拟合频率误差和拟合相位误差均较大，原因不明，需要进一步研究予以解决。

超过半量程以后幅度的信号波形，其拟合误差界趋于平稳。因此，测量活动应尽量选择半量程以上覆盖率的幅值进行。

3)周波数的影响实际上体现的是采样速率和信号频率比的影响。实验表明，只有频率拟合误差随周波数的增加呈震荡衰减趋势，并且周波数越小，变化趋势越显著，在10个周波以后的变化趋势趋于平稳。

非整数的周波数变化，会给有效位数误差带来小幅波动；其它参量随周波数没有明显趋势性变化。若想获得较小的拟合误差，则应适当提高拟合序列周波数，至少应为2个周波以上；和多周波条件相比，1.3个以下的周波数将使得拟合误差显著升高。

4)初始相位的变化，对每一个参量拟合的影响都处于可以忽略的微小状况，且误差带平稳。其对于有效位数误差带的影响约为±0.000 25 bit；对于幅度拟合误差带的影响约为±0.001 LSB；对于初始相位拟合误差带的影响约为±0.006°；对于直流分量拟合误差带的影响约为±0.002 LSB。

5)直流分量的变化，本文只关注到了LSB量值范围的变化带来的影响。在该尺度上，它的变化给每一个参量的误差带均带来周期性影响；给其它参量误差带的影响均呈现明显的对称性，而给直流分量本身误差带的影响则具有反称性特征。

6)本文实验开始时，曾经试图通过选取信号幅度寻找出幅度误差为0的幅度点，从幅度与直流分量联合变换获得的幅度误差带曲线可见，不存在误差界宽度为0的幅值与直流分量组合点存在。只要幅度和直流分量出现一个量不可控，就无法保证获得的采集波形幅度误差为0。从实验方案中试图构建幅度误差为0的测量条件是不可能的。

7)如果在实际工作中，并不需要获得全部上述5个参量，而仅仅需要其中某一个参量的高精度结果，例如有效位数，则可以根据该参量的影响因素显著程度，只注意调控和构建所需要的影响量条件即可，其它可以自由选取，不必全盘考虑，将使得实验设计更容易。

5 结 论

综上所述，本文通过大量仿真实验，对使用8 bit A/D转换器测量系统所得的正弦测量序列，在波形拟合中获得的幅度、频率、初始相位、直流分量和有效位数5个参数的拟合误差界进行了搜索研究，给出了误差界随波形幅度、周波数、初始相位、直流分量、数据点数等不同组合条件而变化的曲线，揭示出其变化规律。例如拟合误差随幅度宏观上升变化而呈现出的总体下降趋势，随幅度和直流分量在LSB尺度的微小变化呈现出的周期性变化规律；随周波数、数据点数上升而呈现出的总体下降趋势；并发现了误差规律随幅度、周波数、数据点数上升过程中的非单调现象；总结出了显著影响量和非显著影响量。对正弦拟合参量的不确定度评估和误差界定具有重要意义和价值。另外，对于拟合参数误差有明确要求的场合，可以通过构建相适应的测量条件获得预期结果。

由于绝大多数数字示波器使用8 bit A/D转换器，正弦拟合越来越成为高精度测量分析的重要手段；因此，本文的获得的结论将拥有广阔的实际应用前景。