船舶停靠码头撞击力研究

周 丹

（重庆交通大学河海学院，重庆400074）

引言

三峡大坝建成运行以来，三峡库区水运规模不断扩大，必然的带动船舶的大型化，提高了大型船舶进出港的频率，同时靠泊撞击力的增大增加了码头被撞毁的可能性，因此水运交通的快速发展对码头要求逐渐提高。由于大型化码头受到相关条件的限制没有得到过多新建，来往船舶不得不停靠老旧码头，而内陆码头多修建于多年以前，其设计靠泊能力较低，加上码头运行多年，受大气水流的冲刷腐蚀、船舶的低频撞击，码头疲劳损伤逐年累积，其结构承载性能降低，导致既有码头结构远不能达到现有航运靠泊能力需求。因此常出现大型化船舶超限停靠老旧码头，在靠船墩处造成过大撞击力，严重影响老旧码头安全运行的情况，降低码头剩余寿命，这与航运飞速发展之间的矛盾日益突出。因此，在船舶大型化的背景下，研究大吨位船舶停靠内河既有架空直立式码头过程撞击力对码头的影响具有十分重要的意义。本文利用ABAQUS 建立精细化有限元模型，对不同吨位、不同初始速度、不同撞击角度的船舶停靠码头的过程进行数值仿真分析，研究码头所受撞击力变化情况，为后期码头防撞的研究提供指导作用。

1 有限元理论与求解

船舶停靠码头时与靠船墩的低速碰撞使得结构发生非线性动态变化[1]，碰撞过程动力响应十分复杂，由于计算机等软硬件设备的发展与成熟，计算机有限元分析方法可以十分有效的分析碰撞过程中的非线性问题。有限元分析是利用数学近似的方法来模拟真实的静态或动态过程的物理物体或体系，其基本思想可以概括为以下几个步骤：

1）把结构理想化为仅靠节点相互连接的有限单元的集合体，在节点处定义自由度u。

2）对每个有限单元，形成关于单元自由度的单元刚度矩阵ke，单元质量矩阵me，单元作用力向量pe(t)，对于每个单元，假设用节点位移表示的单元位移场，则力-位移关系及惯性力-加速度关系为：

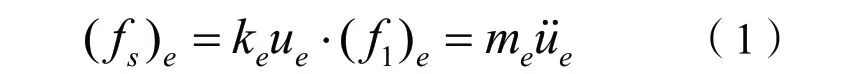
3）形成转换矩阵ae，建立单元位移ue、单元力pe(t)与有限单元几何体的位移u及力p的关系：

式中：ae是由0 和1 组成的布尔矩阵，它把ke、em、pe的元素定位于有限单元集合体的刚度矩阵、质量矩阵和作用力向量中的正确位置。

4）集装单元矩阵，形成有限单元集合体的刚度矩阵、质量矩阵和作用力向量：

A代表直接组装过程，从1 到Ne的每个单元（Ne的是单元个数），按照ae分别集装单元刚度矩阵、单元质量矩阵和单元力向量，形成整体刚度矩阵、整体质量矩阵和整体力向量。

5）建立有限单元集合体的运动方程：

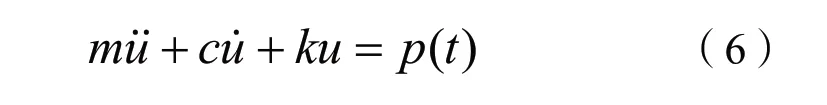
式中：c为阻尼矩阵

有限元分析用较简单的问题代替复杂体系问题后再求解，将复杂的工程问题进行简化，且能适应各种复杂形状，并能得到精度较高的近似解，因而成为应用广泛、行之有效的工程分析手段。

2 有限元模型的建立

2.1 工程背景

某码头工程河段河道呈微弯形态，港区位于深水区的弯道凹岸。河床与岸坡稳定，枯水期最小水深一般可以维持在3 m 以上，汛期可达30 m 以上。码头属于已建的内河高桩架空直立式码头，且为件货码头。港区年水位落差大，洪峰变幅大、历时短，而枯水期水位平稳、历时长。设计洪水频率为5/100，设计最高洪水位为186.30 m，最低通航水位为158.02 m。

2.2 船舶模型

该码头原设计靠泊船舶吨位3 000 DWT，本文选取以下三种船舶作为本论文的计算船舶，其主要尺寸如表1 所示：

表1 码头停靠船舶主尺度

本文全船利用壳单元建立简化的船舶模型，包括船甲板、底板、外板、内板、肋板，使得船舶模型与实际船舶的刚度、密度、质量保持一致。船舶与浮箱接触部位网格控制在0.2 m，其余部分网格控制在0.5 m 范围内，将船舶质量均匀分布在船身单元，船体单元共40 948 个，有限元模型如图1 所示，本模型中停靠船舶材料为Q235 钢板，有限元模型采用随动强化弹塑性模型，材料参数如表2 所示。

图1 停靠船舶有限元模型

表2 停靠船舶模型主要参数

表中：ρ为材料密度，Es为弹性模量（MPa），μ为泊松比，σY为屈服应力，Et为切线模量。

2.3 码头模型建立

码头由面板、横纵梁、横纵联系撑、斜撑、靠船墩组成。码头模型用实体建模，由于该码头具有对称性，因此建立码头一半的11 个排架进行计算分析，得到简化的线弹性材料的实体单元码头模型，网格控制在0.5 m，单元共382 439 个。码头的有限元模型[2]如图2 所示，码头采用材料为C35 混凝土，本构模型采用混凝土损伤塑性模型，其材料参数[3]见表3 所示：

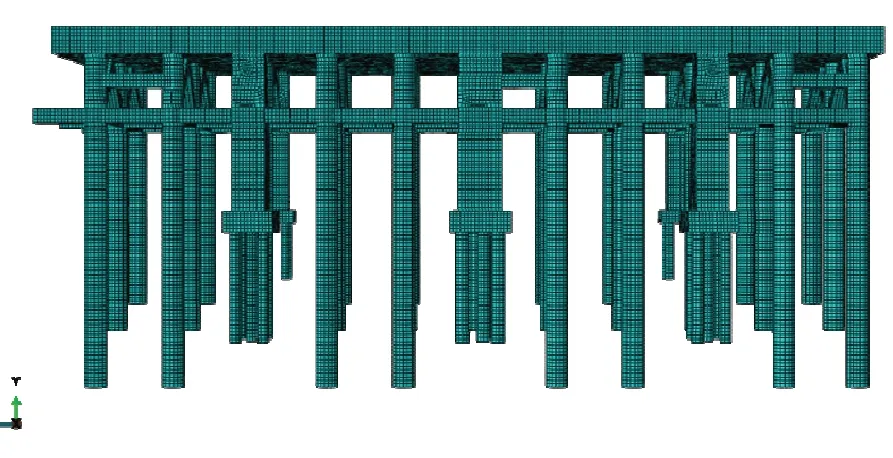
图2 码头的有限元模型

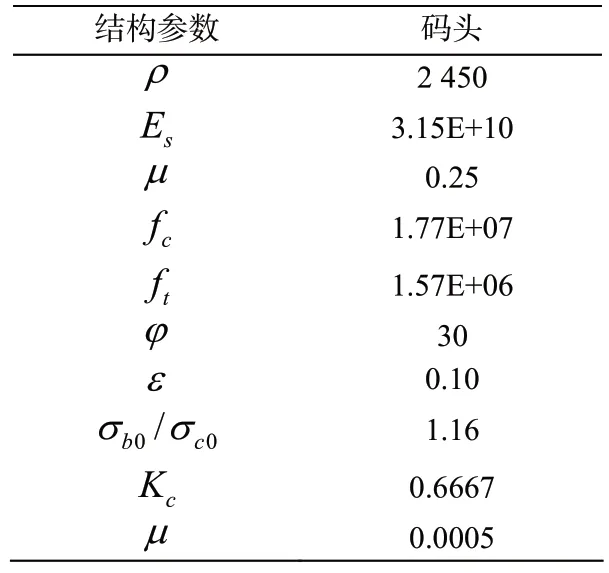
表3 码头模型材料参数

表3 中：φ为剪胀角；ε为流动势偏移量；为双轴受压与单轴受压极限强度比；KC为不变量应力比；μ为粘滞系数。

本文将船舶停靠码头过程中船舶与码头的接触设置为面面接触，选取罚函数算法进行碰撞模拟计算，设置船舶码头之间的面面接触切向摩擦系数为0.2，法向采用硬接触[4]。

本模型模拟一定的水位条件下船舶停靠码头的过程，忽略船舶在水深方向位移，在船舶底面进行边界条件约束，限制船舶在水深方向上的运动。在船舶碰撞码头的过程中，简化了码头底部桩-土结构非线性变化关系。本模型对码头靠船墩承台面以下的桩进行刚性固定。由于码头具有对称性，在对称面上进行对称约束建立原码头的1/2 进行模拟，可以极大地减少分析的计算时间。

首先进行地应力平衡，船舶和浮箱的重力与受到的浮力相平衡，整个模型能量只有船舶的初始动能。对船舶受泊位水流力的影响，本文根据规范[5]将水流力简化为船舶的附加质量1.05 m（m 为船舶满载质量）。

3 船舶直接停靠码头数值仿真

为了得到船舶停靠码头产生的撞击力，本节设置了具体的计算工况，见表4 所示。

表4 船舶撞击码头工况表

3.1 船舶撞击能量转化结果分析

各工况下计算得出能量转化时程曲线，部分图形如图3。

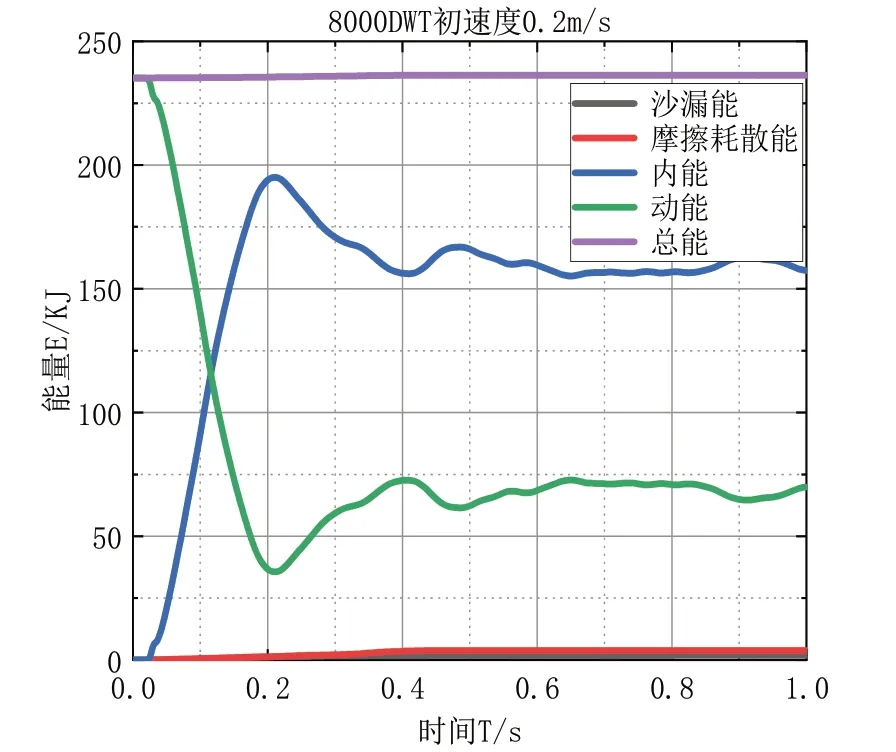
图3 能量转化时程曲线

结合图形分析可知：当3 000 DWT 船舶速度分别为0.2 m/s、0.5 m/s、1.0 m/s 停靠码头过程，系统总能量守恒。动能最低时刻分别为0.13 s、0.20 s、0.37 s，系统剩余动能分别占系统总能量的56.49 %、84.89 %、93.45 %，之后部分弹性变形恢复，能量维持稳定。

5 000 DWT 船舶速度分别为0.2 m/s、0.5 m/s、1.0 m/s 停靠码头过程，系统总能量守恒。动能最低时刻分别为0.16 s、0.37 s、0.49 s，系统剩余动能分别占系统总能量的84.77 %、87.59 %、95.16 %，之后部分弹性变形恢复，能量维持稳定。

8 000 DWT 船舶速度分别为0.2 m/s、0.5 m/s、1.0 m/s 停靠码头过程，系统总能量守恒。动能最低时刻分别为0.21 s、0.48 s、0.71 s，系统剩余动能分别占系统总能量的82.76 %、91.84 %、96.60 %，之后部分弹性变形恢复，能量维持稳定。

综上：船舶停靠码头过程，系统能量守恒，沙漏能低于系统内能的5 %，满足非线性数值模拟的要求，计算结果可靠。碰撞过程，系统的动能转化为内能，动能损失，内能增加。船舶所损失的动能主要被结构的弹塑性变形、船舶与码头接触部位的结构凹陷、钢材失效等吸收，当船舶以较低的靠泊速度（0.2 m/s）停靠码头时，结构主要发生弹性变形，弹性变形恢复，船舶反弹系统内能进而转化为动能；当船舶以较高速度（0.5 m/s、1.0 m/s）停靠码头时，结构主要发生塑性变形，结构破坏，动能转化为内能。随着船舶吨位与船舶停靠速度的增加，动能转化为内能的时长增加，塑性变形越大，动能损失增加，剩余动能减小。

8 000 DWT 船舶以1.0 m/s 的初速度在0°、5°、10°的角度撞击码头的过程，系统不受外力作用，保持总能量守恒。随着初始撞击角度的增加，能量转化时间增加。

3.2 船舶撞击力结果分析

各工况下，计算得出船舶撞击力时程曲线与撞击力统计，部分图形如图4～6 与表5 所示。

图4 撞击力时程曲线

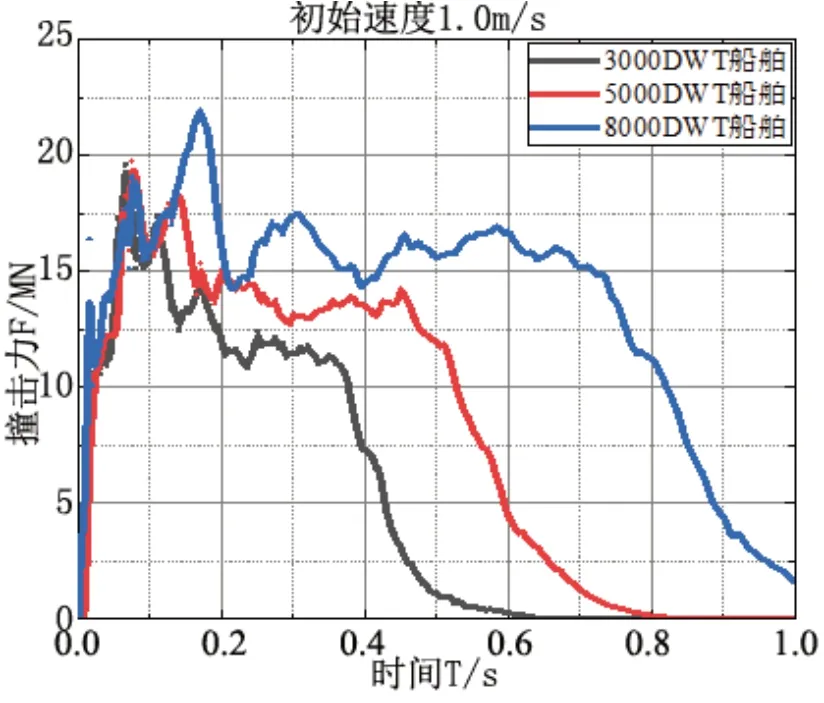
图5 撞击力时程曲线

图6 撞击力时程曲线

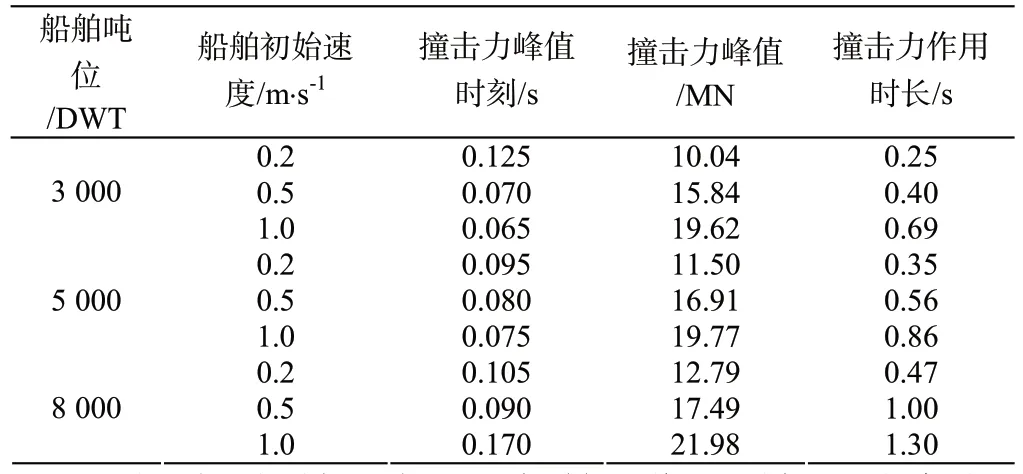
表5 不同工况船舶撞击力统计

1）船舶吨位对码头撞击力的影响

不同吨位船舶撞击力时程曲线走势相似；船舶吨位越大，撞击力出现时间越早，撞击力峰值越大，撞击力作用时间越长；不同船舶吨位引起撞击力差值较小，对撞击力影响较小，撞击力时程曲线波峰较平坦。

2）船舶初始速度对码头撞击力的影响

当3 000 DWT 船舶以0.2 m/s、0.5 m/s、1.0 m/s停靠码头的过程，撞击力最大值分别为10.04 MN、15.84 MN、19.62 MN，出现时间分别为0.13 s、0.07 s、0.065 s，船舶停靠码头撞击力作用时长分别为0.25 s、0.40 s、0.69 s。

当5 000 DWT 船舶以0.2 m/s、0.5 m/s、1.0 m/s停靠码头的过程，撞击力最大值分别为11.50 MN、16.91 MN、19.77 MN，出现时刻分别为0.095 s、0.08 s、0.075 s，船舶停靠码头撞击力作用时长分别为0.35 s、0.56 s、0.86 s。

当8 000 DWT 船舶以0.2 m/s、0.5 m/s、1.0 m/s停靠码头的过程，撞击力最大值分别为12.79 MN、17.49 MN、21.98 MN，出现时刻分别为0.105 s、0.09 s、0.17 s，船舶停靠码头撞击力作用时长分别为0.47 s、1.0 s、大于1.0 s。

综上，不同初始速度、不同吨位船舶停靠码头的撞击力时程曲线走势相似；船舶初始速度越大，撞击力出现时间越早，撞击力峰值越大，撞击力作用时间越长，不同初始速度船舶引起撞击力差值较大，撞击力时程曲线波峰尖锐；船舶吨位越大，撞击力峰值出现时间越早，撞击力峰值越大，撞击力作用时间越长。8 000 DWT 船舶以1.0 m/s 停靠码头的过程，撞击力还未达到峰值时，码头受力破坏，使得撞击力峰值出现时刻较晚。

在同一初始速度下，船舶吨位的增加对撞击力峰值影响较小；在同一船舶吨位下，船舶初始速度增加对撞击力峰值影响较大。

3）船舶撞击角度对码头撞击力的影响

8 000 DWT 船舶以1.0m/s 的初速度在0°、5°、10°的角度撞击码头的过程，撞击力峰值分别为21.98 MN、5.62 MN、5.14 MN，随着初始角度的增加，撞击力峰值减小，撞击力产生时间越晚，峰值出现时间越晚，是因为船舶有角度停靠码头时，船舶绕着接触位置转动，整个停靠过程缓慢，延长了撞击力作用时间。

4 结语

1) 随着船舶吨位与船舶停靠速度的增加，动能转化为内能的时长增加，塑性变形越大，动能损失增加，剩余动能减小。

2) 不同吨位船舶、不同初始速度停靠码头过程系统能量转化曲线、产生撞击力时程曲线走势相似；船舶吨位与船舶初始速度越大，动能转化为内能的能量转化率越高，转化越缓慢，撞击力出现时间越早，撞击力峰值越大，撞击力作用时间越长，撞击力波峰越宽。

3) 当船有角度停靠码头时，停泊角度越大，撞击力峰值越小，撞击力峰值出现时间越晚，撞击力作用时间越长。由于船舶有角度撞击时，部分船舶接触码头，船舶接触码头后绕着接触点转动，接触面积小，撞击力小，能量转换缓慢。

4) 在同一初始速度下，撞击力峰值随船舶吨位的增加缓慢增长；在同一船舶吨位下，撞击力峰值随船舶初始速度增加快速增长，可见船舶初始速度对撞击力影响大于船舶吨级对撞击力的影响。