海域天然气水合物试采目标优选定量评价方法初探

胡高伟，吴能友，李 琦，白辰阳，万义钊，黄 丽，王代刚，李彦龙，陈 强

(1.青岛海洋地质研究所 自然资源部天然气水合物重点实验室，山东 青岛 266071；2.中国地质大学(北京)海洋学院，北京 100083；3.中国石油大学(北京)非常规油气科学技术研究院，北京 102249)

0 引 言

天然气水合物广泛分布于世界主动大陆边缘和被动大陆边缘[1]，因具有巨大的资源量而成为潜在的替代能源。开采方法在一定条件下会影响天然气水合物实际可采量[2-3]，但影响是建立在储量基础之上的[4]。天然气水合物资源的开采还是一个难点，目前仍然停留于探索性试采和试验性试采阶段。尽管西西伯利亚永久冻土带麦索亚哈气田早在1969年就采用降压法和化学抑制剂法成功开采水合物，但其并非专门的水合物开采[5]。就天然气水合物开采方法而言，野外试采结果表明，目前技术上最有效的为降压法开采[6-7]。加热法、注化学剂法、CO2置换法等其他方法，作为辅助开采方法时，虽然在一定程度上能够提高产气潜力，但提高幅度有限。

1 全球水合物试采概况

截至目前全球已实施的多次天然气水合物实地试采(表1)，从2002年在加拿大麦肯齐三角洲多年冻土区砂砾储层为目标进行的5天注热法开采，到2020年我国第二次在南海海域首次利用水平井在黏土质粉砂中进行水合物试验性试采，均显示目前全球已实施的海域水合物试采仍采用降压法。事实上，储藏地质观点认为，影响天然气水合物开采的最根本因素是其实际赋存特征和地质条件，不同的储层赋存条件与规模对开采产气影响巨大。钻探研究发现，不同区域、甚至同一区域不同站位的天然气水合物赋存产出特征差异巨大，这势必会对天然气水合物开采潜能造成影响[8]。

表1 国内外水合物试采概况[6-7]

为了更好地指导天然气水合物勘探与开发，Boswell和Collett(2006)[9]率先提出了“天然气水合物资源金字塔”模型(Gas Hydrates Resource Pyramid,图1)，定性阐述了各种类型天然气水合物储层的资源潜力和开采难度之间的相关关系，为天然气水合物试采指明了方向。从金字塔顶端到底端，各类储层的资源潜力逐渐增大，但资源品位逐渐降低，资源预测可信度相应降低，开采难度相应提高，可采效率逐渐降低。在整个天然气水合物资源金字塔中，极地永久冻土带砂砾质天然气水合物储层属于陆上资源，开采难度最低，开采效率高。对于海域天然气水合物资源而言，开采难易程度由低到高分别为砂质储层、渗透性黏土质储层(含构造、裂隙充填型天然气水合物)、冷泉相关的块状储层以及非渗透性黏土质储层(图1)[10-11]。

天然气水合物资源金字塔仅给出了开采难易程度的定性描述，尚缺少定量数据支撑;并且从中国南海神狐海域的水合物开采经验来看，泥质粉砂水合物储层因具有较好的支撑作用，在合理降压幅度和防砂措施下可以实现较长周期的高产量试采[12-13]；而且，对于同一类型储层，简单利用天然气水合物资源金字塔无法明确最优的开采站位，亟须更为细致、科学的天然气水合物储层产能潜力评价系统，才能更好地为生产开发服务。

目前针对天然气水合物开采目标的选择采取的方法是通过数值模拟的手段,分析得到不同因素影响下的开采产能和工程地质的风险，综合考虑各因素影响确定开采目标。吴能友等[11]2013年提出了水合物开采潜力综合评价方法，该方法利用数值模拟和正交设计建立典型地质参数与开采产气指标的函数关系式，利用函数关系式可以快速对特定储层条件和特定开采方法下的水合物开采产能进行快速的评价。近年来，机器学习和非线性规划方法也应用到了水合物开采目标的优选中。该方法利用机器学习的方法建立数值模拟模型的替代模型，通过替代模型快速计算得到大量的输入输出数据，再利用线性规划的优化方法确定最优解[14]。

利用正交设计建立响应函数的方法可以快速确定不同地质参数对开采产能的影响和最佳地质参数组合，但是响应函数的确定依赖于大量的数值模拟结果的计算，在影响因素众多的情况下，响应函数形式复杂。而机器学习的方法则需要利用替代模型产生大量的数据进行训练，在影响因素众多的情况下，替代模型的构建和检验较为困难。因此，本文基于模糊综合评价理论，建立水合物试采目标的综合评价指标体系，使用数值模拟和实验模拟等定量化手段，计算获得了模糊综合评价中的工程因素和地质因素的权重以及对试采目标影响程度的量化指标，解决了依靠专家经验计算权重时易受人为主观判断影响的问题，实现了试采目标优选从定性到定量的转变。

2 试采目标优选定量方法的建立

2.1 模糊综合评判原理

模糊综合评判是模糊系统分析的基本分析方法之一，在科学评判、项目评审、预测与决策等方面有着广泛的应用，主要用于问题的评价和决策[15]。

所谓综合评判[16]，就是通过对多个相关因素的综合研究，对某一对象进行恰当地评判。一个事物往往需要多个指标刻画其本质与特征，并且人们对一个事物的评价又往往不是简单的好与坏，而是采用模糊语言分为不同程度的评语。对此可采用模糊评判模型加以表达。

在模糊系统分析中，有两种综合评判模型，分别是主因素突出型和加权平均型。在海洋天然气水合物试采最优目标的研究中，选用加权平均型综合评判模型进行评判预测更为合适。基本的模糊综合评判步骤如下：

(1)建立因素集。

因素集是以影响评判对象的各种因素为指标所组成的一个集合。对于海洋天然气水合物试采最优目标的研究，假定从n个方面(因素)来刻画，因素集U可定义为：

U={u1,u2,…,un}

(1)

其中：ui表示各影响因素。

(2)建立权重集。

一般来说，各个影响因素ui对所研究问题的影响程度是不同的，因此，对各影响因素要赋予相应的权重数来表征，各因素权重的分配是因素集上的一个模糊子集A：

A={a1,a2,…,an}

(2)

实际应用中，常要求ai满足归一化条件和非负性条件，即：

∑ai=1，ai≥0，i=1,2,…,n

(3)

权重集A值是在考虑各指标所具有物理意义的重要性顺序后，根据各个指标对于评价影响的重要程度，利用层次分析法求得的，它是用一定的标度把人的主观判断进行客观定量化。

(3)建立评语集。

假设所有可能出现的评语有m个，例如大、较大、中、较小、小等，那么评语集V可表示为：

V={v1,v2,…,vm}

(4)

(4)建立评价集。

在综合评判过程中，评价集是待定的。由以下过程求得：

首先要进行单因素的评价。例如对因素集中的某一个因素ui，那么对其单因素评判结果为V上的模糊子集：

Ri={ri1,ri2,…,rim}，i=1,2,…,n

(5)

式中：Ri为对ui的单因素评价，根据样品参数划分区间上的隶属度来表征。隶属度的确定是在对模拟结果统计的基础上，赋予各参数的隶属度值。

多个单因素评价综合起来构成单因素评判矩阵R：

(6)

然后就可以根据权重集A和评判对象的单因素评判矩阵R，得到对该评判对象的综合评判结果，为m指标的评价集：

B=A·R

(7)

采用加权平均型的综合评判模型，将式(7)展开为加权求和的形式，即得评价结果bj：

(8)

2.2 指标权重计算

指标权重计算是根据层次分析法[17]计算权值步骤计算各因素权值。所谓层次分析法，是指将一个复杂的多目标决策问题作为一个系统，将目标分解为多个目标或准则，进而分解为多指标(或准则、约束)的若干层次，通过定性指标模糊量化方法计算出层次单排序(权数)和总排序，以作为目标(多指标)、多方案优化决策的系统方法。层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的目标顺序分解为不同的层次结构，然后用求解判断矩阵特征向量的办法，求得每一层次的各指标对上一层次某指标的优先权重，最后再用加权求和的方法递归求得各备选方案对总目标的最终权重，此最终权重最大者即为最优方案。这里所谓“优先权重”是一种相对的量度，它表明各备选方案在某一特点的评价准则或子目标下优越程度的相对量度，以及各子目标对上一层目标而言重要程度的相对量度。层次分析法比较适合于具有分层交错评价指标的目标系统，而且目标值又难于定量描述的决策问题。其用法是构造判断矩阵，求出其最大特征值及其所对应的特征向量W，归一化后即为某一层次指标对于上一层次某相关指标的相对重要性权值。

(1)指标权重的计算步骤。

步骤1：建立层次结构模型。在深入分析实际问题的基础上，将有关的各个因素按照不同属性自上而下地分解成若干层次，同一层的诸因素从属于上一层的因素或对上层因素有影响，同时又支配下一层的因素或受到下层因素的作用。最上层为目标层，通常只有1个因素，最下层通常为方案或对象层，中间可以有一个或几个层次，通常为准则或指标层。当准则过多时(譬如多于9个)应进一步分解出子准则层。

步骤2：构造成对比较阵。从层次结构模型的第2层开始，对于从属于(或影响)上一层每个因素的同一层诸因素，用成对比较法和1—9赋值比较尺度构造成对比较阵，直到最下层。

步骤3：计算权向量并做一致性检验。对于每一个成对比较阵计算最大特征值及对应特征向量，利用一致性指标、随机一致性指标和一致性比率做一致性检验。若检验通过，特征向量(归一化后)即为权向量；若不通过，需重新构造成对比较阵。

为了使判断定量化，一般引用Saaty[18]提出的1—9标度法求取的。1—9标度法是根据一些客观事实和一定的科学依据而得到的，其含义如表2所示。通过两两比较各要素相对于其上一层次某要素的重要程度，依据1—9标度法(表2)，即可形成判断矩阵P。

表2 1—9标度法赋值含义[18]

(9)

式中:Cij指第i个因素与第j个因素相比的标度值。其判断矩阵满足：

(10)

通过求解判断矩阵的最大特征值及对应的特征向量，确定各层因素权重及组合权重，并对各判断矩阵进行一致性检验。

最大特征向量及特征值的具体计算步骤如下：

步骤一，令判断矩阵P=(pij)n×n，判断矩阵每一行元素的乘积Mi为：

(11)

步骤四，计算判断矩阵的最大特征值λmax：

(12)

式中：(pw)i表示pw的第i个元素。

判断矩阵一致性检验步骤：

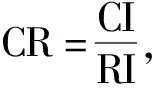
步骤三，当n=1,2时，RI=0，1，2阶的正反矩阵总是一致矩阵，无须判断(表3)。

表3 判断矩阵平均随机一致性指标RI的取值

(2)各因素组合权重计算步骤。

步骤一，计算各因素层判断矩阵特征向量w=[w1,w2,…,wn]T，即该层各因素相对与上一层次的权重值。

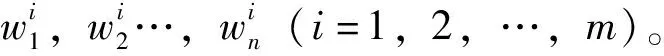
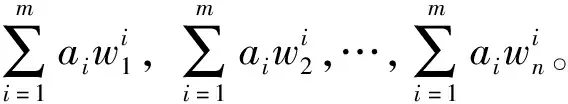
2.3 基于模糊综合评判的试采目标优选方法

考虑影响海洋天然气水合物试采目标优选的主要影响因素[19]，利用模糊综合评判对试采目标区进行综合评价。

首先开展因素集和评语集的建立。水合物试采目标综合评价的因素主要从工程因素和地质因素两个方面考虑(图2)，工程方面考虑的因素主要有水深、强度参数、海底坡度、上覆层厚度等基于工程地质调查的参数[20]。地质因素主要考虑渗透率、孔隙度、水合物饱和度、水合物层厚度、水合物层初始压力和温度6个因素[21]。根据模糊综合评价的原理建立如图2所示的指标体系：

上述指标体系分为两个层次，主层次的因素为工程因素和地质因素两个因素，工程因素下的子层次有水深、海底坡度、强度和上覆层厚度4个因素；地质因素下的子层次有渗透率、孔隙度、水合物饱和度、水合物储层厚度、储层温度、储层压力6个因素。目标综合评价的过程是分别单独评价工程因素和地质因素这两个主层次下各因素的权重，再将主层次两个因素进行权重计算，合并计算子层次的最终权重，然后与单因素评价矩阵计算得到最终的综合评价因子。

地质因素的评价标准有绝对标准和相对标准两种，其中绝对标准包括水合物试采阶段的水合物分解速率、产气速率、水合物累积分解气量、累积产气量、累积产水量等；相对标准仅有一个，即水气比，其物理意义是每单位产气体积下的产水量大小[22]。研究过程中，选取累积产气量和水气比作为衡量水合物试采目标站位优先推荐次序的关键评价标准，对于试采目标站位，累积产气量越高，优先级越高；水气比越低，即产水耗费及处理成本越低，经济效益越好，越适宜优先进行海洋天然气水合物的试采实施[21]。

作为水合物研究使用较为广泛的TOUGH+HYDRATE模拟器，其由美国劳伦斯伯克利实验室开发，其经过马里克实地水合物试采结果的校正，其对水合物产能模拟表现出较高的可信度。前期使用Tough+Hydrate数值模拟结果表明，这6个地质因素对绝对标准和相对标准的影响次序有显著差异。对于累积产气量这一绝对标准，各储层地质因素的影响次序依次为：渗透率、孔隙度、水合物饱和度、初始温度、初始压力、水合物层厚度；对于水气比这一相对标准，各储层地质因素的影响次序依次为：初始压力、渗透率、孔隙度、水合物饱和度、水合物层厚度、初始温度[21]。气水比作为相对标准进行评价时包含了经济效益的因素，而现阶段水合物的试采主要以最大化累积产气量为目标，对于经济效益的评价还需要考虑其他多种因素进行综合评价，故本文以累积产气量作为评价标准。

为综合评价水合物试采目标区的优先推荐次序，建立各主要地质影响因素评判的因素集合U：

U={U1,U2,U3,U4,U5,U6}

(11)

其中：U1表示绝对渗透率；U2表示孔隙度；U3表示水合物饱和度；U4表示水合物储层厚度；U5表示水合物储层初始压力；U6表示水合物储层初始温度。

结合矿场实际，将海洋天然气水合物藏地质因素评价结果细分为三大类，即好、中等、差，建立模糊综合评判的评语集V：

V={好，中等，差}

(12)

水合物试采的工程因素主要影响施工过程，考虑的主要因素有水深、强度参数、海底坡度、上覆层厚度4个因素；建立工程因素这一子层的评价模型的因素集U′：

(13)

结合施工难易程度，将水合物藏从工程角度分为三大类：好、中、差，建立工程因素层的模糊评价评语集V′：

V′={好，中等，差}

(14)

基于上述方法，开发了水合物试采目标综合评价系统PTES[23-24]。

3 参数的确定

根据正交设计统计方法的设计原理，依次为6个地质因素选取不同的水平特征值，如表 4所示。

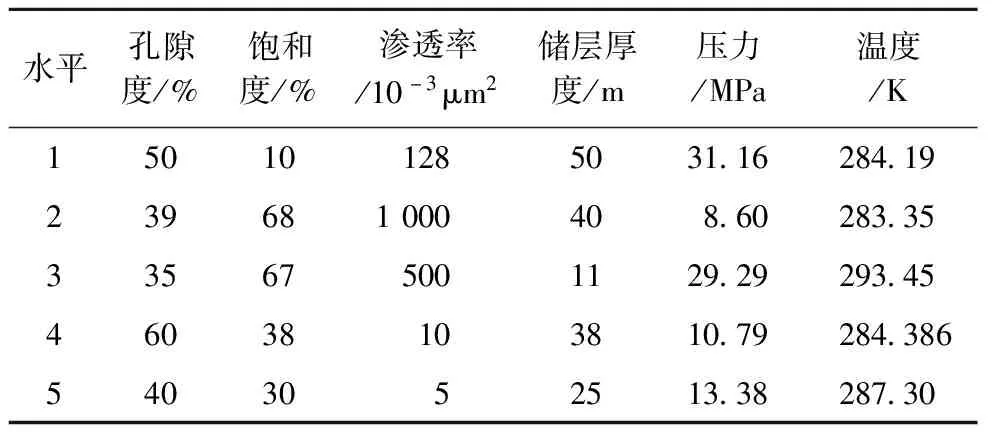
表4 基于全球典型海域水合物赋存特征基础之上的各地质特征水平取值[21]

对以上6因素5水平的因素组合，根据正交设计表必须安排25个方案。值得注意的是，由于天然气水合物藏只稳定存在于一定范围内的温压条件，所以并不是所有构建的因素组合都合理有效[25]。假设所有Class II型甲烷水合物藏内，利用Sloan等在2007年提出的水合物相平衡HYDOFF软件判断在给定温度(或压力)条件下海域水合物藏稳定赋存最低压力(或最高温度)条件[25]。当正交设计中压力(或温度)低于最低压力(或高于最高赋存温度)时，水合物藏处于非稳态，在自然界条件下无法稳定存在。在所有水合物藏模型中，海水盐度取0.03。由HYDOFF计算得到以下7组温度与压力组合时水合物藏处于非稳态：(10.79 MPa，287.3 K)，(8.6 MPa，293.45 K)，(8.6 MPa，284.386 K)，(13.38 MPa, 293.45 K)，(8.6 MPa, 287.3 K)，(10.79 MPa，293.45 K)以及(8.6 MPa, 284.19 K)。因此，最终得到18组稳定条件的水合物藏组合形式，如表5所示。

表5 正交设计中稳定赋存的各地质因素参数组合[21]

考虑每个地质参数的具体取值范围，结合各单因素的评判结果，将其进一步细分，渗透率(10-3μm2)分别为0～100，100～500，>500；孔隙度分别为0～0.35，0.35～0.5，>0.5；水合物饱和度分别为0～0.3，0.3～0.5，>0.5；水合物层厚度(m)分别为0～20，20～40，>40；初始压力(MPa)分别为0～10，10～20，>20；初始温度(K)分别为273.15～285，285～290，>290。这些取值分类分别对应着地质因素评价集的好、中等、差三大类。

考虑每个工程因素的具体取值范围，结合各单因素的评判结果，将各因素进一步划分，水深(m)分别为0～300，300～500，>500；海底坡度(°)分别为0～3，3～5，>5；储层强度(kPa)分别为>180，60～180，0～60；上覆层厚度(m)分别为>200，100～200，0～100。这些取值分类分别对应着工程因素评价集的好、中等、差三大类。

4 综合评价实例分析

利用数值模拟分析获得的各地质因素在水平井试采条件下对产能的影响程度，以中国南海北部陆坡神狐海域4个典型站位的参数为依据，在考虑地质因素及工程因素的情况下，确定以水平井、降压法试采时的最佳站位。需要说明的是，对于水平井开采来说，水平井的长度和布井位置等因素对产能也有影响，但水平井长度和位置等参数是在确定最佳站位后的更进一步的参数优化设计，不在本文的讨论范围内。

(1)基础参数。

根据在南海北部陆坡神狐海域实施的我国海域天然气水合物钻探航次调查研究，4个典型站位的储层地质因素数据具体如下：

XX01站位平均渗透率为0.22×10-3μm2，平均有效孔隙度为34.5%，平均含水合物饱和度为22.9%，水合物储层厚度为78.36 m，平均压力为15.45 MPa，平均温度为14.73 ℃。工程因素方面水深1 309.95 m，海底坡度4°，土强度180 kPa，上覆层厚度113 m。

XX02站位平均渗透率为0.315×10-3μm2，平均有效孔隙度为33.2%，平均含水合物饱和度为19.4%，水合物储层厚度为43.13 m，平均压力为15.38 MPa，平均温度为14.4 ℃。工程因素方面水深1 249.30 m，海底坡度3.2°，土强度170 kPa，上覆层厚度210 m。

XX03站位平均渗透率为100×10-3μm2，平均有效孔隙度为56.7%，平均含水合物饱和度为30.5%，水合物储层厚度为11.56 m，平均压力为14.5 MPa，平均温度为11.22 ℃。工程因素方面水深1 285.41 m，海底坡度3.8°，土强度160 kPa，上覆层厚度144 m。

XX04站位平均渗透率为5.5×10-3μm2，平均有效孔隙度为30%，平均含水合物饱和度为46.2%，水合物储层厚度为17.59 m，平均压力为14.6 MPa，平均温度为9.7 ℃。工程因素方面水深1 273.80 m，海底坡度1.6°，土强度200 kPa，上覆层厚度135 m。

(2)单因素评价矩阵构建。

数值模拟分析得出的结果表明[21]：水合物藏水平井开采时，孔隙度对累积产气量的影响有一定波动；渗透率与开采累积产气量呈现正相关；水合物饱和度对累积产气量的影响也以波动方式为主，而温度则呈正相关，压力呈现先减小后增大的形式。各因素对开采产量的影响趋势如图3所示。利用影响曲线将各影响因素归一化，计算得到各站位的孔隙度、渗透率、水合物饱和度、储层厚度、储层温度、储层压力的单因素评价矩阵：

从施工情况来看，水深越大，越不利于施工，故水深对开采影响为负相关；海底坡度越小越有利于施工，故海底坡度与开采难易程度负相关；储层强度和上覆层厚度越大都越有利于施工，故储层强度和上覆层厚度与开采难易程度正相关。根据工程参数与开采难易程度的相关关系，以简单的单调线性进行隶属度的计算，得到工程参数的隶属度矩阵：

(3)各因素权重计算。

以上数值模拟结果表明各地质因素对累积产气量的影响程度大小为：渗透率>初始温度>储层厚度>水合物饱和度>初始压力>孔隙度。依据不同因素在上述排序中的距离确定标度值，如渗透率的影响程度最大，而孔隙度的影响程度最小，则渗透率与孔隙度相比，其对产能的影响程度强烈重要，即渗透率与孔隙度相比，其标度值为7。依此类推，根据1—9标度法计算各因素的权重，如表6；从权重计算结果看出，各因素的权重大小排序依次为渗透率0.396 1，初始温度0.247 5，储层厚度0.150 2，饱和度0.104 2，初始压力0.061 3，孔隙度0.040 7，与数值模拟计算的结果吻合。

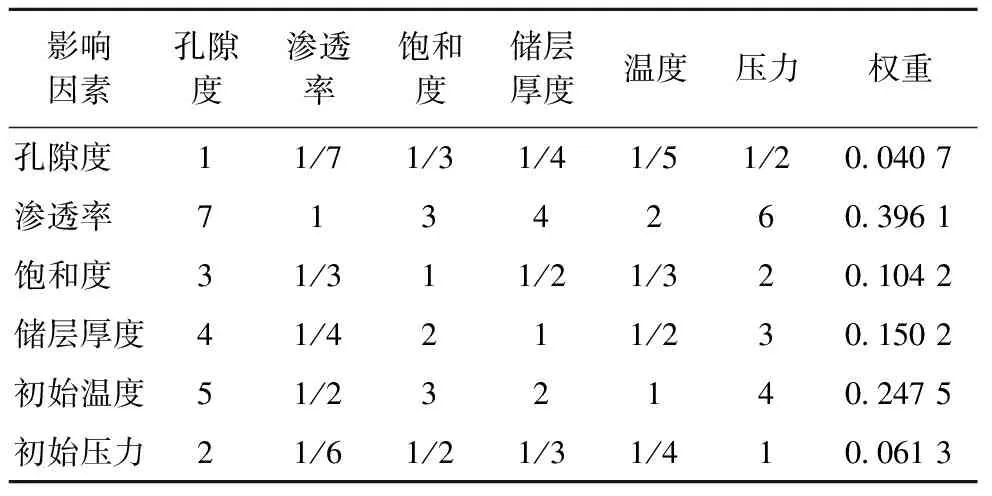
表6 以累积产气量为评价标准下水合物层各地质因素判断矩阵表

对工程因素来说，上覆层厚度直接影响水平井施工过程中造斜是否可行，故其对施工影响程度最高；此外，上覆层强度对施工影响也较为显著，其影响程度次之；海底坡度对施工过程中井口稳定性起关键作用，其影响程度再次之。各工程因素影响程度从大到小分别为上覆层厚度、储层强度、海底坡度和水深。根据1—9标度法，采用与地质因素相同的处理方法，上覆层厚度与水深相比对工程施工影响程度剧烈，故上覆层厚度相对于水深的标度为7，其他因素间根据影响程度的排序取值(表7)。从表7结果可以看出，上覆层厚度的权重最高，且权重值超过0.5，储层强度、海地坡度和水深三个因素的权重值相对于上覆层厚度来说较小，说明上覆层厚度对施工的影响非常大。

表7 工程因素权重计算判断矩阵表

上述过程分别确定了工程因素和地质因素两个主因素的次因素的权重，该权重最终作用到目标层还需要将工程因素和地质因素这两个主因素进行层次分析，获取这两个因素的权重集，如表8所示，假定工程施工因素和地质因素对目标的选择影响程度一样。

表8 工程因素和地质因素两个主权重计算判断矩阵表

最终工程因素和地质因素子因素的权重需要分别乘以主因素的权重获得最终的权重，如表9所示。综合起来看，地质因素中的渗透率权重最高，工程因素中的上覆层厚度权重最高，这与前文的分析一致。工程因素的上覆层厚度的权重值在所有工程因素和地质因素中最高，说明对于水平井开采来说，上覆层厚度能否满足水平井造斜的要求是决定水平井成功开采的前提。

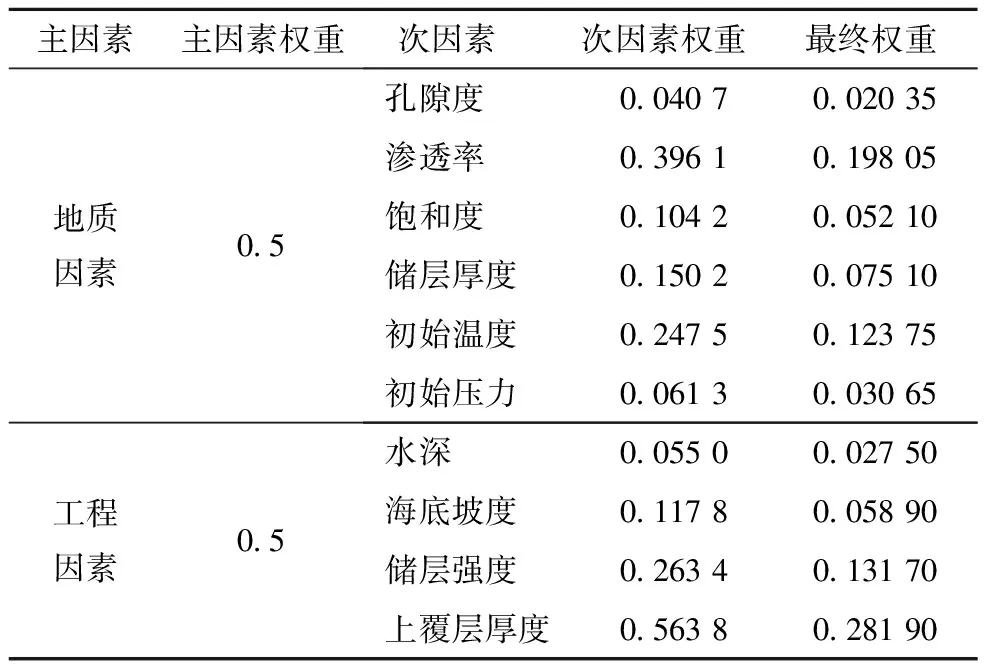
表9 最终权重计算结果

(4)综合评价。

利用权重和单因素评价矩阵计算各站位的综合评价因子，综合考虑地质因素和工程因素条件下得到的评判结果矩阵B=[0.364，0.435，0.353，0.385]。从绝对值上看，4个目标站位所属海洋天然气水合物藏的生产潜力均一般(综合评价因子均小于0.5)。从相对值来看，对于以上4个典型站位，应优先推荐XX02作为水合物试采的目标站位。

5 结 论

综合地质、地球物理、钻探数据等资料，从储层孔隙度、水合物层厚度、水合物饱和度、储层固有渗透率、储层原位温度与压力作为6个主要地质因素出发，联合试采实施的储层水深、海底坡度、强度与上覆层厚度4个工程影响因素，采用模糊数学评价理论和统计分析方法，计算了各影响因素对评价指标的权重关系，建立了水合物试采目标优选的多目标模糊数学的综合评价模型和试采目标综合评价方法。依托该方法，以中国南海神狐海域4个典型站位水合物产出特征为对象，利用评价方法进行了分析讨论，结果显示4个典型站位均不具备有利的产气潜力，但相比较而言，XX02站位因其综合评价因子最高，可以作为试采的优选目标。研究结论与实际数值模拟结果进行了对比，证实了该方法的有效性。多目标模糊数学综合评价方法解决了依靠专家经验计算权重时易受人为主观判断影响的问题，实现了试采目标优选从定性到定量的转变。