平行钢绞线斜拉索索股接触效应与力学行为研究

张卓杰，蒋毅，王熙程，武朝帅，甄晓霞

(1. 石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，河北石家庄，050043；2. 石家庄铁道大学土木工程学院，河北石家庄，050043；3. 道路与铁道工程安全保障省部共建教育部重点实验室(石家庄铁道大学)，河北石家庄，050043；4. 长沙理工大学建筑学院，湖南长沙，410076；5. 华南理工大学土木与交通学院，广东广州，510641)

斜拉桥中常用的斜拉索主要有平行钢绞线索与平行钢丝索。与平行钢丝索相比，平行钢绞线索具有运输方便、易于挂设、防腐性好、更换方便等优点。钢绞线索各部件单独制作、运输，在施工现场逐根张拉，每根钢绞线独立锚固，融拉索和制索为一体，在超大吨位的斜拉索或施工空间受限的斜拉桥中应用尤其广泛。采用平行钢绞线斜拉索是斜拉桥建设发展的明显趋势。平行钢绞线斜拉索由一定数目钢绞线集束而成，钢绞线之间除在某些位置采用刚性索箍紧或者在套管作用下发生耦合外，其他位置独立无黏结，与其他类型缆索结构存在较大差别。因此，平行钢绞线斜拉索实际上是在刚性耦合作用下的多索股系统，平行钢绞线索的振动是各索股相互作用的综合体现，与单根索股或完整性良好的拉索的振动行为均有所不同。

斜拉索的索力和自振频率存在特定关系，可通过测试斜拉索的自振频率获取索力。工程中常采用基于弦理论导出的索力-频率关系式计算索力，此公式简洁方便但不够精确。为了获得更精确的换算关系，学者们进一步考虑索股的刚度、垂度等因素的影响，建立了相应的换算公式[1-5]。这些研究一般假定拉索各组成部件具有良好的完整性，拉索各部件在振动过程中是同步的，而常见的索振动理论均未考虑拉索的内部非完善接触状态，因此，振动频率法测量平行钢绞线斜拉索索力公式的适用性和精确度有待进一步研究。

为了探究振动频率法测定平行钢绞线斜拉索索力的可行性，KANGAS 等[6]基于桥的频谱测试，验证了平行钢绞线斜拉索面内和面外振动的一致性、在不同施工阶段频率的稳定性以及在不同风速下振动频率的变化规律。孙增寿等[7]对已有索理论进行了修正，并通过实测证明了振动频率法对于平行钢绞线斜拉索索力测量的精度基本能满足工程要求。CHO等[8-9]基于实际的斜拉桥，采用多种测量方法测试索力，对比研究振动频率法对于平行钢绞线斜拉索的适用性。平行钢绞线斜拉索本质上是在各类接触效应耦合下的多索股系统，AHMAD等[10-12]对耦合连接的双层及多层索网进行了自振特性分析，提出局部模态化程度和局部模态集群2个指标来评价局部模态的好坏，并对外置阻尼器的混合索网系统的自振特性进行分析；ZHOU等[13-17]对带有阻尼器和交叉连接杆的双层吊索自振特性进行了研究，并提出了新的局部模态化指标，还推导出了考虑拉索垂度在内拉索面内振动方程的解析式。上述研究更侧重于力学特性分析，对在工程实践中的应用论述不多。

为了探明平行钢绞线斜拉索内部的接触来源及其对斜拉索整体力学行为的影响，本文作者根据平行钢绞线斜拉索的构造特点与力学关系，探明索体内部3类接触效应的产生机理；通过理论分析得到索箍刚性耦合下的拉索振动方程及其影响规律；并对外套管和索箍多重耦合作用下的斜拉索自振特性进行有限元仿真分析与试验研究，证明了理论分析的正确性。

1 钢绞线斜拉索的构造特点与接触因素分析

为便于分析，以安徽铜陵公铁两用长江大桥(简称铜陵桥)作为工程背景。该桥采用三榀主桁、三索面布置，主跨为630 m，全长1 290 m。斜拉索采用OVM250平行钢绞线拉索体系，全桥共228根斜拉索，单根斜拉索的钢绞线束数为61～127 根不等。斜拉索编号如图1 所示，首字母S 表示边跨，M 表示中跨，第二个字母S上表示上游侧，M表示中游侧，S下表示下游侧。

图2所示为铜陵桥采用的平行钢绞线斜拉索的典型构造，主要由钢绞线索股、外套管、紧箍装置(索箍)、防水罩、锚具、减振装置等部分组成。索体施工过程中防水罩不下放，可在此处穿入钢绞线；当钢绞线张拉完毕并调整完均匀性后安装索箍，索箍使钢绞线索股排列成规则的正六边形，增强了索体的整体性。

平行钢绞线斜拉索逐根穿束，单根锚固，因此配夹片锚头。图3 所示为典型的OVM 锚板孔位布置(其中，d为层间距)。结合图2 可知，为便于锚固，锚板孔位间留有一定空隙，斜拉索锚板直径大于索体外套管的直径，因而外套管将对外周索股产生几何约束作用。

此外，外套管一般由高聚乙烯(HDPE)制成，材料弹性模量小，且外套管本身并不张拉，较为柔软；内部的钢绞线被施加了较大的张拉力，具有较大的几何刚度，因而外套管的自重将由内部索体承担。在外套管自重的作用下，内部索股可能发生接触。

由此可见，引起平行钢绞线斜拉索内部索股接触的来源主要有3种：索箍的刚性耦合、外套管的几何约束效应、外套管的自重作用；对于采用内置填塞式橡胶圈阻尼的斜拉索，阻尼器也可引起索股发生接触，由于该来源与阻尼器类型有关，本文不考虑此因素。索箍约束作用发生于索箍安装后，作用位置一般位于靠近梁端和塔端索导管出口处；外套管的几何约束作用与套管和锚具的构造、几何尺寸有关；外套管的自重作用则与套管的质量、斜拉索的受力条件有关。

2 索箍耦合效应分析

索箍安装在靠近梁端和塔端索导管出口处，仅在索箍作用下，平行钢绞线斜拉索可以视作图4所示的刚性耦合索股系统。模型由n根独立锚固的等长钢绞线组成，各根钢绞线的长度均为L，索股的拉力分别为T1，T2，…，Tn。钢绞线通过2 个轻质刚性块发生耦合，刚性耦合将斜拉索分为3个子系统，各子系统的长度分别为lj(j为子系统编号)，分别以各子系统的左端为原点建立坐标系xjojyj。

2.1 振动方程

斜拉索为细长结构，不考虑索股抗弯刚度的影响，根据弦理论，单根索股在拉力作用下的横向振动方程为[18]

式中：v(x,t)为索股的横向位移；x为沿索股轴线的坐标；t为时间；T为索股的拉力；m为索股的单位长度质量。

采用分离变量法求解，设方程解的形式为

其中：φ(x)为关于x的函数；q(t)为关于t的函数。

将式(2)代入式(1)，两边同除mφ(x)q(t)，得

式中：ω为圆频率。

对式(3)进行分离变量之后可以转换成以下2个方程：

式(4)和(5)为二阶齐次线性常微分方程，式(4)的解为

其中：

式(5)的解为

因此各子系统内单根索股的振动方程为

式中：i表示索股编号，取值范围为1～n；j表示子系统编号，取值范围为1～3。

根据刚结点处索股振动协调关系，易推知各索股振动同步，即

各索股的区别在于振型方程不同，即

2.2 方程求解

式(9)为含有6n个待定系数的联立方程组，其解可通过边界条件、连续性要求及竖向力平衡条件确定。

1)边界条件

由于索股两端固结，索股端部的位移为0，即

共有2n个方程。

2)连续性要求1

同一索股在耦合处的位移相等，即

共有2n个方程。

3)连续性要求2

同一横向连接相邻索股位移条件为

共有2(n-1)个方程。

4)竖向力平衡条件

索股在耦合处的竖向分力应满足平衡要求，即

共有2个方程。

由上述可得6n个方程，将以上方程写成矩阵形式：

式中：K为6n×6n的系数矩阵；X为6n×1的待定系数列 向 量，

若式(16)有解，则系数矩阵行列式为0，即

式(17)即为频率方程，可借助数学软件MATHEMATICA 求得具体表达式。矩阵K中只有一个未知数ω，求得ω后，根据式(11)和式(16)可求得系数列向量X和各索股的振型。

2.3 频率方程

根据前述方法，对于两索股双刚性耦合索网系统(n=2)的自振频率方程为

随着索股数量增加，频率方程变得非常复杂，通过类推法，可得到双耦合n索股系统的频率方程：

当刚性耦合数量为1时，式(19)可简化为

式(20)为n根索股组成的单刚性耦合索网系统的自由振动频率方程。

2.4 振动试验

为了进一步验证理论的正确性，在实验室进行索股系统振动试验，试验索股采用钢绞线，长度均为3.37 m，截面积为139 mm2，线密度为1.12 kg/m。

钢绞线锚固于反力架上，反力架右侧锚固端安装索力微调螺母，钢绞线左侧锚固端安装穿心压力传感器，可监测钢绞线的张力，钢绞线首先通过千斤顶粗张拉，再通过螺母微调至目标值。在每根钢绞线上分别布置加速度传感器，同步采集各根钢绞线的振动数据。

当2 根索股均被张拉30 kN 时，测量钢绞线在无耦合时和在距两锚固端L/10 处刚性耦合时的振动频率；同时采用ANSYS软件进行仿真分析，钢绞线采用LINK10单元模拟，相关结果见表1。

由表1可知：当索股等张力时，两索股的实测频率基本一致，且无耦合索股高阶频率与基频之间符合整数倍频关系，可证明实测数据的有效性。当索股系统在距两端L/10 位置处耦合后，相较于无耦合情况，在原整数倍频之间出现了分数倍频；本文计算值与ANSYS计算值结果非常接近，与实测值相符度也较好，可证明理论推导的正确性。计算值略小于实测值，其原因主要由于钢绞线存在一定抗弯刚度，使实际振动频率提高。

表1 均匀索力条件下拉索自振频率实测值与计算值Table 1 Measured value and calculated value of selfvibration frequencies under uniform cable forces

进一步调整索力不均匀度为10%，即两索股张力分别为28.5 kN和31.5 kN，对应索股系统的实测频率和计算频率如表2所示。

由表2可见：当系统索股张力不均匀时，索股系统频率实测值与计算值符合度较好，可证明理论推导的正确性。

表2 不均匀索力条件下拉索自振频率实测值与计算值Table 2 Measured value and calculated value of self-vibration frequencies under nonuniform cable forces

2.5 刚性耦合对等张力索股系统自振特性的影响

为了考察局部刚性耦合对索股系统自振特性的影响，分别对等张力条件和不等张力条件下两索股双刚性耦合系统进行参数分析。等张力条件下，假设各索股初始张力均为80 kN，线密度均为1.12 kg/m，索股长L均为120 m。若索股间黏结良好，索股系统可视作完整性良好的柔性弦，根据弦理论可知此时索股的基频fs1为1.11 Hz，且各阶频率与基频成整数倍关系。

为研究刚性耦合对无黏结索股系统振动特性的影响，耦合位置取距索股两端L/10处(耦合①)和索长等分位置(耦合②)。分别使用本文提出的公式和ANSYS计算，二者计算结果相同，如表3所示。其中ANSYS 有限元模型中索股采用LINK10 单元模拟，刚性块位置处的节点进行自由度耦合。

表3 等张力条件下索股系统自振频率Table 3 Self-vibration frequencies under uniform cable forces

由表3 可见：当耦合位置非均匀分布时(耦合①)，系统的高阶频率与基频之比不再保持严格的整数倍关系，相较于完整性良好的拉索，索股系统在整数倍频之间出现分数倍频，如表3 中的1.39 Hz和2.78 Hz等。而当刚性耦合沿索长均匀分布时(耦合②)，索股系统的振动频率均为整数倍频，与完整性良好的拉索振动频率相同。系统各阶频率对应的振型可根据ANSYS有限元仿真分析得到，部分振型如图5所示。

由图5可知：对于耦合索股系统的振型既存在表征整体振动的“整体振型”，也存在表征索股独立振动或局部振动的“局部振型”[19-20]，系统的振型与耦合分布情况有关。当刚性耦合沿索长非平均分布时，整数倍频对应索股的整体振型，分数倍频对应的振型为表征索股独立振动的局部振型。

当刚性耦合沿索长平均分布时，索股系统的振动频率虽然全为整数倍频，但与整体性良好的拉索的振型并不完全相同。例如，双耦合②的3阶频率为3.34 Hz，对应于图5(b)中的4种振型，包含1 种整体振型3 种局部振型。因为仅通过测试频率无法区分它们，所以表3将其归为同一阶。

2.6 刚性耦合对不等张力索股系统自振特性的影响

改变两索股的索力不均匀度至20%，即两索股张力分别为72 kN和88 kN，索力之和保持不变，分别计算单耦合、双耦合索股系统的自振频率；对于每种耦合，耦合情况与2.5节中相同，计算结果如表4所示。

表4 非均匀索力条件下索股系统自振频率Table 4 Self-vibration frequencies under nonuniform cable forces

由表4可见：当各索股索力不等时，索股系统呈现更为复杂的振型与自振频率，系统各阶振型频率不再出现等值的情况(即图5 中的等频振型)，因此，通过频率反推振型成为可能。此时索股各阶振动频率与fs1之比不再保持严格的整数关系，即索股系统的整数倍频消失，但仍存在与fs1之比接近整数倍关系的频率，为保持和前文的对应关系，仍称之为“整数倍频”。这表明虽然索力分布不均匀，但在刚性耦合作用下，系统的整数倍频仍和整体性良好的拉索具有较好的比拟性。

因此，当索股系统的索力不均匀性不过大时(＜20%)，识别出整数倍频后，可仍按照传统的振动频率法测试索股系统总索力。比如对于双耦合②，若以6.73作为6阶频率反算的基频为1.12 Hz，对应整体性良好的单索基频为1.11 Hz，按照弦理论换算的索力相对误差小于2%。

3 外套管自重作用

外套管自重引起钢绞线间的接触原理如图6所示。当无外套管作用时，钢绞线成层状分布，且因为钢绞线等张力，所以各层之间无接触，假设层间距为d。当考虑外套管的作用时，外套管的自重q将首先传递给与之接触的顶层钢绞线，顶层钢绞线将在套管自重作用下发生下挠。若下挠量小于层间距d，则套管自重将仅由首层钢绞线承担，外套管自重并不会引起内部钢绞线接触；当下挠量超过层间距d时，顶层钢绞线将与第二层钢绞线发生接触，护套管的自重将由前两层钢绞线分担，且接触长度与力学条件有关；在外套管的自重作用下，前两层钢绞线将继续下挠，若下挠量小于d，则钢绞线索股停止后续接触，若下挠量超过d，则下层钢绞线将继续发生接触。

根据钢绞线的层状分布特点，以及套管自重往下逐层传递的特性，为了简化分析，假定同层钢绞线的力学行为相同，进一步将平行钢绞线斜拉索等效为图7所示的层状结构。

为了考察套管自重对钢绞线接触的影响，采用ANSYS 进行接触分析。钢绞线依然简化为图7所示的层状结构，各层截面的等效尺寸根据钢绞线截面特性相等的原则确定。为提高计算效率，钢绞线采用LINK10单元模拟，钢绞线各节点采用接触单元COMTA178 连接，单元接触间隙根据钢绞线间的几何关系确定，为19.5 mm，护套管自重采用质量单元MASS21 模拟，均匀分布于顶层钢绞线各节点。

图8 所示为平行钢铰线斜拉索接触模型。图9所示为铜陵桥SM-10 索局部接触状态情况，设索长为L，红色表明接触间隙为0，索股发生接触；蓝色表明接触间隙非零，层间尚未发生接触。

由图9可见：对于SM-10索，索体中央位置处接触层数最多，为10 层，从中央向两端接触层数逐渐减少。铜陵桥其他各索接触情况如表5所示。

由表5可见：外套管自重引起的钢绞线间的接触数量与斜拉索的构造、力学条件有关。随着斜拉索长度增加，外套管质量增加，斜拉索倾斜角减小，垂度效应加强，导致钢绞线的接触数量增加；从6号索开始，内部钢绞线的接触比例已经超过一半；对于长索，内部钢绞线在外套管自重作用下的接触比例已接近或达到100%。

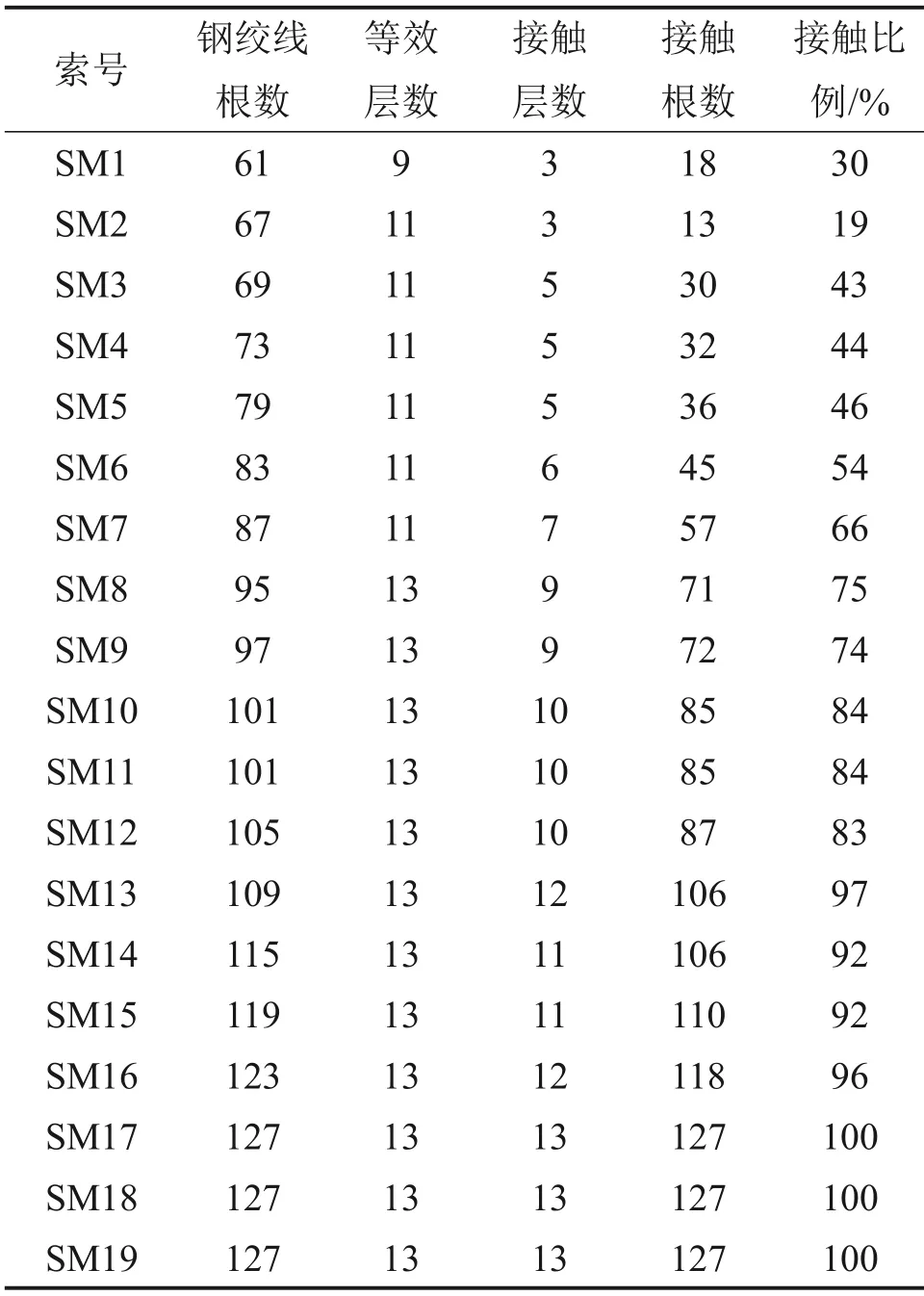
表5 铜陵桥各索在外套管自重作用下的接触情况Table 5 Contact proportion of all cables for Tongling Bridge under self-weight of outer pipe

4 多重耦合下钢绞线斜拉索的振动特性

根据第2节的分析可知，索箍耦合可以保证钢绞线索股振动一致性，且整数倍频与整体性良好的拉索具有比拟性。为了同时考虑索箍、外套管自重的耦合作用对平行钢绞线斜拉索自振特性的影响，取铜陵桥SM-6 索，使用ANSYS 进行自振分析。

为简化分析，平行钢绞线斜拉索仍然取为图7所示的层叠结构，使用LINK10单元模拟。对于外套管自重引起的耦合效应，当斜拉索做微振动时，可认为耦合状态保持与静力状态相同；ANSYS 完成接触分析后得到的耦合关系可继续保留作为模态分析的耦合条件；此外，为考虑索箍的耦合作用，在索箍位置处建立刚性连接耦合相关节点。相关计算结果如表6所示。为作对比，表6中“单根拉索”数据为按钢绞线总面积、总索力相同原则等效的整体性良好的单根拉索的振动频率。

由表6 可见：2 种耦合情况下斜拉索的自振频率与单索自振频率的相对差值小于3%，表明耦合使平行钢绞线斜拉索的振动频率与等效的单根拉索振动频率具有较好的比拟性。表6 中“自重作用”列的数据对应于安装索箍前，仅在外套管自重作用下发生接触部分的钢绞线的自振频率，由于SM6 索仅发生了6 层层间接触，外套管的自重仅由接触部分的钢绞线承担，导致振动频率略有降低；当进一步考虑索箍耦合作用时，表6中“自重作用+索箍”列的数据表明平行钢绞线斜拉索的自振频率与等效单索的自振频率相对差值进一步降低。由此可见，随着耦合因素增多，钢绞线索股的整体性进一步加强。

表6 SM-6号索自振频率计算结果Table 6 Calculated self-vibration frequency of SM-6

5 外套管几何约束

因为锚固直径大于外套管直径，所以外套管对索股将产生几何约束。图10 所示为铜陵桥采用的几种OVM 型锚具和外套管相对几何尺寸关系，图中绿色圆圈代表外套管，红色圆点代表钢绞线束。

根据图10 所示的几何关系可知，处于外套管外侧的钢绞线或者投影图中与外套管有重叠区域的钢绞线，在外套管约束作用下将继续内移，与内层钢绞线发生接触；仅统计图中红色的钢绞线数量，忽略外侧钢绞线内移引起的后续接触，可以得到仅在外套管几何约束作用下的最低接触比例，如表7所示。

由表7可见：由于外套管的几何约束作用可使钢绞线接触比例达40%甚至更多，且该接触效应与斜拉索受力无关，仅与钢绞线索体尺寸有关。

表7 外套管几何约束作用下的接触比例Table 7 Contact proportion of stands under constraint of outer pipe

6 耦合作用下振动一致性实测

根据前述研究可知，各种耦合因素使钢绞线索股振动同步，耦合后的钢绞线斜拉索与等效的单根斜拉索具有比拟性。基于铜陵桥SM-1索，对索股振动一致性进行实测验证。

因平行钢绞线斜拉索在施工过程中防水罩不下放，有部分索体外露，可以在单根钢绞线和外套管上分别绑扎拾振器，采集斜拉索的振动信号进行对比。拾振器的绑扎方位如图11所示。

图12 所示为试验组“索体0°-索体90°”和“套管0°-索体90°”2种工况实测结果，其“索体”表示拾振器的绑扎位置为外露的钢绞线索股，“套管”表示拾振器的绑扎位置为外套管，角度为对应位置处拾振器的方位角。

由图12 可见：对于同一根索，不同位置和方位角的各拾振器的测试频率非常接近，虽然无法测量内部索股钢绞线的振动情况，但至少表明在外套管几何约束和自重作用下，发生接触部分的钢绞线索股振动是同步的。

按照类似的方法继续测量本桥其他的斜拉索，可得到相同的结论。当安装索箍之后，钢绞线索股被全部耦合，振动一致性将进一步加强。这也是振动频率法测试钢绞线斜拉索索力最重要的前提条件。

7 结论

1)对于常规的平行钢绞线斜拉索，索箍使钢绞线索股全部耦合，振动具有一致性；外套管的几何约束和自重效应引起的接触区域与索体的构造、受力条件有关，可进一步提升斜拉索的耦合强度，当考虑外套管的耦合作用时，斜拉索的整体性得到进一步加强。

2)索股系统的自振频率是各索股在耦合下作用下振动的综合体现。相较于整体性良好的拉索，刚性耦合索股系统的自振特性更加复杂，在整数倍频之间出现了分数倍频，在整体振型之间出现局部振型，且振型分布与耦合的位置和数量有关。

3)接触效应保证了耦合索股振动的同步性，使整数倍频与整体性良好的拉索的自振频率具有比拟性。当索股索力分布不均匀时，耦联作用也可显著降低主振频率与整体性良好的拉索对应阶次fsk之间的偏差。当采用振动频率法测试平行钢绞线斜拉索索力时，可通过刚性结构对索股进行紧箍来提高测试精度。