BCl3分子振动频率的同位素效应
杨志杰, 马俊平, 唐 显 , 李 鑫, 李业军, 闫 冰
(1.中国原子能科学研究院同位素所, 北京 102413; 2.吉林大学 原子与分子物理研究所, 长春 130012)
1 引 言
具有相同的质子数,不同的中子数的原子互为同位素. 原子核是由质子和中子构成的. 因此,同位素之间原子核的结构存在差异. 同位素核质量不同,电荷分布不同(中子数不同)会使原子能级发生位移,即同位素位移. 同位素位移是原子分子光谱学的重要内容之一. 研究同位素位移对于了解原子核内部复杂性质和研究分子结构具有重要意义. 例如,同位素位移可用于测量原子的电荷半径[1,2],研究原子分子的能级结构和自旋轨道特征[3,4]. 此外,同位素位移还应用于核动力研究和冷原子物理等领域[5,6]. 硼元素含量约占地壳组成的0.001%,在自然界中主要以硼砂和白硼钙石等矿物形式存在. 硼稳定的同位素有两种,即10B和11B,相对原子质量分别为10.01和11.00,其中10B的天然丰度为19.78%,是慢中子的良好吸收剂,吸收中子时同时发射高能α粒子,可用于中子计数管,在核反应堆里用做防护屏,控制棒,也用于核医学. 硼元素与卤族元素(X)可以形成BX3形式的化合物,其中BCl3用途广泛,可用于制造高纯硼、有机合成用催化剂和超硬材料氮化硼的合成原料等[7].
自上世纪60年代激光出现以后,激光同位素分离(Laser Isotope Separation-LIS)激发人们极大兴趣,先后提出了分子激光同位素分离法(Molecular Laser Isotope Separation-MLIS),原子蒸汽激光同位素分离(Atomic Vapor Laser Isotope Separation-AVLIS),已将实现的第三代铀浓缩技术是激光激发同位素分离法(Separation of Isotopes by Laser Excitation-SILEX),属于分子法的一种. 相较于传统的气体扩散法、离心机法,SILEX具有投资少、规模小、浓缩率高、能耗低、经济性好等优点. SILEX还可用于分离硼、硅、碳等同位素,对于国防、能源、高技术及核医疗发展具有重要影响. 开展BCl3分子的振动模波数ν与同位素频移Δν理论计算研究,可为实验测量分子光谱提供理论指导,也是激光技术路线选择与方案设计的理论依据,为SILEX浓缩硼(BCl3)奠定良好研究基础.
实验方面人们对BCl3的振动结构的研究已有大量的工作. Anderson 等人在1936年使用汞灯的253.7 nm光谱线为激发光源,通过Nicol棱镜进行分光,使用摄谱仪进行曝光获得BF3、BCl3和BBr3的拉曼光谱数据;进而结合理论分析得到了BCl3的v3振动的硼同位素位移为38 cm-1[9]. Maier等人在1980年利用傅里叶变换红外光谱仪得到了固态氩和氪基质隔离条件下的BCl3和BCl2F的高分辨红外吸收光谱数据,并获得了振动频率[10];由于受到Ar和Kr原子的限制,分子的振动频率与单分子状态下的绝对数值上是有差异的,然而其v3振动的硼同位素位移(38.7 cm-1)为与之前的实验值(38 cm-1)十分接近. 值得一提的是,虽然基质隔离条件与SILEX浓缩时BCl3分子所处的环境类似,即均可能与Ar等存在相互作用,其光谱数据值得参考,但由于相对的摩尔数可能不同,惰性元素原子对其影响程度可能不同. 理论计算方面,1974年Jancsó等人根据凝聚体系的同位素效应理论,解释了蒸气压下BCl3同位素效应的实验数据[11]. 但是,对于孤立BCl3分子,同位素位移参数方面的理论研究仍然很有限.
为了计算研究BCl3分子振动频率的同位素效应,本文分别采用密度泛函(DFT)与耦合簇(CC)两种理论方法计算研究10BCl3和11BCl3分子的基态平衡结构参数和简谐振动频率.
2 方法和计算细节
对于BCl3分子,本文采用密度泛函(DFT)与耦合簇(CC)两种理论方法计算BCl3分子基态电子结构. 在DFT计算中,采用B3LYP泛函结合全电子高斯基组6-31G(d, p),即B3LYP/6-31G(d, p),优化分子的几何结构并做相应的简谐振动频率分析. 在耦合簇计算中,采用考虑单、双电子激发的CC方法,即CCSD,结合相关一致基组aug-cc-pVnZ(AVnZ,n=T(3),Q(4)),计算了分子结构与频率,并采用下述外推公示(1)获得了完全基组(complete basis set, CBS)下的结果.
E(n)=ECBS+B/n3(n=3,4)
(1)
为了考虑芯-价壳层电子关联(core-valence electrons correlations, CV)对结构与频率的影响,在MP2//MP2(full)/aug-cc-pCVTZ计算了CV效应的修正. 分子的标量相对论(scalar relativistic, SR)修正在B3LYP/aug-cc-pVQZ理论水平下分别采用零阶与二阶Douglas-Kroll-Hess积分计算获得,其中aug-cc-pVQZ基组采用了非收缩形式.
采用上述两种方案分别计算研究了10BCl3和11BCl3分子,计算中能量收敛标准设定为10-8Hatree,密度泛函计算中采用精细网格(75,302). 本文的电子结构计算均采用Gaussian09程序包[12]完成.
3 结果和讨论
在不考虑同位素的情况下,BCl3分子具有D3h对称性,若考虑同位素,分子具有C2v对称性. BCl3分子的ν1,ν2,ν3和ν4振动模式分别为面外弯曲振动,反对称伸缩振动,对称伸缩振动和面内弯曲振动;其中ν3的红外活性最强,也是我们最关注的. 首先采用CCSD/AVXZ(X=T,Q)分别计算了BCl3分子的B-Cl键长与激光同位素分离中关注ν3模式的谐振频率,并采用公式(1)直接外推了几何结构参数与考虑校正因子的频率,结果见表1所示. 进一步地,计算了芯-价电子关联和标量相对论效应对键长与频率的修正,结果列于表1. 因分子电子基态为单重态,未考虑自旋-轨道耦合对结构与频率的影响. 通过上述计算,并考虑各种物理修正,我们得到了分子B-Cl键长的最佳计算值为1.7348 Å,符合了实验测量值[13]1.73 Å的全部有效数字;对于两种同位素分子(11B35Cl3与10B35Cl3),ν3频率与实验值[10]的误差<10cm-1. 计算得到了ν3频率的B原子导致的同位素位移为38.7 cm-1,与实验的同位素位移985.2-946.7=38.5 cm-1相差不到1 cm-1. 不同基组下的CCSD计算的同位素位移Dν3,数值几乎不变,并与实验值符合很好;各种高阶修正对Dν3影响不足1 cm-1,并且部分抵消. 基于上述结果与分析,可见BCl3分子ν3振动的同位素位移对计算的高阶修正不敏感;这种现象主要原因有二,一是高阶效应对分子的振动影响相对较小,二是两种同位素分子的高阶效应部分抵消. 考虑到耦合簇方法的计算较为昂贵,为了计算各种B与Cl原子的同位素构成的BCl3分子的同位素位移,接下来采用DFT理论研究ν3振动的同位素位移.
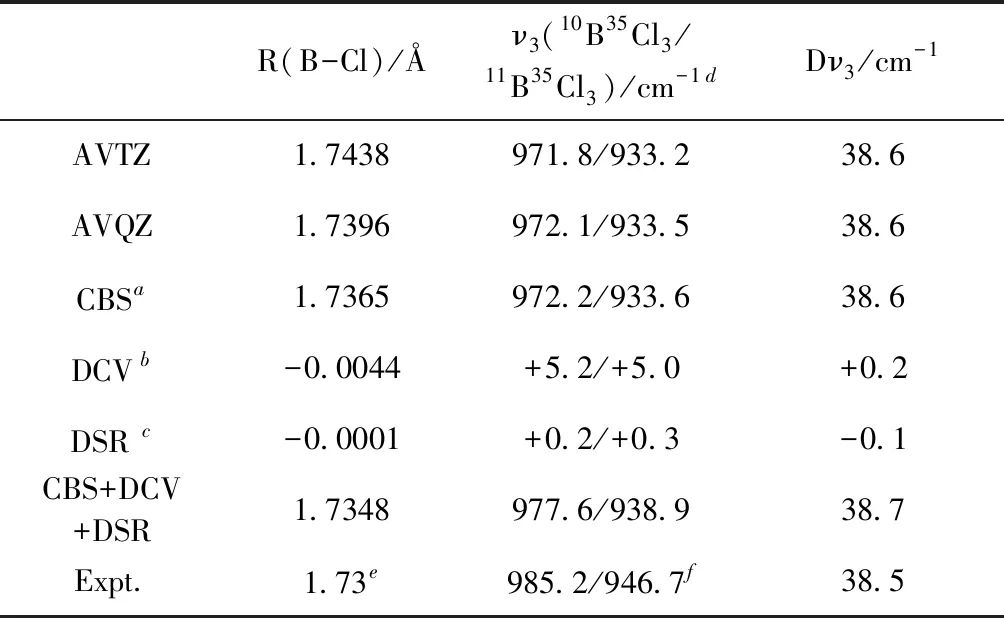
表1 耦合簇理论计算的BCl3的几何结构、谐振频率ν3及其同位素位移
表2中列出了采用B3LYP/6-31G(d, p)计算的两种B同位素(11B35Cl3与10B35Cl3)的B-Cl键长与振动频率,并与实验值[10]做了比较. 对于两种同位素分子(10B35Cl3与11B35Cl3),键长的计算值均是1.7525 Å与实验值1.73 Å的误差为0.0225 Å. ν1和ν2的计算值与实验参考值的误差均<4 cm-1. ν4频率的计算值与实验参考值的误差最大是8.8 cm-1,最小是3.7 cm-1. ν3频率的计算值与实验参考值的误差分别是4.3 cm-1和3.4 cm-1. 计算得到的ν3频率的B原子导致的同位素位移是39.4 cm-1与实验的同位素位移38.5 cm-1相差不到1 cm-1.
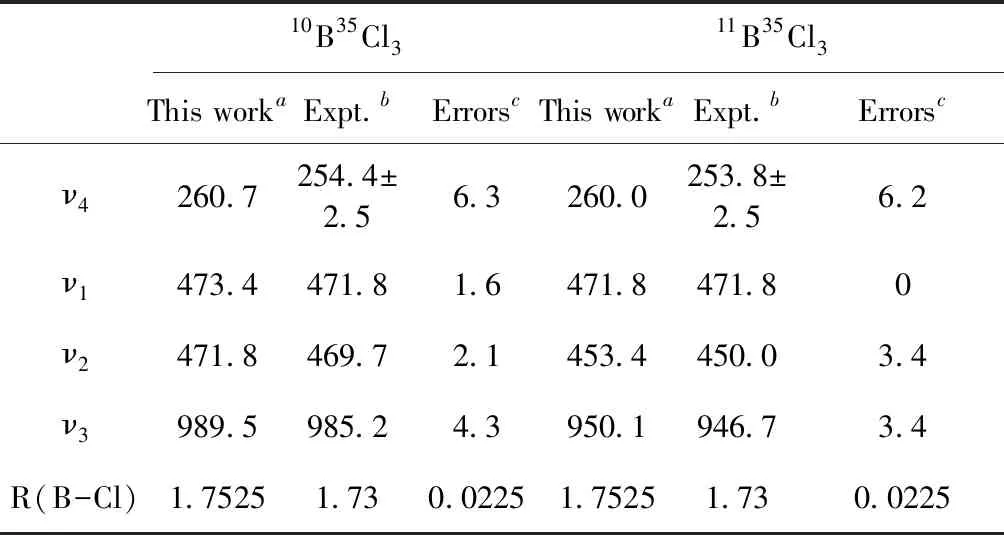
表2 计算的BCl3分子几何结构(键长单位:Å)与振动频率(单位:cm-1)
表3是考虑Cl同位素时,11BCl3与10BCl3的振动光谱分析,从表中可以看出,随着37Cl 比重的增大,ν3振动模式的振动频率会减小. Cl 的同位素自然丰度分别为75.77%(35Cl)和24.23%(37Cl),因为自然丰度是元素的本征属性,且每个BCl3分子含有3个氯原子,我们认为每个氯原子的按照自然丰度分布. BCl3的同位素组成、相对分子质量、天然丰度下各组分的摩尔百分数以及ν3振动光谱(cm-1)列于表3中. 由表中数据可见,同位素组成35Cl35Cl35Cl和35Cl35Cl37Cl的摩尔百分数最大,对于不同的B同位素,随着37Cl 比重的增大,ν3振动模式的振动频率减小. 不同同位素对应不同ν3振动模式的振动频率,可以为采用SILEX方法浓缩BCl3的激光波长选择提供必要的参考.
根据如上分析,11B35Cl35Cl35Cl和11B35Cl35Cl37Cl的摩尔百分数优势明显,且两个分子的振动频率接近,分别为950.1 cm-1和947.6 cm-1,对应的激光激发波长为10.5252 μm 和 10.5530 μm.
4 结 论
采用耦合簇与密度泛函两种理论计算方法,得到了10BCl3和11BCl3分子的基态平衡结构参数和简谐振动频率,并计算了分子ν3振动的同位素位移. 通过将本文给出的数据进行比较,发现计算的振动频率结果与实验值符合较好,考虑到实验是基质隔离条件,二者存在差异也是合理的. 基于对耦合簇方法得到的结果分析,发现BCl3分子ν3振动的同位素位移对计算的高阶修正不敏感;同样,密度泛函方法也确认了这一结论. 两种方法计算得到ν3频率的B原子导致的同位素位移均与实验值相差不到1 cm-1. 这一结论为复杂分子的振动频率的同位素位移的快速计算方案提供了理论支撑,也为激光分离同位素实验的中心波长选择提供了参考.

表3 天然BCl3同位素的组成与ν3振动频率

