具有负泊松比效应的2D碳纳米结构设计及其性能的理论计算研究
袁 焜, 刘艳芝, 吕玲玲
(1. 天水师范学院 化学工程与技术学院理论化学超算中心, 天水 741001; 2. 甘肃高校新型分子材料设计与功能重点实验室, 天水 741001)
1 引 言
最近10多年来,由于在纳米电子器件与光电材料[1-3]、生物材料[4-9]、能量存储[10]和气体分离[11]等领域具有的的重要潜在应用价值,二维碳材料吸引了众多材料科学家的广泛关注和研究. 但是,迄今为止,二维碳材料仍然有很多存在形式值得从理论和实验上研究,特别是从理论上预测能够稳定存在且具有独特力学性质的2D碳材料具有重要科学价值,新型2D碳材料的预测和发现必将对丰富和发展多功能纳米碳材料具有重要贡献.
在通常情况下,2D或3D材料在横向拉伸时,其纵向则表现出收缩应变,即材料会呈正泊松比效应. 但是,也有少数材料在横向(纵向)拉伸时,其纵向(横向)也表现出伸展应变;在横向(纵向)压缩时,其纵向(横向)也表现出收缩应变;这类材料显然具有反常的负泊松比效应. 这样的负泊松比材料在生物医药[12]和保护装备与军工[13]等领域具有巨大的潜在应用价值. 近年来,具有负泊松比效应的单原子层厚度的2D材料已有报道. 在不同的黑磷结构中,材料科学家就发现材料表现出面内及面外负泊松比[14-17]. 此外,在硼烯[18]、柱烷[19]、过渡金属二卤化物[20]和一些尚未制备的材料如五边形石墨烯[21]等材料中,计算材料学家已经预测了其面内负泊松比效应的存在. 最近,Jiang及其合作者[22]从理论上计算研究了单层石墨烯带的负泊松比力学性质,发现这种负泊松比效应是由于边缘压缩应力引起的边缘翘曲的结果. 作者称这种效应非常稳定,在10 nm宽的石墨烯带中,当拉伸应变在0.5%内时,泊松比可以达到-1.51. 此外他们还采用分子动力学方法考察了氧化石墨烯的负泊松比效应,结果表明这种碳材料的泊松比能够通过增大其氧化度来有效调控. 具体来说,“随着氧化程度的增加,泊松比从正到负线性下降,完全氧化石墨烯的泊松比达到-0.567”. 除石墨烯纳米带外,分子动力学计算表明,在应力的作用下,由于去皱作用的产生,波纹石墨烯也呈现出了明显的负泊松比效应[23].
在分子水平上,当材料具有内凹蜂窝状六边形几何结构单元的微结构时,一般会表现出负泊松比效应[24, 25]. 此外,基于内凹六边形蜂窝状的二维经典例子,负泊松比效应最初会很显著,并且会随着六边形凹痕的平展而逐渐衰减[26]. 根据碳原子的成键原理,在分子结构层面,这种内凹六边形蜂窝状结构完全可以通过sp2(苯基或吡啶基)和sp(炔基)碳原子的适当组合设计来实现. 本文利用第一性原理的密度泛函理论计算设计了一种由炔基链、吡啶环及少量氢原子组成的具有内凹六边形结构单元的新型理想二维碳纳米结构,并对其平面内负泊松比效应等力学性能和光学性能与电子结构进行了预测. 我们希望此工作能为在分子层次上具有本征负泊松比的二维碳纳米结构及理论发展提供一种新的设计策略.
2 计算方法
所有计算,包括自洽能量计算和结构优化,均基于投影增强波(PAW)势[27, 28],利用广义梯度近似(GGA)[29]密度泛函理论的Perdew-Burke-Ernzerhof(PBE)交换相关泛函,通过从头算模拟软件包VASP[30, 31]予以实现. 计算中,能量截断设置为500 eV. 2D单层结构在正交单元中建模并驰豫优化,层间的真空层厚度设置超过15 Å,确保层间相互作用可以忽略;采用3×5×1k点网格对结构弛豫过程中的布里渊区进行采样;所有的原子均被完全驰豫,直到它们的原子受力小于0.005 eV Å-1. 自旋轨道耦合对结构变形的影响很小,因此计算中未考虑轨道耦合的影响;对松弛结构进行了振动分析,以确认设计的2D结构的热力学稳定性和晶胞的晶格动力学稳定性.
泊松比根据其定义νbc= -εc/εb计算. 该式中,εb=ΔLb/Lb0是纵向b方向上施加的应变,εc=ΔLc/Lc0是横向c方向上的产生应力. 在计算单轴应变(例如沿b方向)时,人工设定并固定b方向的晶格常数Lb,然后通过优化结构得到对应于所考虑系统最低能量的晶格常数Lc. 最后,可以得到每个应变百分比下的泊松比v.
3 结果与讨论
3.1 结构及其稳定性
在该类结构设计中,我们将吡啶环作为构建单元之一与三炔基相连,同时引入少量必要的氢原子,构筑了2D结构,同样得到了张力得到充分释放、原子间位阻斥力较小的理想二维结构,如下图1所示,该结构单元整体上表现为吡啶环和炔链参与的内凹六边形结构. 为方便讨论,这里将其命名为PACNS. 结构优化结果表明,整个晶胞为完美的正交晶系(晶胞参数如表1所列),且在较宽变形范围内仍然遵循材料力学中的完全弹性理论,具有理想的负泊松比效应(后文将详细讨论). 此外,采用用分子动力学计算探讨了该2D结构的动态稳定性,图2显示了1.3 ps的时间尺度内体系势能变化与时间的关系. 从图中可以看出,最大能量波动约为12 kJ/mol,这意味着该2D结构随着时间的变化其势能波动并不大,且在模拟的时间尺度内,整个2D结构的骨架和几何构型并未有显著的改变. 也就是说,该结构具有较好的分子动力学稳定性.

表1 PACNS结构正交晶胞参数
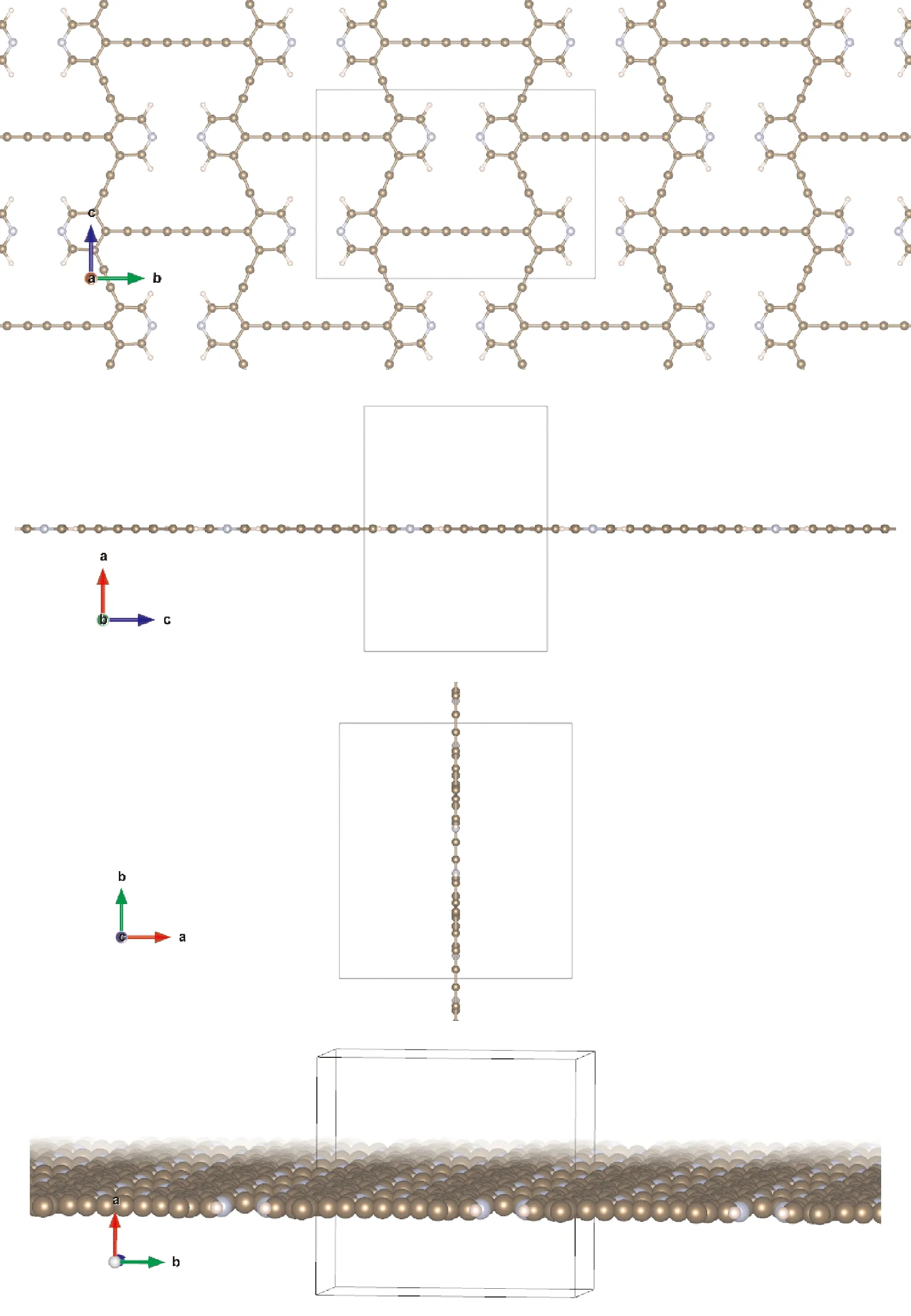
图1 PACNS在a, b, c三个方向上和标准方向上的几何结构Fig. 1 Geometries of PACNS in a, band c directions and standard directions

图2 PACNS结构单元的分子动力学模拟Fig. 2 Molecular dynamics simulation of PACNS structural unit
3.2 负泊松比效应及力学性质
图3(a)为PACNS在c方向拉伸和压缩作用下的泊松比,从图中可以看出,当将该2D结构沿c方向压缩时,其在b方向收缩;当沿c方向拉伸时,其在b方向伸长,即该2D结构同样具有期望的负泊松比效应. 而且,c方向的应变与b方向的应变具有理想的线性相关性. 图3(a)中也显示了c方向的应变在-1%~2%的范围的线性拟合结果,R2=0.983,材料的泊松比为-3.26. 可见,该2D结构在c方向具有显著而稳定的负泊松比效应. 同时,我们注意到沿c方向压缩大于1.1%时,b方向的压缩应变急剧增大,泊松比也随之显著增大,说明PACNS的弹性力学范围相对较窄.
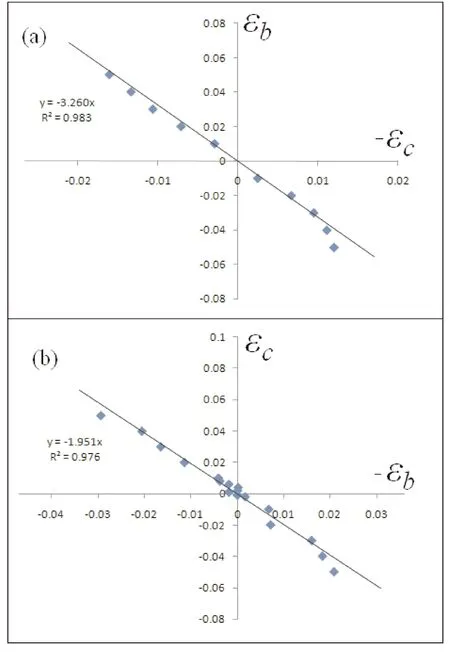
图3 PACNS在c方向拉伸和压缩作用下的泊松比(a)和在b方向拉伸和压缩作用下的泊松比(b)Fig. 3 Poisson’s ratio of PACNS under tension and compression in direction c (a) and that under tension and compression in direction b (b)
PACNS结构在b方向的负泊松比特征与c方向基本相同. 图4-2(b)为PACNS在b方向拉伸和压缩作用下的泊松比. 从图中可以看出,将该结构沿b方向拉伸时,c方向将随之伸长;沿b方向压缩时,c方向将随之缩短. 即无论是沿c方向拉伸还是压缩,该结构都表现出负泊松比效应. 这与b方向的泊松比特征一致, 而且在-2%~3%的范围约为恒定值,但比其在c方向的负泊松比效应弱. 线性拟合的结果显示,沿b方向拉伸或压缩时,泊松比约为-1.951,R2=0.976,可见线性响应特征同样显著,即该方向上材料的弹性力学范围相对较宽. 总之,PACNS结构能够较为理想的实现负泊松比效应的2D碳纳米结构材料.
PACNS结构的弹性常数和其它各种力学模量的计算结果列于表2~表4中. 从PACNS的刚度矩阵(表2)中可以看出,其具有矩阵对角化的数学特征,说明该结构为理想的2D构型,即理想的平面构型,这与前文中几何构型的计算结果完全一致.
从刚度矩阵表2中还可以看出,该矩阵同样虽然并非正定矩阵,但刚度矩阵的6个本征值λ中,只有λ1为绝对值较小的负值,而λ2~λ6均为正值且绝对值依次增大(表3),这说明以这种几何结构的2D材料具有较为理想的机械力学稳定性,而且该材料也具有较好的其它平均力学性能(表4),如较高的体积模量、杨氏模量和剪切模量.
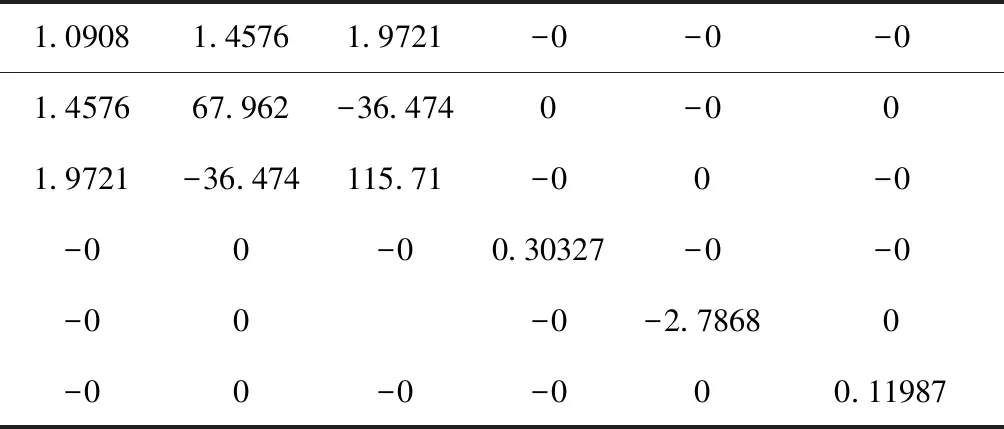
表2 PACNS的刚度矩阵 (GPa)
3.3 光学性质及能带结构
图4~图7分别给出了PACNS的介电函数与电导率、折射光谱、反射光谱和吸收光谱. 从图中可以看出,PACNS结构的光学性质在整体上表现出典型理想2D结构的光学性质和规律. 图4显示,该材料的介电函数的贡献主要来源于其实部. 此外,电导率的实部与电磁波能量之间的变化曲线表明,该结构的电导率在不同的方向上差异较大,特别是当电磁波能量超过3 eV时,与炔基链同向上的电导率达到其最大值. 当电磁辐射能量超过24 eV时,在各个方向上的电导率均收敛于一个较小的正值. 同时,该材料的光学性能也较为优异,如折射系数(图5)和反射率(图6)都较大,而且对电磁波的吸收范围也较宽,特别是在10-20 eV的能量范围内,吸收非常显著(图7). 这可能是由于引入的N原子参与2D网络的形成,除了炔基链上的π电子外,N原子上的孤对电子也可以有效的改善和提升材料的光学性能.
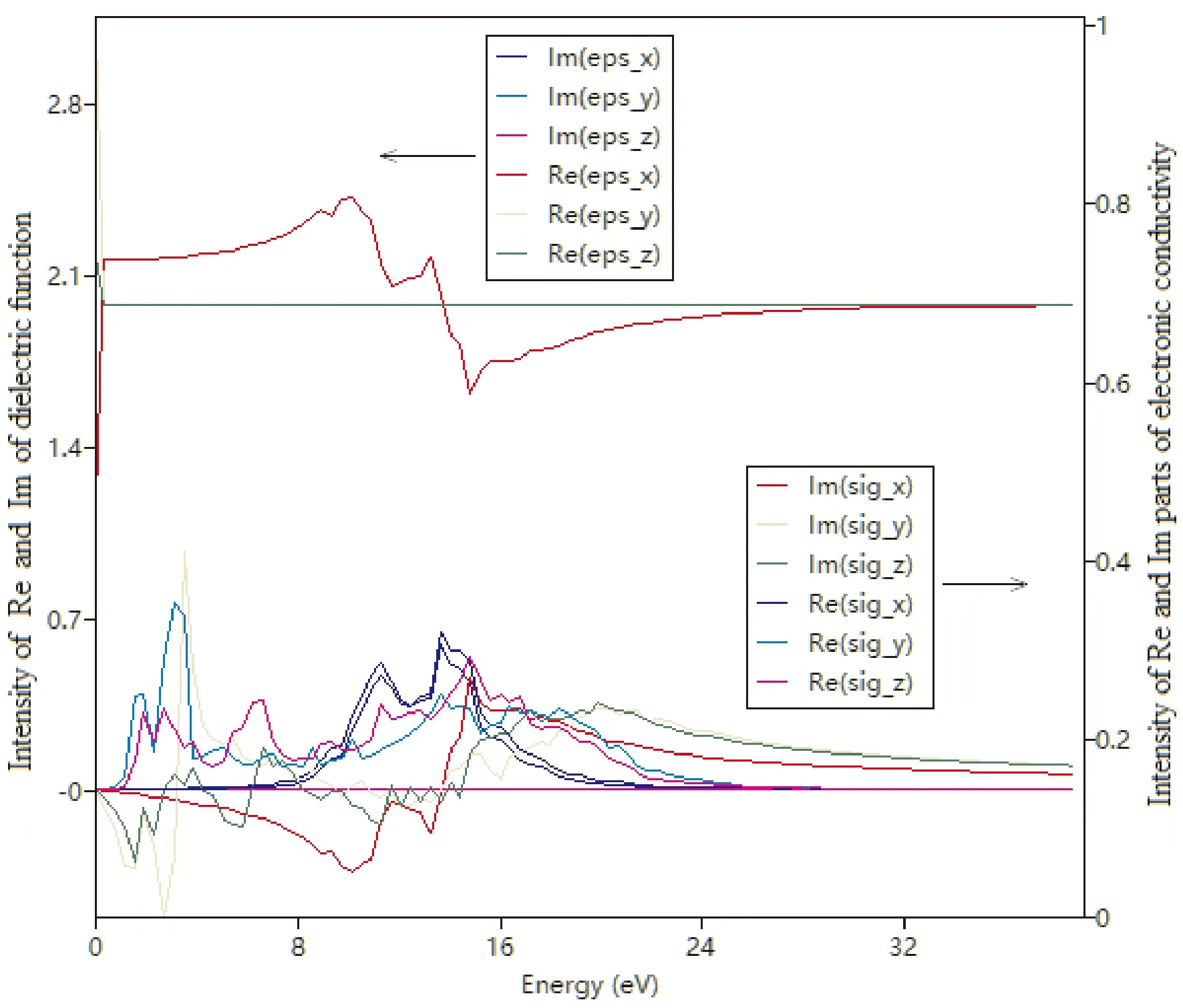
图4 PACNS的介电函数和电导率与电磁波能量的相关性Fig. 4 The relationship between dielectric function and conductivity of PACNS and electromagnetic wave energy
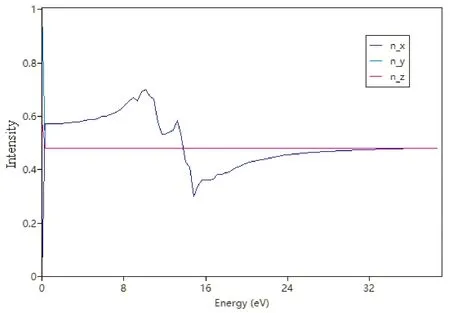
图5 PACNS的折射光谱(折射系数)Fig. 5 Refractive spectrum (refractive index) of PACNS

图6 PACNS的反射光谱(反射率)Fig. 6 Reflection spectrum (reflectivity) of PACNS
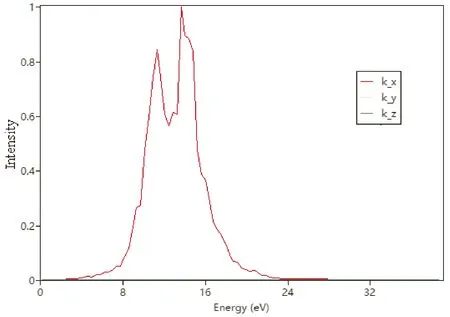
图7 PACNS的吸收光谱(吸收系数)Fig. 7 Absorption spectrum (absorption coefficient) of PACNS
图8给出了PACNS的能带结构和态密度图. 从图中可以看出该2D结构的带隙约为1.0 eV. 可见,与石墨烯和石墨炔的电子结构性质不同,PACNS虽然具有理想的平面构型,但是由于吡啶环及氢原子的引入,使得2D体系中π电子离域程度和范围明显下降,从而表现出半导体材料的电子结构特征.
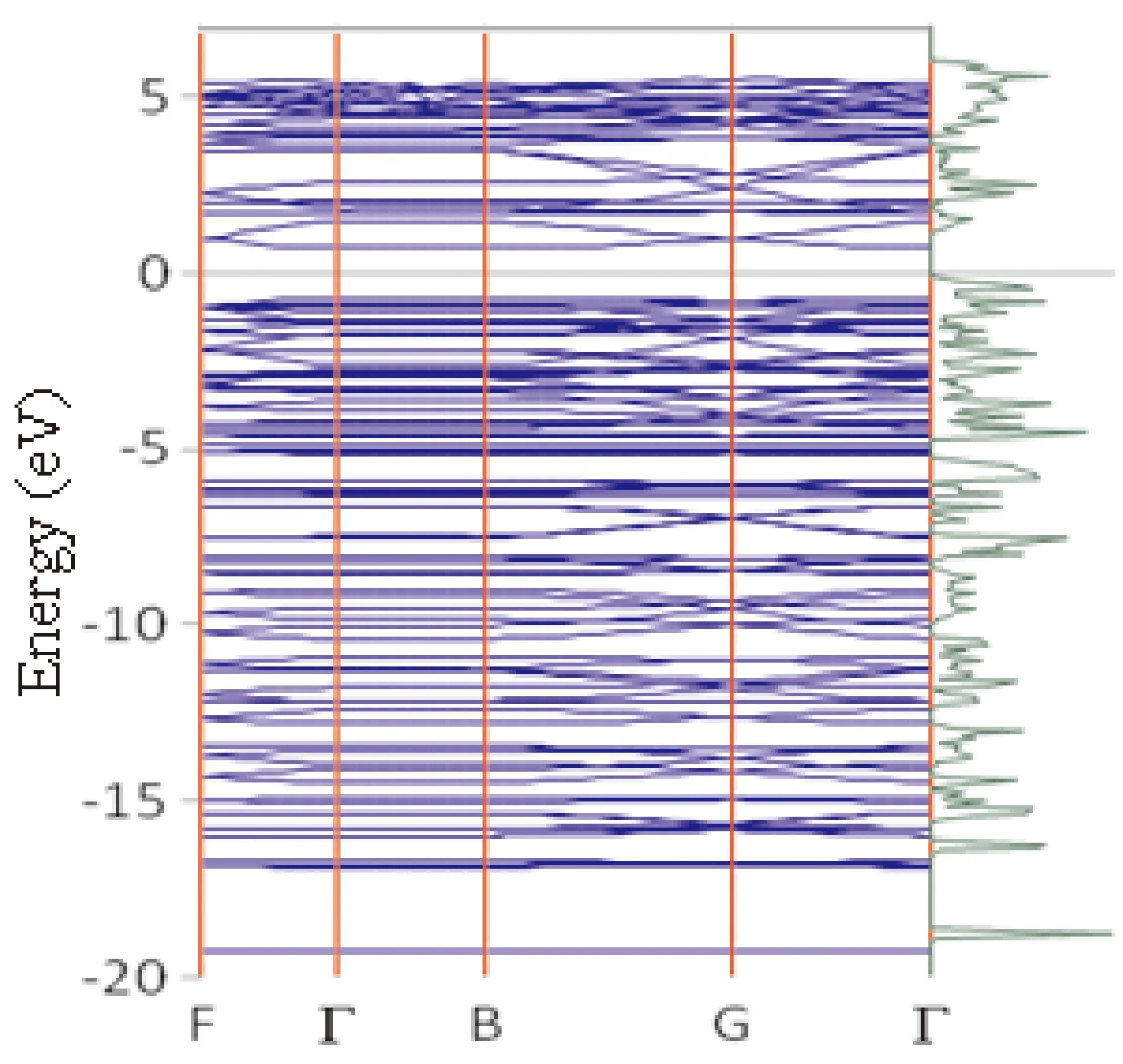
图8 PACNS的能带结构与态密度Fig. 8 Energy band structure and density of states of PACNS
4 结 论
本文采用第一性原理理论计算的方法,设计了一种由C、N和H原子组成的类石墨炔新型理想2D纳米结构材料PACNS. 计算表明,该2D材料具有较好的结构稳定性和特殊的力学性能. 当将该2D结构沿c方向压缩时,其在b方向收缩;当沿c方向拉伸时,其在b方向伸长,即该2D结构同样具有期望的负泊松比效应. 材料的泊松比为-3.26;将该2D结构沿b方向拉伸时,c方向将随之伸长;沿b方向压缩时,c方向将随之缩短. 即无论是沿c方向拉伸还是压缩,该结构都表现出负泊松比效应. 这与b方向的泊松比特征一致, 而且在-2%~3%的范围约为恒定值,但比其在c方向的负泊松比效应弱. 沿b方向拉伸或压缩时,泊松比约为-1.951. 此外,该2D材料表现出半导体材料的电子结构特征和良好的光反射和折射性能.

