不同流动状态下旋转圆柱扰流数值模拟研究

唐卫国 陈 威 吴轶钢 陈 硕 李晓彬

(武汉理工大学船海与能源动力工程学院1) 武汉 430063) (武汉理工大学理学院2) 武汉 430063)(武汉理工大学绿色智能江海直达船舶与邮轮游艇研究中心3) 武汉 430063) (中国船级社武汉分社4) 武汉 430000)

0 引 言

随着海上石油和天然气工业向深水发展,圆柱形海洋结构,如海上风力发电桩腿和石油管道,被广泛应用于海洋工程领域，并对圆柱形结构的扰流及涡激振动进行研究[1-6].不同于常规的固定圆柱形海洋结构物,无立管钻探的钻柱在进行作业时,钻柱壁面的旋转运动会破坏流动的对称性,发生不对称的分离,改变尾涡的释放规律,导致钻柱周围的流场变得更加的复杂.作为钻柱的基础模型,Prandtl[7]的研究表明：旋转能够产生的最大平均升力系数为4π(～12.6),这被称为“普朗特极限”，而且旋转具有一定的抑制涡脱落的作用,利用旋转对流动控制具有重大意义.但对旋转圆柱绕流的研究中还存在一些争议，如普朗特极限能不能被超越,升力系数CL=FL/(1/2)ρU2d、阻力系数CD=FD/(1/2)ρU2d随旋转比α=ϖd/2U的变化趋势，以及斯特劳哈尔数Sr=fvd/U随旋转比的变化规律.

事实上,在不同雷诺数Re=ρUd/μ下,流场和水动力展现的特性会有不同.在低雷诺数下,Chen等[8]观察到,在雷诺数Re=200下,当转速比α=3.25,尾流区有单边涡旋脱落.Mittal等[9]分析了Re=200,0≤α≤5下的二维旋转圆柱绕流,当α≤1.9时发现了漩涡的脱落,同样的发现仅发生单侧涡脱落的第二个不稳定区域(4.34≤α≤4.7)，且在结果中,平均升力系数在α=5时达到了27,远高于普朗特极限值. Stojkovic等[10]在Re=100,4.8≤α≤5.15下发现了第二个不稳定区域,且由于圆柱的旋转,阻力系数均值会出现负值.王丹等[11]对Re=60,80,100,130,160,240下旋转圆柱绕流进行了数值模拟，结果表明：随着旋转速度的增加,临界旋转比增加,第二个不稳定区域前移.Kang等[12]对Re=60,100,160,0≤α≤2.5下的旋转圆柱绕流进行了数值模拟，涡旋脱落在低转速下存在,并在α≥αL时完全消失,其中αL是临界旋转比,它显示出与雷诺数的对数依赖性.在高雷诺数下,Chew等[13]计算了Re=1 000和0≤α≤6时旋转圆柱绕流,并预测α=6时升力系数为9.1,认为普朗特极限不可超越.Karabelas 等[14]也认同普朗特极限值.然而Tokumaru 等[15]使用无粘点涡旋方法研究了在Re=3.8×103处旋转圆柱体周围的流动，发现当α=10时,平均升力系数比普朗特极限大20%以上.Chen等[16]通过试验研究了Re=105下旋转圆柱绕流,发现平均升力系数随转速比的增大先增大,然后保持不变,平均阻力系数最初下降到几乎为零,然后急剧上升,最后保持稳定.孙姣等[17]对Re=1 000下的旋转圆柱绕流进行了实验研究,发现圆柱旋转会改变圆柱的尾流结构,使尾迹尺度变小,在转速比0≤α≤2时,存在明显的周期性漩涡脱落,且脱落频率呈现增高趋势,而当转速比2<α≤5时,尾流场周期性减弱,漩涡脱落不再明显.

以上针对旋转圆柱绕流的研究,仍然存在一些疑问。如升力与尾流之间的对应关系、阻力系数随转速比的变化规律以及不同流动状态下的旋转圆柱绕流的区别等.基于此，文中对层流(Re=200)与湍流(Re=3 900)两种流动状态下的旋转圆柱绕流进行比对分析,阐述了尾涡与水动力之间，以及尾涡结构及水动力参数随转速比的变化规律.

1 计算模型及参数

计算域尺寸见图1。圆柱直径d=0.01 m.计算域长度65d,其中圆柱中心距计算域来流入口15d,距计算域流出口50d；计算域宽度40d,计算域两侧壁面与圆柱中心的距离均为20d.根据文献[18-19],当阻塞率(圆柱直径与流场宽度的比值)小于0.05时,所选取的计算域宽度对结果影响较小,本文选取阻塞率为0.025,满足计算结果不受计算域宽度影响的要求.

图1 计算区域尺寸及网格划分

流体域左侧边界为速度入口(velocity-inlet),方向水平向右，右侧边界为出流(outflow)，上下侧边界设置为滑移边界(moving wall)，滑移速度与入口流速保持一致,由此可模拟无限大流场中的绕流运动.流体介质为水,20 ℃时水的密度为ρ=998.2 kg·m-3,运动黏度为ν=1.004×10-6m2·s-1.

本文研究的主要对象是旋转圆柱在层流(Re=200)与湍流(Re=3 900)流动状态下流场及水动力参数随转速的变化,层流状态下选择数学模型为层流Laminar,湍流状态下选择数学模型为标准k-ε模型.k-ε模型细分为标准、重整化和可实现三种,其中在工程中最常用的是标准k-ε模型.该模型自从被提出之后,就变成工程流场计算中主要的工具.它具有适用范围广、经济、精度合理等优点.其中k-ε模型为双方程模型,是在单方程模型的基础上,引入一个关于湍流动能耗散率ε的方程，即

(1)

湍动黏度定义：

(2)

标准k-ε模型的输运方程为

Gk+Gb-ρε-YM+Sk

(3)

(4)

其中：

(5)

(6)

式中：Gk为由平均速度梯度引起的湍动能产生；Gb为由浮力引起的湍动能产生；T为流场温度；YM为可压缩湍流脉动膨胀对总的耗散率的影响；ρ为流质密度；C1ε、C2ε、Cmu为经验常数,在文中都采用Fluent中默认的值C1ε=1.44、C2ε=1.92、Cmu=0.09；σk、σε分别为湍动能和湍动能耗散率对应的普朗特系数,采用Fluent默认值σk=1.0、σε=1.3；Prt为湍动普朗特系数,Prt=0.85；gi为重力加速度在i方向的分量；β为热膨胀系数；Ma为湍动马赫数；a为声速.

2 模型验证

对Re=200和3 900下的固定圆柱绕流进行数值模拟分析,阻力系数均值CD,mean以及斯特劳哈尔数Sr与其他文献数据对比见表1～2。两种雷诺数下结果相差不大,表明本文建立的固定圆柱扰流模型是有效的.对Re=200下旋转比为1、2.07、3、4四种情况下的旋转圆柱绕流进行了数值模拟分析,升力系数与其他文献结果相差不大，表明本文建立的旋转圆柱绕流数值模型是有效的,即本文所建立的旋转圆柱扰流模型可用来进行下一步的研究.

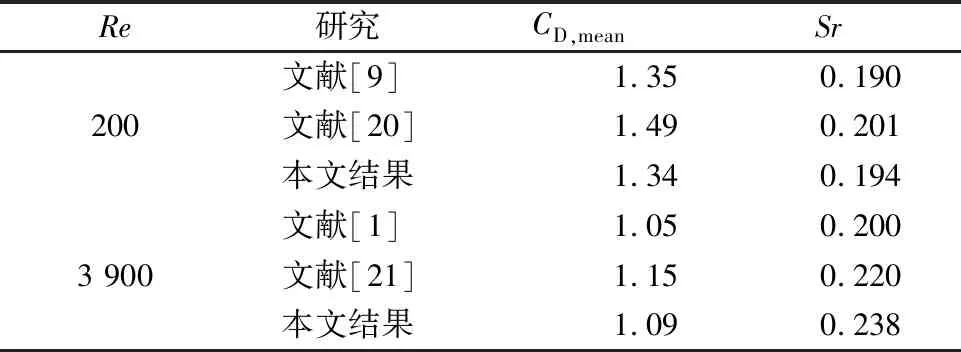
表1 不同雷诺数下圆柱绕流结果比对

表2 Re=200下旋转圆柱的升力系数比较

3 计算结果与分析

3.1 层流结果及分析

图2为Re=200下尾流形态随转速比的变化,存在五种不同的尾涡结构:①漩涡脱落，周期性地从圆柱上脱落两个反向涡流,为2S模式(每个周期有两个单涡脱落),随着转速增大,尾涡被拉长,且尾涡向旋转方向产生倾斜.对应的产生周期性的升力系数；②稳定尾流，漩涡脱落消失,尾流由一正一负两层涡流形成,且负涡位于正涡之上,这种尾涡结构与Bourguet 等[22]所发现的D+结构类似；③反向稳定尾流，与稳定尾流相反,圆柱下部产生的正涡位于负涡之上,与文献[22]所发现的D—结构类似.由于漩涡无脱落情况,对应的升力系数保持稳定；④单边涡，再次出现涡脱落现象,但与2S模式不同,仅在圆柱旋转侧有一个涡脱落,且脱涡频率较2S模式的低,升力系数再次呈现周期性变化,即文献[11]所说的第二不稳定区域；⑤附着涡，由于圆柱的高速旋转,漩涡脱落与稳定尾流现象均消失,涡流附着圆柱,且同圆柱一起高速旋转升力系数再次稳定.对应的升力系数时程曲线见图3.

图2 不同转速比α下的尾流图(Re=200)

图3 Re=200不同转速比下的升力系数时程曲线

随着旋转速度增加,尾流从漩涡脱落到稳定尾流、反向稳定尾流、单边涡和附着涡依次变化.尾涡结构形态对应不同的升力特性.对当前Re=200下的旋转圆柱绕流结果进行归整,不同尾流结构的范围如下：漩涡脱落(0≤α<2),稳定尾流(2≤α<3.5),反向稳定尾流(3.5≤α<4.4),单边涡(4.4≤α<4.8)和附着涡(α≥4.8).

图4为Re=200下升阻力系数均值随转速比的变化。由图4a)可知:平均升力随着转速的增加而急剧增加，当前结果表明升力系数可以超过“普朗特极限值”。在0≤α≤4.8(除附着涡区域外)处,平均升力和转速之间的抛物线关系，在α≥4.8处,该关系变化为近似线性关系，拐点对应于第二不稳定区域的末端.由图4b)可知:随着转速比增大,平均阻力系数先减小至接近0,然后迅速增大,这与文献[18]的结论相似.而且在第二不稳定区4.4≤α≤4.7,它的增长速度快于α≥4.8.类似地,第二不稳定区的终点是平均阻力的拐点，从平均阻力系数随着旋转比变化趋势可知,在较大旋转比下,平均阻力系数逐渐增大，表明在高旋转比下,平均阻力系数可能具有同升力系数相当的量级值.

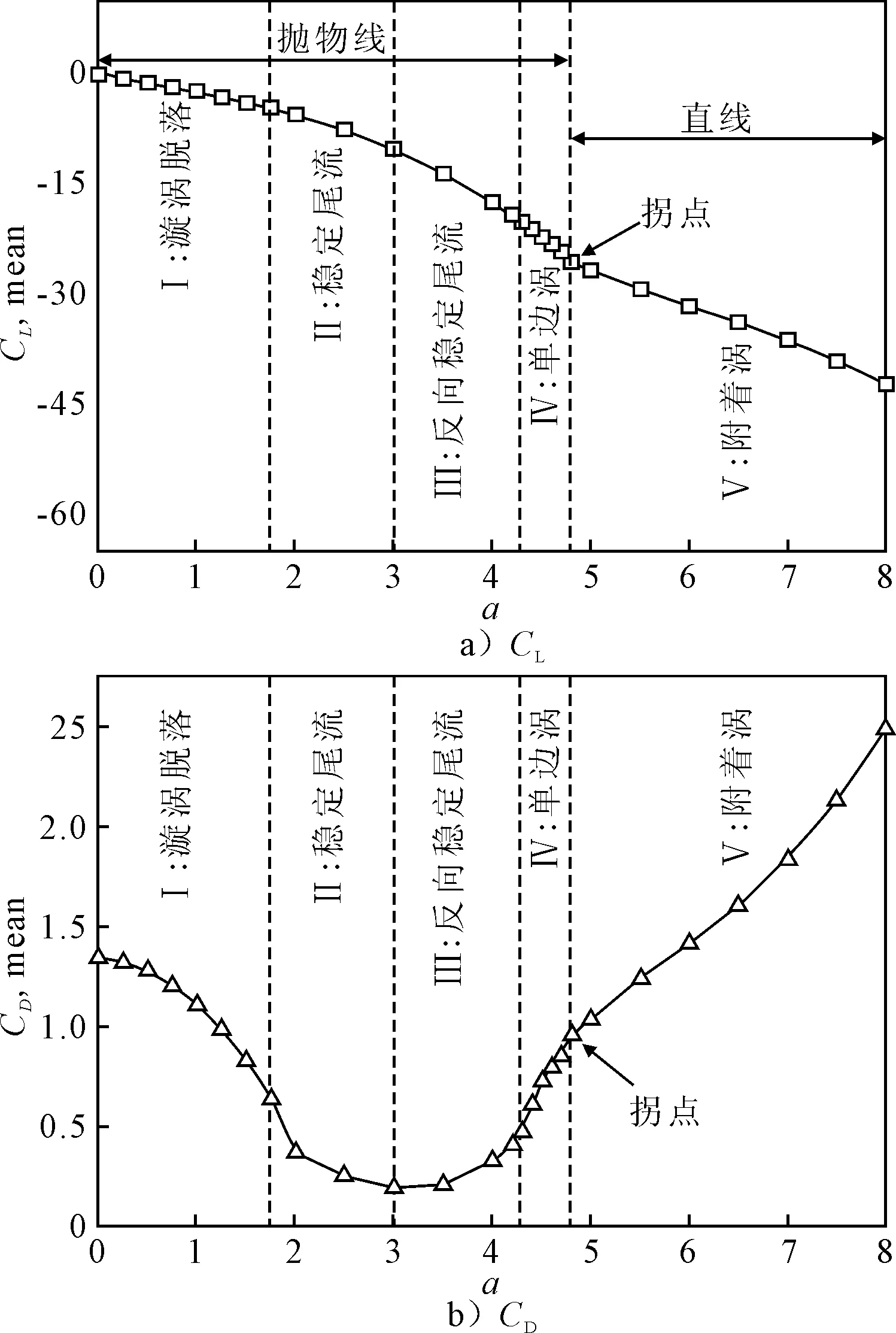
图4 Re=200下升阻力系数均值随转速比的变化

图5为不同旋转比下升阻力系数频率，图6为Re=200下升阻力系数频率随旋转比的变化.

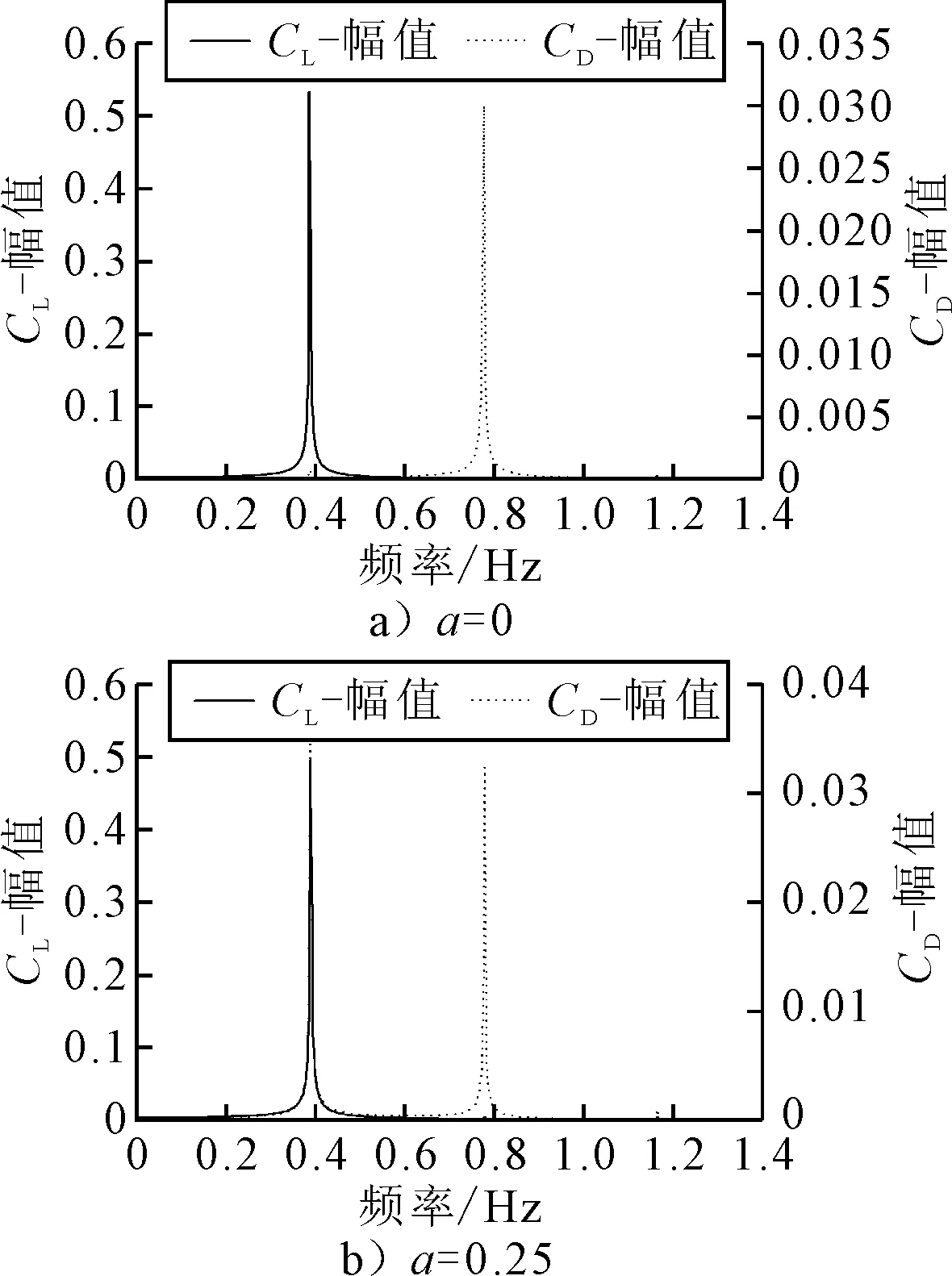
图5 不同旋转比下升阻力系数频率

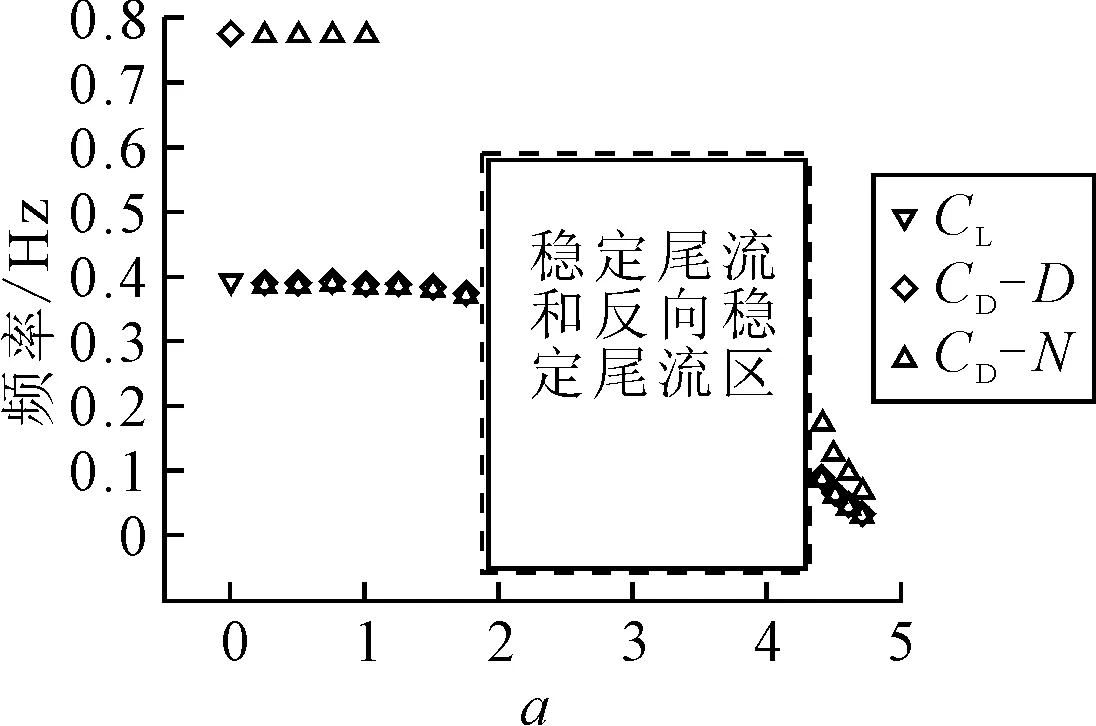
图6 Re=200下升阻力系数频率随旋转比的变化

由图5～6可知:当α=0时,阻力系数的峰值频率为0.78 Hz，升力系数的峰值频率为0.39 Hz,即阻力系数的峰值频率为升力系数的2倍，随着圆柱旋转,升力和阻力系数的主频率相等,但阻力系数的2倍频率依旧存在,且不可忽略.当α=0.25时,阻力系数具有两个峰值频率：主频率0.39 Hz(与升力系数相等)和0.78 Hz.造成升阻力主频率相等的原因是由于尾涡的倾斜,诱导的起伏压力不仅在横向有周期性的力成分(升力),在顺流向也有周期性的力成分(阻力)，阻力系数存在两个峰值频率的现象在1<α≤1.75范围内消失,在第二不稳定阶段(4.4≤α<4.8)再次出现.

图7为Re=200下升阻力系数幅值与斯特劳哈尔数随转速比的变化。在第一不稳定阶段,随着旋转速度的增加,升力幅值保持稳定然后减小,阻力幅值逐渐增加，倾斜的涡旋脱落是导致升力和阻力幅度逐渐接近的原因.在第二不稳定阶段,随着转速的增加,升力幅值增加,而阻力幅值减小，斯特劳哈尔数在第一不稳定阶段有微幅减小,均值约为0.194.与第一不稳定阶段相比,第二不稳定阶段的斯特劳哈尔数要小得多,且急剧下降.

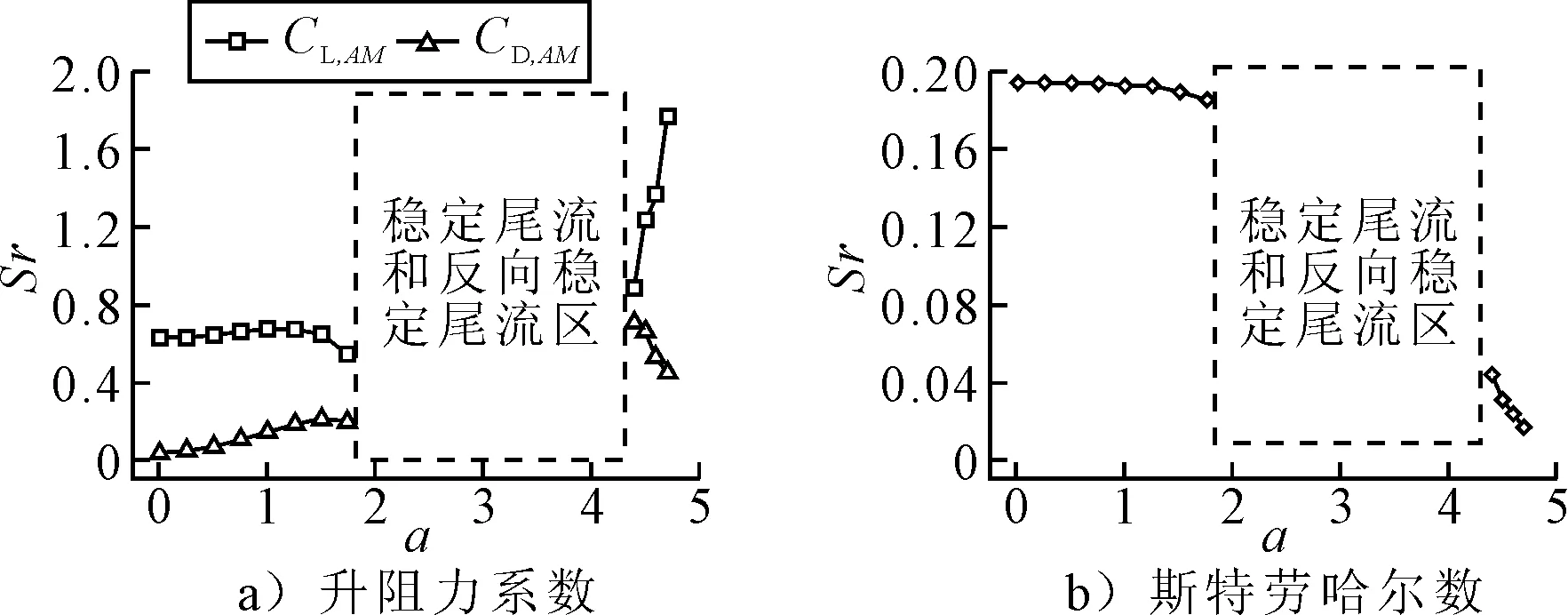
图7 Re=200下升阻力系数幅值与斯特劳哈尔数随转速比的变化

3.2 湍流结果及对比分析

Re=3 900下的尾流结构见图8.存在五种不同的尾流形态：①漩涡脱落,周期性地从圆柱上脱落两个反向涡流,为2S模式(每个周期有两个单涡流脱落),随着转速的增大,尾涡被拉长,且尾涡向旋转方向产生倾斜;②稳定尾流,漩涡脱落消失,尾流由一正一负两层涡形成,且负涡位于正涡之上.这两个阶段与层流状态下一致;③三层稳定尾流,由于湍流效应及旋转的存在,尾流由两正一负三层涡形成,且负涡位于两正涡之间;④单边三涡,再次出现涡脱落现象,且与层流存在明显差别,在圆柱旋转侧有三个涡脱落(两正一负),且脱涡频率较2S模式的低;⑤半附着涡,此阶段尾涡结构与层流的附着涡存在明显区别,除附着涡外,在圆柱旋转侧存在一正一负两层涡,且负涡位于正涡之上.

图8 不同转速比α下的尾流图( Re=3 900)

图9为不同雷诺数下升阻力系数均值随转速比的变化.由图9a)可知:在Re=3 900下,升力系数均值随旋转比的增大而增大,在第二不稳定阶段前(0≤α≤4.16),升力系数均值与旋转比存在抛物线关系,在第二不稳定阶段后(α≥4.21),可以观察到升力系数均值与旋转比的直线关系.由图9b)可知:在Re=3 900下,阻力系数均值随转速比的增大先减小后增大.对比层流情况下升阻力系数均值变化可知,在两种流动状态下升阻力系数均值随旋转比的变化规律一致,但湍流情况下变化速率较慢，且由于湍流情况下黏性力较层流小,湍流阻力系数均值基本小于层流.

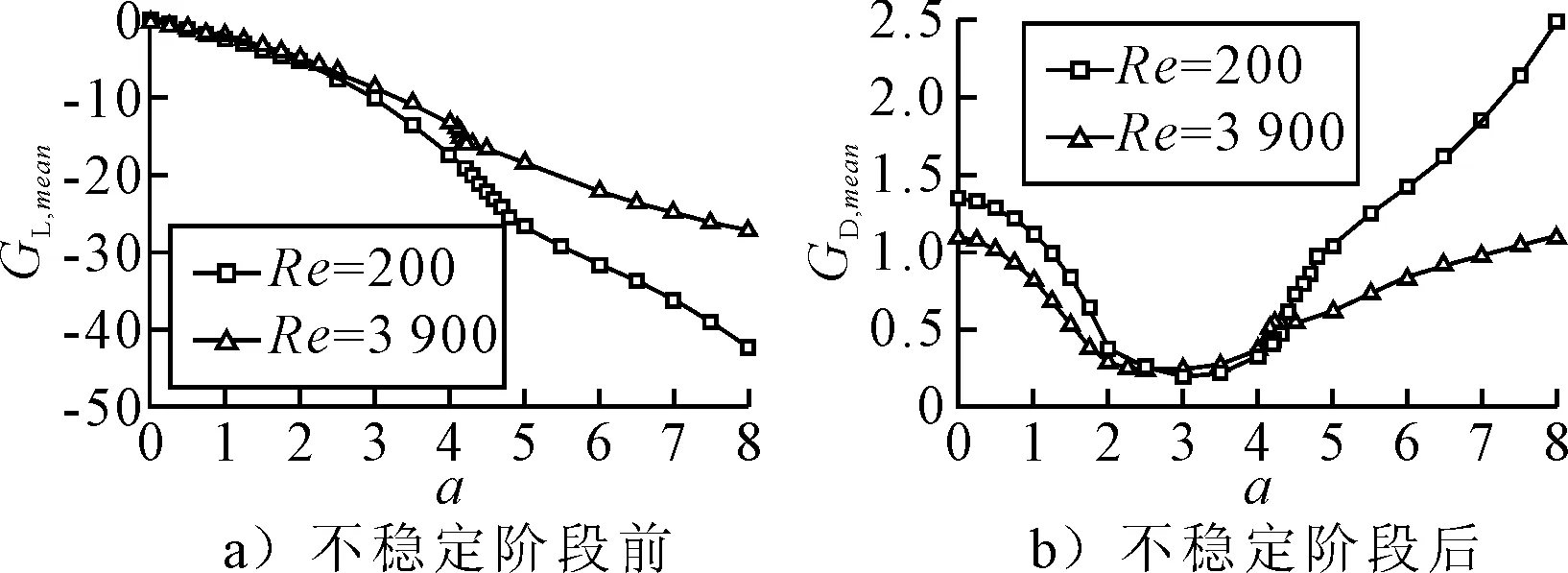
图9 不同雷诺数下升阻力系数均值随转速比的变化

不稳定阶段的升阻力幅值见图10.在第一个不稳定阶段,Re=3 900下随着旋转比α的增大,升力系数幅值先小幅增加后明显减小,阻力系数幅值先增大后减小.在第二个不稳定阶段,升力系数幅值随旋转比α的增大而增大,阻力系数幅值随旋转比α的增大而减小.升阻力系数幅值随旋转比的变化趋势在两种流态下保持一致,但在第一不稳定阶段,湍流情况下升力系数幅值减小速率较层流要快.

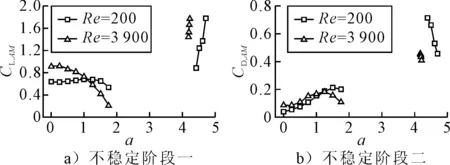
图10 不同雷诺数下升阻力系数幅值随旋转比的变化

不稳定阶段的斯特劳哈尔数见图11。对于第一个不稳定状态,湍流情况下Sr大于层流,二者均随旋转比增加而减小,且Re=3 900减小速率更快.在第二不稳定阶段,湍流情况下Sr明显小于层流,二者均随旋转比增加而减小,且均比第一不稳定阶段的Sr小得多.因流动状态的影响,第二不稳定阶段的生成范围从到向前移动,且湍流第二不稳定阶段范围宽度远小于层流,由(4.4≤α≤4.7(Re=200)变为4.16≤α≤4.21(Re=3 900)).

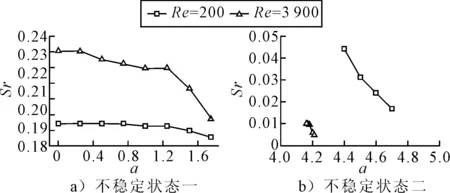
图11 斯特劳哈尔数随转速比的变化

4 结 论

1) 随着旋转比的增加,两种流态下均可发现五种尾流结构.层流状态下为：漩涡脱落、稳定尾流、反向稳定尾流、单边涡和附着涡.湍流状态下为：漩涡脱落、稳定尾流、三层稳定尾流、单边三涡和半附着涡.

2) 层流与湍流情况下,水动力系数随转速比的变化规律一致,升力系数均值增大,阻力系数均值先减小至接近零,随后增大,升力系数幅值在第一不稳定阶段先小幅增大后减小,第二不稳定阶段增大,阻力系数幅值在第一不稳定阶段先增大后减小,在第二不稳定阶段减小.与层流相比,湍流情况下升阻力系数均值随旋转比变化速率较缓.

3) 由于圆柱的旋转,升阻力系数频率关系由2倍关系变为阻力系数主频率与升力系数频率保持一致,且阻力系数在一定的旋转比范围内存在不可忽略的2倍频率.斯特劳哈尔数随转速比的增大而减小,且第二不稳定阶段的Sr值要小很多.湍流情况下的Sr值随旋转比的变化更为明显，与层流相比,湍流第二不稳定阶段的生成范围前移,且范围宽度远小于层流.