基于日光诱导叶绿素荧光的陆地总初级生产力估算
袁艳斌 张城芳,2 黄 鹏 董 恒 杨敬豪
(1.武汉理工大学资源与环境工程学院,武汉 430070;2.武汉华夏理工学院土木建筑工程学院,武汉 430223)
0 引言
总初级生产力(Gross primary productivity,GPP)是指单位时间内植物通过光合作用吸收CO2过程固定的有机碳量,是理解大气-生物圈相互作用和全球变化的关键参数,也是目前全球碳循环研究中最大不确定性来源[1]。准确估算全球和区域尺度的陆地GPP对于研究全球碳循环和对气候变化的反馈具有重要意义[2]。
目前区域或者全球尺度的GPP估算主要有3种方法[3]:结合通量站点数据、遥感产品和网格化气候产品等的机器学习方法;结合遥感获取的植被绿度信息和气象变量的光能利用率模型;气象资料驱动的生态过程模型。其中基于植被指数的光能利用率模型是当前最主要的GPP估算方法。该类模型中最常用的如归一化植被指数(NDVI)、增强植被指数(EVI)等基于反射率的植被指数可以代表植被的“绿度”和光合能力,但当冠层叶绿素含量较高时会造成反射率信号饱和,导致基于遥感反射率数据估算植被冠层吸收的光合有效辐射比例(Fraction of absorbed photosynthetic active radiation,fAPAR)仍然是一个挑战。另外,这些植被指数对尚未引起反射率数据变化的光合活动(例如改变气孔导度、光反应中心开放比例、热耗散比例调节等)极不敏感,与实际植物短期内光合作用关联性不强,单独使用反射率数据并不能及时、准确地反映植被的光合作用和受胁迫状况的变化[4-5]。该模型中参数光能利用率(Light use efficiency,LUE)也是可变的,取决于物候状态、结构和物种组成等因素,目前LUE参数化不足被认为是光能利用率模型不确定性的主要来源之一[6]。生态过程模型虽然有很强的植物生理机理,但是模型之间的物理机理差异很大,且输入参数众多难以获取,运行的空间分辨率很低,GPP估算精度较差。以上诸多模型参数化和解释变量的不确定性限制了基于遥感进行全球GPP估算的准确性[3]。因此,需要探索一种新的能直接关联植物光合作用的GPP估算方法。
叶绿素荧光是绿色植物在吸收光能后进行光合作用时重新释放的红光和近红外光子。植被在自然光照下发射日光诱导叶绿素荧光(Solar-induced chlorophyll fluorescence,SIF)信号,可以看作植被瞬时光合作用活动的理想探针[7-8]。由于SIF是由植被产生,相对于反射率数据来说,与植被光合作用具有更紧密的联系。LEE等[9]发现,即使叶面积保持不变,SIF也可以捕获干旱胁迫导致的森林光合作用的下降,从而证实被动测量SIF可用于跟踪大尺度下,没有绿度和结构变化时,植被生理活动的变化。近些年随着SIF遥感提取算法的发展,大量卫星平台上的高光谱分辨率光谱仪已用于提取近红外波段的SIF,并提供了不同空间和时间尺度的SIF产品[10],开辟了监测植物实际光合作用和估算陆地生态系统GPP的新途径[11]。目前基于SIF的GPP估算研究,多集中于验证来自于不同传感器的大尺度范围内的SIF数据在不同植被类型上与GPP的高度相关性,证明了SIF估算陆地GPP具有巨大潜力[12-15]。建立SIF与GPP估算模型的研究,还处于起步研究阶段。大多数估算方法是基于两者之间较高的相关性,直接构建SIF与GPP建立线性回归模型。最有代表性的是GUANTER等提出的GPP-SIF线性估算模型[11,16]。然而,越来越多的实验证明,SIF与光合作用的直接联系受到很多因素影响,荧光产率和光化学速率的关系复杂,且在不同的空间尺度和时间尺度的变化并不明确,SIF-GPP线性模型缺乏普适性[15]。关于SIF-GPP关系是否仅反映SIF和光合有效辐射(Absorbed photosynthetic active radiation,APAR)之间的关系,或者SIF是否还包含关于LUE的信息机理性问题也存在很大的争议[17]。因此需要研究GPP-SIF的关联关系在不同时空尺度上的变化,和其受到的环境胁迫、冠层结构、植物功能型等多种因素的影响,在GPP-SIF经验线性估算模型的基础上,引入影响植被光合能力或者GPP-SIF关系的因素,以构建更具普适性的GPP估算模型。本文从叶绿素荧光的发射机理出发,在GPP-SIF经验线性估算模型的基础上,引入一些影响植被光合能力或者冠层SIF发射的因素,以构建更为精确的基于近红外SIF的GPP估算模型,为更好地监测GPP提供新的途径。
1 基于近红外叶绿素荧光的GPP估算模型构建
冠层尺度上红光荧光的重吸收受冠层结构和叶绿素浓度影响,叶片内部的吸收率超过90%,其冠层逃逸率较难确定。近红外荧光由于不处于叶绿素吸收光谱范围内,其基本上不受重吸收作用影响,当冠层结构愈复杂或叶绿素浓度增加时,近红外荧光更是优于红光荧光。另外,目前大部分从卫星平台提取的SIF均集中在近红外波段,红光波段SIF的反演精度远低于近红外SIF[18-19]。因此,本文选择近红外荧光建立GPP反演模型。
近红外荧光SIFNIR表达式为
SIFNIR=PARfAPAR(aⅡΦFⅡFPSⅡ(λNIR)+
aⅠΦFⅠFPSⅠ(λNIR))(1-pr(λNIR,Chl))
(1)
式中PAR——光合有效辐射
fAPAR——植物冠层吸收的光合有效辐射比例
ΦFⅠ——PSⅠ的荧光发射产率
ΦFⅡ——PSⅡ的荧光发射产率
FPSⅡ(λNIR)——荧光发射光谱中波长函数,代表PSⅡ的荧光发射光谱的形状
FPSⅠ(λNIR)——荧光发射光谱中波长的函数,代表PSⅠ的荧光发射光谱的形状
aⅠ——光系统群Ⅰ的相对吸收截面积
aⅡ——光系统群Ⅱ的相对吸收截面积
pr(λNIR,Chl)——近红外波长的荧光在叶片内和在冠层内被重吸收的比例
λNIR——近红外波长
光能利用率模型的一般表达式为
GPP=APARLUEP=PARfAPARLUEP
(2)
式中LUEP——植物的光能利用率
APAR——植物在400~700 nm范围内吸收的光合有效辐射
联立式(1)、(2)得到GPP与SIFNIR之间的关系为

(3)
对于光系统PSⅠ而言,其叶绿素荧光效率在光照条件下一般比较低,且很少受光化学和非光化学淬灭过程的影响,故式(3)中的aⅠΦFⅠFPSⅠ(λNIR)可认定为常数。另外,光系统PSⅡ是调节和影响植物光合效率的主要机构。根据FRANKENBERG等[17]基于脉冲式调节荧光仪(Pulse amplitude-modulated fluorometers,PAM)主动叶绿素荧光测量研究发现,当未出现严重的胁迫情况致使调节性能量耗散量子产量ΦNPQ急剧增强时,光化学产率ΦP+ΦNPQ和荧光产率ΦF大致恒定,当光照条件不是光合作用的限制因素时,ΦP的变化主要由kNPQ的调节机制控制,ΦF与ΦP的耦合关系不明显。故在未出现严重胁迫情况下和在未出现光照条件限制光合作用的情况下(当前卫星平台获取的SIF均处于10:00或13:00左右,在晴朗天气不会出现光合作用的光强限制),PSⅡ的叶绿素荧光产率可以认为是恒量,因此式(3)中的aⅡΦFⅡFPSⅡ(λNIR)也可以认为是常数。
1-pr(λNIR,Chl)表示近红外荧光在离开冠层时受到重吸收和散射的影响。文献[11,20]认为近红外荧光的重吸收比例很低,但冠层结构对近红外荧光的散射依然存在很大的影响。故本文引入能反映植被冠层结构的植被指数来表达这种影响作用,且引入的植被指数应尽量表达冠层的叶面积指数信息,而尽可能少地携带冠层叶绿素浓度信息。
当接收的光能超过自身的可利用能力,作物将通过叶黄素循环进行调节,在色素转换的过程中将激发能量以热能的形式耗散,并改变以531 nm为中心的窄波段内的反射率变化特征。光化学反射指数(Photochemical reflectance index,PRI)正是这变化特征的定量表示[21]。越来越多的研究表明,PRI可通过非光化学淬灭(Non-photochemical quenching,NPQ)的相关性来追踪LUEP的变化[22],在叶片、冠层和景观尺度上基于遥感获取的PRI与LUEP均存在良好的相关性,PRI可以作为LUEP的遥感估算[23]。但两者的关系同样受到了冠层结构和冠层叶绿素含量的影响。由于每一种植被类型的光合能力不同,其光能利用率的最大潜力随着植物种类而变,故本文引用光能利用率模型中的最大光能利用率εmax,且在PRI与LUEP的关系中引进能反映冠层光学结构的植被指数。LUEP的计算公式为
LUEP=εmaxPRIf(VIs)
(4)
式中f(VIs)——植被冠层结构特征的影响函数,这种影响主要是由冠层叶面积指数造成
PRI——光化学反射指数
εmax可以采用MODIS土地利用覆盖产品MOD12Q1中的UMD分类标准确定。
综上所述,本文构建的基于近红外荧光的GPP估算模型的表达式为
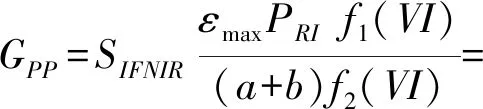
(5)
式中C——不同植被类型拟合常数
f1(VI)——利用植被指数构建的PRI与LUE的合数关系
f2(VI)——利用植被指数构建的冠层结构对逃逸率的影响函数
2 数据与方法
2.1 GOME-2 SIF荧光数据
采用SIF数据是由搭载在MetOp-A卫星上的GOME-2传感器的第四通道(波长范围为734~758 nm,光谱分辨率为0.5 nm)所提取的GOME-2 SIF740荧光产品,版本为V27[19]。该产品分为level 2和level 3两个级别,level 2是日尺度的叶绿素荧光产品,分辨率在2013年7月之前为40 km×80 km,之后为40 km×40 km,level 3是在日尺度的SIF产品上进行了时间上和空间上一系列处理得到的空间分辨率为0.5°×0.5°的月尺度叶绿素荧光产品。
本文下载了2008—2014年日尺度和月尺度的GOME-2 SIF产品。一方面,由于月尺度SIF的空间分辨率与通量塔的辐射范围存在巨大的不匹配,为了减少这种不匹配性,本文先采用像元分辨率为40 km×40 km的日尺度SIF,结合GOME_F算法对日尺度SIF进行综合后得到SIF月值产品,再根据通量站点坐标信息批量提取各站点所处GOME-2像元的月尺度SIF数据。另一方面,在估算全球某年中每月的GPP分布时,采用level 3的月尺度SIF数据(https:∥avdc.gsfc.nasa.gov/pub/data/satellite/MetOp/GOME_F/)。
2.2 通量站点与数据
采用来自全球通量观测网发布的FLUXNET2015数据集的2008—2014年的日尺度和月尺度的GPP数据,其产品标识为“GPP_NT_VUT_REF”(http:∥fluxnet.fluxdata.org/)。由于通量塔观测的范围与GOME-2的粗分辨率(40 km×40 km)不匹配,为了选择能较好代表GOME-2像元的通量站点,参照ZHANG等[24]的做法,采用空间分辨率为0.05°的土地覆盖类型产品(MCD12C1)和月尺度EVI植被指数(MOD13C2),用于确定像元内的景观同质性。另一方面,为了植被类别和模型应用的方便,参照FRANKENBERG等[25]做法将土地覆盖类型产品MCD12C1中的国际地圈生物圈计划(IGBP)全球植被分类方案进行合并,形成7类植被覆盖类型:针叶林(NF,包括常绿和落叶针叶林)、常绿阔叶林(EBF)、落叶阔叶林(DBF,包括混合森林)、灌木林(SHR,包括郁闭和稀疏灌木林)、热带稀树草原(SAV)、耕地(CRO)和草地(GRA)。本文最终选用了19个站点,其空间位置和景观同质面积占比、EVI标准差等信息见表1。

表1 各通量站点的基本信息Tab.1 Basic information of each flux site
有些植被类型例如耕地、落叶阔叶林、草地等,在生长季节之外往往是没有绿色植物覆盖地表的。处于生长季之外的日期虽然通量站点依然会监测GPP数据,但该数据由于模型自身局限性而多为负值,不能代表真实情况。所以本文先依据每个站点的日尺度GPP在一年中的分布情况,以大致确定不同站点所代表的植被类型的生长季节,然后将不属于生长季内的GPP数据删除,不参与模型拟合。
2.3 植被指数和MODIS地表反射率数据
本文所构建的模型采用两种植被指数:一种是用来估算植被LUEP信息的光化学反射指数;另一种是用来表达植被冠层光学结构的植被指数。对于近红外SIF而言,主要受冠层叶面积指数、叶倾角分布等冠层结构的影响,故选择在反演冠层LAI上具有较好表现的植被指数,包括NDVI、EVI、修正土壤调节植被指数(Modified soil-adjusted vegetation index,MSAVI)以及近红外植被反射率指数(Near-infrared reflectance of vegetation,NIRv)等[26-29]。本文选取空间分辨率为1 km的MODIS地表反射率和植被指数产品来计算或获取植被指数。
对于PRI的计算,由于第11波段反射率(36~526 nm)数据暂时只提供日尺度产品(MCD19A1),所以先计算每个站点的日尺度PRI,然后采用均值法得到月尺度PRI。值得注意的是由于MODIS的波段设置中没有570 nm的波段,本文采用最靠近该波长处的波段Band4(545~564 nm)来计算PRI。对于NDVI、EVI、NIRv等植被指数,采用月尺度植被指数产品(MOD13A3),包括月尺度EVI、NDVI两个植被指数和红光、蓝光、近红外、中红外4个波段的月尺度反射率数据。根据各站点的空间位置提取了站点所处像元2008—2014年月尺度上的各植被指数信息,其计算公式见表2。

表2 相关植被指数的计算公式Tab.2 Formula of vegetation index
2.4 模型的非线性拟合
在本文所构建的模型中,PRI与LUEP的关系以及表征冠层结构的植被指数对SIF的影响在大多数情况下均不是呈线性比例关系。支持向量机回归以VC维理论和结构化风险最小化作为基本原理,可以解决小样本、非线性、高纬度和局部极小值点等常规回归拟合算法所不能处理的问题。运用向量机回归算法,并选用粒子群优化算法作为参数选择的策略,将VIs作为输入变量xk,将GPPEC/(SIFNIRεmaxPRI)作为输出变量yk,拟合式(5)中的非线性关系f。
3 结果与讨论
3.1 SIF740与通量站点GPPEC比较分析
图1为不同决定系数R2下7种植被类型各站点在月尺度上GPP与SIF散点图,不同颜色的点表示不同的站点,不同颜色的虚线表示线性回归拟合线,无线型对应的R2表示该植被类型全部数据的拟合精度,所有P<0.01。从图中可以看出7种植被类型的通量塔观测的GPP(GPPEC)和740 nm处荧光(SIF740)均呈现出一定的线性相关,不过不同的植被类型间两者的线性关系表现出较大的差异。总体而言,落叶阔叶林的表现最好,R2高达0.815 1,其次是热带稀疏草原、灌木丛、耕地和草地R2均大于0.4,针叶林和常绿阔叶林表现最差,R2均小于0.4,该结果与现有GPP估算模型在不同植被类型上的估算精度大致类似[30]。
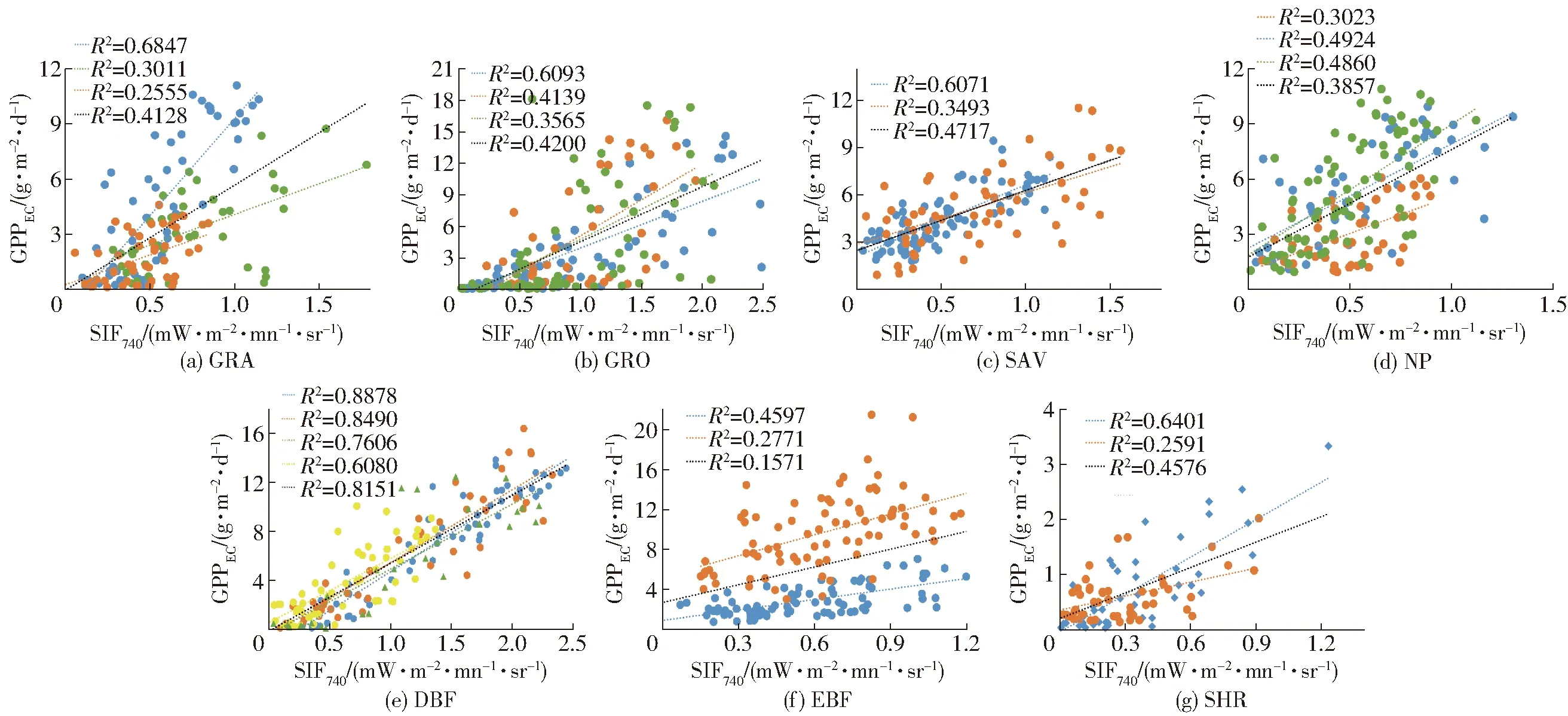
图1 不同植被类型的通量站点月尺度GPP数据与月尺度SIF的线性关系Fig.1 Linear relationships between monthly GPP data and monthly SIF of flux sites for different vegetation types
另一方面,在同种植被类型不同站点之间,GPPEC和SIF740的线性关系也存在较为明显的差异,例如在草地相关性最高的站点R2高达0.684 7,而最差的站点R2只有0.26,同样的现象也出现在耕地、热带稀疏草原和灌木丛中。对于草地和耕地可以发现,不同站点线性拟合的斜率存在较大的差异,这主要是由不同的耕地种植的作物品种和不同草场的草种不同引起的。对于落叶阔叶林而言,不同站点的相关性均比较高,而且线性拟合的斜率很接近,这主要是因为落叶阔叶林带的植被层次结构简单,一般分为乔木层、灌木层和草本层,且植被覆盖随季节变化大,物候特征明显且类似。对于常绿阔叶林而言,其结构复杂,多处于高温多雨地带,受云量、干湿季节影响严重,目前所有GPP估算模型在常绿阔叶林的估算精度都不理想。对于稀疏热带草原而言,以木本低矮灌木为主,大多数生长在植被稀疏地区或者荒漠戈壁等干旱地区,且存在范围内分布不均匀,成丘团状分布,其平均覆盖度低于 30%,不同站点植被覆盖的密度不同,这也是导致其GPPEC和SIF740在不同站点呈现差异的主要原因,另外由于其水分缺失,不利于光合作用,GPP较低,在通量测量时会带来很大的不确定性。
从不同植被类型的站点GPPEC和SIF740散点图可以发现:GPP-SIF关系对植被类型具有依赖性,也可以从某种程度上佐证在GPP-SIF的线性关系中引进植被冠层结构和光合能力等影响因素的必要性。
3.2 应用不同植被指数的模型估算精度分析
本文应用NDVI、EVI、MSAVI、NIRv和相关组合指数构建第2节中提出的模型,分别利用各植被类型所有站点数据和单独利用各植被类型中GPPEC和SIF740线性关系最佳站点数据,结合支持向量机回归算法,验证了模型估算的GPPmodel与通量站点GPPEC的相关性,结果见表3。可以发现,与SIF-GPP经验线性模型相比,无论是单个站点还是综合了同种植被类型的多个站点,引进了表示冠层结构影响的植被指数和本文所构建的PRI模型,除了在落叶阔叶林有稍微下降以外,在所有的植被类型上估算精度都有了很大的提高,特别是在耕地上,预测精度基本都有30%以上的提升。由于经验线性关系能很好地表示落叶阔叶林的GPP与SIF协变特征,两者相关性高达0.815,且不同站点之间的差异性不大,故本模型对其估算精度改进不明显,相关性处于0.757~0.797之间。不过本模型对常绿阔叶林的估算精度依然较低,GPPmodel与GPPEC的相关性处于0.15~0.3之间,这主要跟常绿阔叶林的生态结构和受环境影响复杂性有关,准确估算常绿阔叶林的GPP也是目前一个挑战。
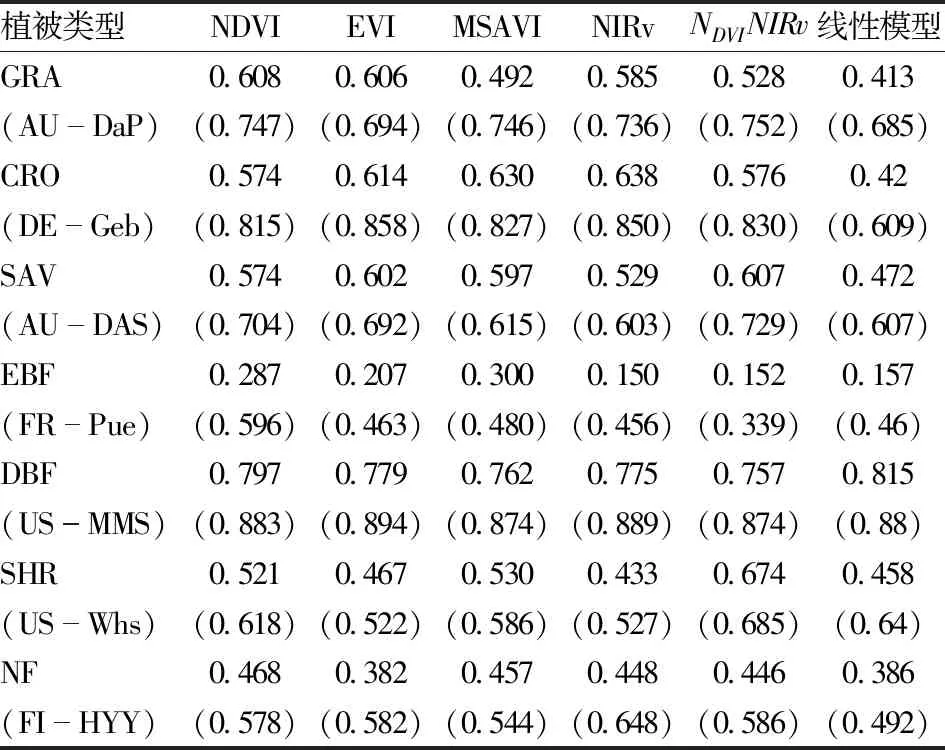
表3 不同植被指数模型对各植被类型GPPmodel与GPPEC的R2估算Tab.3 Application of different vegetation index models for various vegetation types to estimate R2 between GPPmodel and GPPEC
另一方面,本模型对将某植被类型所有站点作为整体的提升效果,明显优于将各植被类型中GPPEC和SIF740线性关系最佳单个站点的提升效果。这主要是因为εmaxPRI和植被指数的引入,从某种程度上消除了单个站点由冠层结构、覆盖密度和植物种类等的不同对GPP-SIF关系带来的差异性,从而使该植被类型内各站点的GPP-SIF关系趋于相似,提高了GPP估算精度。但同时得指出,本模型在单个站点的估算精度远高于同种植被类型内多个站点混合在一起的估算精度。以应用NDVI为例,GPPmodel与GPPEC在耕地和落叶阔叶林上的决定系数高达0.8以上,在草地、稀疏草原上达0.7以上,即使是针叶林和常绿阔叶林也接近0.6。
本文选用不同的植被指数来构建模型,总体而言,NDVI、EVI、MSAVI和NIRv在模型中应用的效果差异性不大,这主要是因为这4个植被指数均能较好地表达植被冠层的叶面积指数信息。但是不同指数在个别植被类型中的表现有较大的差异,例如NDVI对常绿阔叶林估算精度的提升效果远优于其他3个指数,NIRv对常绿阔叶林和热带稀疏草原的提升效果较差,EVI对灌木林的提升效果不明显。
图2为应用本文模型估算各植被类型中GPPEC和SIF740线性关系最佳站点的GPPmodel和该站点实测GPPEC在季节上的变化曲线。可以发现,在所有单个站点中,本文模型都可以很好地体现各站点所代表的不同植被类型GPP的季节性变化特征。特别是在植被类型为落叶阔叶林的US-MMS站点上,GPPmodel和GPPEC随时间变化的曲线高度吻合,这是由于落叶阔叶林明显且稳定的季节特征。在植被类型为耕地的DE-Geb站点上,GPPmodel和GPPEC变化区域吻合度也较高,但是在GPP峰值时间段内,GPPmodel出现了峰值高估的现象。在针叶林的FI-HHY站点、灌木丛的US-Whs站点和热带稀疏草原的AU-DAS站点上,GPPmodel虽然表示了季节变化特征,但均出现了低估现象。

图2 在单个站点上模型估算月尺度GPPmodel与地面监测月尺度GPPEC的时间变化曲线Fig.2 Time changes of model estimated monthly GPPmodel and ground monitored monthly GPPEC at single site
综上两方面所述,本文在GPP-SIF经验线性模型基础上引入PRI和植被指数所提出的模型,无论是在同种植被类型多个站点还是在单个站点的估算精度,较经验线性模型均有较大程度的提升,且估算结果可以很好地表示GPP的季节变化特征。故本文模型在月尺度的GPP估算方面在一定程度上取得成功,能提高GPP在空间分布和时间分布上的估算精度。
3.3 基于模型估算的GPP全球分布格局
为了验证本研究所提出的理论模型在全球尺度上的应用效果,利用2010年的0.5°全球月尺度GOME-2 SIF产品和全球月尺度NDVI数据,估算了2010年各月的GPP数据集,并整理出2010年全球GPP分布情况,具体见图3。其中用2010年各同种植被类型通量站点的PRI月平均值,表示全球范围内所有该种植被类型分布地区的月尺度PRI,并将模型在每月估算中产生的负值调整为零。本文模型对2010年全球的GPP估算结果为每年128.86 Pg。根据BEER等通过结合全球通量观测数据和多种生态过程模型给出的全球GPP估算值的范围(123±8)Pg[1]可知,本文模型估算结果具有可靠性。

图3 基于本文理论模型估算的2010年GPP全球空间分布Fig.3 Estimated global spatial distribution of GPP in 2010 based on proposed theoretical model
4 结束语
本文模型与经验线性估算模型类似,在落叶阔叶林上估算精度最高,在针叶林和常绿阔叶林上估算精度较差。但无论是在单个站点上还是在综合同种植被类型的多个站点上,本文模型在所有植被类型上的估算精度都比经验线性估算模型有了很大的提高,且在将某植被类型所有站点作为整体时的提升效果,明显优于最佳单个站点的提升效果。另一方面,本文模型能较好地体现各站点所代表的不同植被类型GPP的季节性变化特征。

