基于模糊聚类分析法的学生成绩分类

于海洋，李秀文

（1.大连民族大学机电工程学院，辽宁大连 116600；2.大连民族大学理学院，辽宁大连 116600）

随着科技的进步，智能化阅卷也随之快速发展起来，为具体掌握考生的学习情况，需要通过一种科学规范的方法对试卷各个部分的得分进行系统分析。通过对考生试卷数据进行模糊聚类分析[1]，最终可得出一个相对合理的分类[2]。

模糊聚类分析是一种研究分类问题的数据分析方法[3]，是解决实际问题经常使用的数学工具之一。目前，模糊聚类分析方法已渗透到社会生活的方方面面，广泛地应用于商业、地质、农业、林业等多个领域，所以研究模糊聚类分析是非常重要的。本文主要选取了自动化专业五位学生的专业课期末考试成绩，以试卷中填空、选择、简答、综合运用的成绩等四项数据作为统计指标，利用模糊聚类分析对试卷得分点进行研究，找出通过考试反映出的普遍问题，让考试成绩数据“告诉”我们更多有价值的事实，对于调整和改进教学活动有着积极的参考意义。

1 模糊聚类分析法

对现实世界中的事物进行研究时，通常需要将事物按照其固有的属性或事物间的相似程度来进行分类，从中可以发现事物间的规律，这是我们认识世界、改造世界的一种重要方法。在数学中将各类事物按照一定的标准对其进行分类的方法称为聚类分析[4]，聚类分析是多元分析中的一种方法，它与回归分析、判别分析统称为多元分析的三大方法，聚类分析也是非监督模式识别的一个重要分支，它把没有类别标记的事物根据其相似性的准则对其进行适当的划分，从而把具有同种属性的事物区分开并加以分类。在对事物进行聚类的过程中，应使相似程度较大的事物尽可能归为一类，并且尽可能让类内事物的同质性最大化，而不相似的事物尽可能划分到不同的类中，并且尽可能让类与类间的异质性最大化，从而保证得到的同类事物类内事物间的相似程度最高。

聚类分析起源于分类学，它随着人类社会的产生和发展而不断深化，在古老的分类学中，人们主要靠经验和专业知识对事物进行划分，以便研究事物之间的特性以及它们的相似关系，很少利用统计学的方法，但随着生产技术和科学的发展，分类越来越细致，人们发现这种分类方法带有较强的人的主观性和任意性，并不能很好地揭示客观事物间内在的本质差别和联系，特别是当处理带有模糊性的分类问题时，一般而言模糊事物之间的界限并不是很清晰，常伴有模糊性。比如天气：阴天、晴天、下雨天之间就没有明确的界限，有时还会遇到“东边日出西边雨，道是无情却有情”这样的问题，且传统的聚类分析是一种硬划分，对类别划分的界限非常严格，面对此类带有模糊性的问题，传统的聚类分析方法根本没法实现，需运用模糊聚类分析方法[5]。

模糊聚类分析方法是用数学方法定量地确定样本的亲疏关系，从而客观地对现实生活中的事物进行分类，而且能够处理边界模糊的事物之间的分类问题[6]，在分类过程中，模糊聚类分析方法可以清楚地知道各个事物所属类别的模糊程度，从而能够建立起样本对于类别的不确定性描述，能更合理地反映现实世界。本文根据学生试卷的每个题型得分情况，运用模糊聚类分析对学生的成绩进行研究，对学生成绩的优劣做一个模糊归类。

2 数据处理

本文选取五位学生考试成绩为基本数据，试卷总分共100分，其中各题型所占分值分别为：填空20分，选择20分，简答20分，综合运用40分。将5名学生考试成绩组成一个集合X=｛x1,x2,x3,x4,x5｝（也称为论域X），分别标记为1号，2号，3号，4号，5号，则论域X=｛x1,x2,x3,x4,x5｝为被分类的对象。每个学生都以试卷填空、选择、简答、综合运用的成绩作为四项统计指标，即有：xij={xi1,xi2,xi3,xi4}，这里xij表示第i名学生第j项指标，则各学生成绩的原始数据矩阵为：

在实际问题中，如果数据不同，那么它们的量纲也会有所差别，为了比较不同量纲的数据，要将数据压缩在［0,1］区间上，这就需要对原始数据矩阵进行标准化。

通常有以下几种变换[7]：平移·标准差变换，平移·极差变换，对数变换。本文采用平移·极差变换进行数据标准化。

平移·极差变换

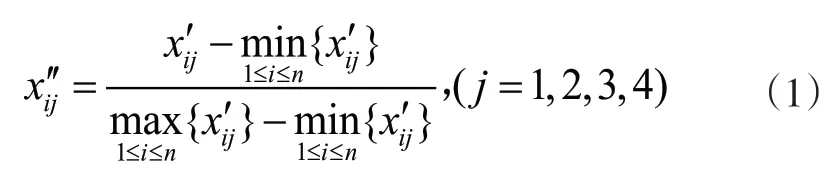
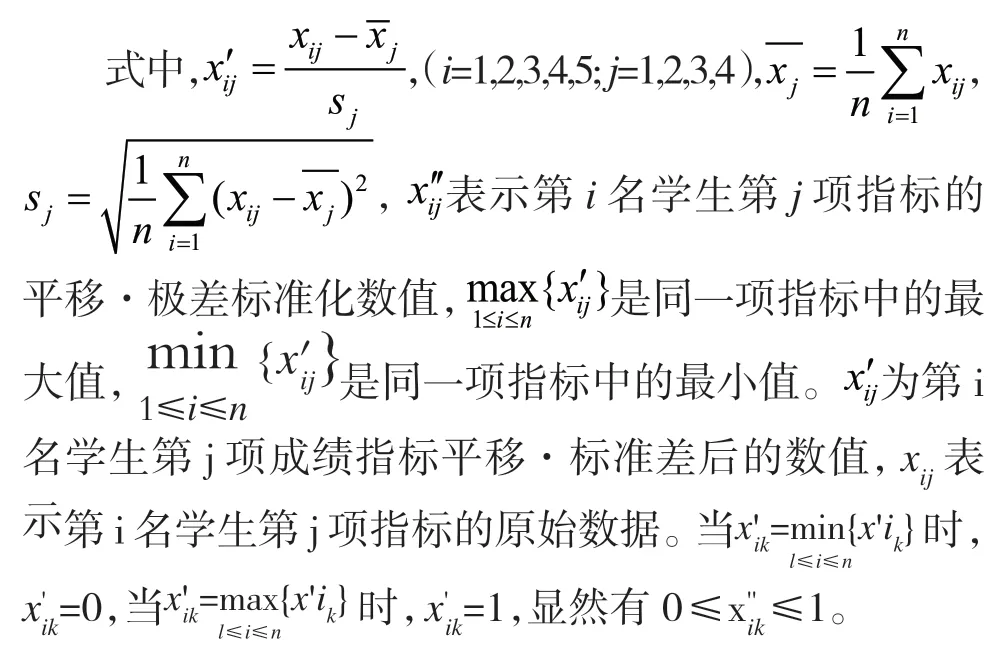
3 用最大最小法建立模糊相似矩阵

论域X={x1,x2,…,xn}，xi={xi1，xi2，…，xim}，依照传统聚类方法确定相似系数，建立模糊相似矩阵，xi与xj的相似程度rij=R（xi, xj）。确定Rij=R（xi,xj）的方法主要借用传统聚类的相似系数法、距离法以及其他方法[8]。具体用什么方法，可根据问题的性质选取。本文选取最大最小法建立模糊相似矩阵。

最大最小法的计算公式为：

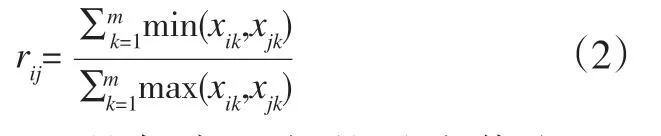
4 利用模糊等价关系进行聚类

聚类主要方法有基于模糊相似矩阵的直接聚类法（最大树法和编网法）和基于模糊等价关系矩阵的传递闭包法等。

模糊相似矩阵R满足自反性和对称性，但是并不满足传递性，那么要求等价矩阵，就要对矩阵R进行改造，就是求模糊相似矩阵R的传递闭包，我们只需要对R求平方即可，直到R22(n-1)=R22n。其中每作一次平方，我们就要对所得到的矩阵R22k作一次模糊相似矩阵，其目的是把rij压缩到[0,1]上，其方法和用最大最小法建立模糊相似矩阵一样。因为R2≠R，所以要再求R4，计算得到R4=R2，从而确定=R2为模糊等价矩阵。

利用模糊等价关系矩阵对5名学生进行聚类分析，截距水平λ从1降至0，按λ截矩阵进行动态聚类。

取λ=1时，则有：

由上面的矩阵可得，X被分为5类：{x1},{x2},{x3},{x4},{x5},即：{1号}，{2号}，{3号}，{4号}，{5号}。

降截距水平λ，对不同的λ做同样的分析，得到

当λ=0.6066时，则有：

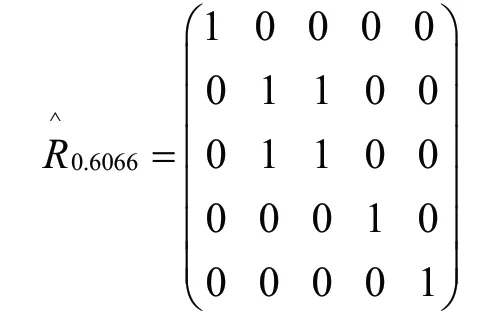
由上面的矩阵可得，X被分为4类：{x1},{x2,x3},{x4},{x5},即{1号}，{2号，3号}，{4号}，{5号}。

当λ=0.5395时，则有：

由上面的矩阵可得，X被分为3类：{x1}{x2,x3,x5}{x4}，即{1号}，{2号，3号，5号}，{4号}。

当λ=0.5313时，则有：

由上面的矩阵可得，X被分为2类：{x1},{x2,x3,x4,x5}，即{1号}，{2号，3号，4号，5号}。

当λ=0.1190时，则有：

由上面的矩阵可得，X被分为1类：{x1,x2,x3,x4,x5}，即：{1号，2号，3号，4号，5号}。

对于不同的截距水平λ对5名学生进行模糊聚类分析，得到不同的分类结果，聚类图见图1。

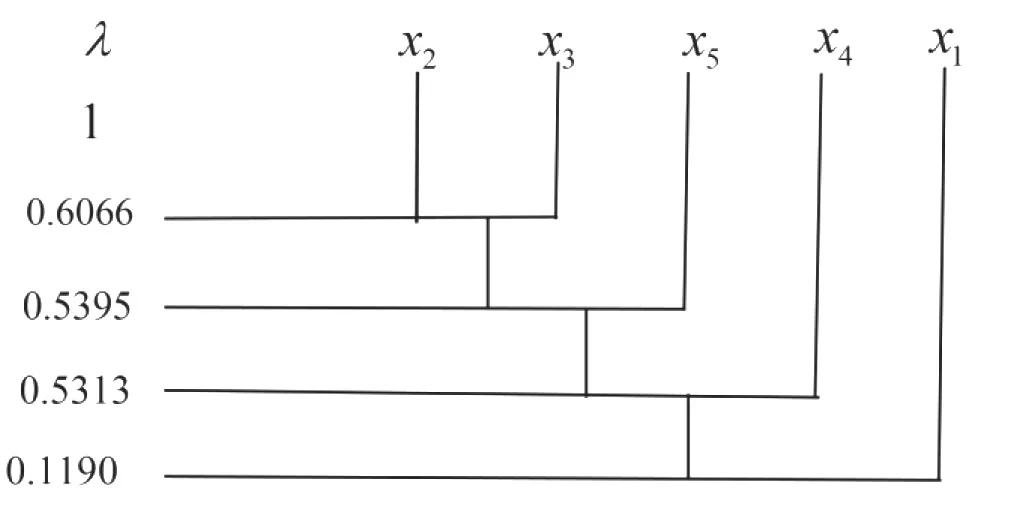
图1 聚类图

在分类过程中，可以看出若截距水平λ取值过高时，各学生试卷会各自分为一类；若截距水平λ取值过低时，又会使学生试卷聚为一类，为了更好地进行聚类分析，同时又能客观合理地反映学生之间的差别，按不同的截距水平λ对学生试卷进行研究。当0.6066≤λ≤1时，对5名学生进行分类，因为过于看重5名学生的各项基础指标，而忽略了各个指标之间关系相互影响的深浅程度，从而没有真正起到分类的作用，所以0.6066≤λ≤1的分类结果不理想。当0.5313≤λ≤0.6066时，分类结果能较好地体现出学生之间的差异，所以0.5313≤λ≤6066时的分类是科学可取的，说明分为一类的学生的学习成绩相似程度较为接近。

5 结语

通过对上述模型进行分析，序号为2，3的学生学习成绩优异，填空、选择、简答、综合运用四个方面都掌握得比较好，较突出；序号为5的学生填空、选择、简答、综合运用四方面的成绩较为良好，没有明显的弱项，全面发展，每个知识点都学习得很扎实，有很强的综合性。序号为1，4的学生学习成绩一般，填空、简答和综合运用的成绩较低，尤其是选择题失分太多，知识点掌握不好，需要全面提高。

本文利用模糊聚类分析法对学生试卷成绩进行分析，并不是直接按照整体考试成绩的高低分类，而是将试卷细化为各项指标进行对比，比传统的分类方法更加科学、合理。通过模糊聚类分析，找出试卷中反映出的普遍问题，使教师在今后的教学中更具有针对性，实现系统教学，有助于教师及时发现学生问题，高效提高学生成绩。