矸石充填开采工作面矿压显现规律研究

姚岐桦

（霍州煤电集团河津杜家沟煤业有限责任公司，山西 运城 043300）

引言

随着易开采煤层逐步完成开采，煤层开采的重点已经逐步向着赋存条件较为复杂的煤层转移，这使得煤层开采的效率得到了一定的制约。为了实现煤层的快速高效开采，我国学者提出固体充填开采技术，这项技术的核心是利用废弃矸石对工作面进行充填，控制巷道的覆岩，实现对经济和环保的兼顾。对拉充填工作面开采技术是在原有固体充填基础上的一种新的尝试，对拉充填工作面的稳定性是决定此项可否实施的重要因素，所以对对拉充填工作面的稳定性进行研究是十分重要的。李永明,刘长友[1]利用FLAC3D 数值模拟软对不同错距和充实率下围岩应力分布及巷道变形进行研究。研究发现，下工作面的超前段上隅角处支承应力集中较为明显，且随着错距的增大应力集中现象不断增强，当对拉充填工作面错距设定为5 m，充实率为90%时，此时固体充填开采效率最高。本文为了对对拉充填工作面稳定性进行研究，利用数值模拟软件对对拉充填工作面的矿压显现情况进行研究，为矿山安全生产提供一定的理论指导。

1 矿井概况及不同错距下巷道稳定性研究

杜家沟矿位于山西河津市清涧镇西北3 km，矿井设计生产能力60 万t/a，2-105 工作面主要开采2#、10#煤层，开采深度标高为+840 m～+600 m,井田呈不规则多边形，南北长4.6 km，东西宽4.5 km，面积9.89 km2。随着开采深度的增加，巷道不稳定等各种问题逐步凸显。

对拉填充工作面的矿压显现情况一般与对拉填充工作面的覆岩岩性、矸石压实性质、采高、错距长度等有关，所以在对其进行研究时需要单一变量，本文选定最佳错距长度5 m，对不同充实率下的对拉填充工作面围岩变形及覆岩的运移进行研究。首先选定杜家沟矿为研究背景进行数值模拟建模，数值模拟软件选定FLAC3D，根据实际地质情况建立模型的长宽高分别为450 m、235 m、36 m。根据地质情况对模型的力学属性进行设定，完成模型设定后对模型进行约束设定，将模型的地面进行固定，限制其水平及垂直方向的位移，对模型四边施加水平约束，限制其水平方向上的位移，同时设定工作面推进长度为300 m，设定模型的重力加速度为9.8 m/s2，在模型上端施加覆岩的自重10 MPa 的均布载荷，为了避免出现模型的边界出现边界效应，所以在模型的长宽分别留出50 m 和30 m 的边界，完成约束设定后对模性进行网格划分，网格划分对模拟十分重要，网格划分太粗影响模拟精度，网格划分过细加大计算时间且计算不易收敛，所以本文选定brick 建模单元，本构关系选定摩尔库伦模型，模型划分完成后共有301320 个单元和321456 个节点[2]。错距为5 m时对拉充填模型图，如图1 所示。

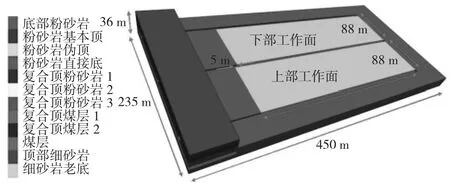
图1 错距为5m 时对拉充填模型图

2-105 工作面利用三条巷道布置两个同时工作的工作面，成为对拉工作面，模拟选定的错距为0、5、20 和50 m，选定充实率为90%进行研究，对不充实率下的矿压显现及运移规律进行研究，不同错距下巷道围岩应力分布情况，如第176 页图2 所示。

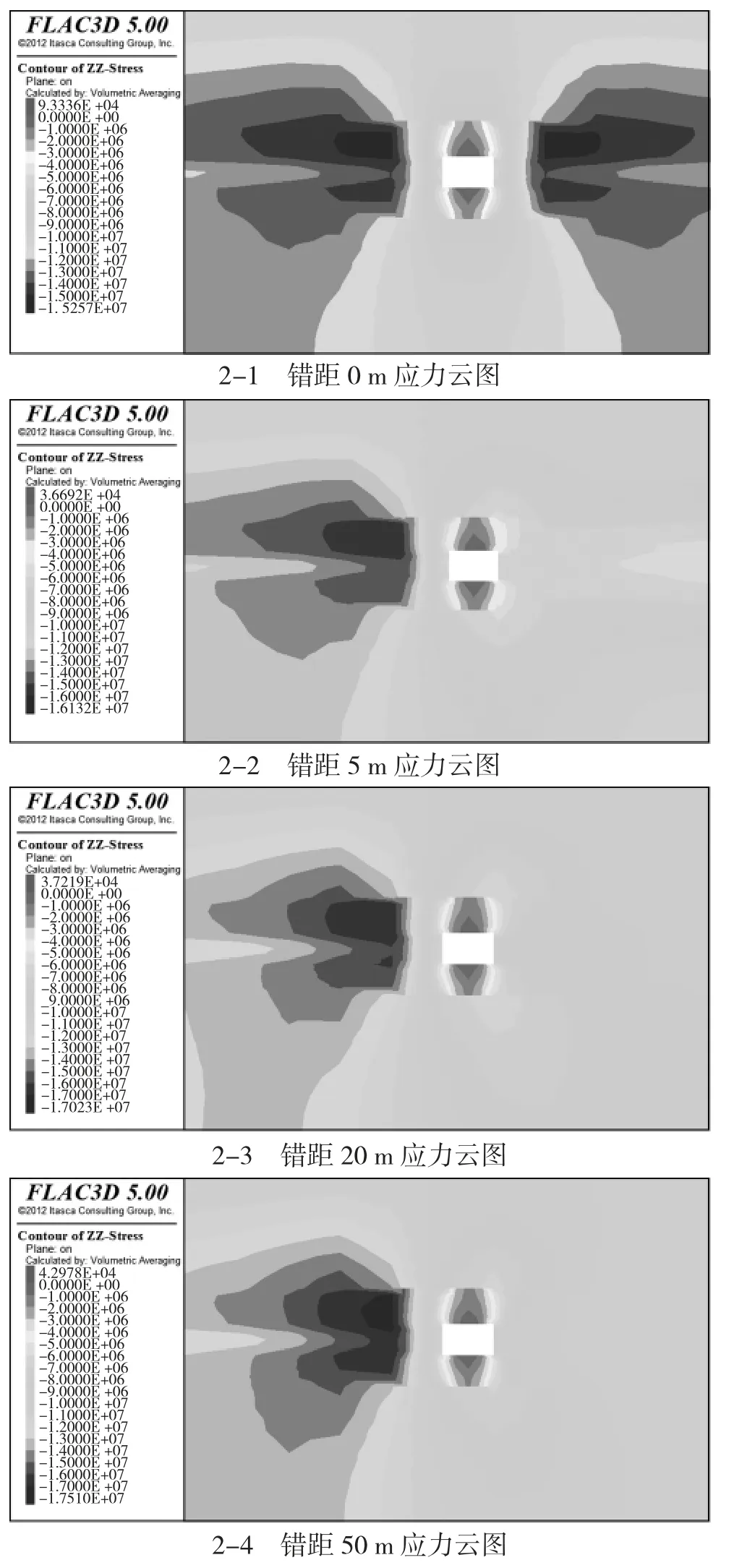
图2 不同错距下中间巷道围岩应力分布云图

从图2 可以看出，当错距为0 m 时，此时巷道顶板及两帮位置出现应力集中，应力大致呈现出对称的趋势，此时的应力峰值为15.3 MPa，当上下工作面有错距且错距为5 m 时，此时在左帮和顶板位置出现应力集中，应力的峰值为16.1 MPa，此时的应力峰值较无错距下增大了0.8 MPa，当上下工作面错距为20 m 时，此时巷道应力集中部位仍为左帮及顶板位置，此时的应力峰值为17 MPa，较无错距应力峰值增大了1.7 MPa，当上下巷道错距为50 m 时，此时的应力集中出现在顶板位置，应力峰值为17.5 MPa，较无错距时应力峰值增大了2.2 MPa。可以看出，随着上下巷道错距的不断增大，巷道的应力峰值逐步增大。这是由于随着上下上到错距的增大，错距段会含有下工作面的超前支撑应力峰值，所以在错距段内压力显现较为剧烈，此时的错距较大使得超前支撑段长度及支护强度都有一定的提升，十分不利用顶板的管理。所以满足机头布置和留巷空间的前提下应当适当降低上下工作面错距，所以最佳的上下工作面错距为5 m[3]。

2 不同充实率下巷道稳定性研究

对工作面错距为5 m 时，对拉充填工作面充实率为50%、60%、70%和90%下的中间巷道围岩变形情况及覆岩运移情况进行研究，模拟云图，如图3 所示。

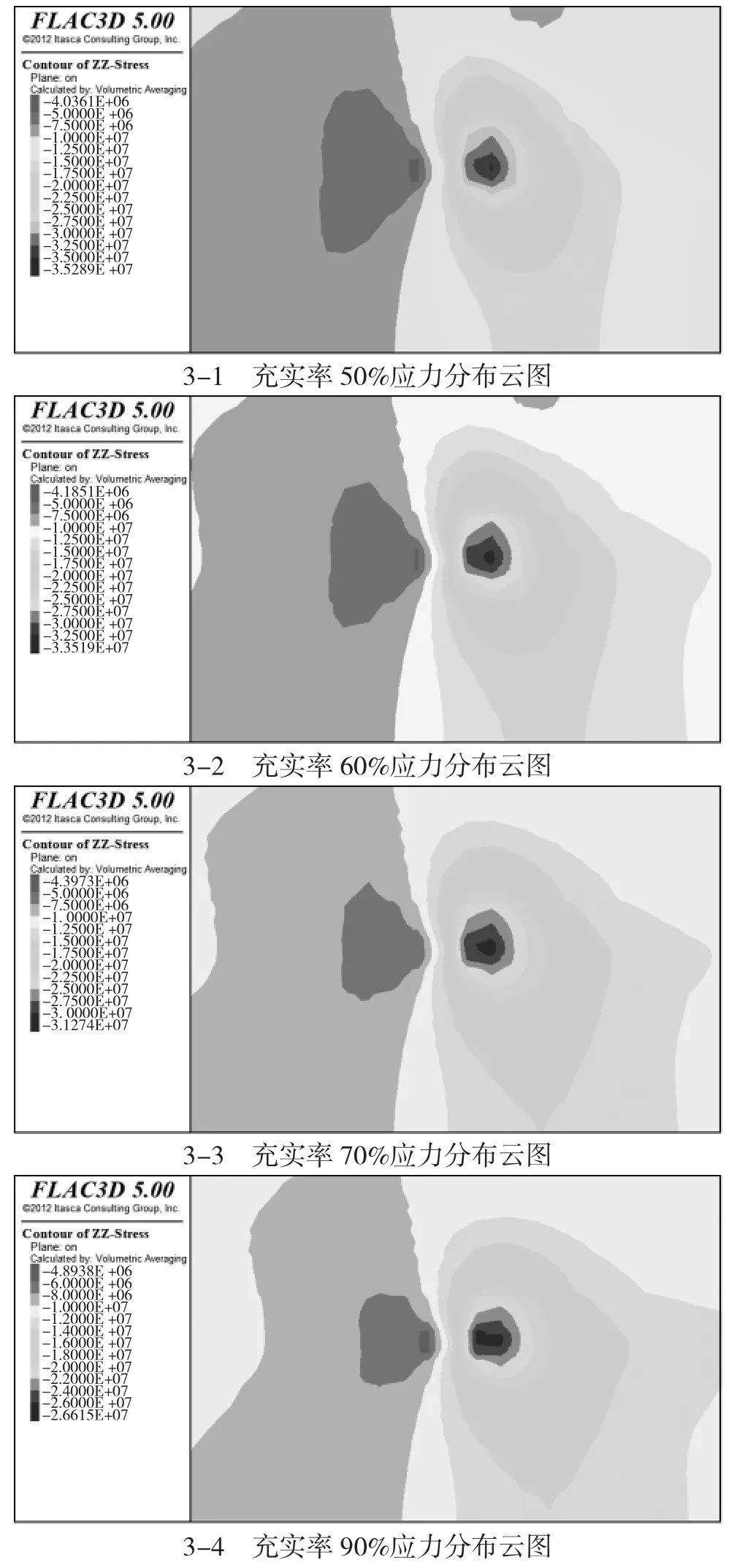
图3 不同充实率下巷道垂直应力分布云图

根据图3 不同充实率下巷道垂直应力分布云图可以看出，在下部工作面的前端位置出现较为明显的应力集中现象，此时的巷道的应力集中极易造成巷道围岩的严重变形，随着充实率的不断增大，巷道应力集中现象逐步降低，巷道的稳定性在逐步提升，巷道的维护成本逐步降低。当充实率为50%时，此时的巷道应力峰值为35.3 MPa，当充实率增大至60%时，此时的巷道围岩的应力峰值为33.5 MPa，应力峰值较充实率50%降低了1.8 MPa，当充实率为70%时，此时巷道围岩的应力峰值为31.2 MPa，应力峰值较充实率50%降低了4.1 MPa，当充实率增大至90%时，此时的巷道的应力峰值降低至26.6 MPa，应力峰值较充实率50%降低了8.7 MPa，可以看出随着充实率的逐步增大，巷道围岩的应力峰值逐步降低，同时使得巷道变形量减小，降低了巷道的维护成本[4]。

对不同充实率下的直接顶下沉量进行研究，直接顶在不同充实率下的下沉曲线，如图4 所示。

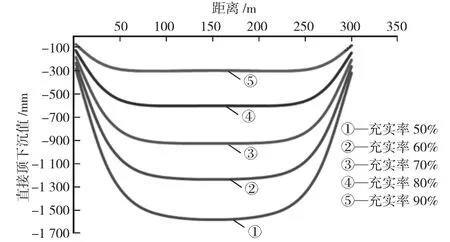
图4 不同充实率下直接顶下沉曲线

可以看出不同充实率下直接顶的下沉量随着距离中间巷道的距离增大呈现出先增大后减小的趋势，在距离为150 m 时取到最大值。随着充实率的增大，直接顶的下沉量逐步增大，当充填率为50%时，此时直接顶的下沉量最大值为1 610 mm，当充填率增大至60%时，此时的直接顶的下沉量最大值为1 200 mm，较充填率50%时减小了410 mm，当充填率增大至90%时，此时的直接顶下沉量最小为300 mm，可以看出随着充填率的增大，巷道直接顶下沉量逐步降低，巷道直接顶的稳定性逐步提升，巷道围岩整体性较好[5]。

3 结论

1）利用数值模拟软件对不同错距下中间巷道围岩应力进行分析发现，随着错距的增大巷道应力峰值逐步增大，巷道稳定性降低，且最佳合理错距5 m。

2）通过对不同充实率下的巷道围岩应力分布情况进行分析，可以看出随着充实率的不断增大，巷道围岩承受的应力最大值逐步降低。

3）通过对不同充实率下巷道直接顶的变形量进行分析发现，随着充填率的增大，巷道直接顶的下沉量逐步降低，巷道稳定性较好。