关于Pell方程组
2022-05-10 00:52何宗友
南宁师范大学学报(自然科学版) 2022年1期
何宗友
(深圳市京田精密科技有限公司,广东 深圳 518118)
设a,b是正整数且不是平方数.求Pell方程组
x2-ay2=1,y2-bz2=1
(1)
的正整数解(x,y,z)是一个基本而重要的数论问题.从Siegel[1]关于超椭圆曲线上整点个数的结果可知,Pell方程组(1)只有有限组正整数解(x,y,z).Baker和Davenport[2]运用Baker关于对数线性型的下界估计,给出了对于给定的a,b求解Pell方程组(1)的方法.本文作者在文献[3]中给出了Pell方程组(1)的正整数解的上界.设N(a,b)表示Pell方程组(1)的正整数解(x,y,z)的个数.近年来,N(a,b)的研究结果如下:
若a,b是正整数且不是平方数,则N(a,b)≤3(Bennet[4]).
若a>3.31×1035,则N(a,b)≤2(袁平之[5]).
若a,b是正整数且不是平方数,则N(a,b)≤2(何波[6]).
若a=4m(m+1),则N(a,b)≤1(袁平之[7]).
若a=4m2-1,则N(a,b)≤1(Mihai Cipu[8]).
若a=2,则N(a,b)≤1(何波,吴文权,杨仕椿[9]).
袁平之在文献[7]中提出如下猜想:
若a,b是正整数且不是平方数,则N(a,b)≤1.
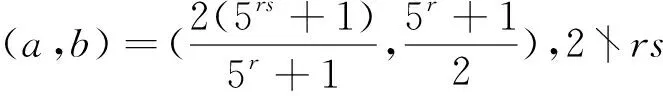
1 定理及其推论
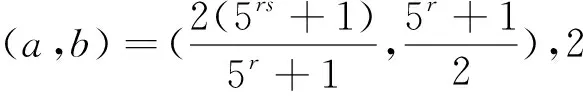
在定理中,取r=1和r=3时,可得到以下两个推论:

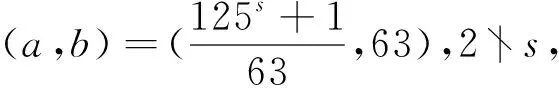

2 定理1的证明
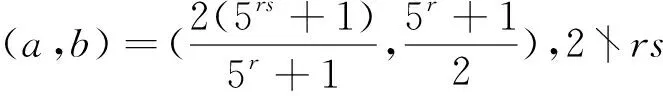
(2)
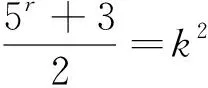
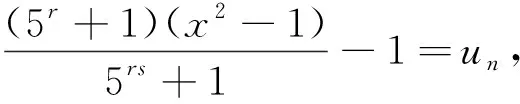
(3)


当n>2时,设n=±2+2·2cl,c≥2,2⫮l,则由文献[10]得um+2·2cl≡(-1)lum(modu2c),故由式(3)得
(4)

故由式(4)得
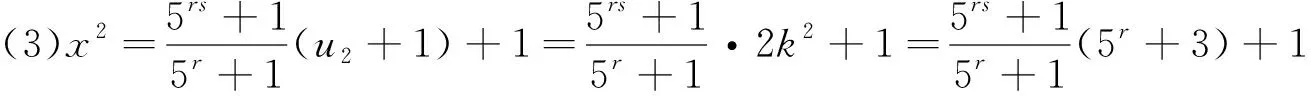
猜你喜欢
中学生数理化·七年级数学人教版(2022年5期)2022-06-05
黑龙江大学自然科学学报(2022年1期)2022-03-29
小学生学习指导(低年级)(2021年9期)2021-10-14
语数外学习·初中版(2020年5期)2020-09-10
中学生数理化·七年级数学人教版(2019年10期)2019-11-25
中等数学(2019年8期)2019-11-25
小学生学习指导(低年级)(2019年9期)2019-09-25
数学物理学报(2019年3期)2019-07-23
小学生学习指导(低年级)(2018年9期)2018-09-26
中学数学研究(广东)(2018年13期)2018-08-11

