《财务管理》教学中一种改进的插值法
■ 东莞理工学院经济与管理学院 谢坤萤 李阳阳 周润书
由王化成、荆新、刘俊彦教授主编、中国人民大学出版社出版的《财务管理学》(第9版)是一本优秀教材。该教材荣获国家级优秀教学成果,并多次入选国家级规划教材。但教材中也存在可以改进的内容,例如,在教材第36~37页的例2~例12中的插值法就可以进行改进。
我们研究原教材中的解题理论,得出该教材中插值法是基于将曲线近似看成线性函数的假设来求解利率的。根据相似三角形的数学原理,提出了下面改进的插值法。
1 原教材内容
现在向银行存入5000元,在利率为多少时,才能保证在今后10年中每年得到750元?
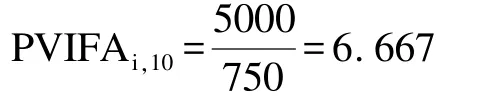
查年金现值系数表,当利率为8%时,系数6.710;当利率为9%时,系数为6.418。所以利率应该在8%~9%之间,假设x为超过8%的利息率,则用插值法计算x的值如下:

原教材解法思路为以下五步:
第一步:根据题意,计算出所求利率i对应的年金现值系数为6.667。
第二步:查年金系数表,得出利率i的年金现值系数6.667介于利率8%的年金现值系数6.710和利率9%的年金现值系数6.148之间,因此确定所求利率i介于8%和9%。
第三步:将9%和8%的年金现值系数进行相减,得出1%利率的变化值。将所求的i和8%的年金现值系数进行相减,得出变化“x%”利率的年金现值系数变化值。
第四步:根据利率变化和年金现值系数变化等比例的关系,计算出“x%”。
第五步:将利率8%加上变化利率x%得出所求利率i。
可以看出:教材的插值法涉及多次算差值的计算,以及最后还需要进行加和才能得出结果,过程繁琐,容易出错,初学者也较难理解各个过程的差值变化。
2 插值法的基本原理
插值法是根据线性函数设置的一种计算方法,虽然货币时间价值计算是非线性函数,但是在求解时,我们可以把两个临界值之间的曲线近似地看成直线。在坐标轴上,x轴表示利率,y轴表示年金现值系数,这样就将求解利率的问题转化为求解函数值的问题。如原教材例题就是将两对已知数据视为两点(8%,6.667)(9%,6.418),确定成一条直线。

图1 原教材插值法原理图
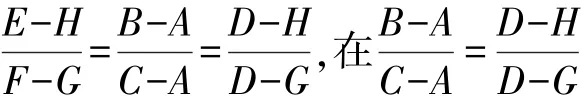

图2 改进插值法原理图
改进的插值法就是将相似三角形的性质融入进运算之中,极大地简化了运算,更好地体现了利率与年金现值系数间的关系,也使整体思路变得更加清晰。
3 改进插值法在原教材例题的应用
现在向银行存入5000元,在利率为多少时,才能保证在今后10年中每年得到750元?
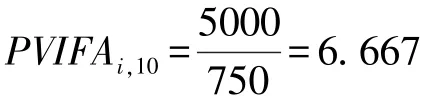
查年金现值系数表,当利率为8%时,系数6.710;当利率为9%时,系数为6.418。所以利率应该在8%~9%之间,假设x为超过8%的利息率,则用插值法计算x的值如下:
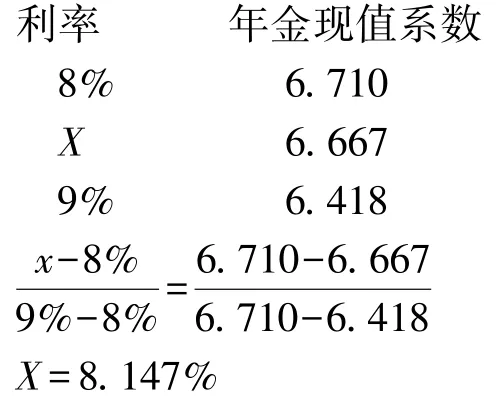
通过对比不难看出,改进的插值法运用相似三角形三边对应成比例的性质,运用等比例的关系,求解出所要求的利率i,不需要像原有插值法一样,先计算利率8%变化到利率i的值x和利率8%变化到9%的值的比率等于年金现值系数6.710变化到6.667的值和6.710变化到6.418的值的比率,然后在利率8%的基础上加上所求的x,最终求出利率i。
改进差值法从未知数上看,所求即为所设,更加方便和易于理解,同时也避免学生在采用原有插值法计算时,算出了变化利率值,却忽略了最终的加和计算。从运算上看,更方便快捷,易于计算。所以,该种方法容易被学生理解和掌握,学生运用这种改进方法时不容易出错。改进插值法的思想与学生已学的初等数学中的相似三角形有着密切的联系,能够让教学达到初学易接受,学完印象深的效果,同时还能做到所学知识运用在新学知识上,让学生感受到知识的乐趣。

