一种SCADE同步语言程序安全属性自动验证工具

孙 毅，陈 哲，冉 丹，杨志斌

1(南京航空航天大学 计算机科学与技术学院，南京211106)

2(华东师范大学 上海市高可信计算重点实验室，上海 200062)

3(南京大学 计算机软件新技术国家重点实验室，南京210093)

1 引 言

反应系统的概念首先由D.Harel和A.Pnueli提出，它不断从环境中得到输入，经过计算后输出给环境[1].同步数据流语言[2，3](简称同步语言)是反应系统最好的开发语言，比如SCADE[4]，Lustre[5，6]和SIGNAL[2]等均为同步语言.航空、航天、核能、交通等安全关键领域的嵌入式系统软件大都是使用同步语言开发的反应系统.形式化验证[7]技术主要包括模型检测和定理证明，模型检测技术[8]是形式化验证技术中一种较为成熟、用于评估信息和通信系统功能特性的重要技术，该技术能准确地检验出给定反应系统的模型是否满足某些属性[9].

随着SCADE同步语言在安全关键领域的应用越来越广泛，使得对SCADE同步语言程序的验证变得至关重要，尤其是SCADE同步语言程序的安全属性.目前，只有工业界存在SCADE同步语言程序的验证工具，即SCADE suite工具，在当前严峻的国际形势下，外部环境倒逼，国内现已不能使用该工具，而我国还不曾突破SCADE同步语言程序形式化验证的“卡脖子”技术.经调研，SCADE同步语言是在Lustre同步语言的基础上发展而来，且SCADE同步语言的语法和语义同Lustre同步语言相似[10]，故可尝试将Lustre同步语言程序的验证技术应用于SCADE同步语言程序中.

目前，国内外对Lustre同步语言程序的形式化验证技术已非常成熟[11-13]，其中，比较先进的形式化验证技术是基于一阶逻辑可满足性的模型检测技术和基于可满足性模理论的求解技术[7]，即首先使用一阶逻辑公式对Lustre同步语言程序的行为进行建模，如此一来，Lustre同步语言程序的安全属性的验证问题便可转化为一阶逻辑公式的可满足性问题；然后使用基于可满足性模理论的求解技术对一阶逻辑公式的可满足性进行求解.

综上，本文提出了一种自动验证SCADE同步语言程序安全属性的方法，旨在实现对SCADE同步语言程序的安全属性进行自动地、直接地验证，以填补SCADE同步语言程序验证领域的技术空白，使得我国对该技术实现自主、可控.本文完成的工作包括：1)从SCADE同步语言程序到无量词一阶逻辑公式的转化(第3节)；2)设计用于验证安全属性的i-归纳求解算法(第4节)；3)构建包括887个SCADE同步语言程序的测试集(第5节)；4)根据所提方法，设计并实现了SCADE模型检测器原型系统工具smc，并通过实验验证了smc工具的有效性，达到了本文的目标(第5节).

2 理论知识

2.1 SCADE同步语言

一个同步语言程序由一个或多个节点(node)构成，每个节点具有零个或更多的输入数据流、局部数据流和一个或更多的输出数据流.同步语言只支持布尔型、整型和实数型数据流，数据流通常用无限序列x1，x2，x3，…)表示，括号内的x1，x2，x3表示这个数据流在第1、2、3个时钟上的值.在同步语言程序中，任何变量和表达式都表示一个由无限个时钟上的值所构成的数据流，例如变量X表示数据流(x1，x2，x3，…).

SCADE同步语言中常用的操作符包括：算术运算符(+，-，*，/，div，mod)、布尔操作符(and，or，not)、关系操作符(>，>=，<，<=)、条件符(if-then-else)、时序操作符.其中，时序操作符主要包括″pre″和″→″，具体如下：

1)″pre″为延迟一个时钟操作符.pre(X)表示将数据流X延迟一个时钟所构成的一个新数据流.例如，如果整型数据流X=(x1，x2，x3，…，xn，…)，那么pre(X)=(nil，x1，x2，…，xn-1，…)，其中nil代表一个未定义的值.

2)″→″为数据流初始化操作符.对于新的数据流″X→Y″，表示使用数据流X在第1个时钟的值初始化该数据流在第1个时钟的值，该数据流在其余时钟的值等于数据流Y在对应时钟的值.例如，如果X=(x1，x2，x3，…，xn，…)和Y=(y1，y2，y3，…，yn，…)是具有相同类型和相同时钟的两个数据流，那么X→Y是与X和Y具有相同类型和相同时钟的数据流，且X→Y=(x1，y2，y3，…，yn，…).

2.2 可满足性模理论

可满足性模理论(Satisfiability Modulo Theories，SMT)应用于很多领域，如软件和硬件验证，类型推理，静态分析等[14]，用于在某个或某些特定背景理论下求解逻辑公式的可满足性问题[15].用以下简单示例来介绍SMT求解器：

P1=(f(r(b，1，m，n+1))≠f(m-n))∧c

其中，P1是需要验证的属性，b为整型数据流，c为布尔数据流，m和n为整型常量数据流，函数r的功能如下：

r(α，ξ，u，v)=if(u=v)thenξelseα

其中，α，ξ为整型数据流，u，v为整型常量数据流.函数f的规则是：当参数相同时，其函数值便相等.此处的例子是无效(invalid)的，设n=m-1，则得到P1=(f(r(b，1，m，m-1+1))≠f(m-m+1))∧c，化简得P1=(f(1)≠f(1))∧c，得到属性P1不成立.

本文使用的SMT求解器为Z3求解器[16]，它是一款由微软开发的先进的开源工具.

2.3 有界模型检测

有界模型检测(Bounded Model Checking，BMC)[17，18]的思想很简单，即通过穷举的方式判断所有的系统状态是否都满足逻辑公式.具体做法是通过逐步增加内存深度来检测系统状态是否满足逻辑公式，直到发现某系统状态不满足逻辑公式或者内存深度超出设置的阈值为止.它的检测方法是通过验证如下公式是否成立：

N(1)∧N(2)∧…∧N(i)→P(1)∧P(2)∧…∧P(i)

N(i)由SCADE同步语言程序在第i个时钟的等式集合Δ(i)(见第3.3节)使用合取运算符相连得到，P(i)表示第i时钟需要验证的安全属性的逻辑公式.整型数据流i从1开始，如果公式成立则增加i的值后继续判断公式是否成立，直到公式不成立返回反例或者i的值超过预设阈值.

3 SCADE程序到无量词一阶逻辑公式的转化

本节的工作是将SCADE同步语言程序及安全属性转化为无量词一阶逻辑公式.下面的SCADE同步语言程序实现了一个速度调节器，可以通过按up和down按钮进行速度调节，该程序将作为例子贯穿全文，代码如表1所示.

表1 SCADE同步语言程序例子Table 1 A example of SCADE program

在Ctr节点中，速度阈值margin设置为10.5，速度目标值target的初始值为60.0.该节点中的速度目标值target可以通过按up/down按钮进行调节：如果down按钮被按下，速度目标值减1.0；如果up按钮被按下，速度目标值加1.0；否则速度目标值保持不变.最后通过调用Adj节点计算代表减速和加速控制指令的输出数据流decelerate和accelerate.在Adj节点中将实际速度actual与速度目标值target进行对比，如果二者的差值大于阈值margin则进行减速(decelerate为true)，小于阈值-margin则进行加速(accelerate为true).

转化过程包括：1)将程序中的枚举值、用户定义类型和常量内联到节点中(第3.1节)；2)将被调用节点全部内联到主节点中(第3.2节)；3)降低程序的内存深度(第3.3节)；4)提取无量词一阶逻辑公式(第3.4节).

3.1 内联变量

我们引入映射数据结构(即一个键值对集合)来实现本小节的内联工作，其中枚举值、用户定义类型和常量的键值对分别表示为、和.其中，enum_value_id表示枚举值标识符，enum_value表示与枚举值标识符对应的整数值，user_type_id表示用户定义类型标识符，type表示与用户定义类型标识符对应的类型，constant_id表示常量数据流标识符，constant_value表示与常量数据流标识符对应的常量值.构建好映射数据结构后，通过遍历SCADE同步语言程序，将映射数据结构中的键在程序中的所有出现替换为其在映射中对应的值.

具体操作见算法1，该算法的输入为SCADE同步语言程序p1，输出为不包含枚举值、用户定义类型和常量的SCADE同步语言程序p2.算法首先构建3个键值对集合(2-4行)，其复杂度是O(n)；然后将键值对集合中的键在程序中的所有出现替换为其在集合中对应的值(5-17行)，其复杂度也是O(n)；所以该内联变量算法的复杂度为O(n).

算法1.内联变量算法

输入：SCADE同步语言程序p1

输出：无枚举、用户类型和常量的SCADE同步语言程序p2

1.begin

2.构建键值对集合enum_values

3.构建键值对集合user_types

4.构建键值对集合constants

5.for数据流标识符ieinp1

6.ifie是键值对集合enum_values中的键

7.then用键ie在enum_values中的值替换ie

8.endif

9.ifie是键值对集合constants中的键

10.then用键ie在constant中的值替换ie

11.endif

12.endfor

13.for数据流定义vdinp1

14.ifvd是键值对集合user_types中的键

15.then用键vd在user_types中的值替换vd的类型type

16.endif

17.endfor

18.返回内联操作后得到的SCADE同步语言程序p2

19.end

下面举例说明.假设SCADE同步语言程序中的一个枚举类型定义为type color=enum {red，green，blue}，其中type为枚举类型定义的关键字，color为该枚举类型的标识符，red、green和blue为枚举值的标识符.本小节使用一个映射数据结构存储枚举值的键值对，此处存储的内容为{，，}.假设SCADE同步语言程序中存在一个整型数据流y1，并且有等式y1=green.通过遍历该SCADE同步语言程序，将这个等式替换为y1=1.

3.2 内联节点

假设SCADE同步语言程序中主节点的主体为N=A∪{y=t[f(a)]}，其中f(a)是对程序中另一个非主节点f的调用，节点调用的参数为a，t[f(a)]是包含节点调用f(a)的表达式，y=t[f(a)]是一个等式，A表示主节点中不包含节点调用的其他等式集合.假设被调用节点f中的等式集合为B，输入流集合为I，输出流集合为O，局部流集合为L.本节主要反复执行以下两个步骤：标识符重命名和内联被调用节点中的等式.具体操作见算法2，该算法的输入为算法1的输出程序p2，输出为只包含单一节点的SCADE同步语言程序p3.该算法利用一个全局队列queue来存储所有可能包含节点调用表达式的等式，算法直至队列queue中为空为止.算法2中的前缀格式中的“nodename”为被调用节点的标识符，整数i≥0表示第i+1次调用和内联该节点.该内联节点算法的复杂度为O(kn)，即O(n).

算法2.内联节点算法

输入：SCADE同步语言程序p2

输出：包含单一节点的SCADE同步语言程序p3

1.begin

2.构造p2的节点表node_table并获取p2的主节点main

3.将主节点main中的所有等式插入全局队列queue中

4.删除主节点中所有的等式

5.whilequeue.empty()do

6. e=queue.front()；

7.if等式e的右边不是节点调用表达式

8.then直接将等式e插入全局容器result中

9.elseif等式e的右边是节点调用表达式

10. 构造唯一前缀“nodename～i～”

11. 从节点表node_table中获取该被调用节点nd

12. 利用唯一前缀给节点nd所有数据流重命名，并将重命名后的数据流存入全局容器new_locals中

13. 构造内联前节点nd中数据流标识符和重命名后的数据流的映射表trans

14. 利用trans构建重命名后节点nd中的输入数据流与等式e右边节点调用的实参之间的等式集合，并插入到queue中

15. 利用trans将节点nd中的所有等式中的数据流标识符替换为重命名后的数据流标识符，并将所有等式插入queue中

16.endif

17. queue.pop()；

18.done

19.将容器result中所有的等式插入主节点main的等式集合中

20.将容器new_locals中的所有数据流加入主节点main局部数据流locals中作为主节点main的局部数据流

21.返回只有由main一个节点组成的SCADE同步语言程序p3

22.end

以下假设节点f标识符重命名后的等式集合为B′，输入流集合为I′，输出流集合为O′，局部流集合为L′.

算法2中将标识符重命名后的被调用节点内联进主节点N=A∪{y=t[f(a)]}，得到新的节点N=A∪{y=t[f(a)/O′]}∪{I′=a}∪B′，其中t[f(a)/O′]表示在表达式t中用O′代替f(a)，{I′=a}是由被调用节点f中的输入流集合I′和参数a对应组成的等式集合，同时将被调用节点f中的数据流I′、O′、L′全部作为主节点N中的局部流.

在本例中，主节点Ctr调用节点Adj，且只有一次调用，对Adj节点的输入流、输出流和局部流的标识符进行重命名，得到的输入流为：Adj～0～actual、Adj～0～target、Adj～0～margin，输出流为：Adj～0～decelerate、Adj～0～accelerate.内联节点操作完成后得到的SCADE同步语言程序如表2所示.

表2 转化得到的单一节点SCADE同步语言程序Table 2 Converted single node SCADE program

3.3 降低内存深度

通过引入新的局部数据流将程序的内存深度降为1(如果大于1)，即使得任何数据流在当前时钟的值都只依赖于数据流在当前时钟或前一个时钟的值.引入的局部数据流的标识符的格式为″～flatten～i″，其中i从0开始递增.经过3.2节的内联操作后得到一个包含单一节点N的SCADE同步语言程序，以下假设N中的数据流集合为V={x1，x2，…，xp，y1，y2，…，yq}，其中x1～xp是输入数据流，y1～yq是局部或输出数据流.由N中的数据流y1～yq在第i个时钟上的值y1(i)～yq(i)构成的等式集合Δ(i)表示为：

其中，V(i)表示V中的数据流在第i个时钟上的值，t1～tq是表达式，这些表达式可能包含V(i)～V(i-d)中的元素作为子表达式，d是N中″pre″操作符的最大内存深度，即任何数据流在当前时钟的值都只依赖于数据流在过去d个时钟以内的值.降低内存深度的具体操作见算法3，该算法的输入为算法2的输出程序p3，输出为内存深度不大于1且大于等于0的SCADE同步语言程序p4.该算法的复杂的分两种情况：若程序p3的内存深度不大于1，则复杂度为O(n)；若程序p3的内存深度大于1，则复杂度为O(n2).

算法3.降低内存深度算法

输入：SCADE同步语言程序p3

输出：内存深度d小于等于1的SCADE同步语言程序p4

1.begin

2.设置一个全局静态变量i且初始值设为0

3.for二元表达式beinp3

4.if二元表达式be的等号右边的表达式ue为一元表达式

5.then

6.whileue的操作符为pre且操作数含有时序操作符do

7. 构建新数据流“flatten～i”并插入全局容器new_local

8. 利用原二元表达式be等号左边等于“pre(～flatten～i)”构成新的二元表达式并插入全局容器new_equations中

9. 将原二元表达式be从程序p3中删除

10. 用一元表达式ue的操作数替换一元表达式ue

11.i：=i+ 1；

12.done

13.endif

14.endfor

15.返回操作后得到的SCADE同步语言程序p4

16.end

假设数据流yi和数据流xj之间存在一个包含d个″pre″操作符的等式yi=pre(pre(…(pre(xj))))，则引入d-1个新的局部数据流～flatten～0，～flatten～1，…，～flatten～d-2，删除原来的等式，并增加等式yi=pre(～flatten～0)，～flatten～0=pre(～flatten～1)，…，～flatten～d-2=pre(xj)，使得等式中″pre″操作符的最大内存深度由d降低为1.经过本小节的转化，节点N的等式集合变为如下形式：

其中yq+1～ym是新增的局部数据流，tq+1～tm是表达式.我们将节点N中的数据流在第i个时钟上的值V(i)称为瞬时结构，例如Δ(i)中的y1(i)～ym(i)的值就是由第i和i-1个时钟上的瞬时结构构成的等式，因此可以说明节点N就是基于瞬时结构的约束型系统[7].

3.4 提取逻辑公式

将算法3的输出程序p4及其安全属性P表示为在第i个时钟上的无量词一阶逻辑公式N(i)和P(i)，其中N(i)是将Δ(i)(见3.3节)中的等式集合用合取运算符相连得到，P(i)是将P中的数据流标识符用该数据流在第i个时钟上的值替换后得到的表达式.

在本例中，SCADE同步语言程序在第i个时钟上的无量词一阶逻辑公式表示如下：

N(i)：=(m(i)=10.5)∧

(t(i)=ite(i=1，60.0，ite(d(i)，t(i-1)-1.0，ite(u(i)，t(i-1)+1.0，t(i-1)))))∧

(dr(i)=adr(i))∧(ar(i)=aar(i))∧

(aa(i)=a(i))∧(at(i)=t(i))∧(am(i)=m(i))∧

(adr(i)=(aa(i)-at(i))>am(i))∧

(aar(i)=(aa(i)-at(i))<-am(i))

其中，m，t，d，u，dr，ar，a，adr，aar，aa，at，am依次表示margin，target，down，up，decelerate，accelerate，actual，Adj～0～decelerate，Adj～0～accelerate，Adj～0～actual，Adj～0～target，Adj～0～margin，m(i)表示数据流m在时钟i上的值，其他类似，ite表示if-then-else函数.

其次，设待验证的安全属性为“此速度调节器会一直发出减速控制指令”，即P：=(dr=true)∧(ar=false)一直成立.因此，安全属性在第i个时钟上的命题逻辑公式表示如下：

P(i)：=(dr(i)=true)∧(ar(i)=false)

4 验证安全属性

将SCADE同步语言程序转化为无量词一阶逻辑公式后，我们利用SMT求解器验证转化得到的无量词一阶逻辑公式是否满足表示待验证安全属性的无量词一阶逻辑公式.主要包括两个步骤：构造两个验证公式和证明这两个公式是否成立.我们构造的两个公式为：

N(0)∧N(1)∧…∧N(i)→P(0)∧P(1)∧…∧P(i)

(1)

N(n)∧…∧N(n+i+1)∧P(n)∧…∧P(n+i)→P(n+i+1)

(2)

n表示一个值不确定的整数，i是任意的自然数，因为我们转化后的SCADE同步语言程序的内存深度可能等于1，所以i需要从0开始才能完整表达第1个时钟(i=1)的完整瞬时结构.我们使用这两个公式结合有界模型检测和归纳法[19]的思想设计了算法4，即i-归纳求解算法.

算法4的输入为算法3的输出程序p4，输出分两种情况：如果安全属性有效则输出″valid″，无效则输出反例.该算法中分配了两个相互独立的公式集合β和γ，分别用于存放公式(1)和公式(2).函数add_bmc_fml(φ)和函数add_ind_fml(φ)的功能是将公式φ分别加入到公式集合β和γ中；函数verify_bmc(ρ)和函数verify_ind(ρ)的功能分别是验证公式集合β和γ中现有的公式能否推导出公式ρ，如果能推出公式ρ则返回true，如果不能则返回false；函数get_cex()用于返回一组能推导出公式ρ的取值，该组取值即为能推导出公式ρ的反例.对于该算法的复杂度，因其涉及一阶逻辑可满足性判定问题，故其为NPC问题[20].

算法4.i-归纳算法

输入：标有待验证安全属性的单一节点SCADE同步语言程序p4

输出：安全属性有效返回valid，无效则返回反例

1.begin

2.add_bmc_fml(N(0)∧N(1))；

3.ifverify_bmc(P(0)∧P(1))

4.thenreturnget_cex()；

5.endif

6.add_ind_fml(N(n)∧N(n+1)∧N(n+2)∧P(n)∧P(n+1))；

7.ifverify_ind(P(n+2))

8.thenreturnvalid；

9.endif

10.i：=1；

11.whiletruedo

12.i：=i+1；

13.add_bmc_fml(N(i))；

14.ifverify_bmc(P(i))

15.thenreturnget_cex()；

16.endif

17.add_ind_fml(N(n+i+1)∧P(n+i))；

18.ifverify_ind(P(n+i+1))

19.thenreturnvalid；

20.endif

21.done

对于i的某个取值，若公式(1)不成立，则说明程序在第i个时钟上不满足安全属性，并且可以从使得公式N(0)∧N(1)∧…∧N(i)∧(P(0)∧P(1)∧…∧P(i))成立的取值中产生一条反例路径.如果对于i的某个取值公式(1)和公式(2)都成立，则说明安全属性是程序满足的不变式，即该安全属性是有效的；如果公式(1)成立而公式(2)不成立，则说明无法在当前i值下证明安全属性是不变式，因此接下来逐步增加i的值，并再次尝试证明两个验证公式是否成立.

在本例中，公式(1)是不成立的：注意dr(i)=adr(i)=(aa(i)-at(i))>am(i)，假设在i=1时的实际速度a(1)=70.0，代入数值后得到dr(1)=(70.0-60.0)>10.5，因此dr(1)=false.即此速度调节器不会一直发出减速控制指令，也就是说P(1)=false，所以此性质P不是不变式.

5 实验与分析

在Linux环境下，我们使用C++语言开发实现了原型系统工具smc.smc工具能够准确有效的验证SCADE同步语言程序的安全属性，且smc工具具有较高的验证效率，经实验统计发现，在包含887个SCADE同步语言程序的SCADE测试集中，90.08%的程序可在90秒内被smc工具验证完毕，87.51%的程序可在30秒内被验证完毕，58.66%的程序可在3秒内被验证完毕.

考虑到目前尚不存在针对SCADE同步语言程序的形式化验证工具，也不存在SCADE同步语言程序测试集，为了验证smc工具的有效性，我们做了如下工作：首先，我们构建了一个包含887个SCADE同步语言程序(分为6个文件夹)的测试集，本文称之为SCADE测试集，该SCADE测试集是通过将Lustre标准测试集(1)Lustre标准测试集获取地址为https：//github.com/kind2-mc/kind2-benchmarks[11]利用SCADE suite工具(国内现已不能使用)建模而来，与Lustre标准测试集的功能等价.然后，我们使用JKind[12]工具(一款非常先进的、针对Lustre同步语言程序的、使用JAVA语言开发的模型检测器)作为评价原型系统smc是否有效的参考，即使用等价的SCADE测试集和Lustre标准测试集分别作为smc工具和JKind工具的测试集，以此来验证原型系统工具smc能否准确有效的验证SCADE同步语言程序的安全属性.

本次实验的统计结果分为两种：第1种是验证结果为有效(valid)的运行时间；第2种是验证结果为无效(invalid)的运行时间.因为计算机资源(主要是内存)的限制，我们设置了一个运行时间限制(90秒)，导致还有一种验证结果为超时(timeout)，我们没有对超时的验证结果做统计，因为不同配置的计算机会导致不同的超时结果，所以该结果是没有意义的.本次实验的机器配置为32G内存，双核CPU，实验使用Ubuntu16.0.4的64位Linux操作系统，gcc 5.4.0编译器.

表3和表4中，第1列均为文件夹名(两个测试集中等价的两个程序的文件名及其所在的文件夹名均相同)；第2列分别为文件夹中验证结果为有效(表3)和无效(表4)的同步语言程序的个数；第3列是原型系统工具smc验证SCADE测试集的结果分别为有效(表3)和无效(表4)的运行时间；第4列是JKind工具验证Lustre标准测试集的结果分别为有效(表3)和无效(表4)的运行时间.表3的运行时间保留整数部分，表4的运行时间保留一位小数，时间单位均为秒(s).

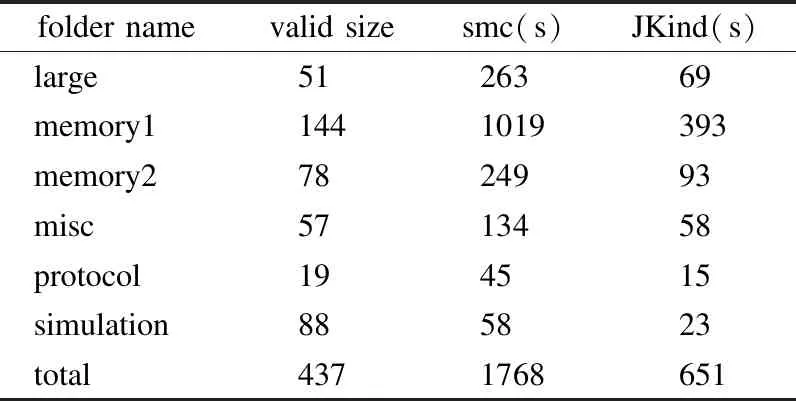
表3 结果为有效的运行时间Table 3 Time of valid results

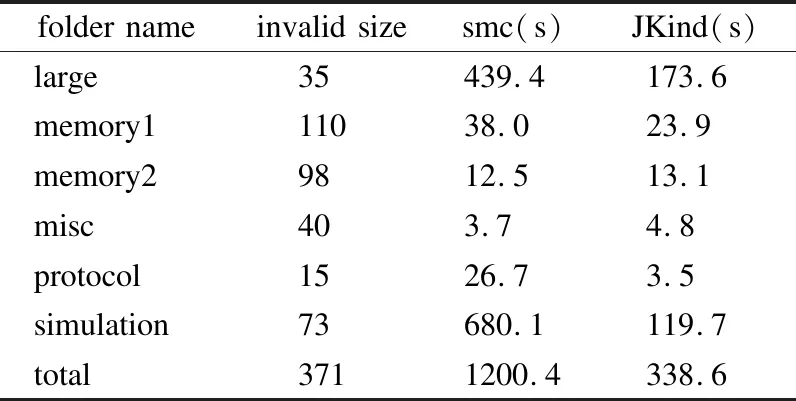
表4 结果为无效的运行时间Table 4 Time of invalid results

图1是由表3和表4绘制而成的散点图，图中的每个圆圈代表两个测试集中两个等价的程序，其横坐标为使用smc工具验证SCADE测试集的运行时间，纵坐标为使用JKind工具验证Lustre标准测试集的运行时间，时间单位为秒(s).

图1 smc对比JKind散点图Fig.1 smc vs JKind scatter plot

观察表3和表4可知，对于两个等价的测试集，smc工具和JKind工具得出的验证结果分别为有效和无效的程序数量均是一样的，即887个程序中，smc工具和JKind工具验证结果为有效的数量均为437个，验证结果为无效的数量均为371个，剩下的79个均为超时.此外，我们进一步通过分析实验数据发现：对两个测试集中的任意两个等价的程序，分别使用smc工具和JKind工具验证得到的验证结果是一致的.这说明，原型系统工具smc能够准确地验证SCADE同步语言程序中的安全属性是否有效，即验证了本文提出的方法是有效的.而且，通过本次实验的过程证明了原型系统工具smc完成了能够对SCADE同步语言程序进行自动地、直接地验证的目标.

为了进一步探讨smc工具的验证效率，我们绘制了图1.可以从表3、表4和图1中看出，smc工具的验证效率不及JKind工具，这是因为JKind工具实现了包括路径压缩和抽象技术等多种优化方法，而本文的原型系统工具smc只实现了有界模型检测和归纳法，暂未实现这些优化方法.但是，smc工具是目前除SCADE suite工具外唯一能够验证SCADE同步语言程序安全属性的模型检测器，使得我国在SCADE同步语言程序安全属性的形式化验证领域实现自主可控.

6 结束语

本文提出了一种自动验证SCADE同步语言程序安全属性的方法，填补了SCADE同步语言程序验证领域的技术空白；根据所提方法，本文开发实现了原型系统工具smc，并通过实验验证了该工具能够准确有效的对SCADE同步语言程序的安全属性进行自动地、直接地验证；在未来的工作中，我们会引入运行时验证[21]等方法来提高smc工具的验证效率.