孤岛交流微电网鲁棒自适应H∞补偿控制*

王 君 张园芳，2

（1.兰州理工大学电气工程与信息工程学院 兰州 730050）（2.甘肃省工业过程先进控制重点实验室 兰州 730050）

1 引言

孤岛模式下，微电网系统须在微电源具有相对稳定的电压和频率，并使它处在一个可控范围内，才可稳定运行［1］。分布式电源具有一定的间歇性和随机性，利用储能装置可维持系统的正常运行。随着新能源发电控制技术的不断演进，电网系统的故障率也在不断增大。研究发现，逆变器是造成微电网控制系统故障率高的重要因素之一［2～4］，通过容错控制设计使逆变器安全可靠的运行已经受到了一定的关注。文献［12］考虑系统存在不确定性及外界干扰，提出一种基于高阶滑膜观测器的连续积分滑膜容错控制方法。文献［13］考虑系统存在不确定，外部干扰及非脆弱，结合LMI设计了一种鲁棒H∞稳定控制器，实现了多种因素干扰下系统仍能稳定运行。文献［15］针对多电平逆变器，提出在不改变系统拓扑图下，构建贝叶斯网络对逆变器开关元件进行故障诊断，重构变载波和调制波电压。上述文献主要采用的是基于数据驱动的方法，利用FDD子系统估计故障，需要提供精确及时的故障信息且出现误诊故障的可能性较大。一类无需FDD子系统，在线直接重构控制器实时补偿执行器故障对系统造成的影响，可以快速地达到容错效果。因此，根据实时的故障特征，在线设计自适应容错控制律的方法是十分必要的。

因此，本文针对不确定孤岛交流微电网系统，考虑执行器故障及外部存在有限能量扰动时，提出鲁棒自适应H∞补偿控制器的设计方法。首先，建立不确定孤岛交流微电网系统的故障模型；其次，在执行器发生故障时，在线调节控制器的参数，补偿执行器故障和参数摄动对系统造成的影响。最后，仿真验证了所提方法的有效性。

2 问题描述

2.1 孤岛交流微电网主电路拓扑

孤岛交流微电网系统拓扑如图1所示［3］，包括直流输入电压源Udc、6个全控型功率器件IGBT、电能传输线路上的电阻、开关器件上的微小电阻和LCL低通滤波器。Udc表示微电网中的微电源；每相IGBT器件的等效串联电阻、逆变器输出到微电网交流母线的低压等效电阻和LCL滤波器阻尼电阻分别为R1、R2和R。

图1 孤岛交流微电网拓扑图

2.2 孤岛交流微电网系统故障模型

假设系统是在理想状态下稳定运行，考虑传输线路上的电能损耗和开关损耗，建立孤岛系统的数学模型。由基尔霍夫电压电流定律，并采用Clarke变换可得到孤岛交流微电网LCL型逆变器连续的三阶数学模型［6］。

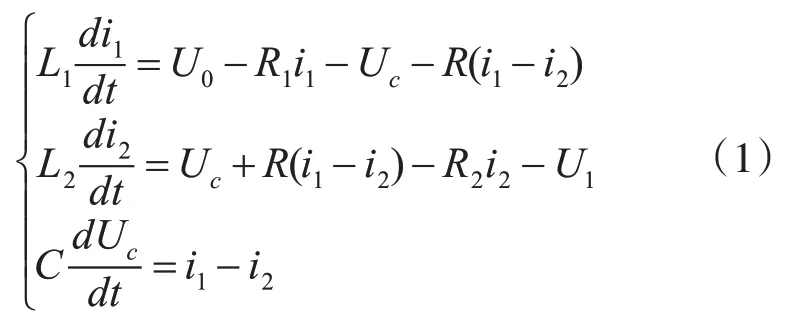
式中，i1表示电感L1的输出电流；i2表示电感L2的输出电流；U0表示逆变器输出电压；Uc为电容C端电压；U1表示储能装置输出电压。

定义x(t)=[i1，i2，Uc]T，从而得到系统的状态空间表达式：

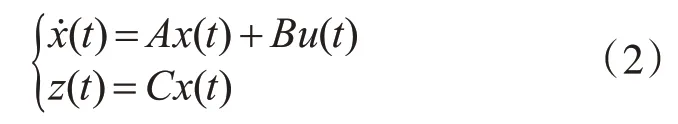
式中，x(t)∈Rn为系统状态变量，u(t)∈Rm为控制输入，u(t)=[U0，U1]T；z(t)∈Rp为测量输出。

在实际电力系统中，系统内部和外部均存在一些不确定因素，本文将内部不确定性因素假定是由电感L1引起的参数摄动，执行器故障是由分布式电源逆变器和储能装置逆变器引起。综合上述因素，系统的实际数学模型为

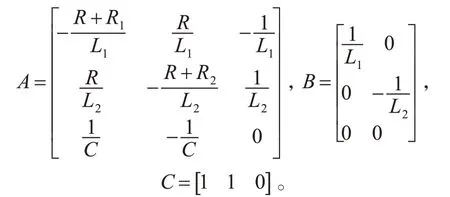
一般情况，执行器故障情形包括中断、卡死、部分失效和偏移故障，定义执行器故障形式为［11］

其中，ρ=diag(ρi)，ρi∈(0，1)；σ=diag(σi)，σi∈(0，1)；us(t)表示未知时变有界卡死/偏移故障。

带有执行器故障的孤岛交流微电网动态系统故障模型为

为了使设计的控制器具有更好的容错能力，给出如下假设［9］。

假设1系统的所有状态可测，且对所有执行器故障情形ρ，{A，Bρ}系统完全可控。

假设2非参数卡死故障和外部扰动为分段连续有界方程，即存在未知常数和，使得

假设3对孤岛交流微电网动态系统故障模型（式（5）），存在一个有恰当维数的矩阵F使得方程B1=BF成立。

假设4所有执行器故障情形ρ满足rank(Bρ)=rank(B)，且根据实际情况执行器发生故障时不能自动返回到正常状态，即ρ˙(t)≤0。

由假设1可知，{A，B}是稳定的，则存在一个常数矩阵K和正定矩阵P使得

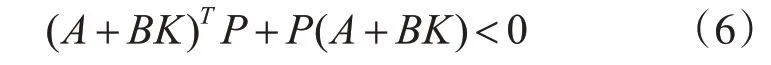
而假设4保证了B列的线性组合可被Bρ中的列重构，即存在一个K0满足

由式（6）和式（7），存在一个常数η→∞时，使得

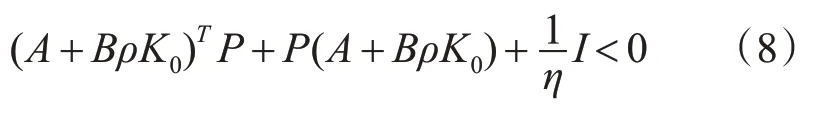
本文采用直接自适应容错控制方法构造自适应状态反馈控制器u(t)，使得受扰故障系统（式（5））一致稳定且具有一定的扰动抑制能力。

2.3 自适应H∞容错控制器设计

直接自适应容错控制器采用如下形式：

式中，K0保证系统的稳定性；K1(t)补偿系统参数摄动和执行器故障给系统带来的影响。

将式（9）代入式（5）可得孤岛交流微电网闭环故障系统：

2.4 相关引理及定义

3 主要结果

考虑执行器故障，当存在外部扰动时，实现自适应容错控制的设计目标是寻求自适应H∞控制增益矩阵K0，在线调节自适应律k^1和k^2补偿执行器故障和系统参数摄动对系统造成的影响，使得不确定孤岛交流微电网闭环故障系统（式（10））满足下列条件：

1）闭环故障系统（式（10））一致稳定；

2）零初始条件下，闭环故障系统（式（10））具有一定的扰动抑制性能。

定理给定常数η，如果存在矩阵X=XT＞0和具有适当维数矩阵W，满足如下线性矩阵不等式

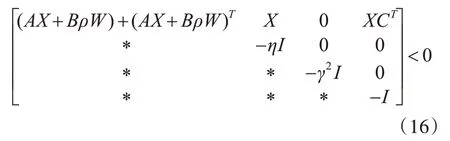
则存在自适应状态反馈控制律（式（9）），使闭环故障系统一致稳定，且对于任意执行器效率因子ρ具有一定的扰动抑制性能。固定控制增益矩阵K0=W X-1、变控制增益矩阵K1(t)由自适应控制律实时调节。

证明构造Lyapunov函数如下，

由定义1可知，闭环系统有次优H∞性能。证明完毕。

4 仿真算例

系统的初始条件为x(0)=[1 0 10 220]T，考虑系统可能发生的模式：

1）正常模式1。分布式电源逆变器和储能装置逆变器均正常运行，即ρ11=ρ12=1。

2）故障模式2。储能装置逆变器正常运行，分布式电源逆变器分别发生部分失效和卡死故障，描述为ρ22=1，a1≤ρ21≤1和ρ21=0，其中a1=0.4表示为分布式电源逆变器最大的失效率。

在仿真中，考虑故障模式2，在10s之前，微电网系统正常运行，10s之后分布式电源逆变器发生部分失效，效率因子为ρ2=1-0.03t直至失效率为40%，20s之后，发生卡死故障时，us=10+sint。选取n(t)=0.5e-t，自适应律的初始条件为仿真效果图如下。图2和图3分别为在初始条件x(0)=[1 0 10 220]T下，当执行器发生不同类型的故障模式时，得到零输入状态响应曲线；图4表示自适应控制器参数ki(t)(i=1，2)的估计曲线。

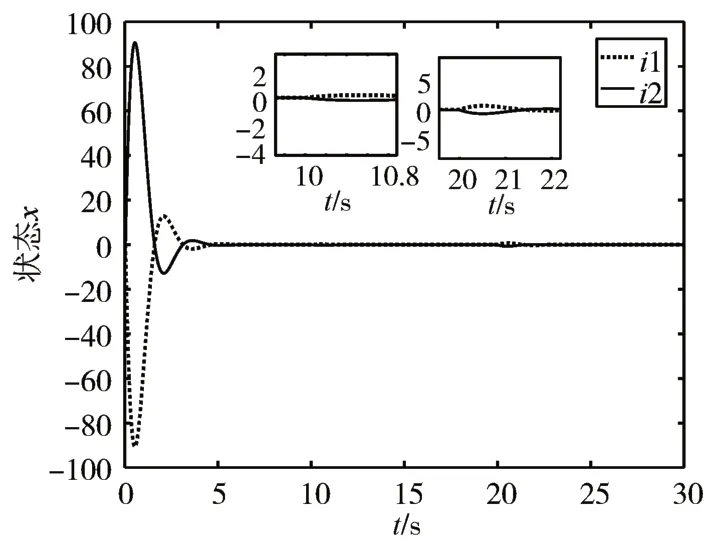
图2 零输入状态ik(k=1，2)响应曲线

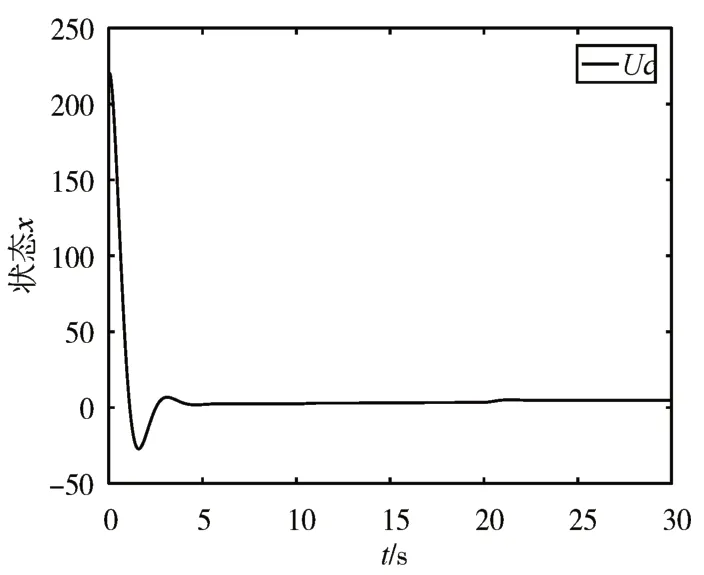
图3 零输入状态Uc响应曲线

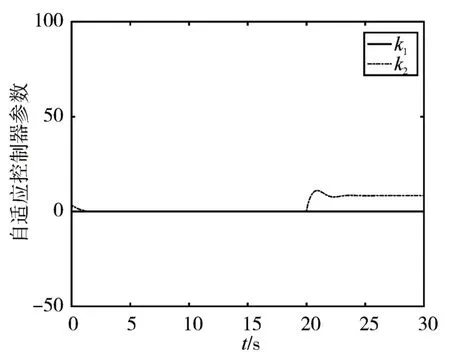
图4 控制器参数ki(i=1，2)估计响应曲线

从图2和图3可以看出，10s之前，系统稳定运行；10s之后系统的执行器发生部分失效，所设计的自适应控制器仍能使系统在执行器发生故障的情形下，经过一段时间趋于稳定；20s之后执行器发生卡死故障时系统仍然稳定运行，由此可看出被控对象的三个状态都达到了良好的控制效果。从图4可以看出，在系统执行器发生故障时，控制器参数ki(t)(i=1，2)的估计曲线最终收敛于某一常值，表明控制输入信号有界，系统稳定运行。可知本文提出的自适应补偿方法能有效地控制自适应控制器参数的变化轨迹，ki(t)(i=1，2)的估计曲线一致有界。

5 结语

针对孤岛交流微电网系统，考虑执行器部分失效和卡死故障模式，采用自适应补偿方法，研究了受扰不确定孤岛交流微电网系统H∞容错控制问题。本文建立了存在外部扰动的不确定孤岛交流微电网系统的闭环故障模型之后；首先，在执行器正常和已知故障模式下，离线设计具有更小保守性的H∞容错控制器，用来保证系统的稳定性；然后利用自适应方法，设计直接自适应补偿控制律，实时补偿执行器发生的未知故障对系统带来的影响，确保孤岛交流微电网故障系统一致稳定且具有一定的扰动抑制性能。最后，仿真结果表明，采用自适应补偿方法不仅能确保系统在发生执行器故障时一致稳定，而且使系统具有一定的抗干扰能力，验证了所提方法的有效性。