基于Kriging模型的高速列车齿轮箱箱体裂纹识别*

王靖铭 宁 静 赵 飞 陈春俊

（西南交通大学机械工程学院 成都 610031）

1 引言

高速列车作为一种高度集成的复杂系统［1］，各部件故障会对其运行安全性产生不同程度的影响。齿轮箱作为高速列车走行部的关键部件，是保证高速列车正常运行的A类关键部件，其主要作用是传递扭矩、改变速度和扭矩方向［2］。其结构损伤既影响列车运行速度，同时也影响列车转向架结构性能，严重时可能引发列车事故［3］。箱体裂纹作为齿轮箱系统的常见损伤，严重影响列车运行安全性。因箱体裂纹而造成列车事故的情况在国内外均有出现。自2012年国内某型号动车组首次出现齿轮箱箱体疲劳裂纹以来，截至目前，已累计发生疲劳失效百余起［4］。因此，如何进行箱体裂纹的有效判断和识别，对保证列车安全运行具有重要的研究意义。

近年来，随着人们对于计算机技术和统计学的深入研究和应用，代理模型技术被广泛应用于各个领域。在代理模型方法研究方面，目前已发展了包括Kriging模型、神经网络、径向基函数等多种代理模型方法。其中，Kriging模型首次提出是在1951年南非地质学家Krige的硕士论文中，作为一种无偏估计模型被用来估计方差最小化［5］。20年后，此方法于1971年被Matheron首次命名为Kriging方法［6］。Cressie在总结Kriging技术研究的基础上，详细阐述了其原理［7］。随后，Currin等［8］和Sacks等［9］将Kriging方法应用到实际工程问题的优化中。至此，Kriging方法开始正式步入工程领域，至今已发展为最具代表性和应用潜力的代理模型方法之一［10］。

随着Kriging代理模型技术被广泛应用于工程领域，部分学者开始将其应用到结构裂纹识别领域，并取得不错的效果。高海洋等提出了一种基于Kriging代理模型的裂纹识别方法，结果表明，该方法能有效地识别裂纹参数，与基于有限元的方法相比，极大地提高了识别效率，并且具有良好的抗噪性［11］。鲁志文将Kriging代理模型用于运行状态下转子裂纹参数的量化识别，结果表明，与基于BP神经网络的方法相比，在保证裂纹位置和深度识别的准确性的情况下，该方法需要的样本量更少，且对噪声鲁棒性较强［12］。王丹阳基于Kriging代理模型，结合改进的NSGA-Ⅲ实现了在转子运行状态下识别裂纹的位置、深度和类型［13］。

由上可知，虽然Kriging代理模型技术的应用已经开始涉及到裂纹识别领域，但相比于工程领域的其他方面，可谓微不足道。且大多局限于简单结构（如梁、板以及转子等）裂纹识别研究。针对于此，本文开展基于Kriging代理模型的非运行条件下高速列车齿轮箱箱体裂纹识别研究。通过少量的箱体裂纹损伤样本与其结构响应，直接构造裂纹参数与其结构响应间对应关系的Kriging代理模型，在保证识别精度与效率的情况下实现箱体裂纹识别。

2 Kriging代理模型技术

Kriging模型作为一种半参数化的插值技术，由多项式和随机分布两部分组成，故可表示为如下数学形式：

其中，β是回归系数；f(x)是x的多项式，用于设计空间中提供全局近似模拟；z(x)为随机分布的误差，模拟局部误差近似，具有以下统计特性：

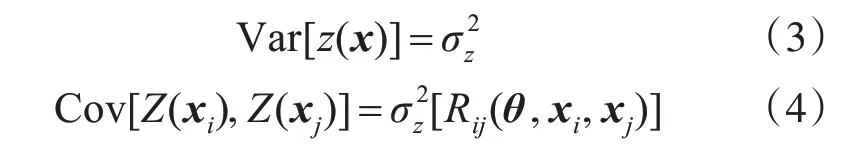
式中，xi、xj是训练样本中任意两点；R(θ，xi，xj)是带有参数θ的相关函数，用于表征训练样本点间的空间相关性。

对于给定训练样本集S=[x1，x2，…，xn]及其响应集Y=[y1，y2，…，yn]，在式（1）给定的模型基础上，可通过已知训练样本响应值Y的线性组合来估计任意一个待测点xnew的响应值，即：

此式即可表征待测点与各样本点间的空间相关性。

上式中的差值系数c可通过最小化响应预测值的预测方差来确定，即

由上可知，只需求得参数β、θ以及即可。可通过最大化响应值的似然估计来计算：

3 基于Kriging模型的裂纹识别步骤

裂纹识别问题本质上可转化为优化问题，即在所建立的Kriging代理模型基础上，利用寻优算法确定满足目标函数的裂纹参数，从而实现裂纹识别。假设已测得结构响应y(x*)，则目标函数可表示为

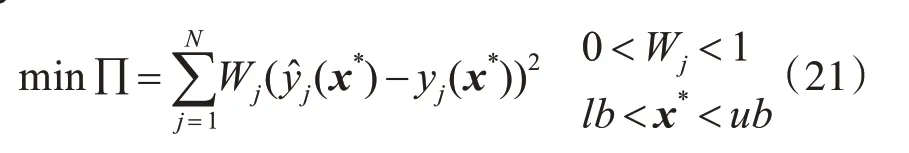
式中，Wj为加权参数；为测试点x*在模型中所对应的预测响应的第j个分量；lb和ub为裂纹无量纲参数的上限和下限，N为y^(x*)的长度。

如图1所示，基于Kriging代理模型的裂纹识别步骤可总结如下。

图1 基于Kriging代理模型的裂纹识别步骤

1）根据裂纹结构特性，确定可描述裂纹位置和大小的参数作为设计变量，从而构建设计空间。

2）利用合适的抽样方法抽样生成裂纹参数初始样本点，本文采用拉丁超立方体抽样。利用有限元仿真得到样本点所对应的结构响应。

3）基于初始样本点及其响应值构建Kriging模型，在所构建的代理模型基础上使用寻优算法进行寻优识别。

4）基于寻优识别结果验证Kriging代理模型的计算精度，若满足精度要求，则输出识别结果。

5）若不满足精度要求，则需进行Kriging代理模型修正，即将识别结果作为样本点加入初始样本集重构样本集，从新构建Kriging代理模型。

6）重复上述步骤3），直到满足精度要求。

4 基于Kriging模型的箱体裂纹识别

4.1 基于模态分析的箱体裂纹参数抽样

模态是机械结构固有的振动特性，每阶模态都有特定的固有频率、阻尼比和模态振型［14］。通过模态分析可了解结构系统的振动特性，为结构故障诊断和预防以及结构动力特性优化设计提供依据。本文通过对箱体进行模态分析可了解到箱体结构本身的固有属性，从而掌握箱体结构易损部位，为后续箱体裂纹参数抽样提供参考。

由于箱体结构形状复杂，为了便于有限元分析，因此在建立箱体模型时，不考虑上下箱体结合部、轴承端盖与箱体结合部的影响，忽略箱体局部尺寸较小或者影响甚微的部位，如箱体的泄油孔、螺栓孔等［15］。本文借助Pro/E建立箱体三维模型，并将之导入ABAQUS中进行箱体模态分析。箱体材料采用铸造铝合金，材料密度为2.7×103kg/m3，弹性模量为75Gpa，泊松比为0.3。经模态分析计算，箱体前六阶模态振型和频率分别如图2和表1所示。

图2 齿轮箱箱体前六阶振型

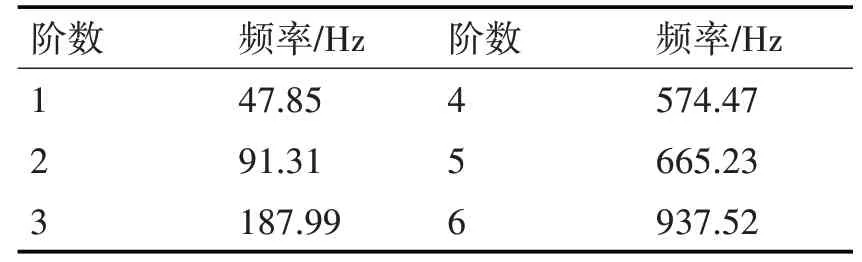
表1 齿轮箱箱体前六阶固有频率

从箱体前6阶模态频率可以看出，箱体的固有频率多集中在高频阶段，应力集中多发生在窥油孔周围和箱体底座以及端部。结合箱体实际产生裂纹实例如图3所示，选取箱体底座和端部为研究对象。假设箱体表面有一裂纹，裂纹平面与轴心位于同一平面上，且假设裂纹纵向深度不超过箱体壁厚，裂尖位置径向上不超出输出轴轴孔，以裂纹在轴心圆所在的方位（角度）θ、径向宽度α以及轴向深度β为裂纹参数，构建一个具有三维变量的设计空间，则有θ∈[240，360]、α∈[0，30]、θ∈[0，12]。利用拉丁超立方抽样抽取裂纹参数样本如表2所示。

图3 齿轮箱箱体裂纹实例

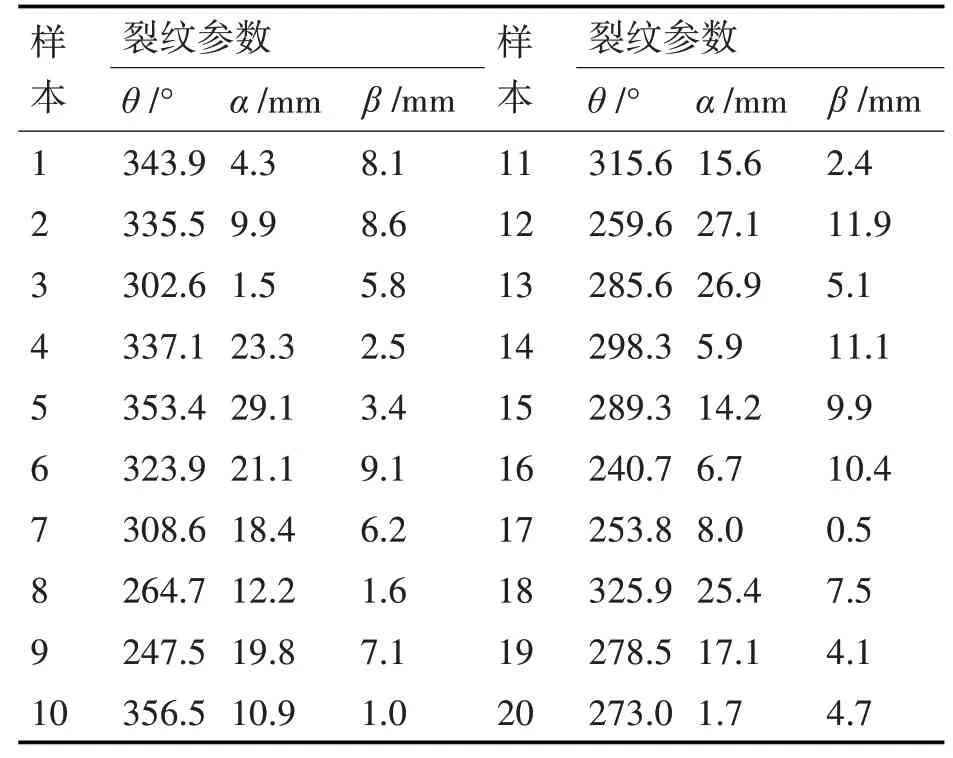
表2 齿轮箱箱体裂纹参数样本

4.2 基于ABAQUS的裂纹箱体结构响应提取

结合前文抽取的裂纹参数样本，利用ABAQUS进行箱体裂纹建模，基于建立的裂纹箱体模型进行模态分析，从而提取所对应的结构响应。约束边界条件如下：箱体与C型支架连接平面为固定约束，大轴承孔处采用耦合约束，约束除绕车轴旋转自由度以外的其他自由度［16］。本文采用云图积分定制箱体裂纹，图4为样本点12的箱体裂纹模型。图5示为12号样本点箱体裂纹模型的第13阶模态振型图，从图中可以看出所定制裂纹的位置出现明显的箱体裂纹，这也证明了所建立的裂纹模型的准确性。

图4 样本点12箱体裂纹模型

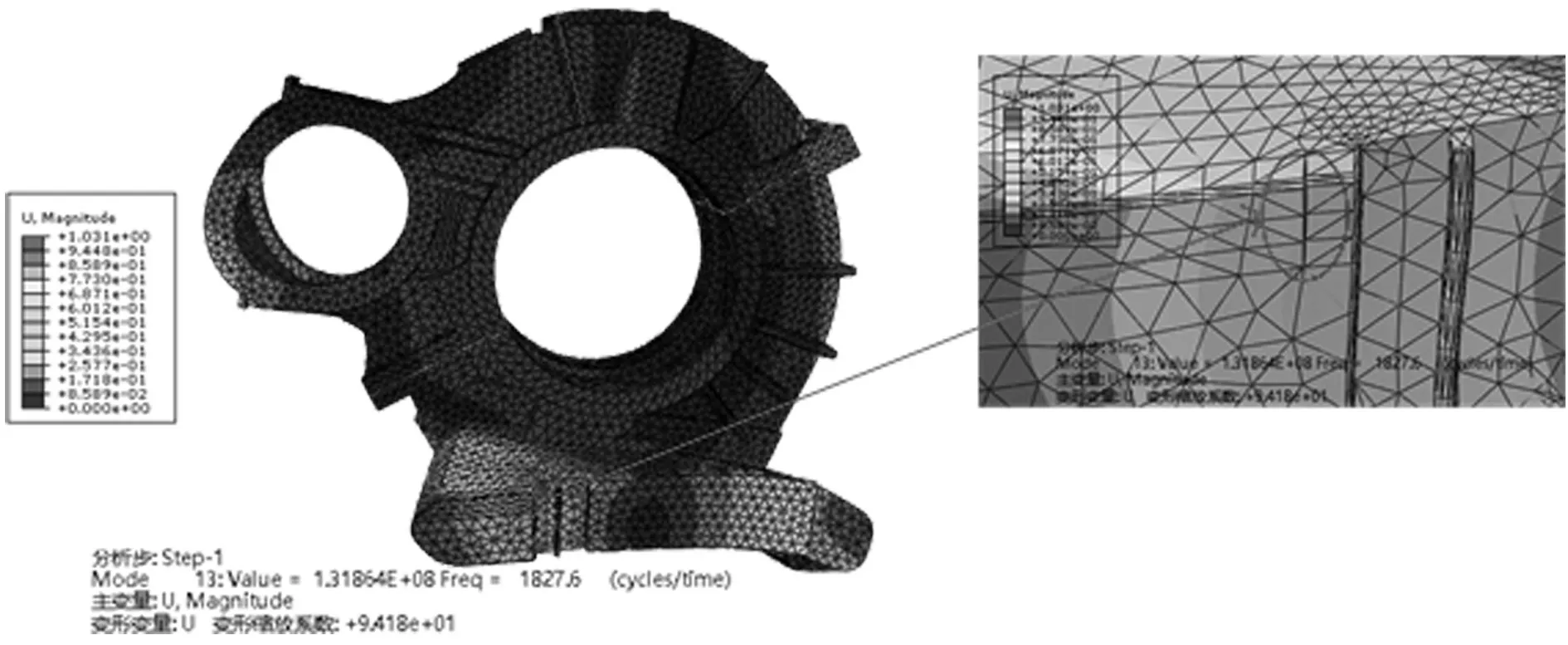
图5 12号样本点箱体裂纹模型第13阶模态振型

根据表2所抽取20组裂纹参数样本点，并利用ABAQUS建立对应箱体裂纹模型，通过模态分析提取裂纹参数样本点所对应的模态频率。为保证结构响应对裂纹参数的变化相对灵敏，同时确保计算效率，通过对比分析，本文选取各裂纹参数样本点所对应的12阶、14阶、16阶和18阶固有频率作为裂纹参数所对应的结构响应，见表3。

4.3 Kriging代理模型构建与箱体裂纹识别

根据表3的裂纹参数样本以及其对应的结构响应构建Kriging代理模型。结合箱体模态分析与箱体裂纹实例，在箱体模型上利用ABAQUS软件模拟四种裂纹工况，进行Kriging代理模型精度验证，验证结果如表4所示。由表4可以看出，四种工况下各裂纹参数的识别精度均低于工程误差限值5%。

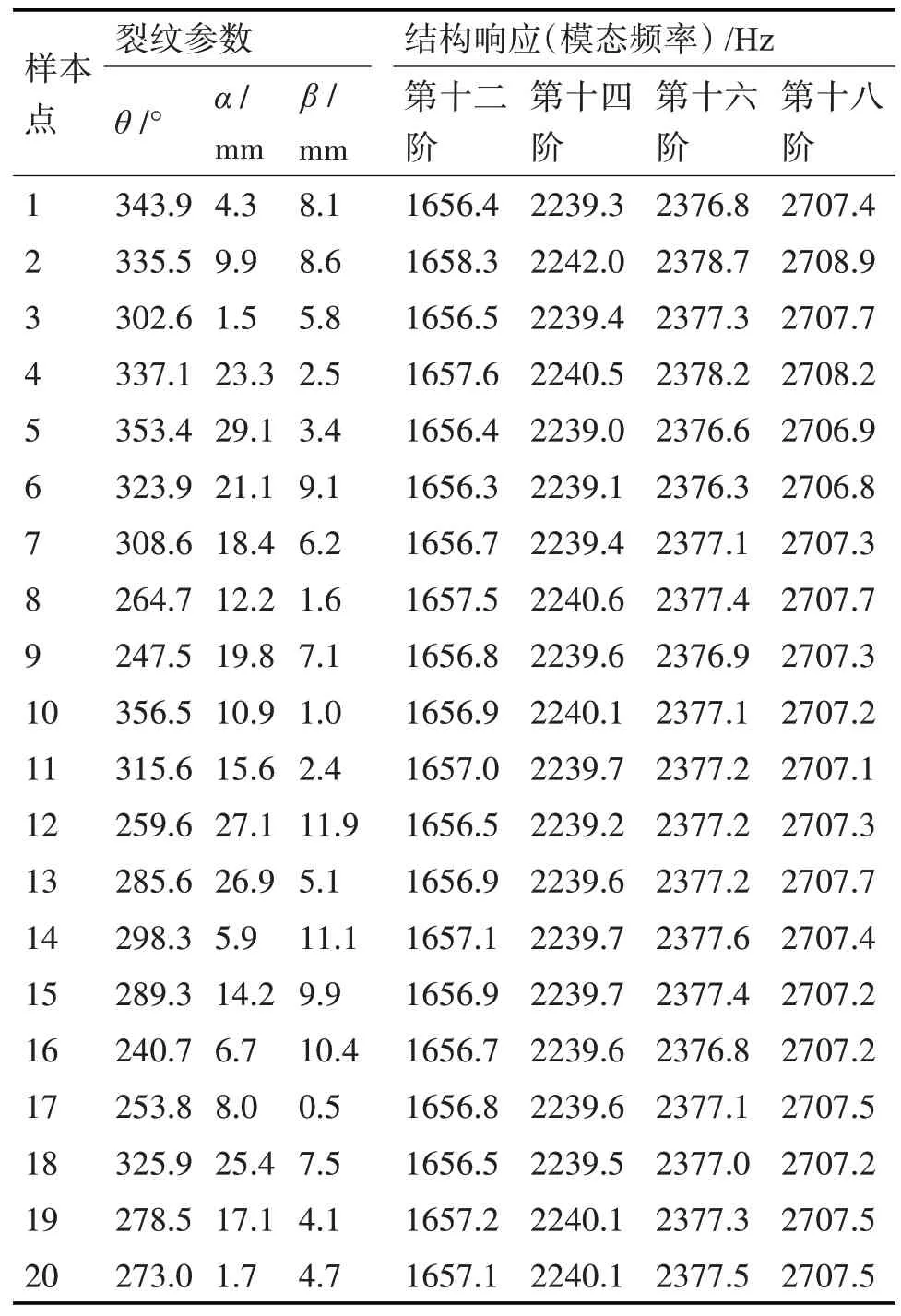
表3 各裂纹参数样本及其所对应的结构响应

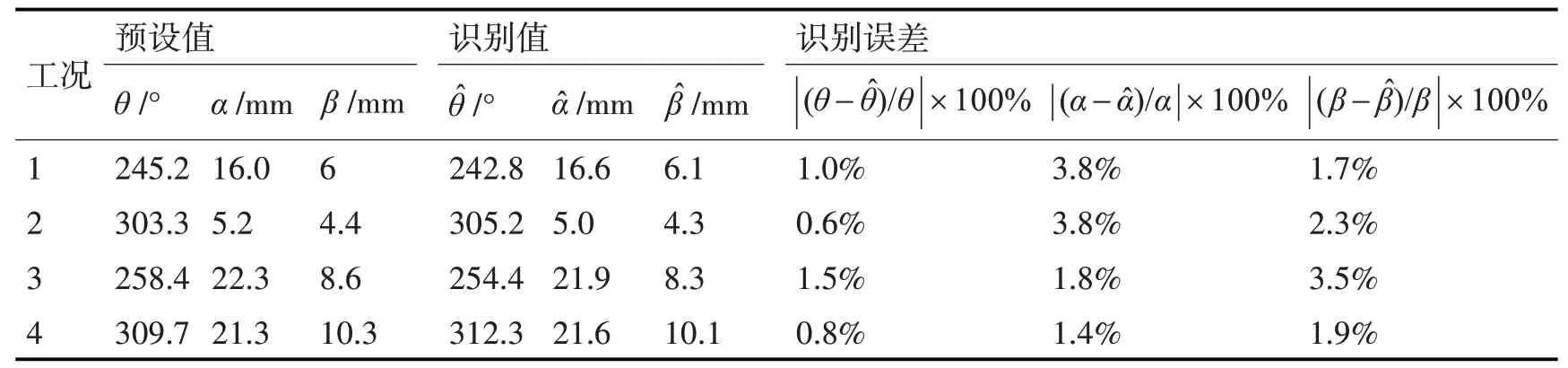
表4 模拟的四种工况裂纹参数与识别结果对比

其中，表示裂纹轴心圆方位的参数θ识别精度最高，其识别误差均低于2%。此外，虽然表示裂纹径向宽度的参数α以及轴向深度的参数β识别精度相对偏低，但其识别误差也均低于4%。这说明所构建的Kriging代理模型满足精度要求，无需通过加点准则进行模型修正。同时，通过裂纹识别结果可以看出，率为结构响应之间的关系具有明显的优势，其仅需在建模以及模型验证时调用少量有限元计算（本文共调用24次），就可得到能代表无数次有限元分析计算裂纹识别模型。在保证裂纹识别精度的条件下，大大减少了计算成本，提高了裂纹识别的效率。

5 结语

随着我国高铁事业的飞速发展，高速列车的相关研究也因此蓬勃发展。然而，目前对高速列车齿轮箱箱体裂纹识别研究却微乎其微。此外，近年来虽然有学者将Kriging代理模型应用于裂纹识别领域，但基本上都局限于板、梁等简单结构。基于以上情形，本文针对某型高速列车齿轮箱箱体发生裂纹故障从而影响列车运行的安全性问题，结合当下应用广泛且最具应用潜力的Kriging代理模型，初步探析了非运行条件下高速列车齿轮箱箱体的裂纹识别。主要结论如下：

1）利用结构发生损伤时结构的固有属性发生变化这一特性，利用有限元分析软件ABAQUS建立箱体的裂纹模型，并基于模态分析得到裂纹箱体的各阶固有频率，从中选出四阶联合作为裂纹箱体结构响应，从而构建Kriging代理模型，实现非运行条件下箱体裂纹识别，并通过模拟四种工况验证了模型的准确性。

2）根据识别结果表明，与基于信号处理和基于数值分析的裂纹识别相比，该方法在保证识别精度的情况下，极大地提高了识别效率，同时还可实现微小裂纹识别以及裂纹定位识别。