基于位置一步预测的核相关目标跟踪算法①

石昌森,侯 巍,杨琳琳,杨诗博

1(河南大学 人工智能学院,开封 475001)

2(河南大学 计算机与信息工程学院,开封 475001)

1 引言

视频目标跟踪是指对图像序列中机动目标进行检测、提取、识别和跟踪,以获得机动目标位置、速度、加速度、运动轨迹等运动参数,从而对机动目标进行进一步处理与分析的过程[1].随着计算机运算能力和存储能力的迅速发展及大数据分析需求的逐渐增大,视频跟踪技术在交通控制[2]、视频检索[3]、人机交互[4]等方面有了广泛应用.早期的目标跟踪算法主要根据目标建模或对目标特征进行跟踪,主要的方法有基于目标模型建模方法与基于搜索的方法[1].特征匹配法是常用的基于目标模型建模方法,首先提取目标特征,然后在后续帧中找到最相似的特征进行目标定位;均值漂移(mean-shift)算法[5]是常用的基于搜索的方法,该方法利用图像特征构造概率密度函数,由梯度方向搜索局部最大值作为目标位置.由于在新近的较有挑战的数据集例如VOT2018 或者大规模数据集TrackingNet上,传统跟踪算法达不到实际要求,而深度学习因为其强大的特征提取能力以及端对端的训练模式慢慢受到了广泛关注.近年来越来越多基于深度学习的跟踪方法被相关学者提出,Chao 等[6]将深度学习网络及自适用相关滤波器结合,提出了ECO(efficient convolution operators for tracking)算法,该算法在速度和精度上都有较好的表现.Wang 等[7]使用Transformer[8]深度学习跟踪器将不同时刻视频帧桥连起来,传递了丰富的时序信息,该算法在最新数据集上有很高的速度与精度.

在对视频中目标跟踪过程中不可避免会存在目标快速移动问题,即对视频序列中机动目标进行跟踪时,如果跟踪目标在前后两视频帧间位移超过20 个像素点,则被认为是快速移动[9].此时目标可能超出了搜索范围或移动到了搜索范围边界,导致丢失目标的情况,进而跟踪失败.目标位置预测是解决机动目标快速移动问题的首要难点,虽然卡尔曼滤波算法可以快速预测目标位置,但是不能很好地解决机动目标运动过程中存在的非线性情况,而粒子滤波算法具有解决非线性问题的特性,对非线性运动过程有较好的预测效果.Nummiaro 等[10]提出了基于颜色特征的粒子滤波跟踪(particle filter,PF)算法.PF 首先在目标区域提取颜色特征,然后散播粒子,计算每个粒子的权重,最后根据粒子位置及权重预测目标位置.PF 提取目标区域颜色特征,得到丰富的特征信息,可以有效地对非刚性和快速移动目标进行跟踪,而且在遮挡以及复杂环境情况下也有较好的鲁棒性.然后对目标位置进行修正,为了正确跟踪目标,修正算法需要有较高的速率及准确率,深度学习方法准确率高但运行时间过长.Bolme 等[11]设计了MOSSE(minimum output of squared error )滤波器,将计算由时域转换到频域,提供了运算速度,对信号相关性的求解保证了算法精度.MOSSE 虽然运算速度快,但不能直接对快速移动的机动目标进行跟踪.Henriques 等[12]在MOSSE 基础上引入循环矩阵及核函数,提出CSK(circulant structure of tracking-bydetection with kernels)算法.精度上相对于MOSSE 有了很大提升,但CSK 特征选取比较单一,而且对快速移动情况没有处理,很难直接跟踪快速移动的机动目标.Henriques 等[13]在CSK 的基础上改变灰度特征提取为FHOG 特征提取,同时加入核方法,提出了KCF(kernel correlation filter)及DCF(dual correlation filter)算法,KCF 对应非线性核,DCF 对应线性核.Li 等[14]在KCF 的基础上将单一特征选择扩展为多个特征选择,并添加了尺度池,提出了SAMF(scale adaptive with multiple features tracker)算法.SAMF 算法虽然精度相对于KCF 有些许提升但是速度比较慢,所以这里选择KCF 作为修正算法.最后针对机动目标在视频中由于快速移动问题导致的形变、模糊问题,融入零截距以及平均峰值相关能量.实验结果表明,新方法在公开数据集OTB100 与UA-DETRAC 上都有较高的识别率.

2 核相关滤波

3 粒子滤波

4 基于位置一步预测的核相关目标跟踪算法

式中,k表示一个大于1 的常数,M00/256表示搜索框中属于目标的像素点个数[25],目标框的长度为 ηs( η为目标框长宽比例系数).

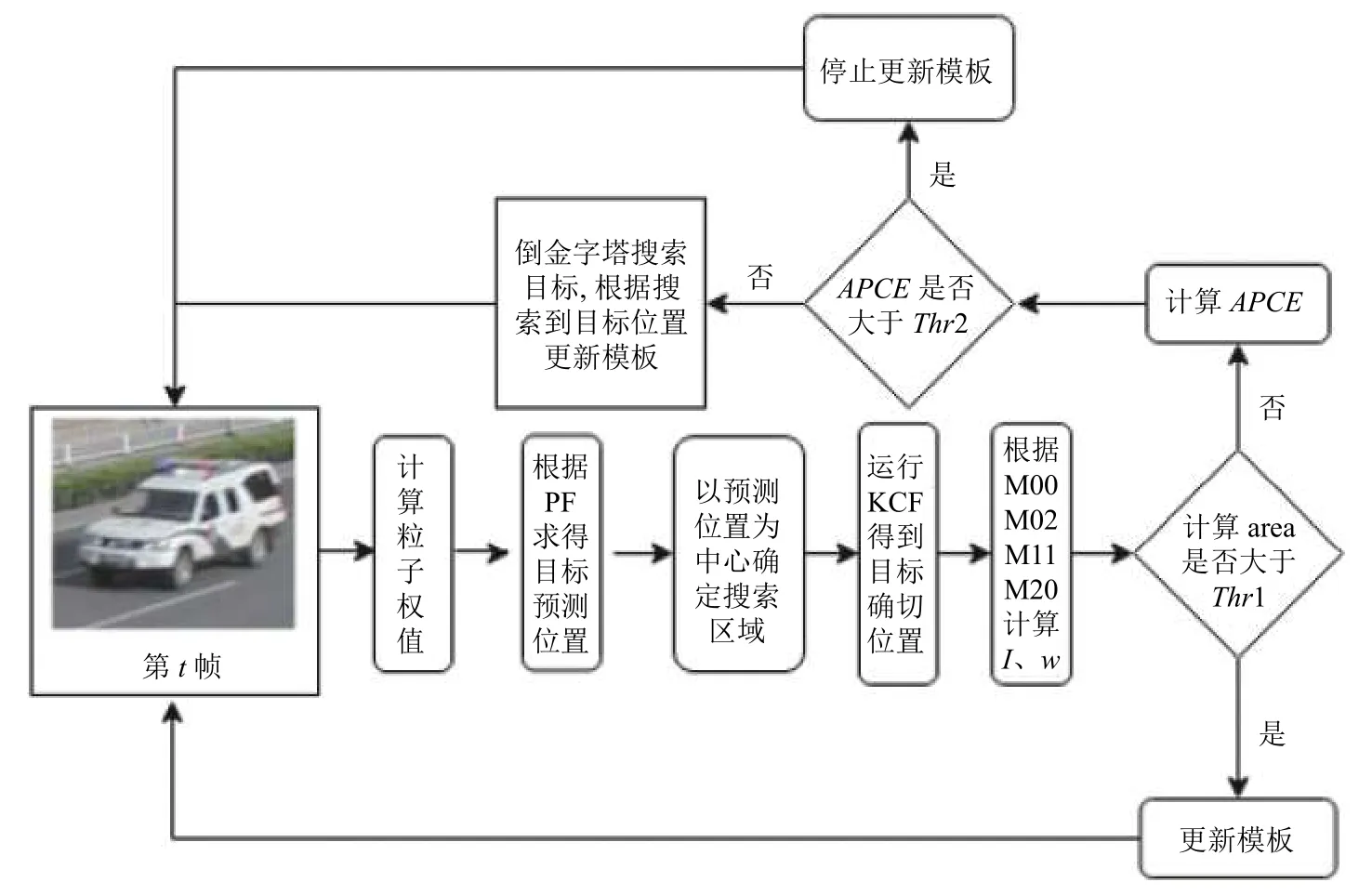
图1 KCF-PF 流程图

由于机动目标在快速运动过程中很容易出现模糊情况,如果对此不进行处理,会在每一帧更新的模板中加入背景扰动,最终影响跟踪精度.针对该问题,首先利用APCE对目标状态估计:

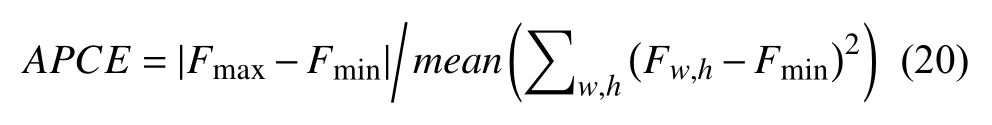
其中,Fmax与Fmin表示响应矩阵中最大、最小值.

然后APCE与预先设定阈值Thr1比较,当APCE大于Thr1时正常跟踪,小于Thr1时停止更新模板,直至当前帧APCE大于Thr1后对目标重跟踪.

考虑到跟踪过程中时间与空间的连续性,如果仅丢失一帧,目标不会移动很远,可以在上帧目标位置周围搜索,但当连续帧丢失目标时,目标可能位移到任何位置,此时需要扩大搜索范围.传统的遍历搜索方法花费时间长,为减少重跟踪时长,将视频帧划分成n个不重叠区域,用倒金字塔搜索方式进行重跟踪.倒金字塔搜索方式的迭代公式及步长计算公式如下:

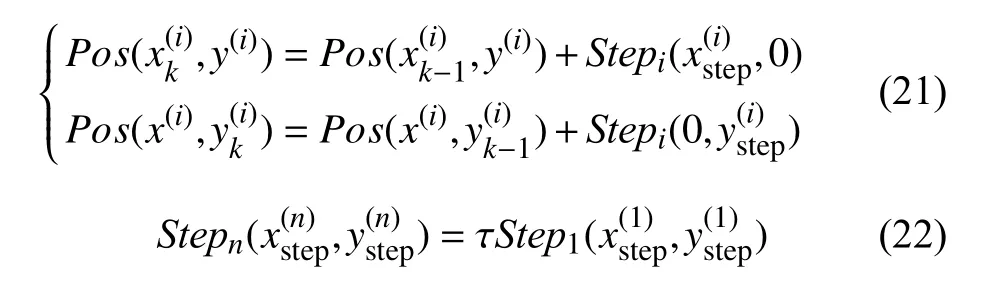
其中,x、y表示横纵坐标,式(21)中的上下两式分别表示沿着x、y方向的搜索迭代公式,Pos(·,·)表示搜索位置坐标,Step(·,·)表示搜索步长,i表示区域编号,τ表示常数.

为了更好地解释倒金字塔跟踪方式,假设只有3 个分区,分区图如图2所示.

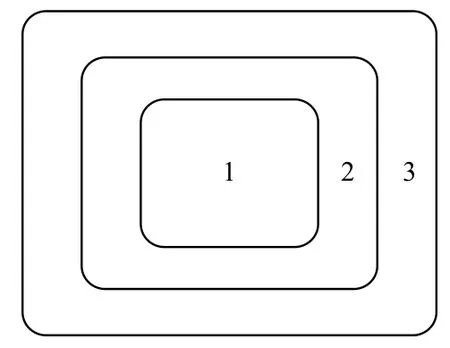
图2 倒金字塔搜索方式分区图

根据上次正确跟踪地目标位置为中心划分区域,距离中心越远搜索步长越大,第一分区是距离目标最近的搜索区域,在第一分区进行搜索时步长最短.第二分区步长是第一分区的二倍,第三分区步长是第二分区的二倍,公式如下所示:

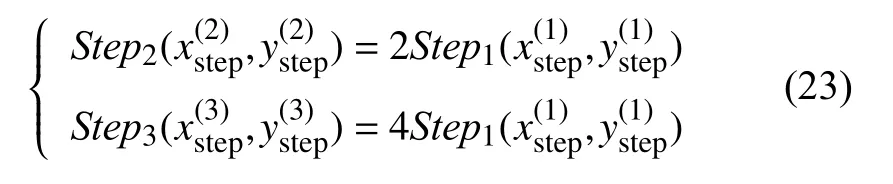
5 评价标准

为了对KCF-PF 算法量化评价,引入OTB 数据集两个评价标准:精确度(precision plot)以及成功率(success plot),下面分别对两个评价标准进行简介.

(1)Precision plot:跟踪过程中,算法估计出的目标位置称为预测值,人工标注目标位置为真实值,两者的差值小于阈值的帧数占总帧数的百分比就是精确度.一般选择20 个像素点作为阈值,给定的阈值不同,求出的precision plot 也不同.

(2)Success plot:成功率的计算用到了覆盖率公式:

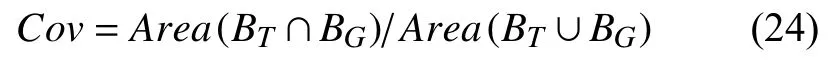
其中,BT表示运行算法得到的目标框,BG表示真实目标框,Area表示面积统计函数.如果覆盖率大于给定阈值,表明此帧成功跟踪,成功跟踪的帧数占总帧数的百分比,即成功率.一般阈值设定为0.5,给定阈值不同,success plot 也不同.

6 仿真结果及分析

6.1 参数设定

为了更好地验证新方法的准确性,设置了两组参数在不同的数据集上进行实验,实验参数如表1所示.

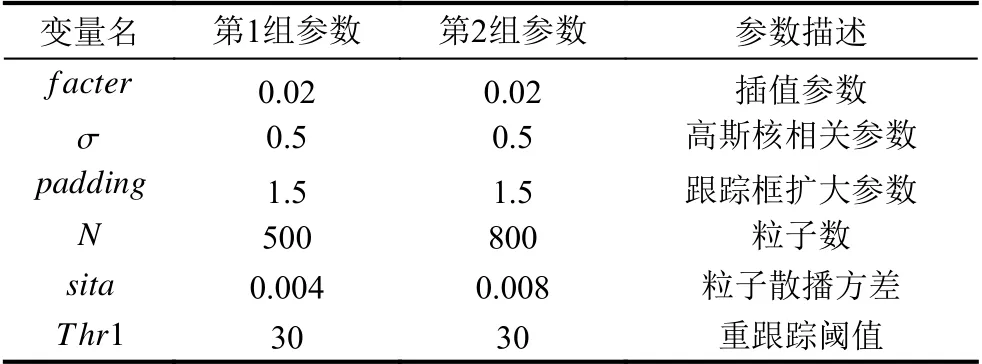
表1 实验参数

6.2 模板更新策略的阈值选定实验

Jogging 中部分视频帧与APCE关系如图3所示.

图3 目标状态分析

对图3 左边跑步女人分析,第3 帧没有遮挡及模糊情况,此时APCE大于30.第74 帧目标被遮挡,此时APCE小于10.接着对OTB100 中多个存在模糊、遮挡的视频分析后得到表2.

表2 目标状态与APCE关系表

根据以上分析,为了更好地运用历史信息并减少模糊、遮挡的影响,得到新的模板更新策略如下:

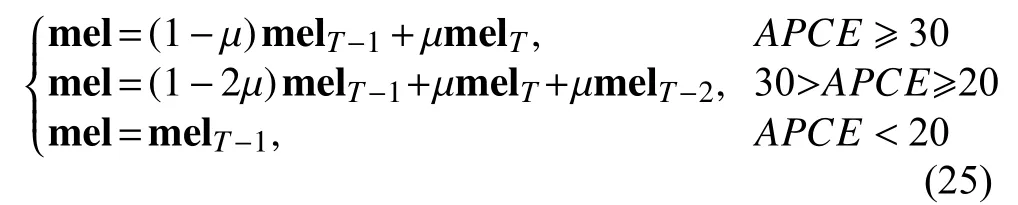
其中,μ表示常量,mel表示模板矩阵.更改模板更新策略后的KCF-PF 与其他算法性能比较如图4所示.

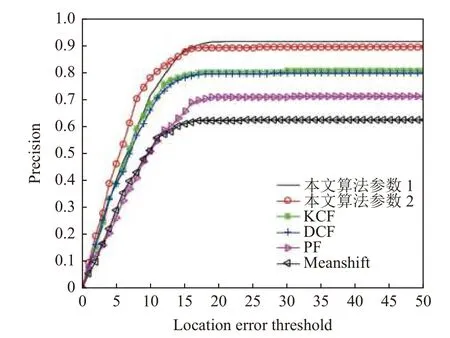
图4 算法性能比较

6.3 性能分析

与Meanshift、PF、KCF、SAMF 相比,KCF-PF在UA-DETRAC 及OTB100 数据集上有更高的识别率,具体提升如表3 和表4所示.

表3 UA-DETRAC 数据集的实验结果(%)

表4 混合OTB100 与UA-DETRAC 数据集的实验结果

6.3.1 定性分析

本节选取UA-DETRAC 视频数据集中两个视频片段进行定性分析.图5 与图6 为跟踪效果图,其中红色框是KCF-PF,黄色框是SAMF,绿色框是KCF,黑色框是PF,蓝色框是Meanshift.由图5 与图6 可以看出随着目标车辆的快速移动SAMF、KCF、PF、Meanshift都丢失了目标,而KCF-PF 可以对目标准确跟踪.

图5 由远及近车辆跟踪效果

图6 侧拍车辆跟踪效果

6.3.2 定量分析

本节对UA-DETRAC 以及OTB100 数据集进行定量分析,结果如图7所示.其中图7(a)与图7(b)是在10 个有快速移动情况车辆行驶序列中进行算法对比的结果;图7(c)与图7(d)是在25 个车辆行驶视频序列中进行算法对比的结果;图7(e)与图7(f)是在OTB100数据集中算法对比的结果;图7(g)与图7(h)是在混合了OTB100 与UA-DETRAC 数据集中算法比较的结果.

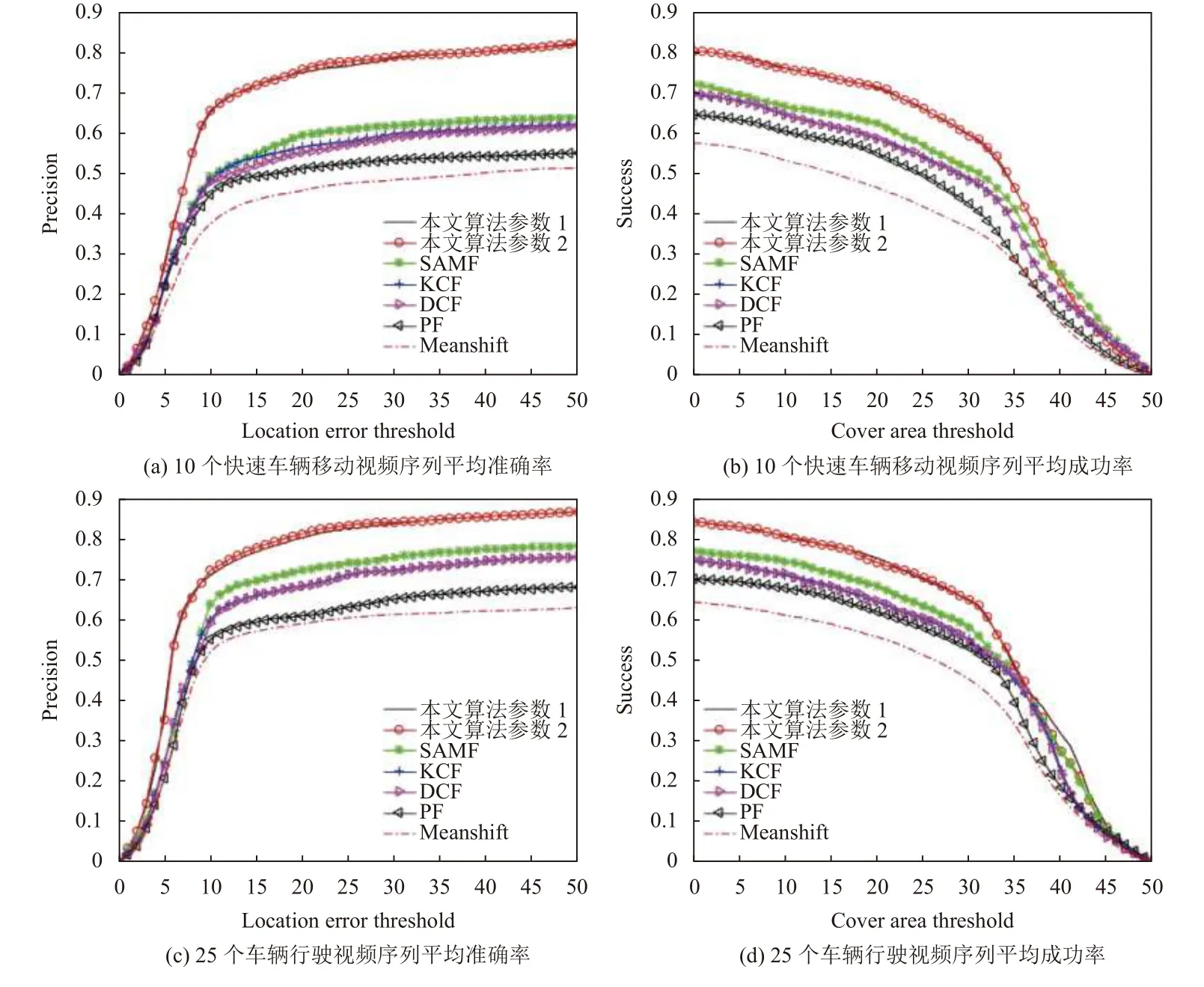
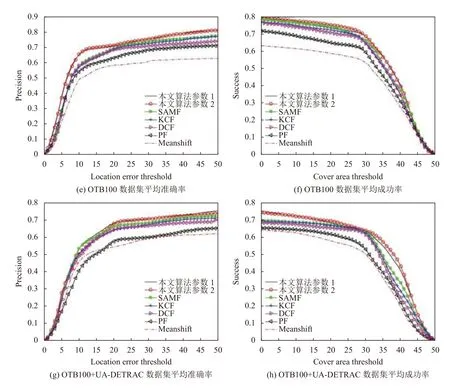
图7 定量分析图

7 结语

视频机动目标快速移动问题一直是目标跟踪问题中的难点,结合粒子滤波以及核相关滤波算法的优点,提出首先由粒子滤波算法预测目标位置,然后核相关滤波算法修正目标位置的新方法,在一定程度上解决了快速移动问题.针对形变问题加入了零截距,实现了对快速移动形变机动目标的跟踪,在原模板更新策略的基础上融入平均峰值相关能量,更好的利用了历史信息.实验结果表明,新方法可以有效地跟踪快速移动的机动目标.