长时动载作用下低路堤动力响应试验分析
韩冬卿
(中电建冀交高速公路投资发展有限公司,河北 石家庄 050051)
引言
目前我国高速公路一般采用高路堤设计方案,路堤越高填方量就越大,同时路堤自重也较大,其对路基也会产生更大的压力,也更容易造成路面下沉、路面开裂和桥头跳车等病害[1-2]。且高路基施工难度大,对机械设备要求高,施工周期长,增加了施工工期。低路堤则具有能够减少占地,与环境协调,既经济又环保的特点[3-5]。关于低路堤工程特性国内外也有许多研究,Kim通过应用特定的地基模型对无限长梁的动力特性进行了研究[6-9],赵俊明等[10-14]通过现场测试和有限元模拟相结合的手段,对振动位移的变化进行总结分析。针对交通荷载作用下低路堤动力特性方面也做了一些研究,低路堤设计因受填土高度的影响,导致路基和地基受交通动荷载的影响更加显著[15]。查文华等[16-18]通过研究不同工况下的动态响应规律,发现车轮加载的方式和基层刚度影响较为显著。但目前国内针对砾类土低路堤的研究较少,且大多停留在有限元模拟分析手段,大多存在一定的试验假设,不能精确的表现车辆通过路基时的实际工况,除此之外,工程现场的试验也受到作业环境和仪器设备的限制。本研究在传统试验基础上,对应BZZ-100 轴重下的单轮影响范围进行了研究,通过改变地基含水率模拟不同的路基的实际情况,同时,通过MTS 试验机进行荷载的施加,对路堤的受力特性进行了研究,为合理路基高度设计提供依据。
1 试验方案及原理
1.1 试验方案设计
本次试验通过设置不同土样的含水率(18%、23%和28%)来对压实、非饱和已经饱和状态的地基进行模拟。本试验开始时在对最佳含水率的土样压实,紧接着在此基础上加入定量的水,来实现不同状态的试验。本研究通过计算得出车轮的影响范围,基于此,开发了与施加情况一致的模型箱。其长度为3 m,高度为1.5米,宽度同样为1.5 m。各结构层厚度如图1所示,其中面层厚度为12 cm,采用AC-16沥青混凝土。基层厚度为40 cm,采用水泥含量为4%~6%的水泥稳定碎石。砾类土路基80 cm厚,粉质粘土地基70 cm厚。土样参数见表1。传感器样式包括动BY-1型电阻式双油腔结构土压力传感器、内埋式应变传感器与SYNERGY动态数据采集仪。土压力和动应变收集仪的安装位置见图2,路基的传感器相距20 cm,地基的传感器相距20 cm。试验模型见图3。
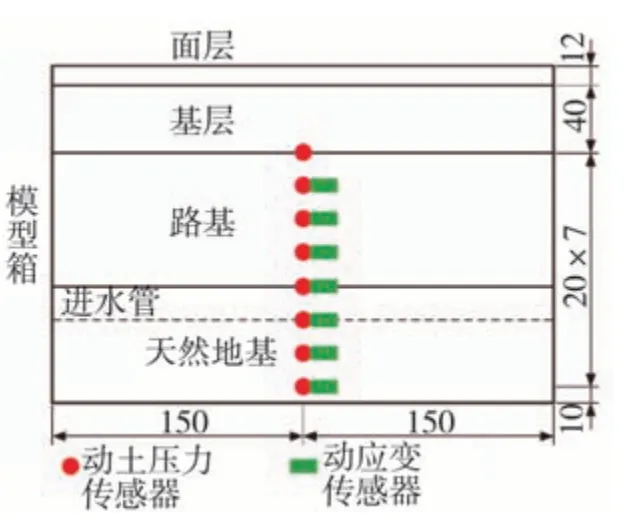
图2 传感器布置Fig.2 Sensor arrangement(unit:cm)

图3 试验模型Fig.3 Test model
1.2 加载系统及方式
采用MTS 试验系统开展试验,加载系统的荷载范围为0~100 kN,频率范围为0~10 Hz,本研究采用半正弦波动荷载进行加载,加载波形如图4所示,长时动载试验工况如表2所示,试验加载次数为10万次,频率为3 Hz。双轮组单轴轴载为100 kN,轮胎接地压强为0.7 MPa,同时采用直径为302 mm的圆形加载板模拟轮胎的接地面积。

图4 动载加载波形Fig.4 Dynamic loading waveform

表2 长时动载试验工况Table 2 Long time dynamic load test condition
2 试验数据分析
动荷载峰值为50 kN,作用频率3 Hz,同时,试验3种含水率对应不同3种土样状态,数据分析时,需要计算每一万次时,土样各深度对应的应力和应变,比如计算第10 000 次时,具体计算方法需要计算9 950 次至10 050次的试验平均值,之后每一万次的计算方法依次类推到加载的十万次终止,将采集得到数据进行整理绘制成曲线图进行分析。
2.1 应力变化规律
不同含水率(18%,23%,28%)条件下以及不同荷循环载作用次数下应力与深度关系见图5~图7。不同含水率(18%,23%,28%)条件下以及不同深度下应力与荷循环载作用次数关系见图8~图10,图中,“-0.2”等标记数字,分别代表距路面相应深度的结构层应变值,例如“-0.2”代表距路面0.2 m的结构层应变值。
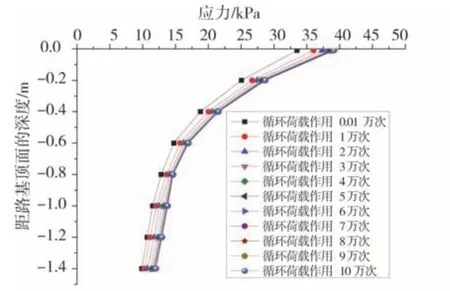
图5 18%含水率不同荷循环载作用次数下应力与深度关系Fig.5 Relationship between stress and depth under different times of cyclic loading under 18%moisture content

图6 23%含水率不同荷循环载作用次数下应力与深度关系Fig.6 Relationship between stress and depth under different times of cyclic loading under 23%moisture content

图7 28%含水率不同荷循环载作用次数下应力与深度关系Fig.7 Relationship between stress and depth under different times of cyclic loading under 28%moisture content
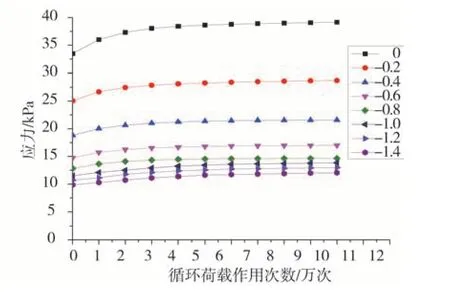
图8 18%含水率不同深度处应力与荷循环载作用次数的关系Fig.8 Relationship between stress at different depths and times of cyclic loading under 18%moisture content

图10 28%含水率不同深度处应力与荷循环载作用次数的关系Fig.10 Relationship between stress at different depths and times of cyclic loading under 28%moisture content

图9 23%含水率不同深度处应力与荷循环载作用次数的关系Fig.9 Relationship between stress at different depths and times of cyclic loading under 23%moisture content
由图5~图10中可知,随着动荷载的不断作用,距离路基顶面的各个距离的受力也都增大,土样的应力累计逐渐减小,存在一定的累计效应。本研究提出累计速度(荷载作用次数的应力与初始应力差值与初始应力的比值),由此可以计算得出3种土样状态的实际情况,当荷载作用完毕时,路基的应力累计速率为17.1%、18.2和16.1%,地基的累计速率为13.9%、12.8%和17.9%。
从图5~图7中可知,地基含水率及荷载不变时,深度越深,应力的衰减越明显,同时该衰减形式呈非线性,其中,系数η可通过以下函数获得:

式中,Z为离路基深度,ξ、ψ为试验系数。
荷载作用完毕时,3种不同状态地基,对应的相关系数见表3。

表3 ξ、ψ和R2的值Table 3 Values of ξ、ψ and R2
由表3可知,R2都比0.968大,所以采用上式计算是满足显示需求的。
2.2 应变变化规律
3种地基不同含水率各结构层的应变与深度关系见图11~图13。不同含水率各结构层应变与动荷载作用次数关系见图14~图16,图中“-0.2”等标记数字,分别代表距路面相应深度的结构层应变值,例如“-0.2”代表距路面0.2 m的结构层应变值。

图11 18%含水率时各结构层的应变与深度的关系Fig.11 The relationship between strain and depth of each structural layer at 18%water content
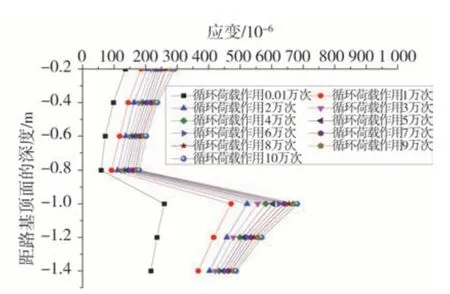
图12 23%含水率时各结构层的应变与深度的关系Fig.12 The relationship between strain and depth of each structural layer at 23%water content

图13 28%含水率时各结构层的应变与深度的关系Fig.13 The relationship between strain and depth of each structural layer at 28%water content
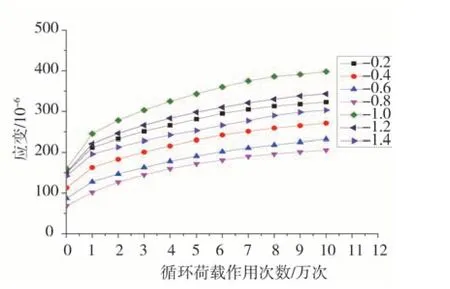
图14 18%含水率时各结构层应变与动荷载作用次数的关系Fig.14 The relationship between the strain of each structural layer and the number of dynamic loads at 18%moisture content
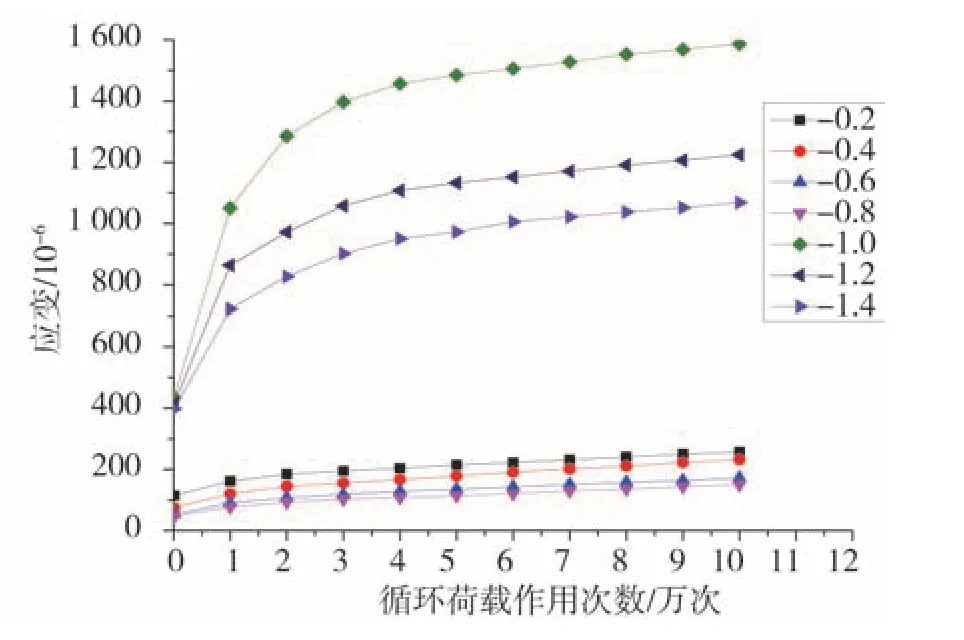
图16 28%含水率时各结构层应变与动荷载作用次数的关系Fig.16 The relationship between the strain of each structural layer and the number of dynamic loads at 28%moisture content

图15 23%含水率时各结构层应变与动荷载作用次数的关系Fig.15 The relationship between the strain of each structural layer and the number of dynamic loads at 23%moisture content
三种地基,当荷载作用不变时,道路的深度增加,其对应的应变呈现下降趋势,道路路基范围内的应变也会下降,与此同时,动荷载作用次数增加会导致道路范围内的应变会出现累计,当荷载作用次数在0 ~3万次时,相关应变增加较快,但是当作用次数超过3万次时,相关应变的增长逐渐减缓。当含水率为28%时,比含水率为18%的积累更为明显。当荷载作用完毕时,18%含水率路基对应的累积速率为115%,地基对应的累积速率为148%;23%含水率路基对应的累积速率为115%,地基对应的累积速率为163%;28%含水率路基对应的累积速率为123%,地基对应的累积速率为265%;所以3种地基应变累积率大于路基对应的累积率。
2.3 动应力累积模型
本研究对应的累积模型可采用下式表示:

式中,σ0为路基顶面动应力,σ为应力累积值,N为荷载作用次数,a、b和c为试验的参数。
本研究根据以上试验结果,通过计算求得对应的试验参数a、b和c,对应模型可用式(3)~(6)表示:
地基含水率为18%、动荷载峰值为50 kN时:

地基含水率为23%、动荷载峰值为50 kN时:

地基含水率为28%、动荷载峰值为50 kN时:

地基含水率为18%、动荷载峰值为70 kN时:

模型计算与实测对比如图17。从图中可以看出,实测得到的结果和模型计算的结果比较接近,所以本研究所计算的结果较为准确,可以进行模型的应用,以此来计算相关的动应力。综合以上公式求得地基和路堤下对应的σz计算公式:
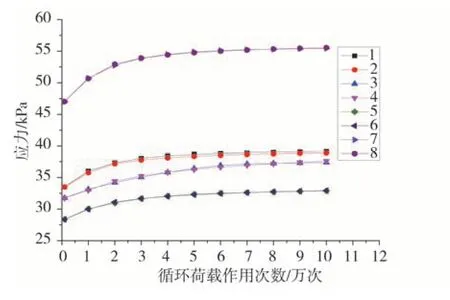
图17 不同动荷载作用次数下路基顶面动应力模型计算值与实测值对比Fig.17 Comparison of calculated and measured values of dynamic stress model on the top of subgrade under different dynamic load action times

通过上式的计算,可求得不同荷载作用对应的模型值,计算结果和实际情况对比见图18。由图18可知,实测结果和模型计算结果较为接近,因此本研究采用的计算公式可以满足实际需求。
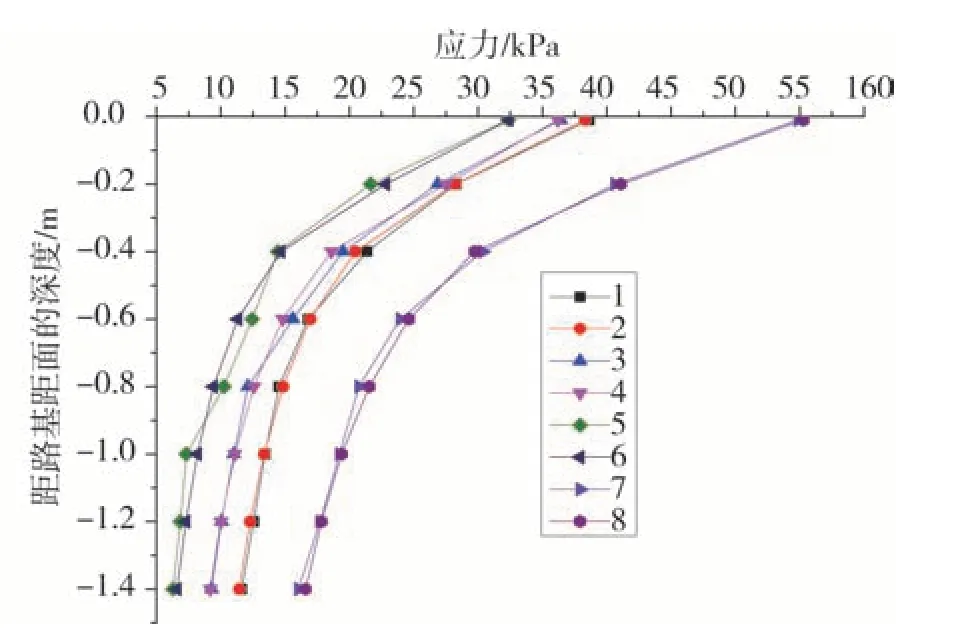
图18 荷载作用5万次时各深度处动应力模型结果与实测结果对比Fig.18 Comparison of the calculated value and the measured value of the dynamic stress model at each depth when the load is applied for 50,000 time
图17~图18 中,1 代表压实状态,荷载峰值为50 kN 的实测值,2 代表压实状态,荷载峰值为50 kN 的计算值,3代表非饱和状态,荷载峰值为50 kN的实测值,4代表非饱和状态,荷载峰值为50 kN的计算值,5代表饱和状态,荷载峰值为50 kN 的实测值,6 代表饱和状态,荷载峰值为50 kN 的计算值,7 代表压实状态,荷载峰值为70 kN的实测值,8代表压实状态,荷载峰值为70 kN的计算值。
3 结论
文中针对砾类土低路堤特性进行室内足尺模型试验,采用长时施加动荷载方式探究路基和地基范围内不同深度处的应力和不同结构层的应变变化规律,提出了应力衰减系数及动应力累计模型,得到如下结论:
(1)地基含水率及荷载不变时,应力随深度增加而快速衰减,基于大量试验数据,统计分析得到了不同状态地基的应力衰减系数方程。
(2)地基含水率越大,地基范围内各层应变累积效应越明显,且在各含水率状态下地基应变累积率均大于路基部分应变累积率。
(3)通过对大量数据的统计模拟分析,提出了长时动载作用下低路堤路基和地基范围内动应力累积模型。

