无保持架轴承滚动体与变速曲面静接触有限元

赵彦玲，王明珠，侯新新，秦生

摘要：满装轴承因去掉保持架而使承载能力提高且轻量化，目前已经受到国内外学者的关注，但针对滚动体接触的理论研究较少。提出在外圈滚道增加局部变速曲面来改变滚动体与滚道接触状态的原理，基于赫兹理论建立滚动体与滚道接触力及接触应力模型，分析变速曲面参数对滚动体间及滚道接触状态影响因素;通过有限元数值模拟对滚动体与滚道、滚动体与变速曲面进行仿真并获得可量化参数，确定滚动体进出变速曲面接触应力及应变的变化规律;结合物理样机对所设计的变速曲面进行磨损试验，用于验证理论的正确性。结果表明滚动体与变速曲面边缘接触力大于中间位置，相邻滚动体滚过变速曲面时处于非接触状态。本研究为无保持架球轴承动态磨损提供理论基础。

关键词：无保持架球轴承;变速曲面;赫兹理论;接触模型;有限元

DOI：10.15938/j.jhust.2022.01.013

中图分类号： TH133.3       文献标志码： A          文章编号： 1007-2683（2022）01-0100-08

Finite Element of Static Contact between Rolling Element

and Raceway of Cageless Ball Bearing

ZHAO Yanling1，WANG Mingzhu1，HOU Xinxin2，QIN Sheng3

（1.School of Mechanical and Power Engineering， Harbin University of Science and Technology， Harbin 150080，China;

2.SUNNY GROUP CO.，LTD.，Yuyao 315400，China; 3.Second Port Branch of Rizhao Port Co.， Ltd，Rizhao 276826，China）

Abstract：At present， scholars at home and abroad have paid attention to the improvement of bearing capacity and lightweight due to the removal of cage， but the theoretical research on rolling element contact is less. The principle of adding local variable speed surface to outer ring raceway to change the contact state between rolling element and raceway is proposed. Based on Hertz theory， the contact force and contact stress model between rolling element and raceway are established， and the influence factors of variable speed surface parameters on contact state between rolling elements and raceway are analyzed. Through finite element numerical simulation， the rolling element and raceway， rolling element and variable speed surface are simulated and obtained. The change law of contact stress and strain of the rolling element in and out of the variable speed surface is determined by quantifiable parameters， and the wear test of the designed variable speed surface is carried out with the physical prototype to verify the correctness of the theory. The results show that the contact force between the rolling body and the variable speed surface edge is greater than that at the middle position， and the adjacent rolling body is in noncontact state when rolling through the variable speed surface. This study provides a theoretical basis for the dynamic wear of no cage ball bearings.

Keywords：cageless ball bearing; variable speed surface; hertz theory; contact model; finite element

0引言

近年來，随着航空发动机、电主轴以及无人机技术的发展，对滚动轴承的结构、材质和转速要求越来越高，将工程陶瓷材料引入轴承中可大幅提升轴承的服役性能和应用范围[1]。虽然深沟球轴承具有较小的摩擦系数，但在高速运转情况下，保持架与滚动体和套圈之间的摩擦会产生不可忽视的阻力，致使轴承发热，从而限制了轴承的极限转速。为了避免保持架所带来的摩擦阻力，国内外出现了无保持架球轴承。虽然无保持架结构使轴承滚动体的数目更多，提高了轴承的承载能力，但滚动体之间的接触和摩擦使无保持架球轴承多用于低速重载工况下。本文开展了无保持架球轴承滚动体与滚道接触相关问题的研究。

国内外学者在轴承静接触分析方面展开了一定的理论方法研究。樊洪辉[2]提出了一种数值模拟满装滚子轴承扭矩的研究方法，通过ADAMS的微分方程求解器，对满装圆柱滚子轴承进行仿真分析，计算滚子与内圈、滚子与滚子、滚子与外圈的摩擦力和扭矩;进而在文[3]针对低速重载工况下满装圆柱滚子轴承的运动问题，通过改变ADAMS中设置的轴承内圈的转速，对NCF3004CV轴承不同转速下的滚子与内圈接触力以及内圈质心运动轨迹进行仿真研究;侯新新[4]针对带变速曲面的无保持架球轴承进行摩擦磨损性能分析，对滚动体与变速曲面的接触形式和受力状态分析，建立滚动体与变速曲面处的接触力学模型，并对其磨损失效时间进行预测;赵彦玲等[5]针对钢球在展开机构中的接触碰撞特性进行分析，建立了钢球与展开轮的Hertz接触碰撞模型获得了碰撞力的变化过程;并在文[6]中针对钢球缺陷检测过程中，镜面钢球打滑导致展开轮磨损这一问题，结合试验与有限元的方法，得到适合于展开轮的材料与微结构;潘承怡等[7]针对展开轮寿命预测问题，根据展开轮结构和展开原理建立展开轮的临界失效条件，并利用ANSYS有限元软件对展开轮磨损进行数值模拟，得到磨损深度与磨损次数的关系方程;Peter ulka等[8]针对滚动轴承的静接触压力、应力进行分析，建立了赫兹理论静接触压力计算模型，通过ANSYS Workbench进行仿真，得到了最大静接触压力值;李英等[9]针对自润滑关节轴承的接触应力分布进行分析，采用Winkler模型建立了自接触应力解析模型，并利用ANSYS 软件对轴承受径向载荷和轴向载荷时的接触应力分布进行分析;卢黎明等[10]针对滚滑轴承零件的应力分布、变化规律及疲劳寿命进行分析，通过ABAQUS有限元软件的隐式算法对滚滑轴承进行多体接触静力学的仿真;Raju D V等[11]采用通用有限元软件ABAQUS精确地预测了汽车轮毂滚珠轴承的接触应力、轴承载荷和轴承寿命，并在赫兹接触理论的基础上，给出了各载荷情况下的理论接触应力计算;Anoopnath P. R.等[12]基于Hertz接触理论对滚动体与滚道之间的接触机理进行了研究，并利用MESYS工具进行了相应的数值分析。由结果可以看出，MESYS结果与公式结果的变化很小，低于5%;胡宝根等[13]针对自润滑关节轴承衬垫的应力分布、接触应力变化和变形情况进行分析，建立了自润滑关节轴承的有限元模型，得出衬垫的静接触应力分布;张胜伦等[14]针对角接触球轴承的结构参数对接触应力的影响进行分析，建立了赫兹理论计算模型，通过有限元法分析了结构参数对静接触应力的影响;Xian等[15]针对球与滚道的静接触特性进行研究，建立了赫兹理论接触模型，分析了轴承结构参数对静接触应力的影响;Xi等[16]提出了跨尺度三维有限元模拟方法，通过对深沟球轴承与滚道进行了非赫兹弹塑性静接触分析，研究了载荷大小和方向对接触状态的影响;WANG等[17]针对大接触角推力球轴承的接触特性进行分析，依据赫兹弹性接触理论并采用有限元法对轴承的三维模型进行非线性接触仿真，分析应力和变形情况;郑晓猛[18]等研究了一种快速、简单的材料滚滑接触内部应力的计算方法以替代耗时长的有限元法，通过Hertz接触理论计算最大接触应力及尺寸，并基于MATLAB实现滚滑接触内部应力场的计算，该方法简单方便，便于结合其他应力求真实应力场，对材料组织演变有着重要的意义。

综合国内外研究现状，虽然已有对轴承滚动体与滚道接触的研究，但还未发现对无保持架球轴承滚动体与滚道接触的研究，缺少相应的理论基础。因此本文主要研究无保持架球轴承滚动体与滚道的接触应力分布，采用理论计算和有限元分析相结合的方法并通过物理样机实验验证理论分析与仿真实验结果的一致性，为无保持架球轴承的磨损研究提供理论基础。

1滚动体与滚道接触状态分析

1.1轴承外圈局部变速曲面设计

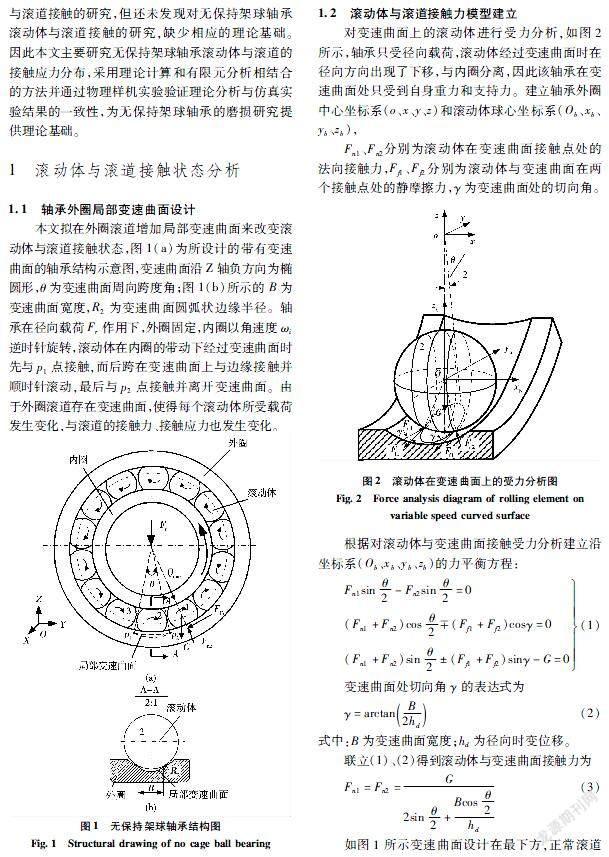
本文拟在外圈滚道增加局部变速曲面来改变滚动体与滚道接触状态，图1（a）为所设计的带有变速曲面的轴承结构示意图，变速曲面沿Z轴负方向为椭圆形，θ为变速曲面周向跨度角;图1（b）所示的B为变速曲面宽度，R2为变速曲面圆弧状边缘半径。轴承在径向载荷Fr作用下，外圈固定，内圈以角速度ωi逆时针旋转，滚动体在内圈的带动下经过变速曲面时先与p1点接触，而后跨在变速曲面上与边缘接触并顺时针滚动，最后与p2点接触并离开变速曲面。由于外圈滚道存在变速曲面，使得每个滚动体所受载荷发生变化，与滚道的接触力、接触应力也发生变化。

1.2滚动体与滚道接触力模型建立

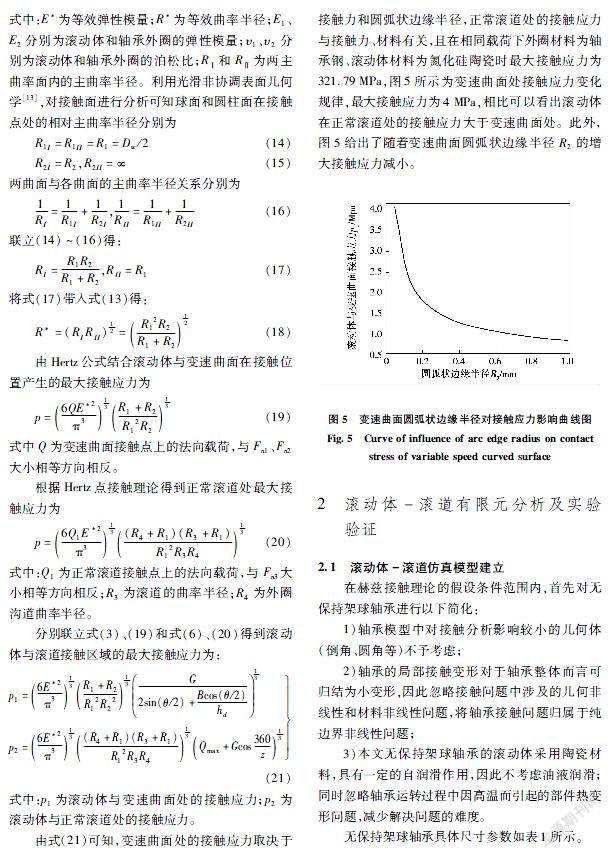
对变速曲面上的滚动体进行受力分析，如图2所示，轴承只受径向载荷，滚动体经过变速曲面时在径向方向出现了下移，与内圈分离，因此该轴承在变速曲面处只受到自身重力和支持力。建立轴承外圈中心坐标系（o、x、y、z）和滚动体球心坐标系（Ob、xb、yb、zb），

Fn1、Fn2分别为滚动体在变速曲面接触点处的法向接触力，Ff1、Ff2分别为滚动体与变速曲面在两个接触点处的静摩擦力，γ为变速曲面处的切向角。

根据对滚动体与变速曲面接触受力分析建立沿坐标系（Ob、xb、yb、zb）的力平衡方程：

Fn1sinθ2-Fn2sinθ2=0

（Fn1+Fn2）cosθ2（Ff1+Ff2）cosγ=0

（Fn1+Fn2）sinθ2±（Ff1+Ff2）sinγ-G=0（1）

變速曲面处切向角γ的表达式为

γ=arctanB2hd（2）

式中：B为变速曲面宽度;hd为径向时变位移。

联立（1）、（2）得到滚动体与变速曲面接触力为

Fn1=Fn2=G2sinθ2+Bcosθ2hd（3）

如图1所示变速曲面设计在最下方，正常滚道上滚动体1和3受载最大，以滚动体1分析，基于Stribeck理论可得到滚动体1受到的载荷为

Qmax=5Fr（Z-1）cos360Z（4）

根据图1滚动体与滚道接触受力分析[19]建立滚动体沿Y、Z坐标轴的力平衡方程为

Fn3sin360z=Ff3cos360z+Qmaxsin360z

Fn3cos360z+Ff3sin360z=G+Qmaxcos360z（5）

式中：Fn3为滚动体在正常滚道接触点处的法向接触力;Ff3为滚动体与正常滚道接触点处的静摩擦力;z为滚动体个数。

整理得到滚动体1与滚道接触力为

Fn3=Qmax+Gcos360Z（6）

由式（3）和式（5）可知，变速曲面处的接触力取决于其跨度角和宽度，正常滚道处的接触力与滚动体的数量、材料有关，且在相同载荷下滚动体数量14、材料为氮化硅陶瓷时最大接触力为17.371N。

图3所示为变速曲面处接触力变化规律，最大接触力为1.9×10-4N，相比可以看出滚动体在正常滚道处的接触力远远大于变速曲面处。此外，图3给出了随着变速曲面跨度角θ的增大、宽度B的减小接触力增大。

1.3滚动体与滚道接触应力模型建立

为避免变速曲面的尖锐边缘在轴承运转过程中发生弹塑性变形，将变速曲面的锋利边缘假设成圆弧状，因此滚动体与变速曲面边缘的接触类型为点接触。根据Hertz接触理论[20]可知承载时由接触点扩展成如图4所示的椭圆形接触面，其应力分布为半椭球形，O1为椭圆形接触面中心，a为接触椭圆长半轴，b为接触椭圆短半轴，R1为滚动体半径，R2为圆弧状边缘半径。

滚动体在变速曲面中间位置时接触区域内任意一点应力分布为

p（x，y）′=3Q2πab1-xa2-yb2（7）

接触椭圆长半轴与短半轴分别为

a=μ×3321-υ12E1+1-υ22E23Q∑ρ（8）

b=v×3321-υ12E1+1-υ22E23Q∑ρ（9）

式中：μ和v是由F（ρ）所决定的系数，根据轴承规范获得;∑ρ为接触面主曲率之和，其表达式为：

∑ρ=ρ1Ι+ρ1Π+ρ2Ι+ρ2Π（10）

式中ρ1Ι、ρ1Π和ρ2Ι、ρ2Π分别为滚动体与变速曲面两侧接触面的主曲率。

椭圆中心O1是接触区内的最大接触应力点，其表达式为

p=3Q2πab=6QE*2π3R*213（11）

1E*=1-υ12E1+1-υ22E2（12）

R*=（RΙRΠ）12（13）

式中：E*为等效弹性模量;R*为等效曲率半径;E1、E2分别为滚动体和轴承外圈的弹性模量;υ1、υ2分别为滚动体和轴承外圈的泊松比;RⅠ和RⅡ为两主曲率面内的主曲率半径。利用光滑非协调表面几何学[13]，对接触面进行分析可知球面和圆柱面在接触点处的相对主曲率半径分别为

R1Ι=R1Π=R1=Dw/2（14）

R2Ι=R2，R2Π=∞（15）

两曲面与各曲面的主曲率半径关系分别为

1RΙ=1R1Ι+1R2Ι，1RΠ=1R1Π+1R2Π（16）

联立（14）～（16）得：

RΙ=R1R2R1+R2，RΠ=R1（17）

将式（17）带入式（13）得：

R*=（RΙRΠ）12=R12R2R1+R212（18）

由Hertz公式结合滚动体与变速曲面在接触位置产生的最大接触应力为

p=6QE*2π313R1+R2R12R213（19）

式中Q为变速曲面接触点上的法向载荷，与Fn1、Fn2大小相等方向相反。

根据Hertz点接触理论得到正常滚道处最大接触应力为

p=6Q1E*2π313（R4+R1）（R3+R1）R12R3R413（20）

式中：Q1为正常滚道接触点上的法向载荷，与Fn3大小相等方向相反;R3为滚道的曲率半径;R4为外圈沟道曲率半径。

分别聯立式（3）、（19）和式（6）、（20）得到滚动体与滚道接触区域的最大接触应力为：

p1=6E*2π313R1+R2R12R2213G2sin（θ/2）+Bcos（θ/2）hd13

p2=6E*2π313（R4+R1）（R3+R1）R12R3R413Qmax+Gcos360z13（21）

式中：p1为滚动体与变速曲面处的接触应力;p2为滚动体与正常滚道处的接触应力。

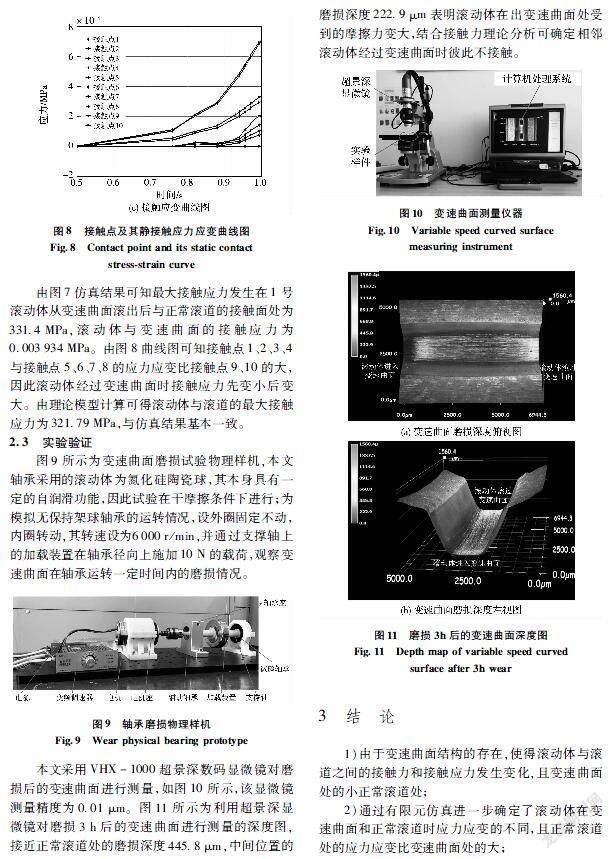
由式（21）可知，变速曲面处的接触应力取决于接触力和圆弧状边缘半径，正常滚道处的接触应力与接触力、材料有关，且在相同载荷下外圈材料为轴承钢、滚动体材料为氮化硅陶瓷时最大接触应力为321.79MPa，图5所示为变速曲面处接触应力变化规律，最大接触应力为4MPa，相比可以看出滚动体在正常滚道处的接触应力大于变速曲面处。此外，图5给出了随着变速曲面圆弧状边缘半径R2的增大接触应力减小。

2滚动体-滚道有限元分析及实验验证

2.1滚动体-滚道仿真模型建立

在赫兹接触理论的假设条件范围内，首先对无保持架球轴承进行以下简化：

1）轴承模型中对接触分析影响较小的几何体（倒角、圆角等）不予考虑;

2）轴承的局部接触变形对于轴承整体而言可归结为小变形，因此忽略接触问题中涉及的几何非线性和材料非线性问题，将轴承接触问题归属于纯边界非线性问题;

3）本文无保持架球轴承的滚动体采用陶瓷材料，具有一定的自润滑作用，因此不考虑油液润滑;同时忽略轴承运转过程中因高温而引起的部件热变形问题，减少解决问题的难度。

无保持架球轴承具体尺寸参数如表1所示。

本文轴承的内、外圈材料为轴承钢（GCR1-5），滚动体材料为氮化硅陶瓷球，其二者材料的具体属性参数如表2所示。

由于无保持架球轴承的外圈存在变速曲面，所以需要对变速曲面接触位置的网格进行细化。无保持架球轴承模型网格划分主要采用类型为C3D8R的六面体，其中设置内外圈的网格尺寸为1mm，滚动体的网格尺寸为0.3mm，变速曲面的网格最大尺寸为0.15mm。其网格划分如图6所示。

如图6所示，在进行仿真分析时采用外圈固定、内圈受载的方式，故施加的边界条件如下：首先约束轴承外圈外圆表面所有节点在x、y、z 3个方向上的平动和转动自由度;由于本文的无保持架球轴承是用在高速轻载下，为模拟该工况，在z方向对轴承内圈施加载荷50N;为模拟重力对轴承的影响，对轴承整体施加z轴负方向上的重力加速度。

2.2滚动体-滚道数值模拟分析

根据有限元仿真计算得到轴承在径向载荷下的静力仿真应力应变云图及曲线图，分别如图7、图8所示。

由图7仿真结果可知最大接触应力发生在1号滚动体从变速曲面滚出后与正常滚道的接触面处为331.4MPa，滚动体与变速曲面的接触应力为0.003934MPa。由图8曲线图可知接触点1、2、3、4与接触点5、6、7、8的应力应变比接触点9、10的大，因此滚动体经过变速曲面时接触应力先变小后变大。由理论模型计算可得滚动体与滚道的最大接触应力为321.79MPa，与仿真结果基本一致。

2.3实验验证

图9所示为变速曲面磨损试验物理样机，本文轴承采用的滚动体为氮化硅陶瓷球，其本身具有一定的自润滑功能，因此试验在干摩擦条件下进行;为模拟无保持架球轴承的运转情况，设外圈固定不动，内圈转动，其转速设为6000r/min，并通过支撑轴上的加载装置在轴承径向上施加10N的载荷，观察变速曲面在轴承运转一定时间内的磨损情况。

本文采用VHX-1000超景深数码显微镜对磨损后的变速曲面进行测量，如图10所示，该显微镜测量精度为0.01μm。图11所示为利用超景深显微镜对磨损3h后的变速曲面进行测量的深度图，接近正常滚道处的磨损深度445.8μm，中间位置的磨损深度222.9μm表明滚动体在出变速曲面处受到的摩擦力变大，结合接触力理论分析可确定相邻滚动体经过变速曲面时彼此不接触。

3结论

1）由于变速曲面结构的存在，使得滚动体与滚道之间的接触力和接触应力发生变化，且变速曲面处的小正常滚道处;

2）通过有限元仿真进一步确定了滚动体在变速曲面和正常滚道时应力应变的不同，且正常滚道处的应力应变比变速曲面处的大;

3）通过实验说明了滚动体经过变速曲面时的磨损深度比正常滚道处的小，摩擦力变大;

4）滚动体滚过变速曲面时接触状态发生改变，使相邻滚动体处于非接触状态。

参 考 文 献：

[1]谢天舒. 氮化硅陶瓷轴承外圈磨削的双目标工艺优化[J]. 金刚石与磨料磨具工程， 2021， 41（4）： 82.

XIE Tianshu. Two Objective Process Optimization for Grinding of Outer Ring of Silicon Nitride Ceramic Bearing[J]. Diamond & Abrasive Engineering， 2021， 41（4）： 82.

[2]樊洪辉.满装滚子轴承扭矩的实验与仿真分析[J].计量与测试技术，2019，46（4）：28.

FAN Honghui. Experiment and Simulation Analysis of Full Roller Bearing Torque[J]. Metrology & Measurement Technique， 2019，46（4）：28.

[3]樊洪辉，俞扬飞，陈晓萌.基于ADAMS的满装圆柱滚子轴承性能分析[J].计量与测试技术，2019，46（7）：40.

FAN Honghui， YU Yangfei， CHEN Xiaomeng. Performance Analysis of Fullfilled Cylindrical Roller Bearing Based on ADAMS[J]. Metrology & Measurement Technique. 2019，46（7）：40.

[4]侯新新. 無保持架球轴承变速曲面摩擦磨损性能研究[D].哈尔滨：哈尔滨理工大学，2020.

[5]赵彦玲，李积才，赵志强，等.钢球展开机构的接触碰撞特性[J].哈尔滨理工大学学报，2015，20（6）：37.

ZHAO Yanling， LI Jicai， ZHAO Zhiqiang， et al. Contactimpact Characteristic Research on Unfolding Mechanism of Steel Ball[J]. Journal of Harbin University of Science and Technology， 2015，20（6）：37.

[6]赵彦玲，张经纬，侯新新，等.微结构钢球展开轮增摩降磨特性分析[J].哈尔滨理工大学学报，2018，23（5）：8.

ZHAO Yanling，ZHANG Jingwei，HOU Xinxin， et al. Analysis of Friction and Wear Characteristics of Steel Ball Expansion Wheel Based on Microstructures[J]. Journal of Harbin University of Science and Technology， 2018，23（5）：8.

[7]潘承怡，李侠，赵彦玲，等.应用数值模拟的钢球检测展开轮磨损寿命预测[J].哈尔滨理工大学学报，2020，25（2）：50.

PAN Chengyi，LI Xia，ZHAO Yanling，et al. Wear Life Prediction on Unfolding Wheel of Steel Ball Detection by Using Numerical Simulation[J]. Journal of Harbin University of Science and Technology， 2020，25（2）：50.

[8]ULKA， Peter， Sapietová， Albeta， Dek， Vladimír， et al. Static Structural Analysis of Rolling Ball Bearing[J].MATEC Web of Conferences，2018，244.

[9]李英，李宝福，李如琰.自润滑关节轴承接触应力分析[J].轴承，2016（5）：32.

LI Ying， LI Baofu， LI Ruyan. Analysis on Contact Stress of Self Lubricating Spherical Plain Bearings[J]. Bearing， 2016（5）：32.

[10]卢黎明，余云云，曾国文，卢晋夫.基于ABAQUS的滚滑轴承静力学分析[J].现代制造工程，2018（8）：92.

LU Liming， YU Yunyun， ZENG Guowen， et al. Static Analysis of Rollingsliding Bearing Based on ABAQUS[J]. Modern Manufacturing Engineering， 2018（8）：92.

[11]RAJU D. V.， DIXIT Pravin， RATHORE Nitin， et al. Bearing Life Evaluation of Wheel Hub Ball Bearing Based on Finite Element Analysis[J]. Journal of Tribology， 2018， 140（5）：1.

[12]P.R.ANOOPNATH， V. SURESH BABU， A.K. VISHWANATH. Hertz Contact Stress of Deep Groove Ball Bearing. 2018， 5（2）：3283.

[13]胡宝根，王卫英，岳琳琳.基于有限元法的自润滑关节轴承静力学分析[J].轴承，2014（4）：10.

HU Baogen， WANG Weiying， YUE Linlin. Statics Analysis of SelfLubricating Spherical Plain Bearings Based on FEM[J]. Bearing， 2014（4）：10.

[14]张胜伦，徐华，买买提明·艾尼，等.角接触球轴承的结构参数对接触应力的影响及优化[J].轴承，2016（6）：12.

ZHANG Shenglun， XU Hua， MAMTIMIN Geni， et al. Effect and Optimization of Structural Parameters of Angular Contact Ball Bearings on Contact Stress[J]. Bearing， 2016（6）：12.

[15]FENG X Y， LI H， YUE M J， et al. Study on Contact Characteristic of Globoidal Continuous Cam with Ball[J].Applied Mechanics and Materials，2012，121：1254.

[16]XI Q， PI Y， HU Y. A NonHertzian Contact Analysisfor the Ball and Raceway of a Deep Groove Ball Bearing[J].IOP Conference Series Materials Science and Engineering，2019，542：012025.

[17]HUAI W， SHUANG D. Study on Contact Finite Element Simulation of the HighAngular Contact Thrust Ball Bearing[J].Computer Simulation，2013，30（1）：305.

[18]郑晓猛，杜三明，张永振，等.基于Matlab计算滚动轴承滚滑接触内部应力分布[J].润滑与密封，2020，45（7）：52.

ZHENG Xiaomeng， DU Sanming， ZHANG Yongzhen， et al. Calculation of Stress Field in RollingSlip Contact of Rolling Bearings Based on Matlab[J]. Lubrication Engineering， 2020，45（7）：52.

[19]王黎钦.滚动轴承的极限設计[M].哈尔滨：哈尔滨工业大学出版社， 2013.

[20]ZHAO Yanling， XIA Chengtao， WANG Hongbo， et al. Analysis and Numerical Simulation of Rolling Contact Between Sphere and Cone[J].Chinese Journal of Mechanical Engineering，2015，28（3）：521.

（编辑：王萍）