模糊云资源调度的CMAPSO算法

李成严，宋月，马金涛

摘要：針对多目标云资源调度问题，以优化任务的总完成时间和总执行成本为目标，采用模糊数学的方法，建立了模糊云资源调度模型。利用协方差矩阵能够解决非凸性问题的优势，采取协方差进化策略对种群进行初始化，并提出了一种混合智能优化算法CMAPSO算法（covariance matrix adaptation evolution strategy particle swarm optimization，CMAPSO ），并使用该算法对模糊云资源调度模型进行求解。使用Cloudsim仿真平台随机生成云计算资源调度的数据，对CMAPSO算法进行测试，实验结果证明了CMAPSO算法对比PSO算法（particle wwarm optimization），在寻优能力方面提升28%，迭代次数相比提升20%，并且具有良好的负载均衡性能。

关键词：云计算;任务调度;粒子群算法; 协方差矩阵进化策略

DOI：10.15938/j.jhust.2022.01.005

中图分类号： TP399    文献标志码： A    文章编号： 1007-2683（2022）01-0031-09

CMAPSO Algorithm for Fuzzy Cloud Resource Scheduling

LI Chengyan，SONG Yue，MA Jintao

（School of Computer Science and Technology， Harbin University of Science and Technology， Harbin 150080，China）

Abstract：Aiming at the multiobjective cloud resource scheduling problem， with the goal of optimizing the total completion time and total execution cost of the task， a fuzzy cloud resource scheduling model is established using the method of fuzzy mathematics. Utilizing the advantage of the covariance matrix that can solve the nonconvexity problem， adopting the covariance evolution strategy to initialize the population， a hybrid intelligent optimization algorithm CMAPSO algorithm （covariance matrix adaptation evolution strategy particle swarm optimization，CMAPSO） is proposed to solve the fuzzy cloud resource scheduling model. The Cloudsim simulation platform was used to randomly generate cloud computing resource scheduling data， and the CMAPSO algorithm was tested. The experimental results showed that compared with the PSO algorithm （particle swarm optimization）， the optimization capability of CMAPSO algorithm is increased by 28%， the number of iterations of CMAPSO algorithm is increased by 20%， and it has good load balancing performance.

Keywords：cloud computing; task scheduling; particle swarm algorithm; covariance matrix adaptation evolution strategy

0引言

云计算是一种商业计算的模型和服务模式[1]，而云计算资源调度的主要目的是将网络上的资源进行统一的管理和调式，再给予用户服务调用。如何将计算资源和数据进行有效的管理和使用，就是云计算资源调度的主要研究目标。

云资源调度问题是一个NP难问题，有效的资源调度可以降低任务的执行时间，减少执行成本和能源消耗等，并能对可靠性，安全性，可用性和可伸缩性等QoS需求进行考虑。如果使用现有的调度方法，比如说时间片轮转，先进先出算法，哈希法，贪心算法等，很难达到使云计算资源调度的各个方面都满意的地步，会产生服务性能失衡，或者其他的一些问题[2]。

现阶段，对于智能算法的研究是解决云计算资源调度问题的主要研究方向。诸如粒子群算法（particle swarm optimization， PSO）[3]，蚁群算法（ant colony optimization， ACO）[4]，遗传算法（genetic algorithm， GA）[5]，模拟退火算法（simulated annealing， SA）[6]等。PSO算法具有可调参数少，收敛速度快的优点，而且PSO算法在搜索过程中，会将当前的全局最优和局部最优都进行“记忆”，这有益于粒子群在之后的寻优搜索。但是粒子群算法使用的是随机初始化的方式，这就可能导致粒子在解空间中可能存在分布不均匀或者粒子的拟合度过高的问题，不利于粒子种群的寻优。

协方差矩阵自适应进化策略[7]（covariance matrix adaptation evolution strategy， CAMES ）是一种以进化策略为基础发展起来的，对于解决非线性问题具有良好适应性的算法。本文利用CMAES的协方差矩阵具有的高引导性的性能[8]，提升PSO算法在初始化阶段存在的不足。通过协方差矩阵进化生成高质量的解集[9]，使用该解集对PSO算法进行初始化，改变原有的初始化方式，使粒子在初始阶段就具有分布均匀且离最优解较近的优势。所以本文提出一种基于协方差矩阵的粒子群优化算法，CMAPSO算法（covariance matrix adaptation evolution strategy particle swarm optimization， CMAPSO ）对模糊云计算资源调度问题进行求解。

本文的结构如下，第一部分对模糊云计算资源

问题的模型进行描述，第二部分对CMAPSO算法进行描述，第三部分在仿真平台上进行实验，第四部分对实验结果进行总结分析并给出结论。

1模糊云资源调度模型

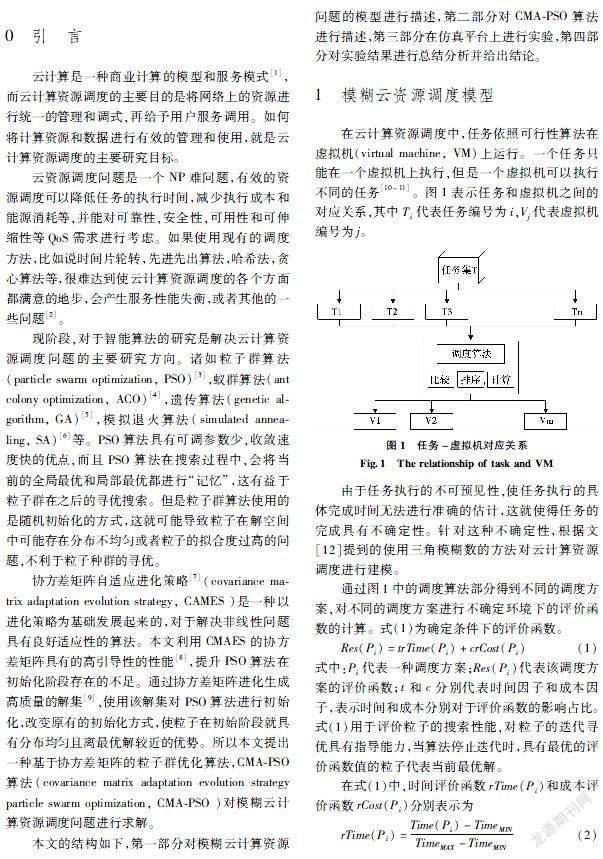
在云计算资源调度中，任务依照可行性算法在虚拟机（virtual machine， VM）上运行。一个任务只能在一个虚拟机上执行，但是一个虚拟机可以执行不同的任务[10-11]。图1表示任务和虚拟机之间的对应关系，其中Ti代表任务编号为i，Vj代表虚拟机编号为j。

由于任务执行的不可预见性，使任务执行的具体完成时间无法进行准确的估计，这就使得任务的完成具有不确定性。针对这种不确定性，根据文[12]提到的使用三角模糊数的方法对云计算资源调度进行建模。

通过图1中的调度算法部分得到不同的调度方案，对不同的调度方案进行不确定环境下的评价函数的计算。式（1）为确定条件下的评价函数。

Res（Pi）=trTime（Pi）+crCost（Pi）（1）

式中：Pi代表一种调度方案;Res（Pi）代表该调度方案的评价函数;t和c分别代表时间因子和成本因子，表示时间和成本分別对于评价函数的影响占比。式（1）用于评价粒子的搜索性能，对粒子的迭代寻优具有指导能力，当算法停止迭代时，具有最优的评价函数值的粒子代表当前最优解。

在式（1）中，时间评价函数rTime（Pi）和成本评价函数rCost（Pi）分别表示为

rTime（Pi）=Time（Pi）-TimeMINTimeMAX-TimeMIN（2）

rCost（Pi）=Cost（Pi）-CostMINCostMAX-CostMIN（3）

式中：TimeMAX和TimeMIN分别代表任务在虚拟机上执行的最长时间和最短时间; CostMAX和CostMIN分别代表任务执行所需的最大成本和最小成本。

调度方案P总的执行时间计算公式为

Time（Pi）=maxmj=1vmTime（4）

vmTimej表示第j个虚拟机的执行时间。

调度方案P总的执行成本计算公式为

Cost（Pi）=∑mj=1vmTimej×cstj（5）

式中：cstj表示第j个虚拟机单位时间内的执行成本。

根据三角模糊数的特性，通过隶属函数对任务的执行时间进行表示。

μT（x）=x-tLtM-tL，x∈[tL，tM]

tR-xtR-tM，x∈[tM，tR]（6）

当x≤tL，x≥tR时μT（x）=0。其中tL，tR分别表示任务可能的最短执行时间和最长执行时间;tM表示任务最可能的执行时间。tL，tR根据式（7）和式（8）进行计算：

tL=tM×（l+（1-l）×Rand（））（7）

tR=tM×（1+（u-1）×Rand（））（8）

式中l和u代表模糊下界和模糊上界的系数，Rand（）代表随机生成数，范围在[0，1]之间。根据三角模糊数的线性特性和可分解性，不确定的云计算资源调度模型中的评价函数表示为

min{res（Pi）}=min{P～}=min{PL，PM，PR}（9）

根据三角模糊数的隶属函数将式（1）转换为模糊模型进行求解。根据可分解性，在式（9）中，模糊之后的评价函数的3个端点PL，PM，PR与模糊执行时间的3个端点tL，tM，tR有关。

x-p（X～）=14（XL+2XM+XR）（10）

σp（X～）=180[3（XL）2+4（XM）2+3（XR）2-

4XLXM-2XLXR-4XMXR]12（11）

式（10）是对模糊数取平均值，公式（11）是对模糊数取标准差，二者都是对模糊数进行去模糊化处理。使用文[13]中提到的对模糊数进行排序的方法，对评价函数进行均值和方差的计算，如果该评价函数的模糊数的平均值较高，方差较低，那么认为该评价函数对应的调度方案越好。

根据该排序方式，将式（9）去模糊化之后转变为式（12）：

min{res（Pi）}=min{P～}=min{PL，PM，PR}=

min{Pη+Pμ}（12）

其中表示对不确定度的加权系数。

负载均衡的计算公式为

Load=min1≤i≤mvmTimeimax1≤i≤mvmTimei（13）

其中：min1≤i≤mvmTimei代表虚拟机执行最短时间;max1≤i≤mvmTimei代表虚拟机最长执行时间。对于负载均衡度来说，负载越接近于1，说明负载越均衡，当负载均衡度为0时，说明有的虚拟机没有被分配到任务，这时负载均衡性较差。负载均衡也是本文衡量算法是否具有稳定性的一个指标。

2CMAPSO算法

2.1算法思想

PSO算法在寻优过程中，由于问题的非凸性的本质，可能会陷入局部最优状态，如果使用随机初始化的方式，可能会因为初始解的分布不均，拟合度过高等问题，导致算法搜索不到最优解。而CMAPSO算法利用协方差矩阵的健壮性，对搜索空间映射的不变性等特点，能够有效的解决具有非凸性的目标函数的问题[14]。

利用这种优势，本文提出的CMAPSO算法利用协方差矩阵进化过程中，产生的采样个体逐渐靠近最优解的特点，对采样个体进行存储，产生种群的初始矩阵A。使得CMAPSO算法在初始阶段就具有离最优解较近的初始值，且均匀分布在最优解的周围。这就使得CMAPSO算法在初始搜索阶段，就能够对最优解所在区域进行精细搜索，提升搜索精度[15，16]。

下面对CMAPSO算法求解模糊云计算资源调度问题的步骤进行详细描述。

2.2种群初始化

协方差矩阵自适应进化策略是依靠多维协方差矩阵自适应调整，使其逐步逼近Hessian矩阵，从而收敛得到最优解。根据這一特性，本文通过协方差矩阵得到CMAPSO算法的初始矩阵，并对粒子种群进行初始化。

协方差矩阵C服从多维正态分布N（m，C），并且C表示种群的突变方向和突变尺度，通过当前的最优解rgrgx与前一代的平均值m的关系更新协方差矩阵C，使整个种群向着最优解的方向进行突变。协方差矩阵C的规模为N×N，其中N=TaskNum+VmNum，TaskNum为云计算资源调度中任务的规模，VmNum为虚拟机的规模，VmNum小于TaskNum。

使用协方差自适应进化策略求解云资源调度问题，主要需要对协方差矩阵C进行初始化，初始矩阵C=I∈RN×N，然后根据该初始协方差矩阵更新逐步对搜索种群进行更新，得到搜索种群rgrgx，根据该搜索种群获取任务对应的虚拟机编号。然后根据该搜索种群可以对协方差矩阵C进行迭代更新，重复上述步骤，找到最优的调度方案。

在CMAPSO算法中，设置子代大小为λ，父代大小为μ（λ<μ），g代表当前迭代次数，pathgσ∈RN，pathgc∈RN，σg∈R+，其中path0σ=path0c=0。

根据公式（14）生成CMAPSO算法的搜索种群rgrgx。

rgrgxg+1k=m+σgBgDgN（0，I）～N（m，σ2C）（14）

其中：rgrgxg+1k代表第g+1次迭代的第k个个体;m代表群体均值，m=∑μi=1ωirgrgxi：λ（其中∑μi=1ωi=1）;B矩阵的列向量是协方差矩阵C的特征向量正交基;D的对角元素是由特征向量C的特征值的平方根构成的对角阵。

通过式（15）计算进化路径pathσ。利用进化路径对进化步长进行累积控制。

pathσ=（1-cσ）pathσ+cσ（2-cσ）μeffC-12×

∑μi=1[ωi（rgrgxi-m）/σ]（15）

其中：μeff=1/∑μi=1ω2i表示协方差矩阵的有效选择质量;cσ表示对前一代的pathσ的学习率。

全局步长的更新公式为

σ=σexpcσdσ||pathσ||E||N（0，I）||-1（16）

其中：dσ代表阻尼系数且dσ≈1，E||N（0，I）||代表多维正态分布范数的期望值。

式（17）对协方差矩阵进化路径pathc进行计算。根据pathc对协方差矩阵进行调整。

pathc=（1-cc）pathc+hccc（2-cc）μeff×

∑μi=1[ωi（rgrgxi-m）/σ]（17）

其中：hσ代表Heaviside函数;控制协方差矩阵在线性环境中的增长速度;cc表示对前一代的pathc的学习率。

对于协方差矩阵的更新公式为

C=（1-c1-cμ）C+c1（pathcpathTc+δ（hσ）C）+

cμ∑μi=1[ωi（（rgrgxi-m）/σ）（（rgrgxi-m）/σ）T]（18）

其中δ（hσ）=（1-hσ）cc（2-cc）;c1，cμ表示秩为1和秩为μ的协方差矩阵C的学习更新率。

根据式（14）获得搜索种群rgrgx，根据式（14），（15），（16），（17）获得式（18）中对应参数，对协方差矩阵C进行更新，根据更新后的矩阵重新获取搜索种群rgrgx，得到相应的调度方案。

根据协方差矩阵生成初始矩阵的算法描述，设置采样个体的维数设置为N，计算采样种群rgrgx的数值，然后进行排序比较，在父代μ中截取子代λ大小，对此时数值较小的rgrgx的行进行记录，即为虚拟机的编号，列代表的就是任务号。

例如，如果有编号0到9共10个任务，编号0到3共4个虚拟机，min（xij），其中j∈（0，3），i∈（0，9），代表第j个任务在第i号虚拟机上执行。

将每一次迭代产生采样个体表示的任务和虚拟机的对应关系依次存储在矩阵A中，就得到了CMAPSO算法的初始种群。

2.3寻优迭代

根据2.2节产生的初始矩阵A对CMAPSO算法进行初始化，能够得到在解空间中离最优解较近且分布均匀的解集，然后通过这个解集对CMAPSO算法进行之后的迭代寻优操作，使CMAPSO算法能够较快收敛到质量更高的解。

CMAPSO算法通过粒子群的速度和位移的变换，经过多次的迭代搜索，使“粒子”向着个体最优pBest（自身经历）和全局最优gBest（社会经历）的方向进行移动。

粒子的速度更新公式为

Vg+1=ωVg+c1rand（）（pBest-rgrgxg）+

c2rand（）（gBest-rgrgxg）（19）

粒子的位移更新公式为

rgrgxg+1=rgrgxg+Vg+1（20）

在速度更新公式中，ω为惯性因子，当它的值较大时，全局搜索能力强，当它的值较小时，局部搜索能力强。c1为个体学习因子，表示对自身最优解的学习能力，c2为群体学习因子，表示对当前全局最优解的学习能力。rand（）表示（0，1）之间的随机数。

在CMAPSO算法求解模糊云计算资源调度问题时，式（20）中每一个粒子的位移代表一种调度方案，通过比较相应的评价函数值，对粒子的速度和位移进行更新。其中粒子的维度代表任务集的大小，每一维代表一个任务，每一维的取值代表该任务在哪一个虚拟机上执行。

图2对粒子与任务和虚拟机的关系进行了举例。

其中，0，1，2，3…，n代表n个任务，下面的3，1，m，0，…，2，代表每个任务在那一台虚拟机上执行。比如0号任务在3号虚拟机上执行，1号任务在1号虚拟机上执行，以此类推，得到一個粒子表示的任务和虚拟机的映射关系，即为一个调度方案。

CMAPSO算法求解模糊云计算调度模型时，使用评价函数对得到的调度方案进行比较，然后进行下一步的迭代搜索，直到找到最优的解。

2.4CMAPSO算法流程与时间复杂度

在CMAPSO算法中，主要包括使用协方差矩阵生成矩阵A对粒子种群进行初始化，CMAPSO算法的迭代寻优操作等。

使用矩阵A对粒子种群进行初始化，要考虑生成初始矩阵A时的时间复杂度。在生成初始矩阵A时，需要进行三种函数的计算，分别为更新采样种群，更新搜索步长，更新协方差矩阵，而每一种函数的计算最坏的时间复杂度均为O（N3），所以生成CMAPSO算法的初始矩阵A的最坏时间复杂度为O（g×3N3），其中g为迭代次数，N为协方差矩阵C的行数。

CMAPSO算法在求解云计算资源调度问题时，迭代过程的最坏时间复杂度为O（taskNum×popsize×g），其中popsize代表粒子种群的大小。

算法中的其他操作，比如评价函数值的比较等操作，时间复杂度较小，与上述过程相比较，可以忽略不计。

综上所述，本文提出的CMAPSO算法的时间复杂度为

T（n）=O（g×3N3）+O（taskNum×popsize×g）=

O（g×3N3）（21）

CMAPSO算法的流程图如图3所示。

3仿真实验

3.1数据生成与参数选择

为了验证本文提出的CMAPSO算法在求解模糊云计算资源调度方面的准确性，使用云计算仿真平台Cloudsim进行仿真实验。使用文[17]的方法，生成任务集，每个任务的大小范围为[3000，130000]，生成虚拟机集，虚拟机的执行速度范围为[300，1300]。根据任务的大小和虚拟机的执行速度计算任务在不同虚拟机上的执行时间。根据虚拟机的处理调度根据规则计算得出单位时间内虚拟机的执行成本。

经过大量的反复实验，在过程中发现CMAPSO算法在迭代100左右时，能够过得比较稳定的解，所以将算法的迭代次数设置为100任务的规模分别为50，100，150。虚拟机的个数设置为5。

表1为实验过程中的参数设置。表2为实验过程中算法的参数设置。

在表2中个体学习因子和全体学习因子都设置为0.5，表示对当前代的个体最优和群体最优的学习能力相同，时间因子t和成本因子c都设置为0.5，表示在求解评价函数时，对于时间和成本的考虑相同。

在实验过程中，除了解决云计算资源调度问题的算法不同之外，实验参数和实验环境均相同。

3.2数值实例

在本文中，为了验证本文使用CMAPSO算法在初始阶段就具有距离最优解较近的优势，使用下述实例进行验证。

例如，在云计算资源调度中有任务数为10，虚拟机数为3时，使用随机和初始矩阵A对粒子t和h分别进行初始化，对得到的调度方案使用式（9）进行评价。在实验中，随机初始化粒子t，得到粒子的位置为rgrgxt{0，0，1，2，2，0，0，0，0，1}，此时它的评价函数为Res（P（t））=0.4112119。使用式（19）和式（20）对粒子t的速度和位置进行迭代更新，继续对解空间进行搜索，得到的粒子的位置为rgrgxt{1，0，0，2，1，0，2，0，1，0}，此时的评价函数为Res（P（t））=0.3786563。通过2.1节种群初始化获得的初始矩阵A对粒子h进行初始化，得到其一个粒子h的位置为rgrgxh{2，2，1，0，1，0，0，2，0，1}，此时它的评价函数为Res（P（h））=0.2942045。根据式（19）和式（20）对粒子h的速度和位置进行迭代更新，继续对解空间进行搜索，得到最终解为rgrgxh{1，2，0，1，1，2，0，0，2，1}，此时的评价函数为Res（P（h））=0.2763707。通过上述实例可以看出，使用CMAPSO算法得到的调度方案的评价函数值较小，而使用随机初始化得到调度方案的评价函数值较大，粒子h相比于粒子t最终得到调度方案优越性提升了约28%，并且在实验过程中发现CMAPSO算法的迭代次数相比提升了约20%。

通过该数值实例，可以了解本文提出的CMAPSO算法，并且对于该算法提出的必要性进行了论证。

3.3算法性能分析

在本文中，为了验证本文算法的性能，使用反向世代距离[18]（inverted generational distance， IGD），超体积[19]（hypervolume， HV），准确性度量指标覆盖率[20]（converage metric， CMetric）对CMAPSO算法，与NSGA算法[21]，NSGAⅡ算法[22]，NSGAⅢ算法[23]和MOEA/D算法[24]的性能进行量化。表3所示为5种算法的性能对比结果。结果均使用平均值表示。

从表中的IGD值来看，算法CMAPSO具有最小的IGD值，说明CMAPSO得到的解的分布更加均匀。算法CMAPSO有最高的HV值，这也说明它得到的解的质量更高。由于初始就获得了高质量的集合，从CMetric值可以看出，CMAPSO算法求得的解的收敛性也较优。综上，本文提出的CMAPSO算法能够获得较好的调度方案。

3.4模型对比

为了验证本文提出的针对不确定云资源调度模型的准确性和实际性能，使用不同的任务规模，相同虚拟机规模对确定云计算资源调度模型和不确定云

计算资源调度模型进行实验对比分析。图4为两种模型的评价函数对比。横坐标为任务数，纵坐标为评价函数值。虚拟机数量均为5。

从图4可以看出，不论任务规模多大，不确定云计算资源调度的评价函数值都比确定云计算资源调度的评价函数值高，这正是因为任务执行的不确定性导致的，所以在实验过程中需要考虑这种不确定性的存在。

3.5算法寻优能力对比

为了验证本文提出的CMAPSO算法具有良好的寻优性能，本文采用相同数据集，相同环境下的协方差矩阵自适应进化策略算法和PSO算法与它进行对比分析。根据评价函数的取值来判定寻优性能的好坏，算法的评价函数值越低，认为该算法的寻优性能越好。

图5～7表示在任务数和虚拟机数分别为（50，5），（100，5），（150，5）时PSO算法，协方差矩阵自适应进化策略和CMAPSO算法的寻优能力对比图。横坐标代表算法的迭代次数，纵坐标代表对应的评价函数值。

从图中可以看出，无论任务规模的大小，CMAPSO算法在解决云计算资源调度问题时，相比于其他两种算法都有较好的寻优性能。在图中还可以看出，CMAPSO算法由于在初始搜索阶段就具有质量较高的解，所以初始搜索性能就高于其他两种算法。而且由于这种优势，使得CMAPSO算法收敛到最优解的迭代次数最少，收敛速度较快。

本文使用权重占比的方式对评价函数中时间和成本进行比重控制，当时间因子和成本因子均为0.5时，分别对PSO算法，CMAES算法，CMAPSO算法任务执行总时间和总成本进行记录，执行任务的虚拟机个数均为5，实验结果如图8，图9所示。图中横坐标均表示任务数量，图8中纵坐标代表执行总时间，图9中纵坐标代表执行总成本。

从图8和图9中可以看出，使用3种算法对同一个数据集的任务执行总时间和总成本进行记录，可以看出本文提出的CMAPSO算法求解双目标下的资源调度方案能够使任务总的执行时间最短，总执行成本最低。

图10表示3种算法间的负载均衡对比图，横坐标表示算法在求解云计算资源调度时的任务规模与虚拟机规模，纵坐标表示算法的负载均衡能力。

通过上述实验对比可知，CMAPSO算法在解决模糊云计算资源调度时，不仅具有较好的寻优性能，而且算法的收敛速度也是较快的，在负载均衡方面，也能够减轻虚拟机的工作压力。可以看出，CMAPSO算法在整体上具有良好的性能。

4结语

本文的主要目标是降低任务总的完成时间和执行成本，对模糊云计算资源调度模型进行求解。本文使用了一种混合优化算法CMAPSO算法，结合协方差矩阵自适应进化策略和PSO算法的优势，使该算法的寻优能力较好，并且寻优速度较快，该算法还能够提高负载均衡性能，使对资源的利用率提高。实验证明了CMAPSO算法能够提高云计算资源调度的整体性能。

參 考 文 献：

[1]SINGH S， CHANA I. A Survey on Resource Scheduling in Cloud Computing： Issues and Challenges[J]. Journal of Grid Computing， 2016， 14（2）：217.

[2]张雨， 李芳， 周涛. 云计算环境下基于遗传蚁群算法的任务调度研究[J]. 计算机工程与应用， 2014， 50（6）：51.

ZHANG Yu， LI Fang， ZHOU Tao. Task Scheduling Algorithm Based on Genetic Ant Colony Algorithm in Cloud Computing Environment[J]. Computer Engineering and Applications， 2014， 50（6）：51.

[3]SADHASIVAM N， THANGARAJ P. Design of an Improved PSO Algorithm for Workflow Scheduling in Cloud Computing Environment[J]. Intelligent Automation & Soft Computing， 2016，31（8）：493.

[4]HU X X， ZHOU X W. Improved Ant Colony Algorithm on Scheduling Optimization of Cloud Computing Resources[J]. Applied Mechanics & Materials， 2014， 678：75.

[5]HASSAN M A， KACEM I， MARTIN S， et al. Genetic Algorithms for Job Scheduling in Cloud Computing[J]. Studies in Informatics & Control， 2015， 24（4）：387.

[6]CUNHA M， MARQUES J. A New Multiobjective Simulated Annealing Algorithm—MOSAGR： Application to the Optimal Design of Water Distribution Networks[J]. Water Resources Research， 2020， 56（3）：e2019WR025852.

[7]陈兴国，徐修颖，陈康扬，等. 基于CMAES集成学习方法的地表水质分类[J]. 计算机科学与探索，2020（3）： 426.

CHEN Xingguo， XU Xiuying， CHEN Kangyang，et al. SurfaceWater Quality Classification via CMAES Ensemble Method[J]. Journal of Frontiers of Computer Science and Technology， 2020（3）： 426.

[8]黄亚飞， 梁昔明， 陈义雄. 求解全局优化问题的正交协方差矩阵自适应进化策略算法[J]. 计算机应用， 2012（4）：95.

HUANG Yafei， LIANG Ximing， CHEN Yixiong. Hybrid Orthogonal CMAES for Solving Global Optimization Problems[J]. journal of Computer Applications， 2012（4）：95.

[9]饶华， 王忠， 李欣. 基于CMAESSVR的WLAN室内定位算法研究[J]. 计算机应用研究， 2019， 36（8）：2514.

RAO Hua， WANG Zhong， LI Xin. Research on WLAN Indoor Positioning Algorithm Based on CMAESSVR[J]. Application Research of Computers， 2019， 36（8）：2514.

[10]王恩重， 陶传奇. 基于改进蚁群优化算法的云计算调度方法[J]. 计算机与数字工程， 2019， 47（4）.

WANG Enzhong， TAO Chuanqi. Cloud Computing Scheduling Method Based on Improved Ant Colony Optimization Algorithm[J]. Computer & Digital Engineering， 2019， 47（4）.

[11]朱亚会， 陳丹， 庄毅. 云数据中心资源利用率均衡的虚拟机调度算法[J]. 小型微型计算机系统， 2017（2）：232.

ZHU Yahui， CHEN Dan， ZHUANG Yi. Virtual Machine Scheduling Algorithm for Resource Utilization Balanced in Cloud Data Center[J]. Minimicro Systems， 2017（2）：232.

[12]李成严， 曹克翰， 冯世祥，等. 不确定执行时间的云计算资源调度[J]. 哈尔滨理工大学学报， 2019， 24（1）：89.

LI Chengyan， CAO Kehan， FENG Shixiang， et al. Resource Scheduling with Uncertain Execution Time in Cloud Computing[J]. Journal of Harbin University of Science and Technology， 2019， 24（1）：89.

[13]BALIN， SAVAS. Nonidentical Parallel Machine Scheduling with Fuzzy Processing Times Using Genetic Algorithm and Simulation[J]. International Journal of Advanced Manufacturing Technology， 2012， 61（9/12）： 1115.

[14]NIKOLAUS Hansen. The CMA Evolution Strategy： A Comparing Review[M]. Berlin：Springer， Towards a New Evolutionary Computation， 2006.

[15]邓志诚，孙辉，赵嘉，等.具有动态子空间的随机单维变异粒子群算法[J].计算机科学与探索， 2020，14（8）：1409.

DENG Zhicheng， SUN Hui， ZHAO Jia，et al. Stochastic SingleDimensional Mutated Particle Swarm Optimization with Dynamic Subspace[J]. Journal of Frontiers of Computer Science and Technology，2020，14（8）：1409.

[16]HANSEN N， OSTERMEIER A. Completely Derandomized SelfAdaptation in Evolution Strategies[J].Evolutionary Computation， 2001，9（2）：159.

[17]CALHEIROS R N， RANJAN R， BELOGLAZOV A， et al. CloudSim： a Toolkit for Modeling and Simulation of Cloud Computing Environments and Evaluation of Resource Provisioning Algorithms[J]. Software Practice & Experience， 2010， 41（1）：23.

[18]MARGARITA Reyes Sierra， CARLOS Coello A. Coello. Improving PSOBased Multiobjective Optimization Using Crowding， Mutation and∈Dominance[C]// International Conference on Evolutionary MultiCriterion Optimization. Springer， Berlin， Heidelberg， 2005： 505.

[19]SCHTZE， Oliver， Hernández， Víctor Adrián Sosa， Trautmann H， et al. The Hypervolume Based Directed Search Method for Multiobjective Optimization Problems[J]. Journal of Heurs， 2016， 22（3）：1.

[20]LIU R C， LI J X， LIU J， et al. A Survey on Dynamic MultiObjective Optimization[J]. Chinese Journal of Computers， 2020，43（7）：1246.

[21]ZHENG J H， SHI Z Z， XIE Y. A Fast Multiobjective Genetic Algorithm Based on Clustering[J]. Journal of Computer Research and Development， 2004（7）：44.

[22]SAHMOUD S， TOPCUOGLU H R. Sensorbased Changedetection Schemes for Dynamic Multiobjective Optimization Problems[C]// 2016 IEEE Symposium Series on Computational Intelligence （SSCI）， 2016：1.

[23]MIRIAM A J， SAMINATHAN R， CHAKARAVARTHI S. Nondominated Sorting Genetic Algorithm （NSGAIII） for Effective Resource Allocation in Cloud[J]. Evolutionary Intelligence， 2020（2）：436.

[24]LI H， ZHANG Q F. MOEA/D： a Multiobjective Evolutionary Algorithm Based on Decomposition[J]. IEEE Trans on Evolutionary Computation， 2007， 11（6）： 712.

（編辑：温泽宇）