公路模板支架工程施工安全指标体系构建及权重等级划分
冯晓楠, 李加朋, 张建东,3, 刘 朵
(1.苏交科集团股份有限公司, 南京 211112; 2.河海大学 土木与工程学院, 南京 210098;3.在役长大桥梁安全与健康国家重点实验室, 南京 211112)
模架工程是一种非常重要的临时支撑和辅助设施结构,广泛用于现浇混凝土结构施工中[1-2]。在现有规范和管理文件中,针对模架工程的施工安全指标缺乏系统性的规定,致使安全管理人员无法有效开展相应的安全检查与管理工作。同时,现场施工人员对模架工程安全施工的重要性认识不足,致使现场施工中存在大量安全隐患问题,包括人的不安全行为和物的不安全状态[3]。这些问题导致了模架工程施工安全事故频发且难以控制。因此,有必要建立完善的模架工程施工安全指标体系,并明确其指标的重要性等级,这不仅可为模架工程施工安全事故预防及管理工作提供技术依据,还对公路工程现场施工安全管理具有重要指导作用。
模架工程施工安全技术指标体系是指由若干个反映模架工程施工安全状态的相对独立又相互联系的技术指标所组成的有机整体。针对模架工程,已有研究学者[4-6]开展了大量的调研、理论及试验研究,提出了相应的设计计算方法、安全管理措施等,但大部分局限于结构本身的可靠性和安全性,缺乏相应的安全技术指标体系研究。模架工程施工安全技术指标包括人、物、环、管等多方面因素,且在模架工程施工过程中,各个安全技术指标超出标准要求的概率及产生的事故后果也存在较大差异。因此,急需针对各安全技术指标进行重要性程度等级划分,为交通建设行业安全施工提供可靠、适用的参考系和风向标。
鉴于此,笔者将通过模架工程典型安全事故及现有安全规范调研分析,筛选与施工安全相关的技术指标,建立模架工程施工安全技术指标体系,根据德尔菲法和基于三角模糊数的层次分析法,确立安全技术指标的重要性权重值,并进行安全技术指标重要性等级划分,为更好地预防模架工程施工安全事故的发生和提高其施工安全管理水平提供技术支撑。
1 施工安全技术指标筛选
根据相关规范[7]中安全事故的定义,针对近30起模架工程施工安全事故进行致因分析,主要包括安全事故的类型、事故发生的形式以及事故发生的原因,结果见表1。分析发现,模架工程在施工过程中常发生的安全事故类型包括:高处坠落、坍塌、物体打击等;发生的原因一般包括人的不安全行为、物的不安全状态、环境的不安全性及管理措施的缺陷等四大因素。针对每个事故原因提取其涉及的安全技术指标,由于篇幅原因在此不再一一赘述。
我国与施工安全相关的规范标准、管理文件约有50多部,主要规范见表2,但明确提出施工安全技术指标的规范标准较少,仅在危险源辨识及安全检查评价中提出了部分施工安全技术指标。
综合模架工程安全事故与现有规范标准调研分析结果,统计筛选出模架工程施工安全技术指标共有64项,见表3。

表1 模架工程施工事故分析(示例)

表2 主要参考的规范标准清单

表3 模架工程施工安全技术指标

表3(续)

表3(续)
2 构建指标体系
模架工程施工安全技术指标体系的构建应遵守目的性、系统性、独立性、科学性、定性与定量指标相结合等原则[8]。采用层次分析法,将模架工程施工安全问题进一步细分,划分成多个相互联系的组成要素,从而构建一个有序的递阶层次结构,使整个模架工程安全问题概念化、条理化、层次化。这一递阶层次结构由目标层、因素层和指标层构成[9],如图1所示。
1) 目标层。即本体系的目的,建立模架工程施工安全技术指标体系。
2) 因素层。指影响模架工程施工安全的因素,主要有“人的因素”“物的因素”“环境因素”和“管理因素”。
3) 指标层。将各因素进一步细化形成指标,并提出相应的定量与定性控制标准。
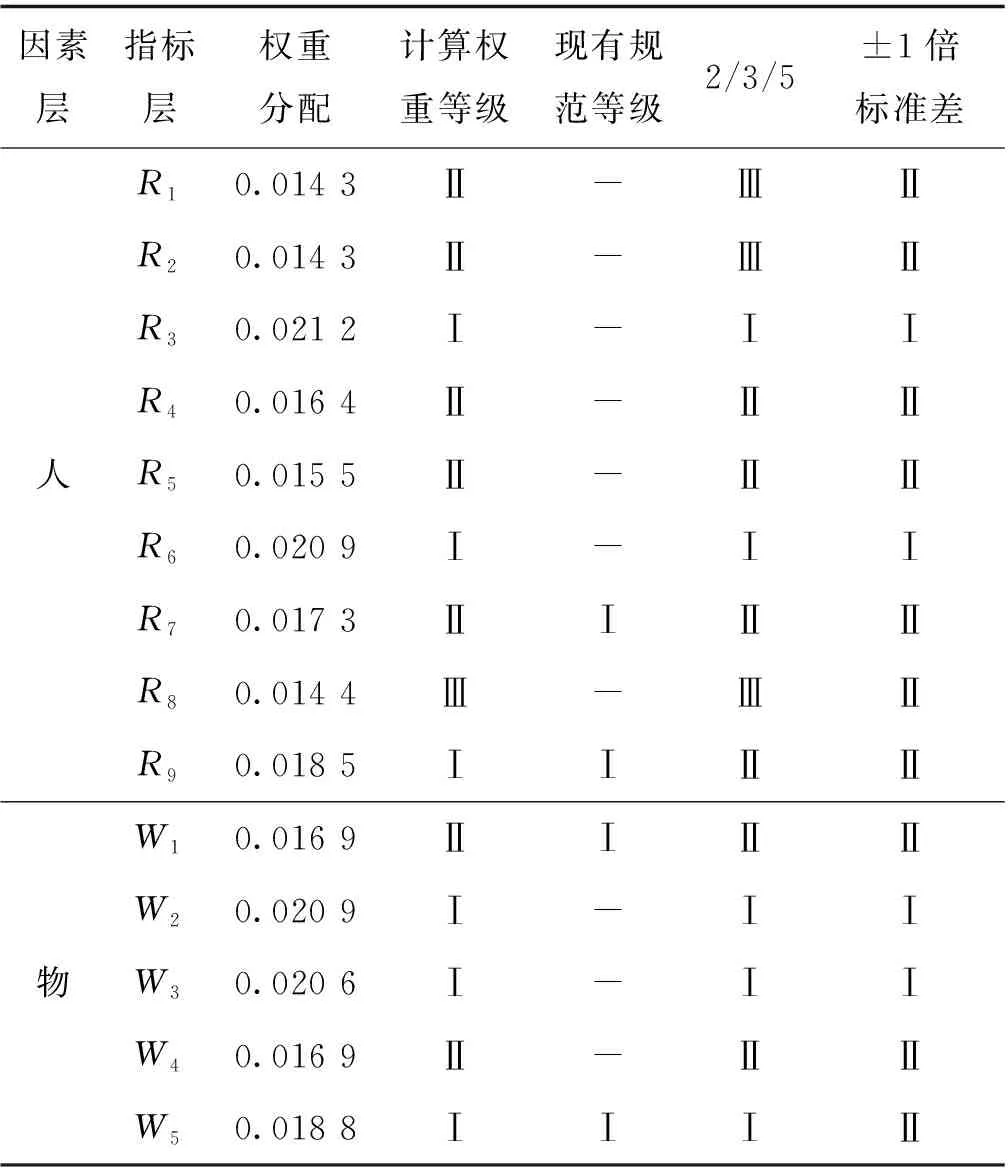
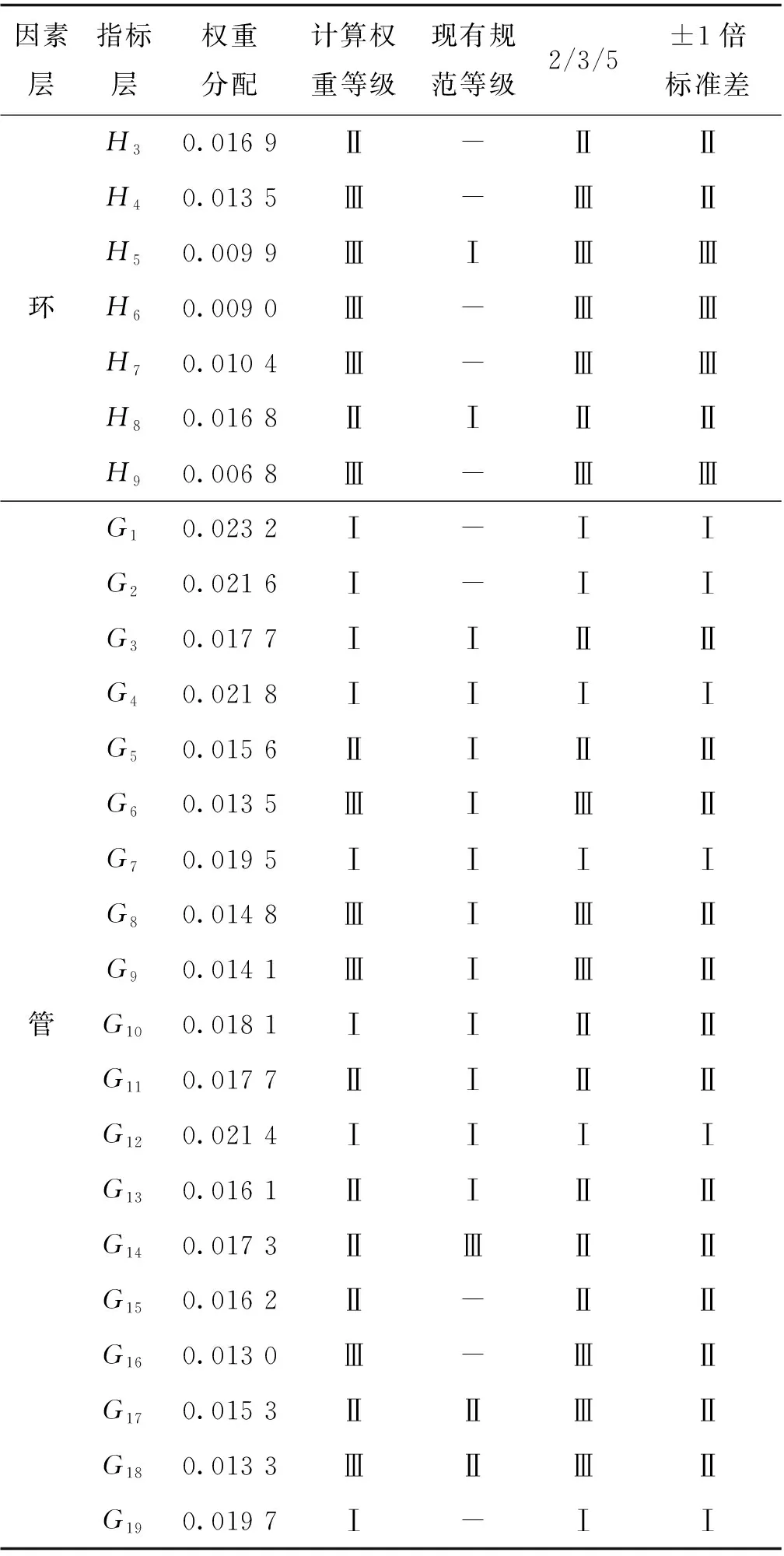
根据以上方法,构建模架工程施工安全技术指标体系,“人-物-环-管”各因素分别包含有R1~R9、W1~W27、H1~H9、G1~G19安全技术指标,见表3。
3 安全技术指标等级划分
借鉴现有工程安全风险评估方法,利用菲尔德
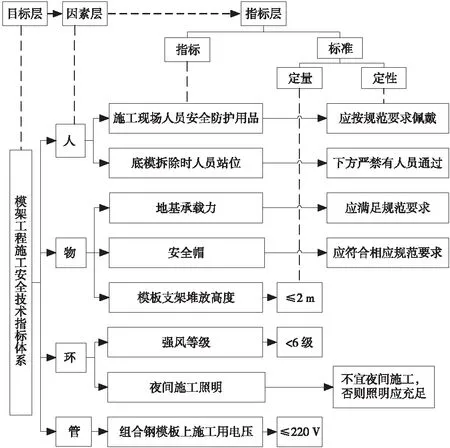
图1 模架工程施工安全技术指标体系
法和基于三角模糊数的层次分析法,实现对模架工程施工安全技术指标的权重等级划分,流程如图2所示。

图2 安全技术指标的权重等级划分流程
3.1 指标重要性程度调研
模架工程安全技术指标共有64个,若直接采用三角模糊数层次分析法[10-11]中对各指标两两比较的方法,将给打分专家造成较大麻烦,会增加调研结果的不可靠性。因此,为方便专家打分,只根据重要性程度针对每个指标打1~9分,打分标准见表4。为保证调研结果的合理性及科学性,共调研11家单位20位专家。

表4 指标重要性程度专家打分标准
3.2 确定指标权重值计算
1) 构建判断矩阵
根据三角模糊数的层次分析法基本原理[12-13],首先需要构建判断矩阵,由于每个专家打分方法并不是按1~9标度法进行比较,因此,需要将专家打分结果转化为1~9标度法。具体转化方法见公式(1)、(2)。
Ci/Cj=(cik-cjk)+1cik≥cjk
(1)
Cj/Ci=1/[(cjk-cik)+1]cik (2) 式中:cik为第k个专家对Ci指标的打分值;cjk为第k个专家对Cj指标的打分值。 2) 构建三角模糊数判断矩阵 将20位打分专家对64个安全技术指标的相对重要性判断结果用三角模糊数公式(3)~(6)表示,并形成三角模糊数判断矩阵,结果见表5。 (3) lij=min(Bijk) (4) (5) uij=max(Bijk) (6) 3) 去模糊化 去模糊化的方法有很多种,其中一种较容易操作的去模糊方法,其判断如公式(7)~(9)所示。 0≤α≤1 0≤λ≤1 (7) lijα=(mij-lij)×α+lij (8) uijα=uij-(uij-mij)×α (9) 表5 三角模糊数判断矩阵 式中:α是决策者的偏好系数,α的大小反映了判断的不确定性。当α=0时,不确定性最大;当α=1时,几乎没有不确定性。λ的取值取决于决策者对风险的态度。当λ=0.5时,决策者是风险中立的;当λ<0.5时,决策者是追求风险的;当λ>0.5时,决策者是厌恶风险的。 采用此方法将三角模糊数判断矩阵进行去模糊化,形成最终的判断矩阵。 4) 正反性调整 去模糊后的判断矩阵不为互反矩阵,即aij×aji≠1,不便与后期进行一致性检验。因此,根据公式(10)对其进行互反性调整: (10) 5) 计算指标权重 针对正反性调整之后的判断矩阵,利用Matlab计算得到其最大特征值λmax是64.252,对应的特征向量就是相应指标的相对权重向量,即 W=(0.109 5 0.110 5 0.162 9 0.129 1 0.120 0 0.164 6 0.134 0 0.114 6 0.147 8 0.132 3 0.162 1 0.162 7 0.131 9 0.149 5 0.129 2 0.126 3 0.107 9 0.117 7 0.166 2 0.114 8 0.108 7 0.116 7 0.110 5 0.104 2 0.089 2 0.091 9 0.102 7 0.131 6 0.128 4 0.078 8 0.059 6 0.069 1 0.142 2 0.120 6 0.104 4 0.117 1 0.111 4 0.103 5 0.131 9 0.102 5 0.076 8 0.070 7 0.080 5 0.131 8 0.054 7 0.183 4 0.171 8 0.137 8 0.169 2 0.125 4 0.102 5 0.151 0 0.113 1 0.111 0 0.139 7 0.137 7 0.165 0 0.123 8 0.132 5 0.126 1 0.099 2 0.118 5 0.102 7 0.153 2)T。 归一化处理得到W′=(0.014 3 0.014 3 0.021 2 0.016 4 0.015 5 0.020 9 0.017 3 0.014 4 0.018 5 0.016 9 0.020 9 0.020 6 0.016 9 0.018 8 0.016 4 0.015 6 0.014 1 0.014 6 0.020 9 0.014 8 0.013 9 0.015 0 0.014 3 0.013 5 0.011 8 0.012 2 0.013 7 0.016 7 0.016 1 0.010 2 0.007 6 0.008 5 0.018 3 0.015 3 0.013 8 0.014 8 0.014 2 0.013 4 0.016 9 0.013 5 0.009 9 0.009 0 0.010 4 0.016 8 0.006 8 0.023 2 0.021 6 0.017 7 0.021 8 0.015 6 0.013 5 0.019 5 0.014 8 0.014 1 0.018 1 0.017 7 0.021 4 0.016 1 0.017 3 0.016 2 0.013 0 0.015 3 0.013 3 0.019 7)T。 6) 一致性检验 由于客观事故的复杂性与人认识的多样性,在判断矩阵构造中,不可能使判断矩阵是完全一致性矩阵。但要求判断矩阵须有大体上的一致性,可用λmax-n之差来度量对完全一致性的偏离。因此,引入判断矩阵的一致性指标CI。 CI=(λmax-n)/(n-1) (11) 判断矩阵的一致性指标CI与同阶随机一致性指标RI之比,称为判断矩阵的一致性比例CR。 CR=CI/RI (12) 通常情况下,对于n≥3阶的判断矩阵,当CR≤0.1时,认为判断矩阵的一致性可接受;当CR>0.1时,说明判断矩阵偏离一致性程度过大,必须对判断矩阵做适当修正,使之具有满意的一致性为止。 由于模架工程施工安全技术指标高达64个,现有的平均随机一致性指标RI(目前常适用的判断矩阵阶数只有n=30)已不满足检验条件,因此,使用Matlab求解出1~75的RI[14],其中n=64阶的RI=1.717。 因此,对模架工程的施工安全技术指标的计算权重进行一致性检验。经计算得:CI=(λmax-64)/63=0.005,CR=CI/RI=0.002 9<0.1,说明判断矩阵具有满意的一致性[15],该权重分配是合理的。 现有指标划分方法及特点见表6。 从表6可知,现有指标等级划分方法在模架工程权重等价划分均具有一定的不适用性。为使模架工程施工安全技术指标等级划分结果更加具有科学性和实用性,以安全技术指标的权重平均值为基准,划定相应等级的权重区间,从而实现施工安全技术指标的等级划分。针对模架工程的施工安全技术指标权重进行等级划分,并与目前常用的2/3/5权重分割法及±1倍标准差划分方法的划分结要进行对比分析,具体划分依据见表7,划分结果见表8。 由表8可知,针对模架工程安全技术指标体系中的64个安全技术指标,其中38个安全技术指标在现有规范中规定了相应的重要性程度等级,将其分别与课题组提出的权重等级划分方法、2/3/5权重分割法及±1倍标准差划分法等3种权重等级划分法的划分结果对比,发现这3种权重等级划分结果与现有规范中权重等级吻合率分别为32%、21%、26%,本文提出的方法吻合率相对高一些。 表6 现有指标划分方法及特点 表7 权重等级划分 表8 模架工程安全技术指标等级划分及比对 表8(续) 表8(续) 同时,2/3/5权重分割法及±1倍标准差划分方法的划分结果与课题组提出的权重等级划分方法结果的吻合率分别为86%和61%。其中共同存在差异的是R9、W24、G3和G10等4个指标,这4个指标本文权重等级划分的结果为“Ⅰ”等级指标,除W24外的3个指标和现有规范等级相同,而其他2种方法的划分结果均为“Ⅱ”等级指标,再次说明了本文提出的权重等级划分方法的合理性。 因此,基于三角模糊数的层次分析法对安全技术指标进行等级划分,可避免传统划分方法中的主观因素影响,具有一定的合理性和适用性,同时该指标体系的建立有利于安全管理人员在施工过程中有效开展事故预防和管理工作,在施工中及时发现安全隐患,避免安全事故发生。 本文基于德尔菲法和三角模糊数的层次分析法,针对模架工程开展了施工安全技术指标体系的构建及指标等级划分研究,得出以下结论: 1) 通过对典型施工安全事故分析及安全规范调研分析,筛选出了64个模架工程安全技术指标,通过层次分析法,构建了基于“人-物-环-管”等多因素耦合的、定性与定量指标相结合的模架工程施工安全技术指标体系。 2) 基于三角模糊数的层次分析法,提出了各个安全技术指标的重要性权重值,并将其划分为Ⅰ、Ⅱ、Ⅲ三个等级,通过与现有规范中安全技术指标权重级别及现有目前常用的指标权重等价划分方法对比分析,验证了其合理性与适用性。 3) 模架工程施工安全技术指标体系有利于安全管理人员在施工过程中有效开展事故预防和管理工作,在施工中及时发现安全隐患,避免安全事故发生。

3.3 权重等级划分



4 结论

