盾构法隧道施工地表沉降的影响因素及其优化控制方法分析
姚添宝
(北京市勘察设计研究院有限公司,北京 100038)
1 引 言
自2008年北京奥运会的成功召开,伴随着国内经济的快速发展,北京、上海、广州等地轨道交通建设的步伐在不断加快。对于大城市来说,解决交通拥堵最好的方式就是发展地铁或轻轨交通。而在目前城市环境下,盾构法施工无疑是最为便捷、安全和高效的[1~4]。
2 盾构法的优缺点
相较于传统矿山法施工,盾构法主要有以下优势:①开挖和衬砌施工环境相对安全,工人劳动安全有保障;②盾构机的推进、出土、管片拼装等全过程可实现自动化作业,施工劳动强度低。③施工中不受季节、风雨等气候条件影响,施工噪音和扰动小;④地面沉降控制好,邻近穿越重要风险对象时,安全性较高;⑤在松软含水地层中修建埋深较大的长隧道往往具有技术和经济方面的优越性。
伴随着大型化、机械化、自动化的特质,盾构法也有其不可规避的缺点:①设备制造维护成本高昂,不适合规模较小的工程;②设备本身具有针对性,适应环境的能力较差;③无法适用于断面有变化的情况;④对施工场地要求高,不适用于狭小、交通不便的场地。
3 盾构法施工地表沉降规律
通过对某地铁线路4处盾构区间的沉降监测数据对比分析发现,盾构通过后的地表沉降的发生可分为两个阶段,即盾尾脱出时和盾构脱出以后阶段。其中盾尾脱出瞬间产生的沉降量平均在总沉降量的90%以上,盾尾脱出以后产生的沉降量并不明显。由此可见,沉降产生的直接原因是盾构管片外间隙的地层损失未得到充分的填充,从而导致上部土体发生沉降[5~25]。
4 盾构法施工沉降控制研究
除上节提到的原因外,诸如盾构对地层的扰动、地层的工前状态等对地表沉降都有一定的影响,但这些因素普遍存在作用机理复杂,难以进行确定,所以此处拟通过数值方法对盾尾同步注浆参数进行分析,研究其与地表沉降的关系。
4.1 研究参数的确定
实际施工中控制盾尾同步注浆的参数主要有注浆压力、注浆量及浆液配比等。为便于进行数值分析,此处将注浆压力与注浆量近似转化为注浆加固的扩散范围,将浆液的配比近似转化为浆液加固体的强度。
由于加固体的强度仍涉及多方面的参数指标,为便于研究目标对象,此处先进强度参数的敏感性分析,确定主要因素,简化后续分析工作。
选取某工程进行底层简化,并忽略地下水等因素对工程的不利影响。模型采用位移约束条件,上表面不施加约束,底面三个方向全部施加约束,侧面采用水平单方向约束方式。采用FLAC3D建立三维数值计算模型,模型采用笛卡儿直角坐标系,x轴垂直盾构轴线,y轴与盾构轴线方向一致,z轴沿铅垂向上。
盾构隧道数值模型如图1所示,隧道开挖后地层位移情况如图2所示,围岩采用摩尔昆仑模型,盾构隧道管片采用弾性模型,管片厚度 0.3 m,均为实体单元,具体参数如表1、表2所示。

图1 数值计算模型 图2 隧道开挖后地层位移情况

围岩参数 表1

盾构管片参数 表2
综合考虑地层分布、围岩力学参数、隧道埋深等情况,选取第三层围岩的变形模量、横向变形系数(横向变形系数)、黏聚力、内摩擦角、抗拉强度五个因素作为实验对象,初步确定隧道的岩石力学参数的取值范围如表3所示。
对于所确定的5个研究因素,选择L25(56)正交表安排试验组合,设计5个试验研究参数在各自5种水平下的25种组合,具体实验方案如表4所示。

设定围岩参数取值范围 表3

正交试验安排表 表4
4.2 围岩参数敏感性分析
将按照正交实验设计表设计好的试验方案参数组合输入到数值模型中进行计算,在计算过程中监测预定断面隧道开挖后的位移情况,包括两隧道顶部、底部及上方地表共5处沉降变形情况,计算统计结果整理在表5中,并对结果数据进行极差分析,研究不同参数对隧道开挖后位移的影响程度的大小。

正交实验数值计算结果 表5
极差分析结果如图3~图5所示,从结果中可以看出,围岩参数对5个测点的位移影响规律基本一致,即变形模量E对位移的影响最大,其次是横向变形系数μ,其他3个因素黏聚力c、内摩擦角φ、抗拉强度t对围岩变形位移的影响是很小的。

图3 拱顶沉降极差分析 图4 拱底隆起极差分析 图5 地表中线沉降极差分析
由于三维数值模型计算时间长,拟采用回归公式反映不同参数组合下的位移变化。根据相关文献以及以上计算结果建议取如下的回归模型:

(1)
式中E、μ、c、φ、t分别为围岩的弹性模量、泊松比、黏聚力、内摩擦角、抗拉强度;m1~m7为回归系数。
采用式(1)的数学关系式拟合位移数据,通过“1stOpt15PRO”软件拟合数据得到位移与围岩参数间的数学关系式,回归系数如表6所示。

回归系数表 表6
4.3 盾构注浆参数敏感性分析
根据前述结论,确定以变形模量为盾尾注浆材料强度指标的主要研究参数,即数值计算分析中的主要控制因素为浆液的变形模量与浆液的扩散范围,参照相关工程资料及参考文献,可设定同步注浆浆液加固体的变形模量范围:50 MPa~200 MPa、注浆浆液扩散范围 0.3 m~0.6 m,按照两因素四水平正交设计表设计的实验方案如表7所示。

正交试验设计表 表7

正交试验计算结果 表8
将表7中的实验方案输入到数值计算模型中进行计算,将各组实验的计算结果按照各个导洞的顺序统计到表8中,并进行敏感性分析,统计结果如图6所示。
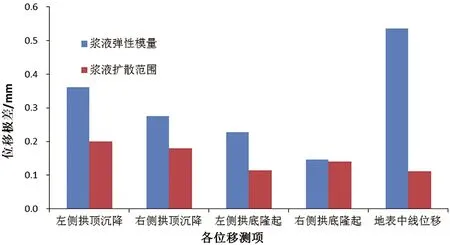
图6 敏感性分析
由图6可以发现,各部位变形对变形模量的敏感性强于浆液扩散范围,尤其是地表的变形。由此可得出以下结论,在相同外部条件下,通过调整注浆浆液强度参数,更容易实现对沉降变形的控制。
4.4 建立盾构注浆参数优化的数学模型
为寻找经济性最优的注浆参数组合,拟建立一个简单易行的注浆参数优化的数学模型。首先选取注浆浆液加固体的变形模量、注浆浆液扩散范围两个参数作为对盾构隧道工程施工经济性进行优化的变量,并分别以x1、x2来表示两个变量,即可把待优化问题的变量表示为X={x1,x2}。
然后建立优化变量与经济性之间的函数关系即目标函数,通过约束变量的取值到达对隧道工程施工经济性的优化。通过查阅相关资料与参考工程图纸,拟确定采用下式作为隧道施工锚固参数优化的目标函数(盾构外径 6.28 m,管片外径 6.00 m)。
构造函数如下式所示:
f(X)=(a+bx1)*(1.2*π*((x2+3)2-32))
(2)
式中:a—单位体积浆液的基础造价,取a=50元/m3;
b—由变形模量决定的浆液价格浮动系数,取b=10元/MPa;
假定待优化参数的取值范围:注浆浆液加固体的变形模量范围:50 MPa~200 MPa、注浆浆液扩散范围:0.3 m~0.6 m。
为求解函数,此处根据工程设计要求,引入隧道顶部沉降小于 15 mm、地表沉降小于 30 mm,作为安全性的约束条件,即:
g1(X)≤15,g2(X)≤30
(3)
确定了优化变量、同时给出目标函数及约束条件后便可构造一个优化数学模型,即在满足约束条件和下,求目标函数f(X)达到最小值时,设计变量X={x1,x2}的值。
那么需要优化的数学模型可表示成如下式形式:
minf(X)
s.tg1(X)≤15
g2(X)≤30
(4)
式中,min—表示取最小值;
s.t—表示满足的约束条件;
X—表示设计变量矩阵;
g1(X),g2(X)—表示变形约束条件。
4.5 求解经济性最优注浆参数
通过优化算法进行优化计算,得到优化后经济性最优的注浆参数:注浆浆液加固体的变形模量为 65.314 2 MPa、注浆浆液扩散范围为 0.573 5 m。
把经过优化计算得到的注浆参数组合代入到数值计算模型中进行计算,求解相应的变形量,将计算结果和原设计得到的计算结果进行对比分析如表9所示,可以看出优化后支护参数组合比原设计成本降低了13.05%,这基本证明了利用优化算法进行盾构法施工注浆参数造价优化方法的可行性,在完善成本函数、引入更加符合实际生产要求的控制条件后,可为施工成本控制提供一定的参考。

成本对比表 表9
5 结 论
盾构法隧道施工,地表沉降的主要影响因素是同步注浆的质量,在相同条件下对沉降进行控制的最便捷有效的手段就是调整注浆参数;
地表沉降对浆液强度参数更敏感,在满足填充地层损失所需基本注浆量的前提下,通过提升浆液强度参数对控制地表沉降更有效;
通过智能算法求解简化的注浆成本函数寻找最优解的方法基本可行,在完善成本函数、引入更加符合实际生产要求的控制条件后,可为控制施工成本提供一定的参考。

